Output Feedback Control for a Class of Nonlinear

Delayed Systems

Estelle Cherrier

, Tarek Ahmed-Ali

, Mondher Farza

, Mohammed M’Saad

and Franc¸oise Lamnabhi-Lagarrigue

GREYC UMR 6072 CNRS

Boulevard du Mar´echal Juin 14050 Caen, France

L2S UMR 8506 CNRS Sup´elec

3 rue Joliot-Curie 91192 Gif-sur-Yvette, France

Abstract. In this work, delays affecting either the output measurements or the

input for a class of nonlinear systems are coped with. This problem is particulary

challenging since time delays arise in variety of applications, such as systems

communicating through (wireless) networks. Indeed when the controller is a re-

mote one, delays must be taken into account, affecting both the input and the

output of the system. We ﬁrst present a set of cascade high gain observers for

triangular nonlinear systems with delayed output measurement. A sufﬁcient con-

dition ensuring the exponential convergence of the observation error towards zero

is given. This approach is then applied to design an output feedback control in the

presence of input delay. These results are illustrated through numerical simula-

tions.

1 Introduction

Systems communicating through wireless network are now quite common. Data trans-

missions such as output measurements or control laws are necessarily subject to delays

inherent to the communication process. The aim of this paper is twofold. Delays af-

fecting either the output measurements or the input for a class of nonlinear systems are

coped with. This problem is particulary challenging since time delays affecting input

or output measurements arise in a variety of applications. One can cite for example

systems which are controlled by a remote controller. In these systems, the input or the

output data are transmitted between the controller and the system throughout a commu-

nication system, which can be a wireless network. This network introduces a time-delay

between the process and the controller. The design of controllers for such systems can

be viewed as an output feedback design based on state prediction system. In the linear

case, this problem has been solved by the well-known Smith predictor [1] and several

predictive control algorithms [2], [3]. Recently, for the nonlinear case, a new kind of

chained observers which reconstruct the state at different delayed time instants for drift

observable systems has been presented in [4]. The authors showed, by using Gron-

wall lemma, that under some conditions on the delay, exponential convergence of the

Cherrier E., Ahmed-Ali T., Farza M., M’Saad M. and Lamnabhi-Lagarrigue F. (2009).

Output Feedback Control for a Class of Nonlinear Delayed Systems.

In Proceedings of the International Workshop on Networked embedded and control system technologies: European and Russian R&D cooperation,

pages 45-55

 SciTePress

chained observers is ensured. These conditions have been relaxed in [5] by using an ap-

proach based on a ﬁrst-order singular partial differential equation. On the other hand, in

[6] a novel predictor for linear and nonlinear systems with time delay measurement has

been designed. This predictor is a set of cascade observers. Sufﬁcient conditions based

on linear matrix inequalities are derived to guarantee the asymptotic convergence of

this predictor. Concerning delays affecting the input of the system, very little attention

has been paid to this subject. For relevant work, the reader is referred to [7] and the

references therein.

In the present work, the design of nonlinear observers in the presence of delayed

output measurement is ﬁrst dealt with. To this purpose, we design a set of cascade high

gain observers for nonlinear triangular systems by considering a time delay in the out-

put measurement. We will show that the general high gain observer design framework

developed in [8], [9], [10], to mention a few, for delay-free output measurements can

be extended to systems with delayed output. More precisely, we propose to use a suit-

able Lyapunov-Krasovskii functional and a sufﬁcient number of high gain observers, in

order to guarantee the exponential convergence of the estimated state at time t towards

the true state at time t, even if the output is affected by any constant and known delay.

We will also give an explicit relation between the number of observers and the delay.

Then in a second part, this observer is used to design a feedback controller based on a

dual approach of high gain techniques [11].

The present paper is organized as follows : In section 2, we present the class of con-

sidered systems and the different assumptions. In the third one, we present the proposed

observers and prove their convergence. Section 4 is devoted to the design of a feedback

control law based on the previous observers. In the last section, we illustrate our results

throughout simulations on academic examples.

2 Preliminaries and Notations

First some mathematical notations which will be used throughout the paper are intro-

duced.

The euclidian norm on R

will be denoted by ||.||. The matrix X

represents the

transposed matrix of X. e

(i) = (0, . . . , 0,

z}|{

1 , 0, . . . , 0)

| {z }

s components

∈ R

, s ≥ 1 is the i

vector of canonical basis of R

. The convex hull of {x, y} is denoted as Co(x, y) =

{λx + (1 − λ)y, 0 ≤ λ ≤ 1}. λ

min

(S) and λ

max

(S) are the minimum and maximum

eigenvalues of the square matrix S.

In the ﬁrst part of this paper, we consider the following class of nonlinear systems:

˙x = Ax + φ(x, u)

y = Cx(t − τ ) (1)

where

A =







0 1 0 . . . 0

0 0 1 0

. 0 . . . 1 0

. . . . . . . 1

0 . . . . . . . . . 0







(2)

C =



1 0 . . . 0



(3)

φ(x, u) =







(x, u)







(4)

The term τ represents the measurement time delay, x(t) ∈ R

is the vector state

which is supposed unavailable. The output y(t) ∈ R is a linear function of the state

x at time t − τ . The input u ∈ U where U is a compact set in R. The functions

, i = 1, . . . , n are supposed smooth. This class represents the class of uniformly

observable systems. It has been shown [8], [9] that these models concern a wide variety

of systems, such as bioreactors...

Throughout the paper, we assume that the following hypotheses are satisﬁed.

H1. The functions φ

(x, u) are triangular in x, i.e

∂φ

(x,u)

∂x

k+1

= 0, for k = i, . . . , n − 1

H2. The functions φ

(x, u) are globally Lipschitz, uniformly in u

H3. The time delay τ is supposed constant and known.

3 Observer Design

In this section, we consider an arbitrary long time delay τ affecting the output mea-

surement of system (1). The proposed nonlinear observer for system (1) is a set of m

cascade high gain observers. Each one of them estimates a delayed state vector with

sufﬁciently small delay

In order to present the proposed observer, we use the following convenient notations

adopted from [4]:

(t) = x(t − τ + j

)

where j = 1, . . . , m

Then the proposed observer can be written in the following form, for j = 1, . . . , m:

ˆx

= Aˆx

+ φ(ˆx

) − θ∆

−1

′

C(ˆx

(t −

) − x(t − τ ))

ˆy

= C ˆx

(t −

)

. =

ˆx

= Aˆx

+ φ(ˆx

) − θ∆

−1

′

C(ˆx

(t −

) − ˆx

j−1

(t))

ˆy

= C ˆx

(t −

) = C ˆx

j−1

(t) (5)

where θ is a positive constant satisfying θ > 1.

S is a symmetric positive deﬁnite matrix, solution of the following algebraic Lya-

punov equation:

SA + A

S − C

C = −S (6)

and ∆ is a diagonal matrix which has the following form :

∆ = Diag



1, . . . ,

i−1

, . . . ,

n−1



. (7)

We will show that the vector ˆx

(t) estimates the delayed state x

(t), j = 1, . . . , m −1

and ˆx

(t) estimates x(t).

Before proving the exponential convergence of the proposed chained observers, we

consider the case when the delay τ is sufﬁciently small. Then only one high gain ob-

server is required to estimate the state of system (1).

Lemma 1. Consider the following observer:

ˆx = Aˆx + φ(ˆx, u) − θ∆

−1

C(ˆx(t − τ ) − x(t − τ ))

ˆy = C ˆx(t − τ ) (8)

Then for sufﬁciently large positive θ, there exists a sufﬁciently small positive constant

such that ∀τ ≤ τ

, observer (8) converges exponentially towards system (1).

Proof

First let us denote the observation error as ˜x = ˆx − x.

Then we will have:

˜x = A˜x + φ(ˆx, u) − φ(x, u) − θ∆

−1

C ˜x(t − τ ) (9)

If we apply the relation

˜x(t) = ˜x(t − τ ) +

t−τ

˜x(s)ds (10)

and the change of coordinates ¯x = ∆˜x, system (9) can be rewritten in the following

manner:

¯x = θ(A − S

−1

C)¯x + ∆(φ(ˆx, u) − φ(x, u)) + θS

−1

′

t−τ

¯x(s)ds. (11)

In order to derive an upper bound τ

for the delay τ, to ensure the exponential con-

vergence to zero of the error ¯x, we use the following Lyapunov-Krasovskii functional

[12]:

W = ¯x

S ¯x +

t−τ

¯x(ξ)||

dξds. (12)

This functional can be written after an integration by parts as follows (see [12] for more

details):

W = ¯x

S ¯x +

t−τ

(s − t + τ

)||

¯x(s)||

ds (13)

If we compute its time derivative, we obtain

W ≤ θ¯x

S + SA − 2C

C)¯x + 2¯x

S∆(φ (ˆx) − φ(x))

+2θ¯x

t−τ

¯x(s)ds + τ

¯x(t)||

−

t−τ

¯x(s)||

ds (14)

Using (6), we have

W ≤ −θ¯x

S ¯x + 2¯x

S∆(φ (ˆx) − φ(x)) + −θ¯x

C ¯x + 2θ¯x

t−τ

¯x(s)ds

+ τ

¯x(t)||

−

t−τ

¯x(s)||

ds. (15)

Note that by using the mean value theorem [13], we can write

∆ (φ(ˆx) − φ(x)) = ∆

n,n

i,j=1

(i)

(j)

∂φ

∂x

(ξ)

∆

−1

¯x (16)

where ξ ∈ Cov(x, ˆx).

Then we will have

2¯x

S∆(φ (ˆx) − φ(x)) = 2¯x

S∆(

n,n

i,j=1

(i)

(j)

∂φ

∂x

)∆

−1

¯x (17)

Using the triangular structure and the Lipschitz properties of the functions φ

, and the

fact that θ > 1, we deduce that

||2¯x

S∆(φ (ˆx) − φ(x))|| ≤ k

V (18)

where V = ¯x

S ¯x and k

is a positive constant which does not depend on θ.

Using the following property :

2θ¯x

t−τ

¯x(s)ds − θ¯x

C ¯x

= −θ(Cx + C

t−τ

¯x(s)ds)

(Cx + C

t−τ

¯x(s)ds)

+ θ(

t−τ

¯x(s)ds)

t−τ

¯x(s)ds). (19)

This means that

2θ¯x

t−τ

¯x(s)ds − θ¯x

C ¯x ≤ θ(

t−τ

¯x(s)ds)

t−τ

¯x(s)ds) (20)

From this, we will have

W ≤ −θV + k

V + θ(

t−τ

¯x(s)ds)

t−τ

¯x(s)ds)

+τ

¯x(t)||

−

t−τ

¯x(s)||

ds (21)

Now, let us remark that if we use equation (11), it comes:

¯x(t)||

≤ θ

[V + ||

t−τ

¯x(s)ds||

] (22)

where k

is also a positive constant which does not depend on θ.

Using this and equation (21), we will have:

W ≤ −θV + k

V + θI

CI + τ

[V + ||I||

] −

t−τ

¯x(s)||

ds. (23)

where I =

t−τ

¯x(s)ds.

To prove the above lemma (1), it is sufﬁcient to ﬁnd conditions which guarantee the

inequality

W +

√

W < 0.

From (23), we can write

W +

√

W ≤ −θV + k

V +

√

+ θI

CI + τ

[V + ||I||

]

√

t−τ

¯x(s)||

ds −

t−τ

¯x(s)||

ds. (24)

If we use the following Jensen’s inequality :

t−τ

¯x(s)||

ds ≥

||I||

(25)

and if τ

≤

√

θ, we have

W +

√

W ≤ −(θ − k

− τ

−

√

)V − (

− θ − τ

−

√

)||I||

(26)

Then, we can say that lemma 1 is veriﬁed for











θ ≥ max{2, (k

+ k

√

)}

(27)

To summarize Lemma 1, it gives the maximum delay supported by observer (8) which

enables ˆx(t) → x(t), once θ has been ﬁxed according to conditions (27). To cope with

a larger measurement delay, we propose in next paragraph a procedure to estimate x(t),

based on a chain of high-gain observers: each observer will estimate the state at a given

fraction of the output delay.

Cascade High Gain Observers. After proving that the convergence of the observer (8)

requires a small delay, we will see that when the delay is arbitrary long, a set containing

a sufﬁcient number of cascade high gain observers (5) can reconstruct the states of

system (1).

Theorem 1. Let us consider system (1), then for any constant and known delay τ, there

exist a sufﬁciently large positive constant θ and an integer m such that the observer (5)

converges exponentially towards the system (1).

Proof

The convergence of the cascade observer will be proved step by step :

Step 1: We consider the ﬁrst observer in the chain:

ˆx

= Aˆx

+ φ(ˆx

) − θ∆

−1

C(ˆx

(t −

) − x(t − τ ))

ˆy

= C ˆx

(t −

) (28)

We remark that x(t − τ) = x

(t −

) and consequently, if we choose θ sufﬁciently

large, and by choosing the integer m such that m ≥ θ

τ, then ˆx

(t) converges towards

(t) = x(t − τ +

) = x(t − (m − 1)

Indeed, we are brought back to conditions of Lemma 1, since the delay to handle with

is now

, which is assumed smaller than

Step j: at each step (j = 2, . . . , m), we estimate the delayed state x(t − τ + j

)

by using the following observer:

ˆx

= Aˆx

+ φ(ˆx

) − θ∆

−1

C(ˆx

(t −

) − ˆx

j−1

(t))

ˆy

= C ˆx

(t −

) = C ˆx

j−1

(t) (29)

It is not difﬁcult to see that by considering the observation error vector ˜x

= x

− ˆx

if we add and subtract the term θ∆

−1

j−1

(t) in the previous equation, we

obtain

˜x

= A˜x

+ φ(ˆx

) − φ(x

) − θ∆

−1

C(˜x

(t −

) − ˜x

j−1

(t)) (30)

If we consider the following change of coordinates ¯x

= ∆˜x

, we will have

¯x

= θ(A − S

−1

C)¯x

+ ∆(φ(ˆx

) − φ(x

))

+ θS

−1

t−

¯x

(s)ds − θS

−1

C ¯x

j−1

. (31)

In order to prove by recurrence the convergence of the error ¯x

, we suppose that the

observation error ¯x

j−1

(t) converges exponentially towards zero.

Then we consider the following Lyapunov-Krasovskii functional

= ¯x

S ¯x

t−

(s − t +

)||

¯x

(s)||

ds (32)

Then its time derivative satisﬁes the following inequality:

≤ −θ¯x

S ¯x

+ 2¯x

S∆(φ (ˆx

) − φ(x

)) + −θ¯x

C ¯x

− 2θ¯x

C ¯x

j−1

+2θ¯x

t−τ

¯x

(s)ds + τ

¯x

−

t−τ

¯x

(s)||

ds. (33)

As in the proof of the lemma 1, we will also have:

≤ −(θ − k

′

+ θI

− 2θ ¯x

C ¯x

j−1

+ τ

¯x

−

t−τ

¯x

(s)||

ds (34)

where V

= ¯x

S ¯x

, I

t−τ

¯x

(s)ds and k

′

is a positive constant which does not

depend on θ and k

′

≥ k

Now, by using Young’s inequality, we derive the following inequalities

¯x

≤ τ

′

+ ||I

+ ||¯x

j−1

) (35)

−2θ¯x

C ¯x

j−1

≤

√

min

(S)

||¯x

j−1

. (36)

where k

′

is a positive constant which does not depend on θ and k

′

≥ k

Choosing τ

, and using (34), (35) and (36), we derive

√

≤ −(θ − k

′

− τ

′

−

√

− (

− θ − τ

′

−

√

)||I

√

min

(S)

+ k

′

)||¯x

j−1

(37)

Then, we can say that if



θ ≥ 2 + k

′

+ k

′

, τ

(38)

we will have

≤ −

√

+ (

√

min

(S)

+ k

′

)||¯x

j−1

(39)

Using the comparison lemma [14], we conclude that if ¯x

j−1

converges exponentially

towards zero, then ¯x

converges also exponentially towards zero. Note that conditions

(38), also ensure the convergence of the ﬁrst observer (j = 1), then we deduce, recur-

sively, that all observation errors converge exponentially towards zero.

4 Output Feedback Controller Design

In previous section, we addressed an observer synthesis issue, when the output mea-

surement is affected by any delay. Now we consider what can be thought of as a dual

problem. The aim is to design a stabilizing feedback control law when the controller

is a remote one, which inevitably leads to delays on the system input. To this end we

consider the following class of nonlinear systems:



˙x(t) = Ax(t) + φ( x(t)) + bu(t − τ )

y(t) = Cx(t)

(40)

and we assume that hypotheses H

to H

are fulﬁlled.

We detail now a solution to the above problem that makes use of the previous results.

In order to cope with the input delay, we use the above cascaded observer (5) to derive

a prediction of state x(t) used in the feedback control u(t − τ). For sake of simplicity,

we suppose that we need only one observer to face this delay. The same reasoning as in

previous section can be extended to deal with a larger delay, with cascaded observers.

Using the work developed in [11], the feedback control which stabilizes (40) can be

expressed as:

u(t) = −λ

S∆

ˆx(t + τ ) (41)

where λ > 0 is a suitable tuning parameter like the parameter θ in the observer design

and the matrix ∆

is deﬁned as in (7) where θ is replaced by λ.

Using the results detailed in previous section, ˆx(t + τ) can be computed, see (5).

Then this predicted state is used to compute eq. (41). As a consequence, this prediction

cancels the effects of the delay affecting the transmission of the control law.

We give now a sketch of how to proceed. • Make the following variable change

to obtain an estimation of the predicted state: z(t) = ˆx(t + τ ). This is equivalent to

ˆx(t) = z(t − τ).

Then the observer can be expressed as:

˙z(t) = Az(t) + φ(z(t)) + bu(t) − θ∆

−1

(y(t) − z(t − τ ))

(42)

where u(t) = −λ

S∆

z(t).

We are now brought back to the former problem of section 3. • The key point is to use

the delayed control law u(t −τ) in the system dynamics, which corresponds to the real

applied control, whereas we use u(t) in the observer’s dynamics.

•The reader is referred to [11] for a detailed proof of the stabilization of the system (40)

and the convergence of the observer (42).

5 Example

To illustrate the obtained results, consider the following nonlinear system, affected ﬁrst

only by delayed measurements:







˙x

(t) = x

(t)

˙x

(t) = −2x

(t) + 0.5 tanh ( x

(t) + x

(t)) + x

(t)u(t)

y(t) = x

(t − τ )

(43)

The input is u(t) = 0.1 sin(0.1t). System (43) belongs to the considered class of

triangular systems with Lipschitz nonlinearities (1).

The initial conditions for the system and for the observer have been chosen as x(t) =



1 −1



, ˆx(t) =



0 0



, ∀t ∈ [−τ, 0].

Simulations have been performed using Matlab-Simulink, and a fourth order Runge-

Kutta integration routine. The high gain parameter is set to θ = 2, the control parameter

is set to λ = 2. We show the efﬁciency of the stabilizing control law given in eq. (40)

and (41), based on observer (42), on the example below:







˙x

(t) = x

(t)

˙x

(t) = −2x

(t) + 0.5 tanh ( x

(t) + x

(t)) + u(t − τ )

y(t) = x

(t)

(44)

The stabilization of the controlled state to zero is shown in ﬁgure 1.

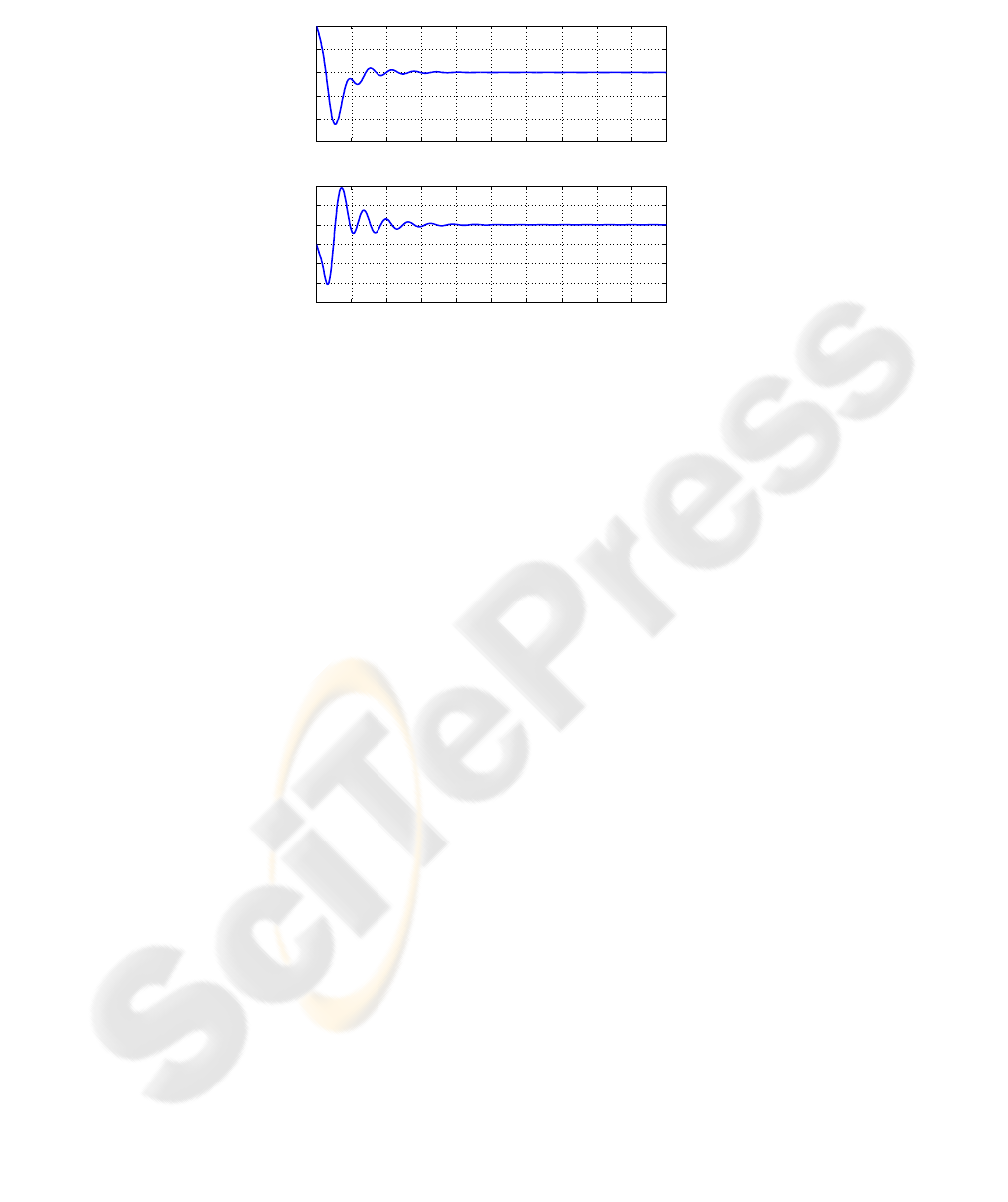
0 2 4 6 8 10 12 14 16 18 20

−1.5

−1

−0.5

0.5

State x

Time (s)

0 2 4 6 8 10 12 14 16 18 20

−4

−3

−2

−1

State x

Time (s)

Fig.1. Evolution of the controlled states.

6 Conclusions

In this paper, a novel predictor based on high gain observer has been presented. This

observer can be applied to the class of nonlinear uniformly observable systems, subject

to input or output delays arising from communication networks for example. The case

of a variable delay can be considered on the basis of the presented work. The design of

adaptiveobservers for nonlinear systems with delayed output and uncertain or unknown

parameters is under investigation.

References

1. Smith, O.: Closer control of loops with dead-time. Chem. Eng. Prog. 53 (1957) 217–219

2. Clarke, D., Mohtadi, C., Tuffs, P.: Generalized predictive control-part I and II. Automatica

23 (1987) 137–160

3. Shaked, U., Yaesh, I.: H-inﬁnity static output-feedback control of linear continuous-time

systems with delay. IEEE Trans. Automatic Control 43 (1998) 1431–1436

4. Germani, A., Manes, C., Pepe, P.: A new approach to state observation of nonlinear systems

with delayed output. IEEE Trans. Automatic Control 47 (2002) 96–101

5. Kazantzis, N., Wright, R.: Nonlinear observer design in the presence of delayed output

measurements. Sys. & Control Letters 54 (2005) 877–886

6. Besanc¸on, G., Georges, D., Benayache, Z.: Asymptotic state prediction for continous-time

systems with delayed input and application to control. In: Proceedings of the European

Control Conference, Kos, Greece. (2007)

7. Mazenc, F., Bliman, P.: Backstepping design for time-delay nonlinear systems. IEEE Trans.

Automatic Control 51 (2006) 149– 154

8. Bornard, G., Hammouri, H.: A high gain observer for a class of uniformly observable sys-

tems. In: Proceedings of the 30th IEEE Conference on Decision and Control, Brighton,

England. (1991)

9. Gauthier, J., Hammouri, H., Othman, S.: A simple obsever for nonlinear systems: Applica-

tion to bioreactors. IEEE Trans. Automatic Control 37 (1992) 875–880

10. Hammouri, H., Farza, M.: Nonlinear observers for locally uniformly observable systems.

ESAIM J. on Control, Optimisation and Calculus of Variations 9 (2003) 353–370

11. Maˆatoug, T., Farza, M., M’Saad, M., Kouba, Y., Kamoun, M.: Adaptive output feedback

controller for a class of uncertain nonlinear systems. In: Proceedings 17th IFAC World

Congress, Seoul, Korea. (2008)

12. Fridman, E.: New LyapunovKrasovskii functionals for stability of linear retarded and neutral

type systems. Sys. & Control Letters 43 (2001) 309–319

13. Zemouche, A., Boutayeb, M., Bara, G.I.: Observer design for nonlinear systems : An ap-

proach based on the differential mean value theorem. In: Proceedings of the Joint 44th

IEEE Conference on Decision and Control and European Control Conference, Seville, Spain.

(2005)

14. Khalil, H.: Nonlinear Systems. Prentice Hall (2002)