Stability and Performance of Scheduling Policies

in a Transportation Node

Mauro Boccadoro

, Francesco Martinelli

and Paolo Valigi

DIEI, University of Perugia, Italy

DISP, University of Rome ”Tor Vergata”, Italy

Abstract. In this paper we consider the dynamic model of a logistic node of a

transportation network and study dispatching feedback policies in terms of sta-

bility and optimality. A necessary and sufﬁcient condition for the existence of a

stable feedback policy is given and a policy is presented which would be optimal

if the transportation resources were continuous.

1 Introduction

An intermodal logistic system can be modeled as a network comprising a set of nodes

(hubs and terminals) connected by the links established by the transport operations,

which, in general, take place under different modes. The management of logistic nodes

in this network is a complex problem where several factors have to be taken into ac-

count, from the availability of carriers and their assignment to particular tasks (in terms

of products to be shipped, destinations or routes), and fulﬁllment of various perfor-

mance criteria such as timely delivery, minimization of transportation and inventory

costs (possibly, both at the logistic nodes and at the destinations); see among others,

[1–4].

Many instances of decisional problems for these systems are presented and solved

in the literature; often transportation problems can be addressed in terms of linear pro-

gramming problems, see e.g., [5–8], and developing ad-hoc techniques to obtain the

solutions, such as dynamic programming with linear approximation of the (unknown)

value function. It is worth mentioning that by the approach of [5, 6] the framework of

the Logistic Queuing Networks is introduced.

A slightly different paradigm considers shipping policies for simpliﬁed models of a

logistic network (or a part of it) and addresses the minimization of transportation and

inventory costs, see for example [9,10] and [15] where a stochastic setting is adopted.

Still another example of management problems for a logistic node is represented by the

optimization of space allocated for containers in ports (e.g., [13]); or the optimization

of the operations of discharging containers from a ship, their location in the terminal

yard and the upload of new containers [14]. In these last two cases, the performances

considered can be also viewed in terms of the necessity to maintain low levelsof stocked

products in the logistic node (in this case, a port). The stability of the dynamics of the

stock at a logistic node is therefore a relevant issue to be taken into account.

Boccadoro M., Martinelli F. and Valigi P. (2009).

Stability and Performance of Scheduling Policies in a Transportation Node.

In Proceedings of the 3rd International Workshop on Intelligent Vehicle Controls & Intelligent Transportation Systems, pages 86-95

 SciTePress

In order to study the stability (and the performance of stabilizing policies) from

a dynamical point of view, in this paper a simpliﬁed model of a logistic node in a

transportation network is considered and feedback policies based on the current state

of the system are deﬁned to control the node. The scenario is similar to those arising in

other applicative domains (like in manufacturing, communications, computer systems

or queuing networks in general), so the feedback policies considered in this paper have

been inspired by various well established techniques developed in those domains. The

stability of these policies will be investigated and a necessary and sufﬁcient condition

for the possibility of stabilizing the system will be determined. The sufﬁciency will be

established in a constructive way by determining a class of policies which guarantee the

stability of the system. A comparison among the performances of different stabilizing

policies will be carried out through simulations, showing that a policy, inspired by a

control known as optimal for the ﬂuid version of the problem, will provide the best

results among the policies considered in the paper.

2 Problem Formulation

Consider the discrete time model of a logistic node collecting Q different types of wares

which have to be shipped to P different locations, and let x

(k) ≥ 0 be the quantity of

items of type j = 1, . . . , Q, with destination i = 1, . . . , P , stocked at the logistic node

at time t

, and collected in the buffer

. In this model a destination could be more

in general considered as a route among different locations, established through some

routing algorithm.

The time evolution of each x

is observed at various decisional time instants t

and as such characterized by a discrete time dynamics. Denoting d

(k) the amount of

goods of type j to be sent to destination i arriving in the node in the interval (t

, t

k+1

)

and u

(k) the amount of goods of type j shipped to destination i from the node in the

same interval (t

, t

k+1

), we have:

(k + 1 ) = x

(k) + d

(k) − u

(k) (1)

In addition to this dynamics, we consider that of the vehicles executing the shipping

task. Let n

(k) be the number of vehicles assigned to destination i in the interval

, t

k+1

); the total number N (k) of vehicles present in the node at time t

obeys to the

following equation:

N(k + 1) = N(k) + R(k) −

i=1

(k) (2)

where R(k) is the number of vehicles arriving from outside in the interval (t

, t

k+1

Notice that, according to the above dynamics, the total number of vehicles available for

a shipping task at time t

is given by

These buffers could be considered as virtual, in the sense that in some cases we may have

items which are physically stocked in different places according to their type (in such a way

that the physical content of a buffer is given by

i=1

) as it happens for the stocked ﬁnished

products in a factory.

(k) := N (k) + R(k) (3)

To model the inﬂow of vehicles R(k), ﬁrst consider the simple scenario where there is

a ﬁxed quantity N

of vehicles which could serve the logistic node (as if for example,

the logistic node is a shipper who owns a certain quantity N

of trucks). A traveling

time T

∈ N is associated to each route (i.e. destination) i; in particular T

denotes the

round-trip time, i.e. the interval after which a vehicle is again available at the node after

completion of a shipping task to destination i. In this case R(k) =

i=1

(k − T

)

is the number of vehicles coming back from their expedition, and therefore (2) reads as

follows:

N(k + 1) = N(k) +

i=1

(k − T

) −

i=1

(k); N(0) = N

(4)

Notice that the total sum of vehicles (those at the logistic node and those traveling)

equals N

at each time instant.

In other cases we can consider the logistic node and the shippers as separate entities,

so that the total number of vehicles which are going to access the logistic node varies

with time; in such situations N

can be obtained through a suitable average of the expe-

dition history in the node, and can be possibly perturbed when new vehicles are assigned

to (or removed from) the node. A possible way to model this situation is by perturbing

the signal R(k), i.e., R(k) =

i=1

(k − T

) + ∆(k), where ∆ is a disturbance signal

characterized by certain statistical properties (e.g. zero mean). Another interesting ex-

tension would be to add to the round trip time some noise (possibly asymmetric, in the

sense that positive perturbations, so that

> T

, are more likely to occur than negative

ones). As a ﬁrst approach to the problem, in the following we consider the simpliﬁed

model (4), i.e., assuming that the T

’s are deterministic quantities and N

is ﬁxed. In this

case the number of available vehicles at time t

is: N

(k) = N (k) +

i=1

(k − T

Let’s now consider the interaction between the stock dynamics (1) and the vehicle

dynamics (4). To this end, assume that each vehicle has identical volume capacity and

that each item of type j = 1, . . . , Q has a relative volume with respect to vehicle

capacity v

≤ 1 (that is, a vehicle has unit capacity). Accordingly,we havethe following

constraint for any route i:q

j=1

(k) ∈ [0 , n

(k)]. (5)

Since n

(k) vehicles are used at time t

for route i, it is reasonable that the above

quantity is larger than n

(k) − 1 (actually, by the policies that will be considered in this

paper, vehicles travel completely loaded).

The objectives of this work will be essentially two. First, derive conditions on the

stability of the system, that is conditions on the inﬂow process d(·), (relative) part vol-

umes v

, traveling times T

and number of vehicles N

such that there exists a policy of

selection of n

(·) and u

(·) which maintains limited all the buffers x

(·). Second, ana-

lyze the performance of some class of policies, trying to solve the optimization problem

consisting in the selection of the n

(k) and of the u

(k) to minimize:

J =

k=1

g[x(k)]γ

(6)

where γ ∈ (0, 1] is a discount factor and K a planning horizon, possibly inﬁnite. The

function g(·) penalizes waiting freights in the node, e.g., for a linear g(x),

g(x) =

i=1

j=1

(7)

We now make a ﬂuid approximation for the variables involved in (1), considering

, d

and u

as continuous quantities. Accordingly, the information about the vol-

ume of each type j = 1, . . . , Q is now carried by the continuous variables (now the

relative volumes v

have no sense per se, hence they will be dropped in the follow-

ing) and each cost c

, assuming a ﬁxed i, now has the meaning of holding cost of part

j = 1, . . . , Q per unit volume

. Notice that also the variables N, N

, n

will represent

volumes (multiples of the unit volume).

We will deal with the two problems above by restricting the control policies to those

which make vehicles travel completely full (this is possible under the ﬂuid approxima-

tion of the materials): this should represent, as remarked below, a correct choice under

heavy trafﬁc conditions. Notice, also, that transportation costs have not been included

in the cost index: this depends on the fact that (i) transportation costs are considered

constant in time; (ii) we restrict the analysis to policies which make all vehicles travel

completely full. The assumptions above imply that the transportation cost is a ﬁxed

component that does not inﬂuence the optimization problem. The choice of considering

the vehicles fully loaded is reasonable under heavy trafﬁc conditions (where allowing

the possibility of sending partially full vehicles may even compromise the stability), but

may become signiﬁcantly sub-optimal in the case of reduced inﬂow rates, large holding

costs c

and small traveling costs.

3 Stability

As an introduction, consider a one part-type system (Q = 1) with constant inﬂow

processes d

and equal transportation times T

= T , ∀i. The equations are then:

(k + 1) = x

(k) + d

− u

(k), i = 1, . . . , P (8)

(k) ∈ [0, n

(k)] (9)

i=1

(k) ≤ N

(k) (10)

N(k + 1) = N(k) +

i=1

(k − T ) −

i=1

(k) (11)

Formally, as if the system were described by new variables x

′

= x

(and similarly for d

and u

) and c

′

= c

; dropping the “prime” and remaining with the same notation.

Based on the Little’s law, the necessary and sufﬁcient condition of stability for this

system should be:

i=1

≤

(12)

In fact, N

/T is actually the effective number of vehicles available at each time unit,

and hence also the volume of goods the node may handle in each unit of time. This must

be equal to the volume arriving from outside, i.e.

i=1

The stronger condition that there exists a static vehicle allocation such that:

T d

≤ n

(13)

for all i, which implies condition (12), actually is not necessary (but clearly sufﬁcient,

since if it holds, allows to apply a policy where vehicles are divided once for ever among

the tasks and each task is fulﬁlled, with no interaction among them), as shown in the

following simple example.

Example. Consider a system with d

= d

= .5, T = 1, N

= 1. Clearly it is

not possible to distribute vehicles once for ever (in fact for any static selection of n

condition (13) does not hold). However (12) holds and, in fact, the periodic allocation

(·) = {1, 0, 1, . . .} and n

(k) = 1 − n

(k), maintains the buffers bounded. 

Let us now return to the general case, but considering at ﬁrst a constant inﬂow

process. Condition (12) should be substituted by:

i=1

j=1

≤ N

(14)

which will be shown to be necessary and sufﬁcient for the stability of the node. In this

case, in fact, the quantity d

plays the role of a work inﬂow in the system per unit of

time (in the sense that for each item of type j to be sent to i, the system must allocate

a working capacity of T

, where the total working capacity is N

). In the case of time

varying inﬂow rates (but with the inﬂow rate oscillating in a bounded interval), the same

condition should hold with average inﬂow rates

Remark 1. Actually, while (14) is necessary for stability, the proof reported below only

holds if the inequality in (14) is strict. We believe however that also the equality ensures

the stability. Notice, in any case, that a strict inequality should be considered in practical

settings to guarantee a certain degree of robustness of the stability property.

The previous discussion can be formalized in the following theorem.

Theorem 1. Condition (14) is necessary and sufﬁcient (if taken with strict inequality)

to maintain all the buffers in the node bounded at all times.

Proof. Necessity. The necessity of (14) can be shown by relaxing the integer constraint

on the n

(k). If the vehicle resource is not discrete, it is possible to maintain all the

buffers bounded only if there exists a static assignment of the vehicles (notice in fact

that in our model the inﬂow process is constant) which balances the freight inﬂow into

the system for all the routes i. The freight inﬂow into the system of parts to be sent

on the route i is given by D

j=1

. If n

vehicles are assigned to this route,

since each transport requires T

time units, n

vehicles are available only every T

time

units. The amount of wares accumulated in such a period is given by D

. So it must

be D

≤ n

. Summing over i, we get the condition (14). Since this condition is

necessary for the relaxed problem, it is necessary also for the original problem.

Sufﬁciency. The proof of sufﬁciency is constructive: we exhibit a class of policies

which, if (14) holds with strict inequality, ensures that all the buffers remain bounded.

The proof is very similar to the proof of Theorem 1 in [11]. The class of policies ensur-

ing stability is like the CAF policies in [11] where, however, the buffer x

is processed

not until it is cleared (level zero) but until its level becomes lower than N

. That is: all

the vehicles are assigned to a single route by ﬁlling them with the products of a certain

buffer B

(selected according to the CAF rule (15) reported below) only if this buffer

has sufﬁcient stock to use all vehicles, and the buffer is changed when this is no more

possible. If no buffer can ﬁll all the vehicles, the system remains idle until this becomes

possible. Let τ

denote the time a buffer has been ﬁnished to be processed. At each time

the next buffer will be the one (denoted with a ∗) satisfying:

∗

(τ

) ≥ ǫ

i,j

(τ

) (15)

for some ǫ > 0 (e.g. the policy which selects the buffer with the largest content will

belong to this class, satisfying (15) with any ǫ ∈ (0, 1/P ), see [11]). Let

:= T

Performing a derivation similar to the one reported in [11], it is possible to show that:

n+1

− τ

≤

∗

(τ

)

1 − ρ

∗

(16)

where the ∗ denotes the quantities corresponding to the buffer selected at time τ

and

∗

. The terms in (16) have been obtained as follows: the ﬁrst term

∗

(τ

)

1−ρ

∗

corresponds to the time to bring the buffer x

∗

from its initial level x

∗

(τ

) to a value

below N

and is derived from [11] setting the setup time δ to 0 and considering that we

only need to reach a value below N

and not 0; the second term

∗

takes into account

that when a buffer is selected, perhaps its content is less than N

. We deﬁne, as in [11]:

w(k) =

i,j

(k)

Then we have:

w(τ

n+1

) =

i,j

(τ

n+1

) =

i,j6=∗

(τ

) + d

(τ

n+1

− τ

)] +

∗

(τ

n+1

)

= w(τ

) +

i,j6=∗

(τ

n+1

− τ

) +

∗

(τ

n+1

) − x

∗

(τ

)]

≤ w(τ

) +

i,j6=∗

(τ

n+1

− τ

) +

∗

−

∗

(τ

)

where the last inequality is implied by the fact that x

∗

(τ

n+1

) ≤ N

(we stop processing

∗

at time τ

n+1

, when its content is below N

). Exploiting (16),

w(τ

n+1

) ≤ w(τ

) +

i,j6=∗



∗

(τ

)

1 − ρ

∗



∗

−

∗

(τ

)

Now, introducing the notation ρ :=

i,j

, we have that

i,j6=∗

= ρ − ρ

∗

Introducing this in the equation above and simplifying, we get:

w(τ

n+1

) ≤ w(τ

) −

∗

(τ

)

1 − ρ

∗

Using (15), the previous becomes:

w(τ

n+1

) ≤ w(τ

) −

∗

i,j

(τ

)

1 − ρ

∗

≤ w(τ

) −

∗

i,j

(τ

)

1 − ρ

∗

where

= max

. So,

w(τ

n+1

) ≤ w(τ

)



1 − ǫ

∗

1 − ρ

∗



∗

Notice that condition (14) under strict inequality can be written as ρ < 1, which is

exactly the condition considered in [11]. The proof can be continued exactly as in [11]

where, however, for us α

1−ρ

(the same as in [11]) and β

. So, as in

[11], it is possible to obtain:

sup

w(τ

) ≤

max

hence

w(t

) ≤

max

+ ρ

where d

= min

. This allows to obtain that

) ≤

w(t

) ≤

max

+ ρ

is bounded for all t

(where

:= min

). 

4 Optimization

Consider for now Q = 1 (one part type system). Now, under condition (14), if every-

thing is approximated through continuous variables, the optimal policy is myopic [12],

that is, it is the cµ rule if dealing with a linear cost function g(x) as the one consid-

ered in (7). The cµ rule consists in processing the buffers B

according to a priority

established by the product c times µ, where in the present problem, the cost coefﬁcient

c associated to the buffer B

is given by the coefﬁcient c

in (7) and the maximum

processing rate µ for this buffer is given by µ

: this is actually the maximum

processing capacity for goods with destination (route) i. There are however two major

differences:

– vehicles are not continuous resources;

– the capacity allocation has an inﬂuence also on the future (if we allocate all vehicles

to destination i we have to wait T

time units before we can change allocation)

while in the scheduling machine case, where the cµ policy has been proved optimal,

capacity allocations can change instantaneously at each step.

4.1 A Possible Heuristic

According to the above observations, we propose here a policy that we believe repre-

sents a promising and simple real time rule. We do not give here a proof of optimality

for this policy and neither give a proof of stability: the performance of this policy will

be explored from a computational point of view. According to the simulations, the sta-

bility appears to hold whenever condition (14) holds: this is not surprising since the

policy reported below reduces the idle periods with respect to the one considered in the

proof of the sufﬁciency of Theorem 1. This depends on the fact that, even if also this

policy (as the one considered in the proof of Theorem 1) does not allow vehicles to

travel partially loaded, it is no more required here that all the vehicles travel together to

the same destination.

In particular, at each time step, the policy considered in this section allocates the ve-

hicles available at that moment to the buffer B

which, among the ones with

≥

1 (that is, among the ones which allow to complete the load of a vehicle) has the largest

cµ index (where, as mentioned above, for the buffer B

, the index cµ is given by

). To illustrate the policy more in detail, assume for simplicity Q = 1 and

let i

, . . . , i

be the priority established according to the cµ rule (that is c

≥

k+1

for all k). Then, the policy is given by:

(k) = min {N

(k), ⌊x

(k)⌋}

(k) = min {N

(k) − n

(k), ⌊x

(k)⌋}

and so on, where N

(k), deﬁned in (3), is the numberof available vehicles in the interval

, t

k+1

). Then, to ﬁll all the vehicles assigned to route i, we set:

(k) = n

(k).

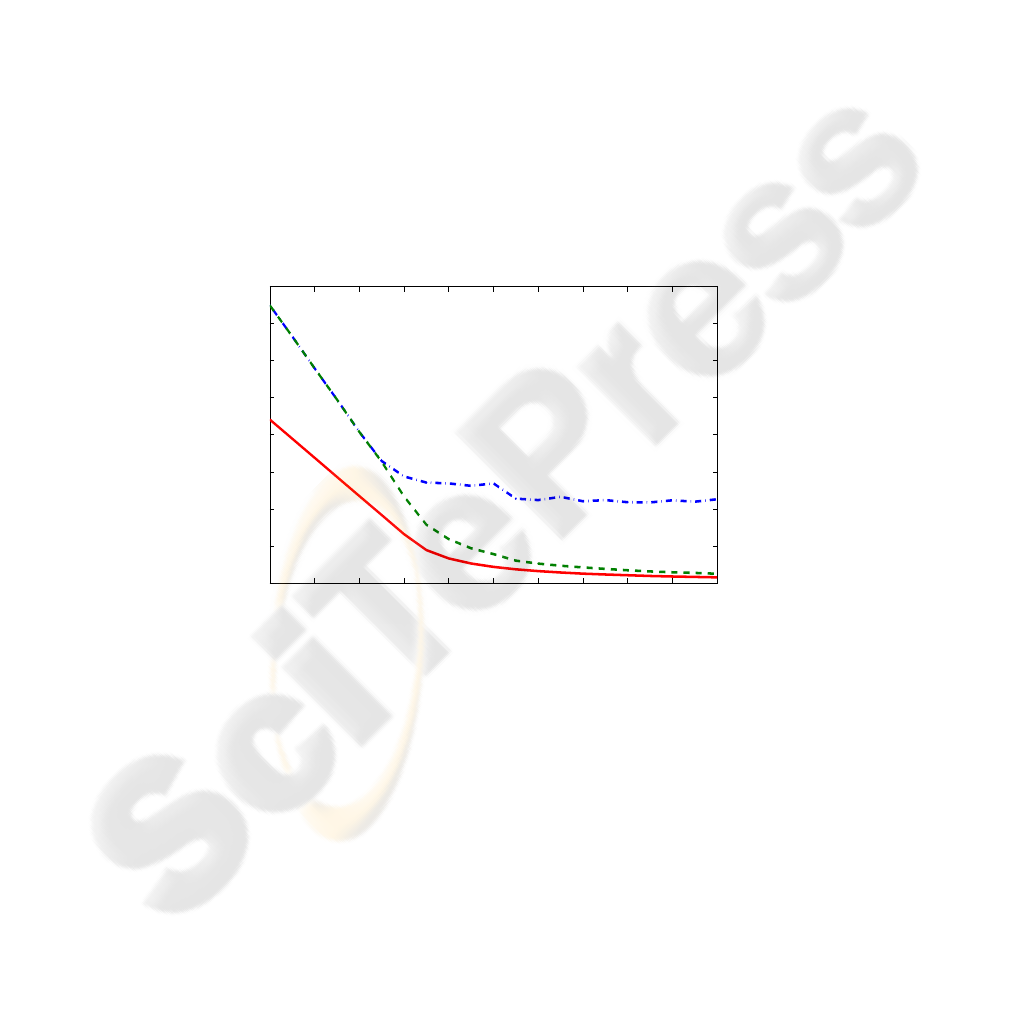
4.2 Simulative Results

We tested the policies discussed above in a system with Q = 1 (a single product), P =

3, characterized by the following parameters: delays T

= 4, T

= 3 , T

= 5 ; arrivals,

constant in time, d

= d

= 7, d

= 5; with this choice the minimum N

guaranteeing

stability is 74,according to condition (14). In ﬁgure are shown the performances(6), (7),

with unit costs c

= c

= 1, c

= 2, and γ = 1, of three policies derived by simulating

the system, for a ﬁnite time horizon, for various values of the parameter N

. The dash

dotted line shows the performances of the stabilizing policy described in Theorem 1;

the dashed line the performances of the policy which allocates at each time instant all

the available vehicles prioritizing the buffers with higher content, and the continuous

line the performances of the “cµ policy” (those coefﬁcients, by the parameters chosen,

make buffer 2 the one with higher priority followed by buffer 1 and 3).

It is possible to observe that for values of N

lower than the stabilizing value (74),

none of the policy described can achieve stability, consistently with Theorem 1 (for

< 74 the costs reported in Figure 1 result ﬁnite as a consequence of the ﬁnite

time horizon considered). For N

> 74 the cµ policy performs better than the policy

prioritizing the higher buffers.

70 72 74 76 78 80 82 84 86 88 90

0.5

1.5

2.5

3.5

x 10

Fig.1. Performances of the cµ policy (continuous line), the serve-largest-buffer policy (dashed),

and the basic stabilizing policy (dash-dotted), as a function of N

5 Conclusions

In this paper, a simpliﬁed model of a logistic node has been considered, where items

arrive from outside to the node and must be routed to different destinations. Waiting

items are stored in different buffers, according to their class and destination. At ﬁrst,

a necessary and sufﬁcient condition is given in the paper for the possibility of ﬁnding

dispatching dynamic policies that maintain all the buffers bounded. Subsequently an

optimization problem is considered and a simulative comparison of the performance of

different feedback policies is presented in the paper. The problem has been studied un-

der a ﬂuid approximationof the items traveling in the node: this allows to completely ﬁll

the vehicles (and to neglect complex combinatorial loading problems). This possibility

is actually used by the policies studied in this paper that do not allow the vehicles to

travel partially ﬁlled. This is actually a reasonable choice under heavy trafﬁc conditions

where allowing the possibility of sending partially full vehicles may even compromise

the stability, but may become signiﬁcantly sub-optimal in the case of reduced inﬂow

rates, large holding costs and small traveling costs.

References

1. T. G. Crainic “Long Haul Freight Transportation” Handbook of Transportation Science, R.W.

Hall (Ed.), 2nd Edition, Kluwer, 2002

2. Carvalho, T.A. and Powell, W.B. “A Multiplier Adjustment Method for Dynamic Resource

Allocation Problems” Transportation Science, 34(2):150-164 (2000).

3. W. Powell, J. Shapiro, and H. Simao. “A Representational Paradigm for Stochastic, Dynamic

Resource Transformation Problems” Annals of Operations Research, 104:231-279, 2001

4. Jinghua Xu; Hancock, K. L.; “Enterprise-wide freight simulation in an integrated logistics

and transportation system”, IEEE Transactions on Intelligent Transportation Systems, Vol-

ume 5, Issue 4, Dec. 2004, 342 - 346

5. Powell, W.B. and Carvalho, T.A. “Dynamic Control of Logistics Queueing Networks for

Large-Scale Fleet Management”, Transportation Science, 32(2):90-109. 1998

6. Powell, W.B. and Carvalho T.A., “Real-Time Optimization of Containers and Flatcars for

Intermodal Operations”, Transportation Science, Vol. 32, No. 2, 110-126, 1998

7. Yang, J., Jaillet, P. and Mahmassani, H. S., “Real-time multi-vehicle truckload pick-up and

delivery problems”, Transportation Science, Vol. 38, 135-148, 2004

8. L.C. Dall’Orto, T.G. Crainic, J.E. Leal and W.B. Powell, “The single-node dynamic service

scheduling and dispatching problem”, European Journal of Operational Research, 170, pp.

123, 2006

9. M. G. Speranza, and W. Ukovich, “Minimizing Transportation and Inventory Costs for Sev-

eral Products on a Single Link”, Operations Research, Vol. 42, No. 5, pp. 879-894, 1994

10. L. Bertazzi, “Analysis of Direct Shipping Policies in an Inventory-Routing Problem with

Discrete Shipping Times”, Management Science, Vol. 54, No. 4, April 2008, pp. 748762

11. J.R. Perkins and P.R. Kumar, “Stable, Distributed, Real-Time Scheduling of Flexible Man-

ufacturing/Assembly/Disassembly Systems,” IEEE Transactions on Automatic Control, Vol.

34, no. 2, February 1989

12. F. Martinelli, C. Shu, and J. Perkins. “On the optimality of myopic production controls for

single server, continuous ﬂow manufacturing systems.” IEEE Transactions on Automatic

Control, 46(8):12691273, 2001

13. P. Chen, Z. Fu, A. Lim, and B. Rodrigues “Port Yard Storage Optimization” IEEE Transac-

tions on Automation Science and Engineering Vol. 1, No. 1, July 2004

14. E. K. Bish, F. Y. Chen, Y. T. Leong, B. L. Nelson, J. W. Cheong Ng, and D. Simchi-Levi

“Dispatching vehicles in a mega container terminal” OR Spectrum, 27, 491-506 (2005)

15. S. Kang, J. C. Medina, and Y. Ouyang, “Optimal operations of transportation ﬂeet for un-

loading activities at container ports” Transportation Research Part B 42 (2008) 970984