ITEM-USER PREFERENCE MAPPING WITH MIXTURE MODELS

Data Visualization for Item Preference

Yu Fujimoto

Dept. Integrated Information Technology, Aoyama Gakuin Univ., Kanagawa, Japan

Hideitsu Hino, Noboru Murata

Dept. Electrical Engineering and Bioscience, Waseda Univ., Tokyo, Japan

Keywords:

Bradley-Terry model, Mixture model, EM algorithm, Preference map, Data visualization.

Abstract:

In this paper, we propose a visualization technique of a statistical relation of users and preference of items

based on a mixture model. In our visualization, items are given as points in a few dimensional preference

space, and user speciﬁc preferences are given as lines in the same space. The relationship between items and

user preferences are intuitively interpreted via projections from points onto lines. As a primitive implementa-

tion, we introduce a mixture of the Bradley-Terry models, and visualize the relation between items and user

preferences with benchmark data sets.

1 INTRODUCTION

In a market research study or an item recommenda-

tion system, it is very important to model and inter-

pret a statistical relation of “users” and “preference of

items” based on a data set. Visualization of such mod-

els helps us to discover new relations between items

and users, e.g. unknown preference tendency for a

speciﬁc user. And visualization also supports to inter-

pret results of item recommendation in systems.

It has an old history to model preference levels

of items from the statistical aspect. Most researchers

assume that a preference parameter θ

is attached to

the item T

for I different items (Bradley and Terry,

1952; Luce, 1959; Plackett, 1975). With this param-

eter, favorable or unfavorable items for users are in-

tuitively interpreted. However, the preference param-

eter potentially has absurdity, because it is obtained

based on data which reﬂect various users’ average,

and the one-dimensional preference assumption may

cause a wrong interpretation. Then, an idea of mul-

tiple preferences, which is an assumption that a user

evaluates an item comprehensively with some indices

such as one’s interest and credibility of the item, is

naturally introduced. For representation of multiple

preferences, some applications of mixture models are

proposed (Croon and Luijkx, 1993; Murphy and Mar-

tin, 2003).

In this paper, we propose a visualization of re-

lation between items and users to assist analysis of

multiple preferences based on mixture models. In our

visualization, items are mapped in a K-dimensional

space associated with K preference coordinates and

their levels on a user speciﬁc preference are shown

as projections onto a line on the map. With this map-

ping, preference relation between items and user pref-

erences can be visually interpreted.

This paper is composed as follows. In Section 2,

a simple probability model with preference parame-

ters, broadly known as the Bradley-Terry (BT) model,

and its mixtures are introduced. In Section 3, an

idea for preference mapping which visualizes the item

preference is explained. We also mention differences

among other visualization tools and our method. Sec-

tion 4 shows experimental results of the item prefer-

ence mapping based on mixtures of BT models. And

Section 5 is devoted to concluding remarks.

2 PREFERENCE MODEL AND

ITS MIXTURE

Let T

be the i-th item where i = 1, . . . , I. Here, a pref-

erence parameter set θ = {θ

, . . . , θ

} is introduced to

represent relative preference levels for I items. Statis-

105

Fujimoto Y., Hino H. and Murata N. (2009).

ITEM-USER PREFERENCE MAPPING WITH MIXTURE MODELS - Data Visualization for Item Preference.

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval, pages 105-111

DOI: 10.5220/0002274001050111

 SciTePress

tical models denoted with such a preference parame-

ter set are called preference models in this paper. We

introduce a simple preference model, the BT model

(Bradley and Terry, 1952), and its mixture.

2.1 Bradley-Terry Model

Assume that a user evaluates two items T

and T

with

ratings r

, r

∈ N, and each user chooses a preferred

item from T

and T

by comparing r

and r

. Let

≻ T

be the event r

> r

, which indicates that T

is chosen in the comparison of T

and T

, and X

be a

variable for the comparison result which takes one of

≻ T

, T

≻ T

}. In the BT model, the probability

that “the item T

is preferred in the comparison of T

and T

”, denoted as p(T

≻ T

;θ), is given by

p(T

≻ T

;θ) =

+ θ

(i 6= j), (1)

where

∑

i=1

= 1, θ

> 0 (i = 1, . . ., I).

Intuitively speaking, the item T

which has larger θ

is chosen more frequently, and θ indicates a set of

preference levels which is common to N users.

Let X

= {X

|1 ≤i < j ≤I}be all the paired com-

parisons in I items, compared by the n-th user. Under

the assumption that each comparison is independent,

the probability Pr(X

= x

) = p(x

;θ), where x

is an

observation from the n-th user, is given by

p(x

;θ) =

∏

i6= j



+ θ



, (2)

where c

is an indicator, that is

, c

) =











(1, 0) (x

= T

≻ T

)

(0, 1) (x

= T

≻ T

)

(0, 0) (x

is missed).

(3)

Note that (c

, c

) = (0, 0) indicates that the compar-

ison x

is missed because the items T

or/and T

are

not rated, or their ratings are the same

With Eq.(2), the log likelihood of x

1:N

, . . . , x

} is given as follows,

L(θ) =

∑

n=1

log p(x

;θ) =

∑

n=1

∑

i6= j

log

+ θ

∑

i6= j

log

+ θ

, (4)

The modeling of paired comparison data with ties (r

) also has a long history (Rao and Kupper, 1967; Davidson

and Beaver, 1977; Joe, 1990; Kuk, 1995), though tied cases

are neglected for simplicity in this paper.

where c

∑

n=1

The maximum likelihood (ML) estimation proce-

dure for the BT model, which achieves

θ = argmax

∑

i6= j

log

+ θ

, (5)

has been already discussed from several contexts, and

some iterative estimation methods for the ML esti-

mator

θ have been introduced (Hastie and Tibshirani,

1998; Huang et al., 2006). In this paper, the estima-

tion is achieved by the following algorithm used in

Huang et al.(2006).

Algorithm 1. Estimation of BT model.

input pairwise comparison data x

1:N

initialize t = 0, and choose an initial parameter θ

(0)

repeat until convergence

update

(t+1)

←

∑

j6=i

∑

j6=i

(t)

+θ

(t)

, (6)

for i = 1, . . . , I.

normalize θ

(t+1)

and set t ← t + 1.

output converged parameter vector θ.

2.2 Mixture Model

In the previous subsection, the BT model was ex-

plained. In this subsection, a mixture of BT models

and its estimation method are introduced.

We assume that “users evaluate items based on K

preference parameter sets with their own weights“,

and introduce a mixture model whose component re-

spectively represents a preference from a different

point of view. Under this assumption, the distribution

of X

is given by the mixture of preference models,

p(X

) =

∑

k=1

p(M

)p(X

), (7)

where M

is the k-th preference model with the pa-

rameter set θ

= {θ

, . . . , θ

} and p(X

) is given

by Eq.(2) with the parameter set θ

. And the log like-

lihood for x

1:N

is given as

L(Θ) =

∑

n=1

log

∑

k=1

p(M

)p(x

), (8)

where Θ = {θ

, . . . , θ

} is the set of parameters for

the mixture.

Since the direct maximization of Eq.(8) is com-

plex, we apply the EM algorithm (McLachlan and Kr-

ishnan, 1996) to estimate the mixture of BTs. The ob-

jective function, so-called the Q-function, for the EM

KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval

106

estimation is deﬁned as follows,

Q(Θ;Θ

(t)

)

∑

n=1

∑

k=1

p(M

;Θ

(t)

)log p(x

;Θ) (9)

∑

n=1

∑

k=1

p(M

;Θ

(t)

)

∑

i6= j

log

+ θ

∑

k=1

∑

i6= j

k(t)

log

+ θ

, (10)

where w

k(t)

∑

n=1

p(M

;θ

k(t)

). We call

p(M

) user weight. With this function, a procedure

for the EM estimation is denoted as follows.

Algorithm 2. The EM estimation.

input pairwise comparison data x

1:N

initialize t = 0, and choose an initial parameter Θ

(0)

repeat until convergence

E-step: calculate user weight p(M

;Θ

(t)

) of Eq.(9)

p(M

;Θ

(t)

) =

∏

i6= j

k(t)

+θ

k(t)

∑

m=1

∏

i6= j

m(t)

+θ

m(t)

. (11)

M-step: maximize the Q-function given by Eq.(10)

with respect to Θ, that is equivalent to

k(t+1)

= argmax

∑

i6= j

k(t)

log

+ θ

(12)

for all k, and set t ←t + 1.

output converged parameter vector

Θ.

Note that Eq.(12) is equivalent to Eq.(5) and the

maximization is achieved based on Algorithm 1 by

using w

k(t)

instead of c

. As broadly known, the EM

algorithm is the local maxima algorithm. In our ex-

periments, therefore, models are estimated ﬁve times

from randomly chosen initial parameters, and the one

which achieves the highest Q-value is used.

For selection of the optimal K, the information cri-

teria (Akaike, 1974; Barron et al., 1998) or cross val-

idation (CV)(Hastie et al., 2001) are applicable. In

Section 4, we use CV to select K.

3 PREFERENCE MAPPING

As deﬁned in Section 2, preference models have pa-

rameters to represent preferences for I items. With

0.0 0.1 0.2 0.3 0.4 0.5

√

Figure 1: An example of preference mapping in one-

dimensional case. Items are plotted according to the square

root of θ to facilitate visualization.

0.0 0.2 0.4 0.6 0.8 1.0

T 1

T 2

T 3

T 4

T 5

√

Figure 2: An example of 2D preference mapping.

a mixture of K preference models, an item T

can

be mapped on a K-dimensional space and its coor-

dinate (θ

, . . . , θ

) gives us an intuitive interpretation

of preference relation. In this section, we propose an

intuitive preference mapping tool based on a mixture

model.

3.1 Item Mapping

By introducing a preference model, the preference

tendency of each item is interpreted intuitively by

plotting the parameter on an axis. Figure 1 shows an

example of such a plot. It is visually understood that

tends to be preferred as shown in the ﬁgure. We

call this type of plot a preference map

In the case of a mixture model, θ

shows one of

the K coordinates for representation of preference lev-

els. Accordingly, the multiple preference parameters

with K ≥ 2 can be mapped in a K-dimensional space

in the same way. Figure 2 shows an example of two-

dimensional preference mapping of I = 15 items. On

a 2D preference map, those items which are com-

monly preferred by various users, like T

, are mapped

on the upper right side in the ﬁgure, and not preferred

items in one dimension are mapped near the other

axis, like T

and T

In this paper, all the axes in preference maps are given

in the square root of preference parameters for easy-to-see

visualization though it is not essential.

ITEM-USER PREFERENCE MAPPING WITH MIXTURE MODELS - Data Visualization for Item Preference

107

0.0 0.2 0.4 0.6 0.8 1.0

T 1

T 2

T 3

T 4

T 5

√

Figure 3: Preference mapping in a 2D space. A solid line

in the map shows a user preference weight and dotted lines

show projections onto the user preference levels which in-

dicates φ

0.0 0.1 0.2 0.3 0.4 0.5

√

Figure 4: An example of a user preference φ

. Plots are

corresponding to the projected items onto the line in Figure

3.2 User Preference

As previously denoted, we assume that “users evalu-

ate items based on K preference parameter sets with

their own weights” for the mixture model, and a

user preference weight can be shown as a vector

(p(M

), . .. , p(M

)) in a preference map. The

direction of this vector expresses that the user thinks

which coordinate is more important. For example, the

solid line in Figure 3 shows a user preference weight

for the user n which has tangents of

p(M

)

p(M

)

. The line

indicates that the user rely on both of the axes θ

and

Additionally, we can obtain a user speciﬁc prefer-

ence levels {φ

} of {T

} by projecting items onto the

line on the map. Figure 3 also shows an example of

item projections given as dotted lines to represent user

preference levels. Projected points on the line indicate

us the one-dimensional preference levels for the n-th

user (see, Figure 4) embedded in the K-dimensional

space. Such a projection can be expressed with the

coordinate of T

and the user preference weight. For

example, one can easily come up with a projection

given by the simple mixture of K parameters: a level

of T

on the n-th user preference is given by

∑

k=1

p(M

)θ

. (13)

Projection deﬁned by Eq.(13) is called linear projec-

tion in this paper. For another example, a projection

given by the mixture of K parameters in a sense of the

single BT estimation is also possible, that is given by

= argmax

∑

j6=l

∑

k=1

p(M

)

+ θ

log

+ φ

(14)

where φ

= {φ

, . . . , φ

}. We call projection deﬁned

by Eq.(14) BT projection. The former type of pro-

jection is very simple however the latter one seems

natural. In Figures 3 and 4, BT projection is applied

to a speciﬁc user preference. In Section 4, two types

of projections are compared.

As denoted at the end of previous section, the op-

timal K for the mixture model can be selected by the

model selection procedure. However we still have a

problem for visualizing preference mapping of a spe-

ciﬁc user. A visualization of mapped items is quite

simple in the low dimensional case, however, in the

case of K ≥ 4, we have to visualize the high dimen-

sional preference map in the low dimensional space.

Here, user weight p(M

) shows that how much the

n-th user emphasizes the k-th preference parameter set

. An informative low dimensional preference map

for the user is obtained by picking up some dimen-

sions with the heaviest user weights. Note that the

preferencemap without visualizing dimensions which

have heavy user weights sometimes provides us mis-

leading information. For example, Figure 5 shows an

informative 2D preference map for a user by picking

up θ

and θ

which havethe two heaviest user weights

in the mixture with K = 4, Figure 6 shows a mislead-

ing 2D preference map for the same user, mapped in

a randomly selected two-dimensional space and Fig-

ure 7 shows the user preference levels φ

. In Figure 5,

the mapped items according to preference map coor-

dinates θ

and θ

roughly reﬂect the user preference

(φ

), e.g. items mapped on the upper right side, like

, are also highly preferred in Figure 7. By contrast,

items mapped on the upper right side in a misleading

preference map do not preserve this relation, e.g. T

in Figure 6 is less preferred than T

in φ

. Such a con-

ﬂict happens because the low dimensional space with

small p(M

) does not have valid information about

the n-th user.

3.3 Other Mapping Tools

As a tool for visualization of probabilistic re-

lation between evaluated items and users, the

Multi-Dimensional Scaling (MDS) or the Multi-

Dimensional unfolding (Bennett and Hays, 1960) has

been proposed. Especially the Multi-Dimensional un-

folding is a method to map items and users in a low

KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval

108

0.0 0.2 0.4 0.6 0.8 1.0

T 1

T 2

T 3

T 4

T 5

√

Figure 5: An example of informative 2D preference map-

ping of the mixture with K = 4.

0.0 0.2 0.4 0.6 0.8 1.0

T 1

T 2

T 3

T 4

T 5

√

Figure 6: An example of misleading preference mapping.

0.0 0.1 0.2 0.3 0.4 0.5

√

Figure 7: User preference levels φ

corresponding to the

lines in Figure 5 and Figure 6.

dimensional space according to user preference lev-

els of items. Even in recent years, some researchers

also have proposed the preference visualization (Mei

and Shelton, 2006; Zenebe and Norcio, 2007). An ob-

vious difference between their works and ours is the

representation of user preference in the map. In our

method, items are mapped in the K-dimensional space

and their preference levels for each user are given by

projections onto the corresponding line whose direc-

tion indicates the user weight: i.e. how much this user

relies on the axes of the graph relatively. We avoid to

map users and items as points on the same space be-

cause they are not the same kind of data.

To visualize relations between items and user pref-

erences with points and lines, the Arrow and Point

Method (APM) (Hayashi, 1993) has been also pro-

posed. The APM achieves similar mapping as our

method, and also shows the relation between items

and users by points and lines. However the map ob-

tained by our method shows K universal preference

coordinates at the same time and intuitively inter-

preted from a statistical viewpoint, which is a discrim-

inative point that the APM does not have.

4 EXPERIMENTS

In this section, we discuss our visualization method

on real-world data sets. At ﬁrst, we show the exper-

imental results of tuning the optimal K in a way of

the conventional statistical model selection. Then, we

evaluate a structure of the preference mapping which

is deﬁned by a mixture of preference models from

a viewpoint of precision of user preferences with a

ranking correlation metric.

4.1 Real-world Data Sets

The MovieLens data set is a standard benchmark data

set provided by GroupLens research team (Riedl and

Konstan, 2000). This data set contains 100, 000 rat-

ings answered by N = 943 users for I = 1, 682 movies.

The BookCrossing data set is another benchmark

data set which contains ratings of books (Ziegler

et al., 2005). To obtain dense paired comparison set

for evaluating our preference mapping, we removed

answers rated as 0 and picked up 4, 282 ratings an-

swered by N = 799 users for I = 200 items.

We use these two data sets for evaluation of our

mixture model and preference mapping.

4.2 Evaluation Metric

For a metric of the mapping precision, we use the

ranking correlation between rating data and user pref-

erence levels. Let r

and r

be ratings of T

and T

evaluated by the n-th user. For items evaluated by the

user, if the ordering of r

and r

is the same as the

ordering of φ

and φ

, a pair (T

, T

) is called con-

cordant. On the other hand, if the two orderings are

different, the pair is called discordant. In the case of

ties, that is r

= r

(or/and φ

= φ

), the pair is neither

concordant or discordant. Then the metric is given as

follows

−N

+ N

, (15)

where N

) is the number of concordant (discor-

dant) pairs, and N

) is the number of ties in rat-

ings (preference levels) of the n-th user. Equation (15)

is called Kendall’s tau-b, and used for evaluating the

correlation between two ranking sequences with ties

(Mei and Shelton, 2006). Note that the tau-b metric

ITEM-USER PREFERENCE MAPPING WITH MIXTURE MODELS - Data Visualization for Item Preference

109

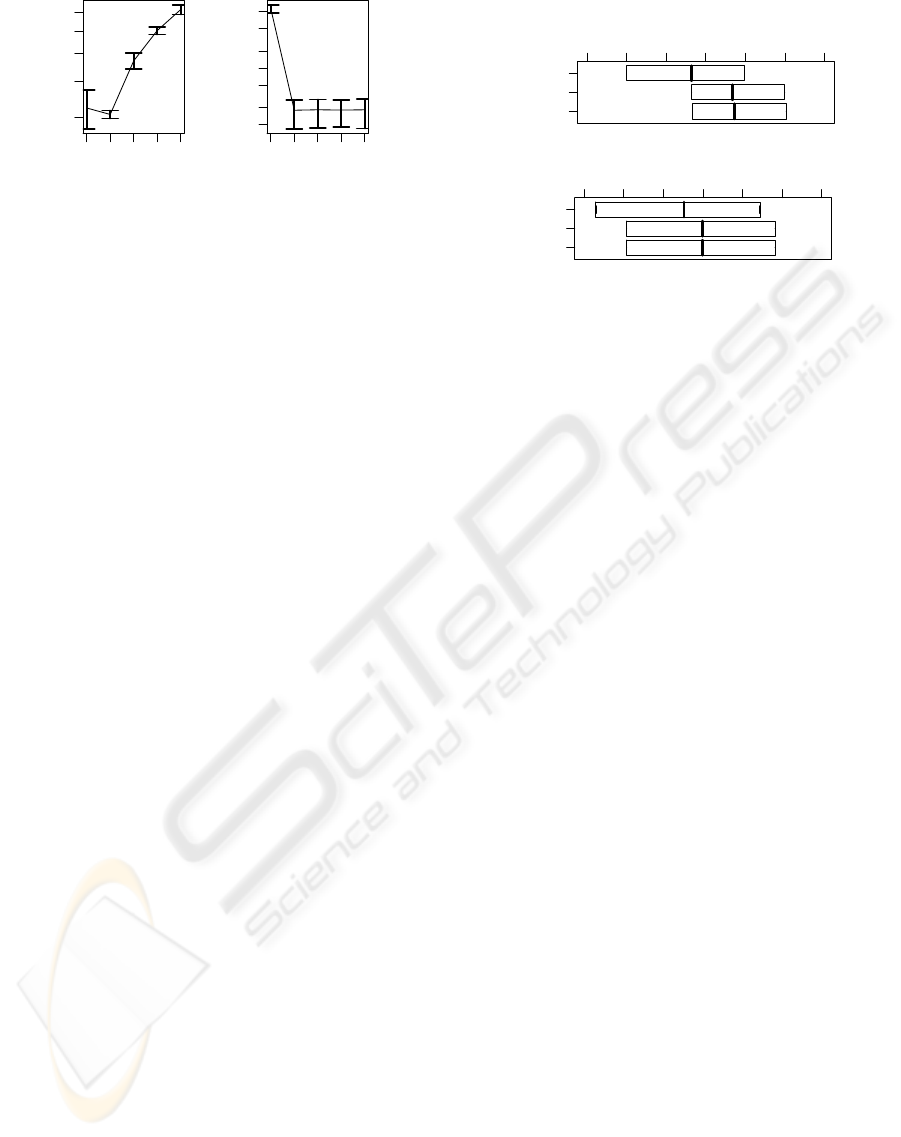
1 2 3 4 5

300 400 600

negative log likelihood

1 2 3 4 5

1e+04 1e+05 1e+06

negative log likelihood

Figure 8: Plots of 5-fold CV results of the negative log

likelihood: left one is the result of BookCrossing data and

right one is that of MovieLens data. The vertical bars in the

graphs show standard deviations.

is −1 ≤ τ

≤ 1, and τ

∼

1 (τ

∼

−1) indicates the

orderings of the ratings and the user preferences are

strongly positive (negative) correlated. And τ

= 0

indicates their orderings are independent. Note that

the tau-b metric is calculated between all the pairs of

ratings and user preference levels such that c

= 1 for

each user. In the next subsection, we experimentally

show that the mixture of preference models achieves

precise mapping in the viewpoint of the tau-b metric.

4.3 Experimental Results

To visualize preference maps of the BookCrossing

data and the MovieLens data, the optimal K is se-

lected based on 5-fold CV. The results (Figure 8)

showthat K = 2 is selected for both of the BookCross-

ing data and the MovieLens data in the sense of the

one standard deviation rule. Figure 9 shows simpli-

ﬁed distributions of tau-b values between ratings and

user preferences, deﬁned by Eq.(15), of N users. A

user preference φ

is calculated under the optimal K

selected by CV (i.e. K = 2) and two types of projec-

tions (linear and BT projections) are applied to derive

. And the tau-b values between ratings and θ in the

single BT model is also plotted in Figure 9 for com-

parison. In the ﬁgure, mixtures with the both projec-

tions apparently improve tau-b values and the results

show that the mixture organizes more precise prefer-

ence than the single preference model for each user.

In other words, ranking of ratings corresponds to that

of φ

on each user preference more speciﬁcally by in-

troducing mixture of preference models. The ﬁgure

also shows that precision of ranking estimation with

user preference based on the simple linear projection

is approximately the same as that of the BT projec-

tion.

Figure 10 shows 2D preference maps as a result of

the experiment on the BookCrossing data set. The left

ﬁgure is the map with a user preference of those who

rely on θ

. For such a user, items which have a higher

Single BT

Linear proj.

BT proj.

−0.2 0.0 0.2 0.4 0.6 0.8 1.0

tau−b

Single BT

Linear proj.

BT proj.

0.20 0.25 0.30 0.35 0.40 0.45 0.50

tau−b

Figure 9: Plots of tau-b values. The line in each box indi-

cates the median of tau-b for N users, and the vertical edges

of the box indicate the 75% and 25% quantiles.

value in θ

, like T

171

shown as a ﬁlled square in the

ﬁgure, are attractive (see the upper right ﬁgure). On

the other hand, the middle ﬁgure is the map with the

index of those who rely on θ

. For such a user, an item

like T

shown as a ﬁlled circle is preferred (see the

lower right). As the result, we can say that preference

maps like Figure 10 has a potential of visualization

which indicates not only relations between items but

also differences between each user preference.

5 CONCLUSIONS AND FUTURE

WORKS

This paper proposes a method to visualize multiple

preferences of items, with a mixture of preference

models. We adopt BT models for simple implementa-

tion of preference model in this paper, while the mix-

ture can be composed of not only BT models but also

any probability models for preference levels. Actu-

ally, as described in Hastie and Tibshirani (1998), the

conventional BT model sometimes leads to the inac-

curate preference parameter θ which does not reﬂect

the preference order of items. To avoid this prob-

lem, a mixture of modiﬁed BT models, such as Huang

et al. (2006), or alternative preference models (Luce,

1959; Plackett, 1975; Hino et al., 2009) should be

applied. We also conﬁrmed that a preference map

can be drawn with other preference models though it

doesn’t explain in this paper. Regardless of whether

BT models are used, the obtained map based on pro-

posed method is directly interpreted as the probability

model, and provides effective suggestions as the anal-

ysis result, e.g. we can show grounds of the recom-

mendation visually for users.

In our method, items are mapped in the K-

dimensional space, user’s preference weights are

KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval

110

0.0 0.1 0.2 0.3 0.4

T55

T171

√

0.0 0.1 0.2 0.3 0.4

T55

T171

√

0.00 0.05 0.10 0.15 0.20 0.25

T55

T171

√

0.00 0.05 0.10 0.15 0.20 0.25

T55

T171

√

Figure 10: Preference maps based on the BookCrossing data set. The left ﬁgure shows a user preference of those who rely on

, the middle one shows that of those who rely on θ

and the right ﬁgures show user preference levels φ

of these users.

given as lines, and user’s own preference levels are

given by projections onto the corresponding line. We

experimentally compared two types of projections,

linear and BT, and veriﬁed that there was no big dif-

ference in results of tau-b metric. As a criterion to vi-

sualize the K-dimensional preference map and a user

preference in a low dimensional space, we focus on

the user weight p(M

). However, when we com-

pare two users, the low dimensional map which accu-

rately shows difference between their preferences is

expected, though it remains as a future work.

REFERENCES

Akaike, H. (1974). A new look at the statistical model iden-

tiﬁcation. IEEE Trans. Automatic Control, 19(6):716–

723.

Barron, A., Rissanen, J., and Yu, B. (1998). The minimum

description length principle in coding and modeling.

IEEE Trans. Information Theory, 44(6):2743–2760.

Bennett, J. F. and Hays, W. L. (1960). Multidimensional

unfolding: Determining the dimensionality of ranked

preference data. Psychometrika, 25(1):27–43.

Bradley, R. A. and Terry, M. E. (1952). Rank analysis of in-

complete block designs: I. the method of paired com-

parisons. Biometrika, 39(3/4):324–345.

Croon, M. and Luijkx, R. (1993). Probability Models

and Statistical Analyses for Ranking Data, chapter 4,

pages 53–74. Lecture Notes in Statistics. Springer.

Davidson, R. R. and Beaver, R. J. (1977). On extending the

Bradley-Terry model to incorporate within-pair order

effects. Biometrics, 33(4):693–702.

Hastie, T. and Tibshirani, R. (1998). Classiﬁcation by pair-

wise coupling. Annals of Statistics, 26(2):451–471.

Hastie, T., Tibshirani, R., and Friedman, J. (2009). The Ele-

ments of Statistical Learning: Data Mining, Inference

and Prediction. 2nd Ed. Springer Series in Statistics.

Springer.

Hayashi, C. (1993). Quantitative social research -belief sys-

tems, the way of thinking and sentiments of ﬁve na-

tions -. Behaviormetrika, 19(2):127–170.

Hino, H., Fujimoto, Y., and Murata, N. (2009). Item prefer-

ence parameters from grouped ranking observations.

In Proc. 13th Paciﬁc-Asia Conference on KDD.

Huang, T.-K., Weng, R. C., and Lin, C.-J. (2006). General-

ized Bradley-Terry models and multi-class probabil-

ity estimates. Journal of Machine Learning Research,

7:85–115.

Joe, H. (1990). Extended use of paired comparison models,

with application to chess rankings. Applied Statistics,

39(1):85–93.

Kuk, A. Y. C. (1995). Modeling paired comparison data

with large numbers of draws and large variability of

draw percentages among players. The Statistician,

44(4):523–528.

Luce, R. D. (1959). Individual Choice Behavior. John Wi-

ley & Sons, Inc.

McLachlan, G. J. and Krishnan, T. (1996). The EM Algo-

rithm and Extensions. Wiley-Interscience.

Mei, G. and Shelton, C. R. (2006). Visualization of collab-

orative data. In Proc. 22nd International Conference

on UAI, pages 341–348. AUAI Press.

Murphy, T. B. and Martin, D. (2003). Mixtures of distance-

based models for ranking data. Computational Statis-

tics & Data Analysis, 41:645–655.

Plackett, R. L. (1975). The analysis of permutations. Ap-

plied Statistics, 24(2):193–202.

Rao, P. V. and Kupper, L. L. (1967). Ties in paired-

comparison experiments: A generalization of the

Bradley-Terry model. Journal of the American Sta-

tistical Association, 62(317):195–204.

Riedl, J. and Konstan, J. (2000). Movielens data set.

http://www.grouplens.org/.

Zenebe, A. and Norcio, A. F. (2007). Visualization of item

features, customer preference and associated uncer-

tainty using fuzzy sets. In Proc. Annual Meeting of

the North American Fuzzy Information Processing So-

ciety, pages 22–32.

Ziegler, C.-N., McNee, S. M., and Konstan, J. A. (2005).

Improving recommendation lists through topic diver-

siﬁcation. In Proc. 14th International World Wide Web

Conference (WWW ’05), pages 22–32.

ITEM-USER PREFERENCE MAPPING WITH MIXTURE MODELS - Data Visualization for Item Preference

111