
DOOR
Towards a Formalization of Ontology Relations
∗
Carlo Allocca, Mathieu d’Aquin and Enrico Motta
Knowledge Media Institute, The Open University, Walton Hall, Milton Keynes, MK7 6AA, U.K.
Keywords:
Ontology Relations, Networked Ontology.
Abstract:
In this paper, we describe our ongoing effort in describing and formalizing semantic relations that link ontolo-
gies with each other on the Semantic Web in order to create an ontology, DOOR, to represent, manipulate and
reason upon these relations. DOOR is a Descriptive Ontology of Ontology Relations which intends to define
relations such as inclusion, versioning, similarity and agreement using ontological primitives as well as rules.
Here, we provide a detailed description of the methodology used to design the DOOR ontology, as well as
an overview of its content. We also describe how DOOR is used in a complete framework (called KANNEL)
for detecting and managing semantic relations between ontologies in large ontology repositories. Applied in
the context of a large collection of automatically crawled ontologies, DOOR and KANNEL provide a starting
point for analyzing the underlying structure of the network of ontologies that is the Semantic Web.
1 INTRODUCTION
Ontologies are the pillars of the Semantic Web (SW)
and, as more and more ontologies are made avail-
able online, the SW is quickly taking shape. As a
result, the research community is becoming more and
more aware that ontologies are not isolated artifacts:
they are, explicitly or implicitly, related with each
other (Kleshchev and Artemjeva, 2005). Indeed, a
number of studies have intended to tackle some of
the challenges raised by these ontology relationships,
from both theoretical and practical points of view.
At a theoretical level, studies have targeted ontol-
ogy comparison in order to identify overlaps between
ontologies (Maedche and Staab, 2002). Approaches
have been proposed to find differences between ver-
sions of an ontologies (Noy and Musen, 2002; Konev
et al., 2008).
According to (Klein and Fensel, 2001), the
ontology versioning problem has been defined as the
ability to handle changes in ontologies by creating
and managing different variants of it. In other words,
ontology versioning means that there are multiple
variants of an ontology around. The authors of (Klein
and Fensel, 2001) suggested that, ideally, developers
should maintain not only the different versions of
∗
This work was funded by the EC IST-FF6-027595
NeOn Project.
an ontology, but also some information about the
way versions differ and whether or not they are
compatible with each other. In (Gangemi et al., 1999)
ontology integration is defined as the construction of
an ontology C that formally specifies the union of the
vocabularies of two other ontologies A and B. The
most interesting case is when A and B commit to the
conceptualization of the same domain of interest or
of two overlapping domains. In particular, A and B
may be related by being alternative ontologies, truly
overlapping ontologies, equivalent ontologies with
vocabulary mismatches, overlapping ontologies with
disjoint domain, homonymically overlapping ontolo-
gies. Finally, in ontology matching, an alignment is
a set of correspondences between the entities of two
ontologies, therefore relating these two ontologies by
mapping there models with each other.
At a practical level, Semantic Web Applications use
the SW as a large-scale knowledge source (d’Aquin
et al., 2008): they achieve their tasks by automatically
retrieving and exploiting knowledge from the SW
as a whole, using advanced Semantic Web Search
Engines (SWSEs) such as WATSON (d’Aquin
et al., 2007). These SWSEs provide keyword based
search mechanisms to locate relevant ontologies
for particular applications. As an example, the
query “student” currently gives 1079 ontologies as
13
Allocca C., d’Aquin M. and Motta E. (2009).
DOOR - Towards a Formalization of Ontology Relations.
In Proceedings of the International Conference on Knowledge Engineering and Ontology Development, pages 13-20
DOI: 10.5220/0002276400130020
Copyright
c
SciTePress

a result in WATSON
2
(valid on the 22/04/2009).
However, these results are provided as a simple
list without making explicit the underlying rela-
tions that link ontologies with each other. Indeed,
on the first page, at least 2 of the ontologies
(http://www.vistology.com/ont/tests/student1.owl
and http://www.vistology.com/ont/tests/student2.owl)
represent, apart from their URIs and the base
namespaces, exactly the same logical model,
expressed in the same ontology language. An-
other common situation is when an ontology
has been translated in different ontology lan-
guages. This is the case in the first and second
results of the query “student, university, re-
searcher”(http://reliant.teknowledge.com/DAML/Mid-
level-ontology.owl and http://reliant.
teknowledge.com/DAML/Mid-level-ontology.daml).
These two ontologies are obviously two different
encodings of the same model. Inspecting the results
of WATSON in the same way, it is not hard to find
ontologies connected with other, more sophisticated
semantic relations: versioning, inclusion, similarity,
etc. Leaving implicit these relations in SWSE’s
ontology repositories generates additional difficulties
in exploiting their results, expecting the users and the
applications to find the “right” or “best” ontology to
achieve their goal.
Both the theoretical and practical challenges con-
cerning relations between ontologies indicate a need
for a general study of these relations, providing a for-
mal base for defining, manipulating and reasoning
upon the links that relate ontologies online, explic-
itly or implicitly. Here, we chose to take an ontolog-
ical approach to this problem. We design DOOR, a
Descriptive Ontology of Ontology Relations that de-
fines ontology relations using ontological primitives
and rules. Apart from the ontology itself, the main
contributions of this work concern the realization of a
methodology to identify and define relations between
ontologies, as well as the development of a complete
system based on DOOR (KANNEL), providing ser-
vices for detecting relations, populating DOOR, and
formally querying detected and inferred relations in a
large ontology repository.
This paper is structured as follows: in Section 2
we continue discussing significant work concerning
ontology relations; Section 3 presents the adopted
methodology for designing DOOR; Section 4 de-
scribes the DOOR ontology; In Section 5 we briefly
describe KANNEL and the main role of DOOR in this
framework. Finally, Section 6 concludes the paper
and sheds the light on interesting future research on
ontology relations.
2
http://watson.kmi.open.ac.uk
2 RELATED WORK
J. Heflin (Heflin and Pan., 2004) was the first to stud-
ied formally some of the different types of links be-
tween ontologies, focusing on the crucial problems of
versioning and evolution. However, currently, there is
no ontology management system that implements his
framework. The authors of (Kleshchev and Artem-
jeva, 2005) characterized, at a very abstract level,
a number of relations between ontologies such as
sameConceptualization, Resemblance, Simplification
and Composition, without providing formal defini-
tions for them, and without considering the links be-
tween these relationships. Several approaches have
been focusing on how to compare two different ver-
sions of ontologies in order to find the differences.
In particular, PROMTDIF (Noy and Musen, 2002)
compares the structure of ontologies and OWLD-
iff (http://semanticweb.org/wiki/OWLDiff) computes
the differences by entailment, checking the two set
of axioms. SemVersion (Volkel, 2006) compares two
ontologies and computes the differences at both the
structural and the semantic levels. In addition, many
measures exist to compute particular forms of simi-
larity between ontologies (David and Euzenat, 2008).
All these studies discuss particular relations sepa-
rately and are generally based on an abstract, informal
definition of the relations they consider. A complete
model is necessary to provide a wide overview of ex-
isting ontology relations, to clearly establish what are
their definitions, formal properties, and how they are
connected with each other.
3 METHODOLOGY FOR THE
DOOR ONTOLOGY
Building an ontology of relationships between ontolo-
gies is a very ambitious task. It requires a deep analy-
sis of the ontologies available online and of the liter-
ature, at different levels. Therefore, a reasonably rig-
orous but nonetheless flexible methodology is needed
to identify, describe and formalize ontology relations
and their connections, in order to build the DOOR on-
tology. Here, after defining some important elements
that will be used in the rest of the paper, we present
the steps involved in the methodology we adopted and
briefly detail each of them.
3.1 Definitions and Requirements
We consider the following definitions:
Definition 1 (Ontology). An ontology is a set of ax-
ioms (in the sense of the description logic) over a Vo-
KEOD 2009 - International Conference on Knowledge Engineering and Ontology Development
14

cabulary VOC, where VOC is the set of the primitive
terms (named entities) employed in the axioms of the
ontology;
Definition 2 (Ontology Space). An ontology space
OS, is a collection of ontologies.
Definition 3 (Ontology Relation). Given an ontology
space OS, an Ontology Relation is any binary relation
defined over OS.
At the most general level, the design of the DOOR
ontology was based on three main sources to identify
relevant ontology relations:
1. We analyzed the results of SWSEs (e.g., WAT-
SON) to manually identify existing, implicit re-
lations between ontologies in these results.
2. We considered relations described in the litera-
ture, such as the ones already mentioned in the
previous sections.
3. We also included existing, explicit relations that
are primitives of the OWL ontology language.
Also, ontology relations in the DOOR ontology
should reflect the following important features:
• they are general enough to be applied to multiple
domains;
• they are sufficiently intuitive to reflect general
meaning;
• they are formally defined to be processed auto-
matically by inference engines;
3.2 Main Steps of the Methodology
To design DOOR, we considered the methodology de-
scribed in (Gangemi et al., 2001) for selecting general
ontological categories and adapted it to the problem
of ontology relations. As a result, we divided our ap-
proach into a number of steps, as follows:
1. Identifying the top level relations between ontolo-
gies, considering our three sources (SWSEs, liter-
ature and existing OWL primitives). At this stage,
the task only consists in coming up with a list of
relations that should be relevant, giving us a gen-
eral overview of the different sections of the on-
tology. Relations such as inclusion, similarity,
incompatibility and previous version are identi-
fied here.
2. Specifying the identified relations, identifying rel-
evant variants and sub-relations. Here, our three
sources of relations are also employed to derive
relations at a lower level. We also use a more sys-
tematic approach, which consists in looking at on-
tologies (and so ontology relations) from 5 differ-
ent dimensions that can characterize them:
• The Lexicographic level, which concerns the
comparison of the vocabularies of the ontolo-
gies.
• The Syntactic level, which concerns the com-
parison of the sets of axioms that form the on-
tologies.
• The Structural level, which concerns the com-
parison of the graph structure formed by the ax-
ioms of the ontologies.
• The Semantic level, which concerns the com-
parison of the formal models of the ontolo-
gies, looking in particular at their logical con-
sequences.
• The Temporal level, which concerns the anal-
ysis of the evolution of ontologies in time.
For example, considering the relation of inclusion
identified in the first step and that led to a
property includedIn in the ontology, we can
specify this relation according to three dif-
ferent dimensions (syntactic, structural and
semantic), leading to three variants of inclusion
between ontologies (syntacticallyIncludedIn,
isHomomorphicTo and semanticallyIncludedIn)
that consider the set of axioms, the graph and
the formal models of the ontologies respectivly.
In addition, besides the systematic analysis of
this relation according to the dimensions, we
include in DOOR particular forms of inclusions
derived from existing OWL primitives (e.g.,
OWL imports) and from the literature (e.g,
isAConservativeExtensionO f (Ghilardi et al.,
2006)). More details about these relations are
given in the next section.
3. Characterizing each relation by its algebraic prop-
erties. For example, the algebraic properties for
similarity are that it is re f lexive and symmetric.
For inclusion, we can define that it is re f lexive
and transitive. Including such information in the
ontology corresponds to what (Gangemi et al.,
2001) calls defining the ground axioms.
4. Establishing connections between relations. The
results obtained from the previous steps are
mainly top-level relations with a list of variants,
each of them being given algebraic properties.
Here, we want to structure these lists, in partic-
ular by giving them taxonomic relations. As an
example, it can be easily established that syn-
tacticallySimilarTo is a sub property of semanti-
callySimilarTo. In the same way, we can indicate
that a previous version of an ontology ought to be
similar to it. This corresponds to defining non-
ground axioms in (Gangemi et al., 2001).
DOOR - Towards a Formalization of Ontology Relations
15

ontologyRelatedTo
agreesWith disagreesWith includedIn isAlignedTo isTheSchemaFor
similarTo
Figure 1: Top Level of DOOR.
5. Introducing rules to define complex relations from
atomic ones. For example, the equivalentTo
property can be defined as equivalentTo(X
1
, X
2
):-
includedIn(X
1
, X
2
), includedIn(X
2
, X
1
).
Like in any methodology, the application of these
steps should be flexible and continuous. Getting back
to a previous step is sometimes necessary and, as the
building of an ontology such as DOOR is a constantly
ongoing effort, it should be possible to re-apply the
methodology entirely to make the ontology evolve.
The intended result is an ontology made, on the
one hand, of an ontologically defined and taxonomi-
cally structured set of relations, and on the other hand,
of a set of rules to define complex relations. In the
following we give a detailed overview of the first ver-
sion of the DOOR ontology, considering only the first
(ontological) part of it, as, due to its complexity, the
definition of rules governing complex relations is still
a work in progress and would not fit in this paper.
4 FORMAL DESCRIPTION
OF DOOR
The OWL version of the DOOR
ontology can be downloaded at:
http://kannel.kmi.open.ac.uk/ontology. We start
with describing the first level of DOOR, in Figure
2. The main relevant abstract relations are simply
represented as sub-properties of ontologyRelatedTo.
An ontology X is ontologyRelatedTo another one Y
if one of the top level relations is satisfied between
X and Y. The top level relations include includedIn,
similarTo, isAlignedTo, disagreesWith, agreesWith
and isTheSchemaFor. We clustered them in four
groups and each group will be explained in more
details in the next sub-sections.
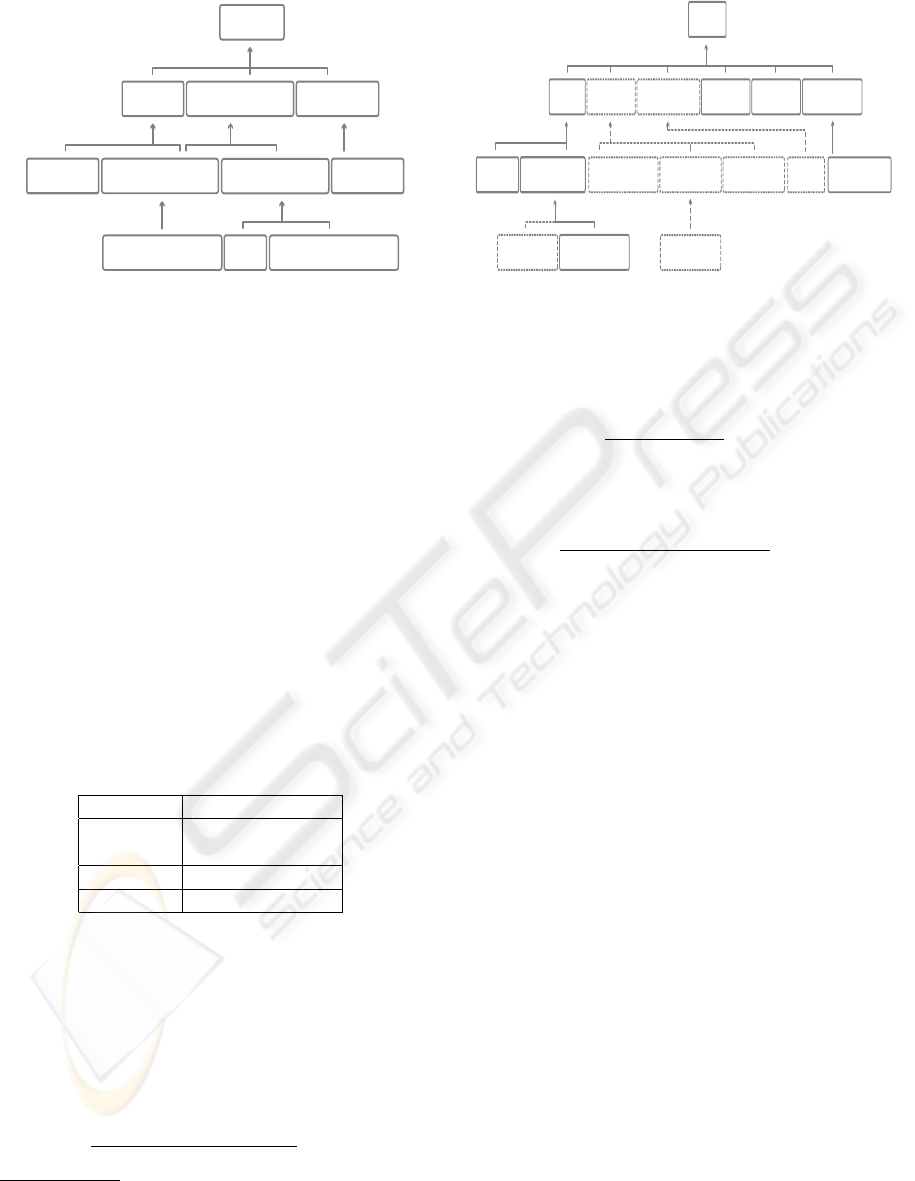
4.1 includedIn and equivalentTo
includedIn and equivalentTo are two of the main on-
tology relations. The former represents the meaning
of “an ontology contains an another one”. The lat-
ter intends to convey the meaning of “two ontolo-
gies express the same knowledge”. According to our
methodology, these two relations have been analyzed
at different levels, giving origin to different kinds of
inclusion and equivalence relations. In Table 1, we
summarize the result of these analyses:
Table 1: Specialization of inclusion and equivalence rela-
tions.
includedIn equivalentTo
Semantic semanticallyIncludedIn semanticallyEquivalentTo
isAConservativeExtentionOf
Structural isHomomorphicTo isIsomorphicTo
Syntactic syntacticallyIncludedIn syntacticallyEquivalentTo
import
In particular, the sub-relations of includedIn are de-
fined as follows:
syntacticallyIncludedIn(X
1
, X
2
) if the set of axioms
of X
1
is contained in the set of axioms of X
2
,which
means X
1
⊆ X
2
.
isHomomorphicTo(X
1
, X
2
) if a homomorphism ex-
ists between the RDF-graph of X
1
and the RDF-
graph of the X
2
.
semanticallyIncludedIn(X
1
, X
2
) if the set of models
of X
1
is contained in the set of models of X
2
. In
other words, if X
2
|= X
1
.
isAConservativeExtentionOf(X
1
, X
2
) , informally, if
syntacticallyIncludedIn(X
2
, X
1
) and all the ax-
ioms entailed by X
1
over the vocabulary of X
2
are
also entailed by X
2
. A more formal definition can
be found in (Ghilardi et al., 2006). The notion of
conservative extension has been used in particular
for ontology modularization (Grau et al., 2007).
import(X
1
, X
2
) if there is an explicit statement in X
1
indicating that it imports X
2
using the owl:imports
primitive. Formally, this means that all the axioms
of X
2
should be considered as contained in X
1
.
The sub-relations of equivalentTo are defined as fol-
lows:
syntacticallyEquivalentTo(X
1
, X
2
) if and only if
SyntacticallyIncludedIn(X
1
, X
2
) and Syntac-
ticallyIncludedIn(X
2
, X
1
).
isIsomorphicTo(X
1
, X
2
) if an isomorphism exists be-
tween the graph of X
1
and the graph of X
2
.
semanticallyEquivalentTo if and only if
semanticallyIncludedIn(X
1
, X
2
) and
semanticallyIncludedIn(X
2
, X
1
).
Finally, following our methodology, we defined the
algebraic properties of each relation
3
and classified
3
Since these are fairly obvious, we do not detail then.
KEOD 2009 - International Conference on Knowledge Engineering and Ontology Development
16
syntacticallyEquivalentTo
equivalentTo
isHomomorphicTosemanticallyIncludedIn
includedIn
isIsomorphicTo
semanticallyEquivalentTo
imports
isAConservativeExtensionOf
isIsomorphicTo
syntacticallyIncludedIn
Figure 2: Taxonomy for includedIn and equivalentTo.
them to create a taxonomic structure relating these re-
lations. This structure is showed in Figure 2
4
.
4.2 similarTo
Ontology similarity has been described as a measure
to assess how close two ontologies are (David and
Euzenat, 2008). Various ways to compute the sim-
ilarity between two ontologies have been described
which are relevant in different application contexts. In
our work, similarTo is used to represent the meaning
of “how an ontology overlap/cover parts of the same
area as interest of another ontology”. Following our
methodology, similarTo has been analyzed and for-
malized at the lexicographic, structural and semantic
level, giving origin to different kinds of similarity re-
lations (see Table 2).
Table 2: Specialization of the similarity relation.
SimilarTo
Semantic semanticallySimilarTo
MappingSimilarTo
Syntactic syntatticallySimilarTo
Lexicographic LexicographicSimilarTo
To define these relations, we need to introduce the
following elements: given two ontologies X
1
and X
2
,
we denote by LC(X
1
, X
2
) the set of axioms of X
1
that
are logical consequences of X
2
and by Voc(X
1
) the vo-
cabulary of X
1
. The following definitions depend on
a threshold T > 0.
semanticallySimilarTo(X
1
, X
2
), if
|LC(X
1
, X
2
)
T
LC(X
2
, X
1
)|
max(|X
1
|, |X
2
|)
≥ T
4
The arrows represent the subPropertyOf relation. For
example, syntacticallyEquivalentTo is a sub property of se-
manticallyIncludedIn.
owlIncompatibleWith
explanationEvolution
syntacticallyEquivalentTo
equivalentTo
isLatterVersionOf isPreviousVersionOf
similarTo
isIsomorphicTo
sematicallyEquivalentTo
syntacticallySimilarTopriorVersion
backwardCompatibleWith conceptualEvolutionOf explanationEvolution
lexicallySimilarTo mappingS imilarTo semanticallySimilarTo
Figure 3: Taxonomy for similarTo. Dashed elements repre-
sent elements from other sections of the ontology.
syntacticallySimilarTo(X
1
, X
2
), if
|X
1
T
X
2
|
max(|X
1
|, |X
2
|)
≥ T
lexicographicallySimilarTo(X
1
, X
2
), if
|Voc(X
1
)
T
Voc(X
2
)|
max(|Voc(X
1
)|, |Voc(X
2
)|)
≥ T
Finally, in addition to the relations defined above,
we also consider a similarity relation that relies on the
existence of an alignment between the two ontologies.
Indeed, mappingSimilarTo is a relation that links
two ontologies X
1
and X
2
if there exists an alignment
from X
1
to X
2
and this alignment covers a substantial
part of the vocabulary of X
1
(i.e., a proportion greater
than a threshold T ). Not that, since alignments can
be unidirectional, mappingSimilarTo differs from
the other similarity functions by not being symmetric.
Finally, we have classified the relations in Table 1
to create the taxonomic structure showed in Figure 3.
4.3 Versioning
Versioning is a temporal relation that concerns the
evolution of an ontology. In (Klein and Fensel, 2001),
the ontology versioning problem has been defined as
the ability to handle changes in ontologies by creating
and managing different variants of it.
An ontology can evolve over time in different di-
rections, e.g. lexicographic, changing the names of
some resources, syntactic, adding or removing ax-
ioms, semantic, changing the definition of some con-
cepts or simply adding or removing axioms. There-
fore, the new ontology could be equivalent or totally
different from the previous one. When we analyze
DOOR - Towards a Formalization of Ontology Relations
17
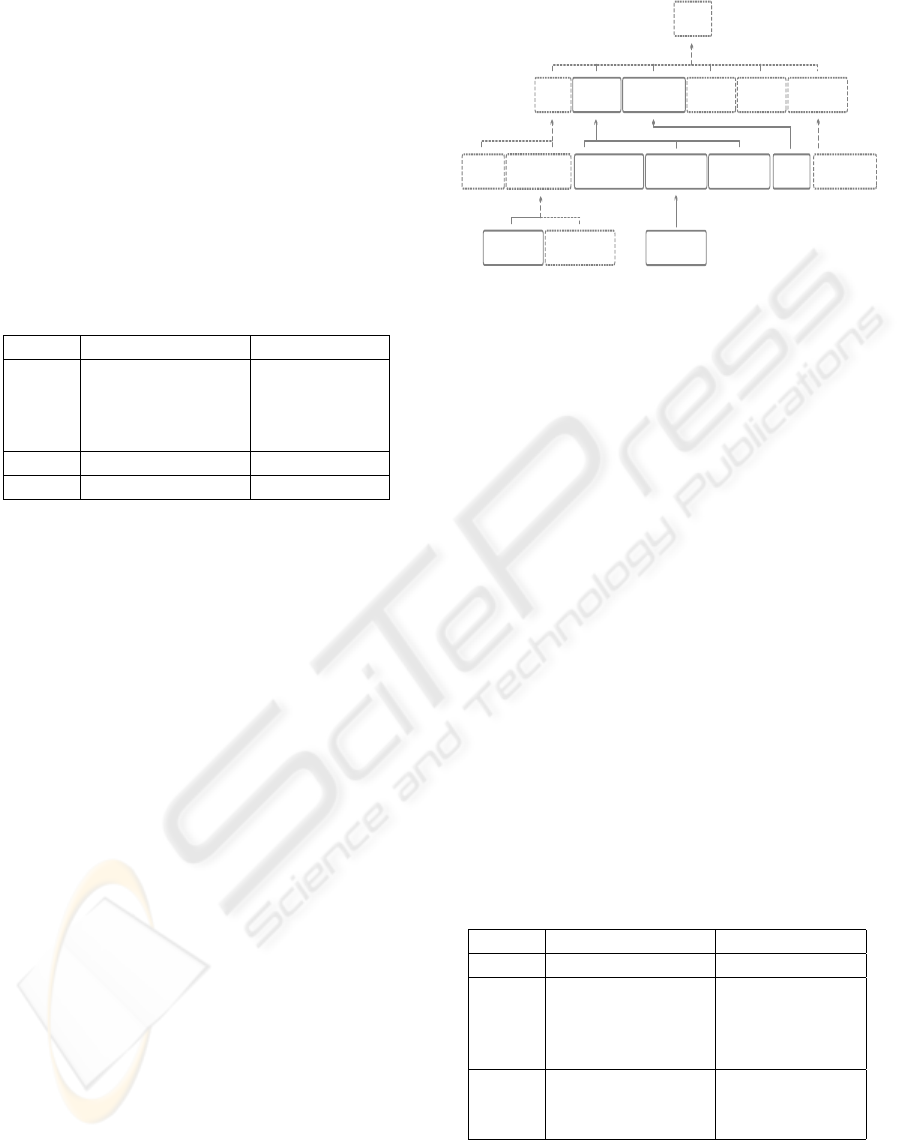
different ways of linking two ontologies by the ver-
sioning relation, the two following sentences are sug-
gested immediately: “X
1
is the previous version of
the X
2
” or “X
2
is the latter version of the X
1
”. These
two typical pieces of knowledge are represented in the
DOOR ontology by the relations isPreviousVersionOf
and its inverse isLatterVersionOf respectively.
Conforming to our methodology, the isPrevi-
ousVersionOf and isLatterVersionOf relations have
been analyzed and formalized, to identify sub-
relations and variants. In Table 3 we summarize the
result of this analysis.
Table 3: Specialization of the versioning relations.
isLatterVersionOf isPreviousVersionOf
Temporal conceptualEvolutionOf priorVersion
explanationEvolutionOf
backwardCompatibleWith
owl:IncompatibleWith
Semantic conceptualEvolutionOf
Syntactic explanationEvolutionOf
According to (Klein et al., 2002; Heflin and Pan.,
2004; Heflin, 2001) the modification of an ontology
can lead to two different types of evolutions: being
a conceptual change, meaning that the model of the
ontology changed, or being an explanation change,
meaning that the modifications happened only at a
syntactic level, without affecting the model of the
ontology. Therefore, we specialized the isLatterVer-
sionOf relation into
conceptualEvolutionOf(X
1
, X
2
) if X
1
is a latter ver-
sion that is not semantically equivalent to X
2
.
explanationEvolutionOf(X
1
, X
2
) if X
1
is a latter ver-
sion that is semantically equivalent to X
2
These two relations will lead to the definition of rules
to infer them from equivalence and other versioning
relations.
In addition, the OWL ontology properties
priorVersion, backwardCompatibleWith and
incompatibleWith represent explicit relations be-
tween versions of ontologies and are included in
DOOR as sub-properties of isLatterVersionO f and
isPreviousVersionO f .
To complete this section of the DOOR ontology,
we can classified the relations in Table 3 as showed in
Figure 4.
Indeed, according to (Klein et al., 2002; Heflin
and Pan., 2004; Heflin, 2001) the modification of an
ontology can lead a new version which is completely
different from the original one. But in practice, by an-
alyzing Watson’s ontology repository, it is almost al-
ways possible establish a similarity between the two
owlIncompatibleWith
explanationEvolution
syntacticallyEquivalentTo
equivalentTo
isLatterVersionOf isPreviousVersionOf
similarTo
isIsomorphicTo
sematicallyEquivalentTo
syntacticallySimilarTopriorVersion
backwardCompatibleWith conceptualEvolutionOf explanationEvolution
lexicallySimilarTo mappingSimilarTo semanticallySimilarTo
Figure 4: Taxonomy for versioning relations.
ontologies, at least at the lexicographic level. Due to
this fact, we chose to consider the versioning relations
to be sub-properties of similarTo, to indicate that two
different versions of the same ontology should, to
some extent, be similar. Moreover, in accordance with
its definition, the explanationEvolutionOf relation is
a sub-property of semanticallyEquivalentTo.
4.4 Agree and Disagree
Based on the formal measures of the agreement
and disagreement between ontologies defined in
(d’Aquin, 2009), we introduce the agreesWith and
disagreesWith relations in DOOR. Informally, the for-
mer holds the general meaning of “to have the same
opinion about something”. In other words, it connects
two ontologies, sharing the same knowledge partially
and is therefore very related to the similarTo and the
equivalentTo relations. The later indicates that the on-
tologies “contradict each other” to a certain extent,
these contradictions appearing at various levels. En-
visaged sub-relations for these two relations are listed
in Table 4.
Table 4: Specialization of agreesWith and disagreesWith.
agreeWith disagreeWith
Temporal backwardCompatibleWith owlIncompatibleWith
Semantic sematicallyEquivalentTo hasDisparateModeling
sematicallySimilarTo incompatibleWith
incoherentWith
incosistentWith
Syntactic syntacticallyEquivalentTo
syntacticallySimilarTo
explanationEvolution
In this Table, all the sub-relations of agreesWith
have already been defined before. We add a few re-
lations to express specific ways for ontologies to dis-
agree, all related to the semantic dimension of the on-
KEOD 2009 - International Conference on Knowledge Engineering and Ontology Development
18
agreesWith
semanticallyEquivalentToBackwardCompatibleWith
explanationEvolution syntacticallyEquivalentTo
syntactiallySimilarTo
semanticallySimilarTo
Figure 5: Taxonomy for the agreement relations.
hasDisparateModelling
incompatibleWith
disagreeWith
incoherentWith inconsistentWith owlIncompatibleWith
Figure 6: Taxonomy for the disagreement relations.
tologies.
incompatibleWith(X
1
, X
2
) if incoherentWith(X
1
, X
2
)
or inconsistentWith(X
1
, X
2
).
incoherentWith According to (Qi and Hunter, 2007)
an ontology X
1
is incoherent if and only if there
is an unsatisfiable concept name in X
1
. Therefore,
two ontologies are incoherent with each other if,
when they are merged, they generate an incoher-
ent result.
inconsistentWith According to (Bell et al., 2007) an
ontology X
1
is inconsistent if it has no model.
Therefore, two ontologies are inconsistent with
each other if, when they are merged, they generate
a inconsistent result.
hasDisparateModeling Two ontologies are consid-
ered to have disparate modeling if they represent
corresponding entities in different ways, e.g. as
an instance in one case and a class in the other.
owl:IncompatibleWith It comes from OWL lan-
guage (Patel-Schneider et al., 2004).
Finally, we have also classified the relations in Table 4
as showed in Figures 5 and 6.
4.5 Other Relations
Analyzing Watson’s ontology repository we found
out that there are many documents which only rep-
resent the TBox of an ontology and others represent-
ing just the ABox. This is captured through the is-
TheSchemaFor relation. isAlignedTo relation links
ontologies for which exists an alignment.
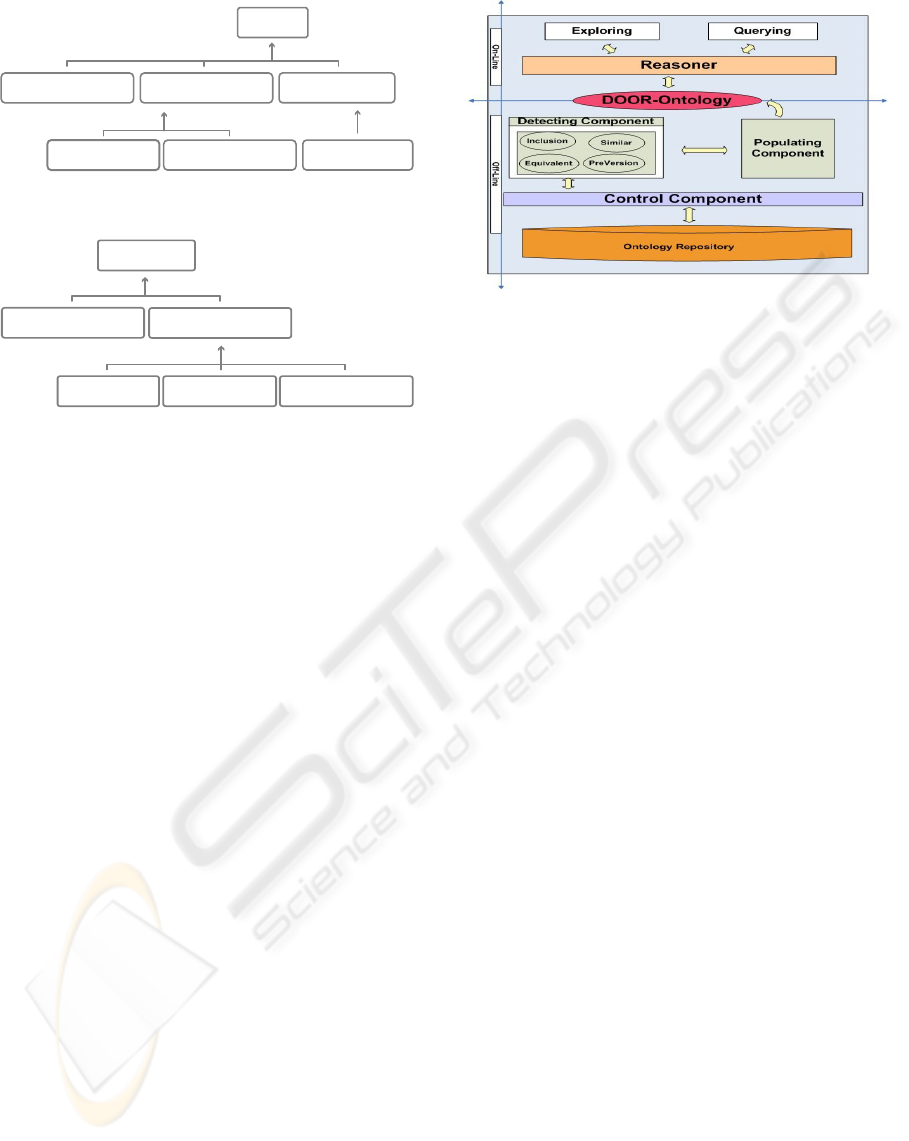
Figure 7: Architecture of the KANNEL framework.
5 KANNEL: AN APPLICATION
FOR THE DOOR ONTOLOGY
In the previous section, we described the DOOR on-
tology in detail. Here we provide a brief overview of
the way it is used in the KANNEL system. KAN-
NEL (Allocca., 2009) is a framework for detecting
and managing ontology relations for large ontology
repositories, such as WATSON. It is an ontology-
based system where the DOOR ontology plays an im-
portant role, providing an explicit representation of
the implicit relations between ontologies. We have
designed an architecture for this framework, as de-
picted in Figure 7. As showed in this figure, the
DOOR Ontology separates the on-line part of the
architecture–providing APIs and services that relies
on a reasoner–from the off-line part–detecting rela-
tions in the repository and populating the ontology.
The offline part is based on three components: the
Control Component (CC), the Detecting Component
(DC) and the Populating Component (PC). As a first
step, the CC selects from the Ontology Repository on-
tologies that need to be evaluated to establish poten-
tial relations. Then, the selected sets of ontologies are
processed by the DC, which contains the main mech-
anisms to discover the possible relations between on-
tologies, relying on the definitions provided in this pa-
per. Finally, the PC populates the semantic structure
with the detected relations. What is obtained is a set
of automatically discovered relations, represented as
part of the DOOR ontology so that the reasoner used
in the system can infer new relations from the onto-
logical and rule based knowledge included in the on-
tology. As such, DOOR provides meta-information
on the ontology repository in KANNEL.
DOOR - Towards a Formalization of Ontology Relations
19

6 CONCLUSIONS
In this paper, general relationships between ontolo-
gies have been examined. In particular, we have cho-
sen to consider well-known relations in the literature,
as well as the ones needed to support the develop-
ment of Semantic Web Applications. To achieve that,
we adapted an ontology building methodology for the
construction of DOOR, an ontology of relations be-
tween ontologies.
This ontology describes relations both from the
point of view of their taxonomic structure and from
the point of view of their formal definitions, provid-
ing the formal properties to describe them as well as
a set of rules to derive complex relations from other
relations.
We also described KANNEL, a framework for de-
tecting and managing ontology relationships for large
ontology repositories. The DOOR ontology plays a
fundamental role in KANNEL, not only to provide an
explicit representation on ontology relations, but also
to supply meta-information that offers several advan-
tages, among which the possibility to reason upon on-
tologies and their relations. This possibility provides
a relevant support for the development of Semantic
Web Applications, which can use the semantic web as
a large-scale knowledge source (d’Aquin et al., 2008).
The first version of the DOOR
ontology is available in OWL at
http://kannel.kmi.open.ac.uk/ontology. The KAN-
NEL framework is currently under development. The
development of DOOR is obviously a continuous
task, which requires a proper assessment of each
version. For this reason, we plan to test and validate
the first version presented here, in particular by
populating it with automatically detected relations
between ontologies in WATSON.
REFERENCES
Allocca., C. (2009). Expliciting semantic relations between
ontologies in large ontology repositories. PhD Sym-
posium, Poster Session, ESWC.
Bell, D., Qi, G., and Liu, W. (2007). Approaches to incon-
sistency handling in description-logic based ontolo-
gies. Proc of the SWWS Conference., 4825/2008.
d’Aquin, M. (2009). Formally measuring agreement and
disagreement in ontologies. 5th K-CAP.
d’Aquin, M., Motta, E., and et al, M. S. (2008). Towards
a new generation of semantic web applications. IEEE
Intell. Sys., 23(3).
d’Aquin, M., Sabou, M., Dzbor, M., Baldassarre, C.,
Gridinoc, L., Angeletou, S., and Mottta, E. (2007).
Watson: A gateway for the semantic web. Poster Ses-
sion at 4th ESWC.
David, J. and Euzenat, J. (2008). Comparison between on-
tology distances (preliminary results). 7th Int. Seman-
tic Web Conference, ISWC.
Gangemi, A., Guarino, N., and Masolo, C. (2001). Under-
standing top-level ontological distinctions.
Gangemi, A., Pisanelli, D. M., and Steve, G. (1999). An
overview of the onions project: Applying ontologies
to the integration of medical terminologies. Technical
report. ITBM-CNR, V. Marx 15, 00137, Roma, Italy.
Ghilardi, S., Lutz, C., and Wolter, F. (2006). Did I damage
my ontology? a case for conservative extensions in
description logics. In 10th Inter. Conf. (KR), pages
187–197. AAAI Press.
Grau, B. C., Horrocks, I., Kazakov, Y., and Sattler, U.
(2007). Just the right amount: Extracting modules
from ontologies. In WWW, pages 717–726. ACM.
Heflin, J. (2001). Towards the semantic web: Knowledge
representation in a dynamic, distributed environment.
Ph.D. Thesis, University of Maryland, 2001.
Heflin, J. and Pan., Z. (2004). A model theoretic semantics
for ontology versioning. 3th ISWC, Hiroshima, Japan,
LNCS 3298 Springer, pages 62–76.
Klein, M. and Fensel, D. (2001). Ontology versioning on
the semantic web. Proc. of the Inter. Semantic Web
Working Symposium (SWWS), pages 75–91.
Klein, M., Fensel, D., Kiryakov, A., and Ognyanov, D.
(2002). Ontology versioning and change detection on
the web. 13th EKAW02, pages 197–212.
Kleshchev, A. and Artemjeva, I. (2005). An analysis of
some relations among domain ontologies. Int. Journal
on Inf. Theories and Appl, 12:85–93.
Konev, B., C.Lutz, D.Walther, and F.Wolter (2008). Cex and
mex: Logical diff and logic-based module extraction
in a fragment of owl. Liverpool Uni and TU Dresden.
Maedche, A. and Staab, S. (2002). Comparing ontologies-
similarity measures and a comparison study. Proc. of
EKAW-2002.
Noy, N. F. and Musen, M. A. (2002). Promptdiff: A fixed-
point algorithm for comparing ontology versions. 18th
National Conf. on Artificial Intelligence (AAAI).
Patel-Schneider, P. F., Hayes, P., and Horrocks, I. (2004).
Owl web ontology language semantics and abstract
syntax. W3C Recommendation.
Qi, G. and Hunter, A. (2007). Measuring incoherence in
description logic-based ontologies. Proc of the Int.
Sem. Web Conference., 4825/2008:381–394.
Volkel, M. (2006). D2.3.3.v2 SemVersion Versioning RDF
and Ontologies. EU-IST Network of Excellence (NoE)
IST-2004-507482 KWEB.
KEOD 2009 - International Conference on Knowledge Engineering and Ontology Development
20
