ON ADAPTIVE MODELING OF NONLINEAR EPISODIC

REGIONS IN KSE-100 INDEX RETURNS

Rosheena Siddiqi and Syed Nasir Danial

Bahria University, Karachi, Pakistan

Keywords: Financial forecasting, Bicorrelation test, Transient nonlinearity, Neural network.

Abstract: This paper employs the Hinich portmanteau bicorrelation test with the windowed testing method to identify

nonlinear behavior in the rate of returns series for Karachi Stock Exchange indices. The stock returns series

can be described to be comprising of few brief phases of highly significant nonlinearity, followed by long

phases in which the returns follow a pure noise process. It has been identified that major political and

economic events have contributed to the short bursts of nonlinear behavior in the returns series. Finally,

these periods of nonlinear behavior are used to predict the behavior of the rest of the regions using a

feedforward neural network and dynamic neural network with Bayesian Regularization Learning. The

dynamic neural network outperforms the traditional feedforward networks because Bayesian regularization

learning method is used to reduce the training epochs. The time-series generating process is found to closely

resemble a white noise process with weak dependence on value at lag one.

1 INTRODUCTION

The nonlinear behavior of financial time series data

has intrigued researchers for more than a decade and

it has seen further growth in recent years. Among

the factors, which induce nonlinearity, are

difficulties in executing arbitrage transactions,

market imperfections, irrational behavior of

investors, diversity of belief in agents, and

heterogeneity of objectives with investors. Research

has produced encouraging results, with more and

more empirical evidence emerged to suggest that

nonlinearity is a universal phenomenon (Kantz and

Schreiber 1997). This has received a wide empirical

support across different financial markets. However,

presence of nonlinearity in stock exchange index,

returns, or in the data which shows direction of

stocks, forms serious consequences for the well

known Efficient Market Hypothesis (EMH) of

finance, which states that markets are efficient in

that opportunities for profit are discovered so

quickly that they cease to be opportunities. EMH

effectively states that no system can continually beat

the market because if a system becomes public

everyone will use it thus negating its potential gain.

A direct corollary of this hypothesis is that stock

prices form a stochastic process ⎯ a Markovian

process of certain order ⎯ and that any profit

derived from timing the market are due entirely to

chance.

Now detecting nonlinearity, in general, is

considered a difficult problem in dynamical systems

theory, or nonlinear time-series analysis, to be

specific. There are several standard ways to assess

nonlinearity in a given time-series data, e.g.,

determining estimates of intrinsic dimension, such as

box-counting and correlation dimension (using

Grassberger and Procaccia (1983), (1983a)), finding

the maximum Lyapunov exponent, etc., see (Kantz

and Schreiber 1997). All these estimates are

invariants and can only be estimated in a phase-

space of some appropriate embedding dimension.

Moreover, a possible attractor in which to confine

our attention for discovering nonlinear behavior

requires abundance of data points, N. Methods

which deal with estimation of invariant quantities in

a nonlinear setting are not only difficult for

application purpose but also that they require huge

amount of data. There are several criteria one can

exploit to check for the fulfillment of this condition

(we refer to Kantz and Schreiber (1997) for details

about such criteria). In general, an attractor with a

high (unknown) dimension needs larger number of

data points for the estimation of its dimension as

compared to that whose dimension is low.

402

Siddiqi R. and Danial S. (2009).

ON ADAPTIVE MODELING OF NONLINEAR EPISODIC REGIONS IN KSE-100 INDEX RETURNS .

In Proceedings of the International Joint Conference on Computational Intelligence, pages 402-407

DOI: 10.5220/0002276804020407

 SciTePress

Besides the difficulties of employing standard

nonlinear time-series methods such as those

discussed in Barnett et al. (1996), there are some

statistical techniques, which are helpful in deciding

if a given financial time-series is nonlinear. Lim and

Hinch (2005) argue that the detected nonlinear

behavior, i.e., the linear and nonlinear serial

dependence which can be estimated by computing

portmanteau correlation, bicorrelation and

tricorrelation, is episodic in that there are long

periods of pure noise process, only to be interrupted

by relatively few brief episodes of highly significant

non-linearity. Such nonlinearities may be detected

by employing a windowing approach proposed by

Hinich and Patterson (1995) to detect major political

and economic events that may have contributed to

the short burst of non-linear dependencies. Their

study advocated a form of event studies that is data

dependent to determine endogenously those events

that trigger non-linear market reactions. We use this

technique to find out regions in our data where

nonlinearity is significant; political events are listed

which may be responsible for such a behavior.

Based on this information, we construct neural

network models for each frame. It is further

observed that inside a given region the forecast error

is found to be less as compared to what is observed

when we forecast values outside the region. This

finding is of utmost importance to us because it

suggests insignificance of global models.

Section 2 explains some of the previous work. In

section 3, we give basic definitions of the concepts

being used in this analysis. Section 4 presents our

computations regarding windowing approach. We

also construct neural network models of our

computed frames. Finally, section 5 opens with a

discussion and concludes the entire present work.

2 PREVIOUS WORK

The Karachi Stock Exchange (KSE-100 index) is the

main stock exchange in Pakistan. In a recent study

by Danial et al. (2008), the authors have tested the

daily stock returns of the entire history of KSE-100

index against nonlinearity. A nonlinear dynamical

system invariant, viz., correlation dimension is

attempted to be computed but they have concluded

that correlation dimension can not be estimated due

to either insufficient data or insufficient information

content within available data so as to be framed as a

dynamical system. However, Danial et al. (2008)

demonstrates modeling of KSE-100 index returns

using feedforward neural network with a comparison

to ARMA/ARIMA modeling. In Burni, Jilani and

Ardil (2004), the author use neural network to model

KSE-100 direction of index data. Here only very

short time series is used for modeling purpose in

contrast with the work of Danial et al. (2008).

Antoniou, Ergul, and Holmes (1997) and Sarantis

(2001) list several possible factors which might

induce nonlinearity in stock returns.

Much of the earlier evidence of the presence of

nonlinearity was drawn from stock markets of

developed countries. Hinich and Patterson (1985)

establish the presence of nonlinear non-Gaussian

process generating daily stock returns by estimating

a bispectrum of time series data of fifteen common

stocks chosen at random from the set of stocks listed

continuously on the New York Stock Exchange and

American Stock Exchange, and describe a test of

nonlinearity based on skewness. Similar findings

regarding nonlinearity observed in Latin America

and UK are respectively reported by Bonilla,

Romero-Meza, and Hinich (2006), Abhyankar,

Copeland and Wong (1995) and Opong et al. (1999).

However in recent years, more and more evidence of

nonlinearity from emerging stock markets are

documented by Brooks and Hinich (1998),

Ammermann and Patterson (2003), Lim, Hinich,

Liew (2003), Lim and Hinich (2005, 2005a). In

particular, Hinich and Patterson (1985), discuss the

parameter instability of GARCH models and the

transient nature of ARCH effects. It has been shown

that the GARCH model cannot be considered a full

representation of the process generating financial

market returns. In particular, the GARCH models

fails to capture the time-varying nature of market

returns, and treats coefficients as fixed and being

drawn from only one regime.

In all these aforementioned studies, the detected

nonlinear behavior is also episodic in that there were

long periods of pure noise process, only to be

interspersed with relatively few brief episodes of

highly significant nonlinearity as shown by Wild,

Hinich and Foster (2008).

3 FUNDAMENTAL CONCEPTS

3.1 The Portmanteau Bicorrelation

Tests

The ‘windowing’ approach and the bicorrelation test

statistic proposed in Hinich and Patterson (1995)

(denoted as H statistic) are briefly described in this

section. Let there be a sequence {y(t)} which

denotes the sampled data process, where the time

ON ADAPTIVE MODELING OF NONLINEAR EPISODIC REGIONS IN KSE-100 INDEX RETURNS

403

unit, t, is an integer. The test procedure employs

non-overlapped data window, thus if n is the

window length, then k-th window is {y(t

), y(t

+1),

…, y(t

+n–1)}. The next non-overlapped window is

{y(t

k+1

), y(t

k+1

+1), …, y(t

k+1

+n−1)}, where t

+1 =

. The null hypothesis for each window is that y(t)

are realizations of a stationary pure noise process

that has zero bi-covariance.

We state without proof and derivation that the H

statistic is defined as:

  



















(1)

χ













Where























(2)

and



















































(3)

where Z(t) are the standardized observations,

obtained by subtracting the sample mean of the

window and dividing by its standard deviation. The

number of lags L is specified as L= n

with 0 < b <

0.5, where b is a parameter under the choice of the

user. Based on the results of Monte Carlo

simulations, Hinich and Patterson (1995)

recommended the use of b = 0.4 in order to

maximize the power of the test while ensuring a

valid approximation to the asymptotic theory even

when n is small. In this test procedure, a window is

significant if the H statistic rejects the null of pure

noise at the specified threshold level.

3.2 Neural Network

Parameterized nonlinear maps, capable of

approximating arbitrary continuous functions over

compact domains are known as neural networks. It

has been proven by Cybenko (1989) and Hornik,

Stinchcombe, & White (1989) that any continuous

mapping over a compact domain can be estimated as

accurately as required by a feedforward neural

network with a single hidden layer.

In the context of neural network literature, the

term neuron refers to an operator that maps ℜ

→ℜ

and can be illustrated by the equation



















(4)

where U

= [u

, u

,… u

] is the input vector, W

, w

,… w

] is referred to as the weight vector of

the neuron, and w

is the bias. Г(.) is a monotone

continuous function such that Г(.):ℜ→(−1, 1). The

function Г(.) is commonly called a ‘sigmoidal

function’; tanh(.), and (1+exp(−(.)))

−1

are some

widely used examples. The neurons can be arranged

in a variety of layered architecture with

layers l = 0,

1, … L, such as, feedforward, dynamic, ARX

networks, Vector Quantization networks, etc. A

neural network, as defined above, represents a

specific family of parameterized maps. If there are

input elements and n

output elements, the

network defines a continuous mapping

NN:













4 ANALYSIS OF KSE-100 INDEX

RETURNS

The present work is an attempt for analyzing

economic conditions for the current fiscal decade

when Pakistan has undergone serious changes in its

financial and political policies. Literature describing

such policies and their impact on economy abounds.

In a sense, the purpose of this work is three-fold;

first, we attempt to find out regions of significant

transient nonlinearity. Second, we use this

information to construct models which may be used

for short-term forecasting. Finally, we try to find out

those events which might have been the reason for

the observed transient nonlinearity.

A time-series T is obtained using {y

}

1≤i≤2195

= log(p

i−1

), where p

represents the i

day stock index,

from October ′99 to August ′08. The autocorrelation

function of T shows clearly that the series is first-

order stationary. The partial autocorrelation function

(PACF) plot of T reveals significant peak at lag 1,

thus we compute H statistic for the residuals

obtained after fitting an autoregressive model of unit

order, AR(1). The minimum AICC Yule-Walker

equation for the series T is given here as under:





 







(5)

The value of AICC statistic is –12988.8. Based on

this information, the residuals of the series T are

used to construct frames each of length thirty as

described in the previous section. Our results show

IJCCI 2009 - International Joint Conference on Computational Intelligence

404

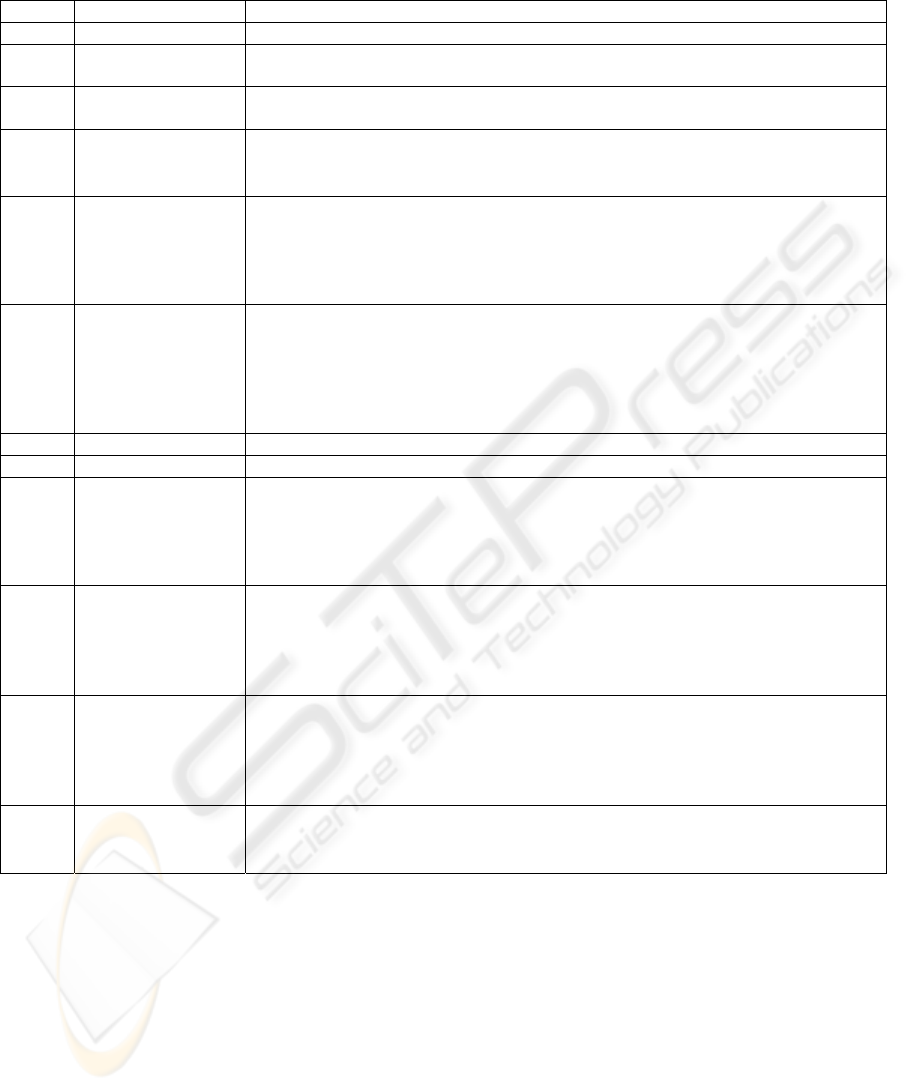
Table 1: Significant Frames with nonlinear behavior along with Major Events; Total Number of windows: 74; Significant H

windows: 12 (16.2%).

Frame Date Major Events

11/16/99 - 12/28/99 A month after Military Coup (12

October 1999)

3/21/01 - 5/7/01 Ex-President Rafiq Tarar resigns, Ex- President Pervez Musharraf takes over ( a

month after the frame – this does not induce nonlinearity)

6/10/03 - 7/21/03 Khalid Sheikh Mahmood (suspected mastermind of 9/11) arrested (3 months before

the nonlinear region)

4/15/04 - 5/27/04

• National Security Council Bill passed

• EU decides to improve trade with Pakistan

• Pakistan is back in Commonwealth

12/31/04 - 2/14/05

• Tsunami hits far-eastern countries

• Ex-President Pervez Musharraf decides to keep his post as army

• Pakistan Army opens fire on insurgents in Baluchistan, in the first armed

uprising since General Rahimuddin Khan’s stabilization of the province in 1978

(A month after this nonlinear region)

9/16/05 - 10/27/05

• Bombs exploded in KFC and McDonalds in Karachi

• October 2005 Earthquake killing over 175, 000 people in Northern regions of

Pakistan

• Ex President Pervez Musharraf shakes hands with Israeli Prime Minister Ariel

Sharon and later addresses American Jewish Society later in the month, creating

a row

6/16/06 - 7/27/06 Waziristan war heats up (suicide bombings escalated)

12/13/06 - 1/26/07 Waziristan War (military retaliated)

6/11/07 - 7/20/07

• Operation on Lal Masjid (Islamabad)

• Torrential rains in Sindh, Balochistan causing flood

• Talks between Ex-President Pervez Musharraf and opposition leader Ex-Prime

Minister (late ) Benazir Bhutto take place in Dubai causing speculations of

potential coalition

10/22/07 - 12/3/07

• Right after first assassination attempt on Ex-Prime Minister (late ) Benazir

Bhutto 18th Oct 2007

• Emergency imposed 3

Nov 2007

• Ex-Prime Minister Nawaz Sharif makes a failed attempt to return to Pakistan

• Ex-President Pervez Musharraf stands down as the head of Pakistan army

12/4/07 - 1/18/08

• Emergency lifted by Ex-President Pervez Musharraf

• Ex-Prime Minister (late ) Benazir Bhutto’s assassinated on 27th Dec 2007, riots

• Rumors of assassination of Ex-President Pervez Musharraf

• General Elections delayed till February

• General Elections held (exactly a month after the nonlinear region ends)

4/17/08 - 5/29/08

• Changing policy towards militants, talks with local Taleban

• Ministers of PML(N) resign from Federal government

• Lawyers movement continue

that out of around seventy three frames twelve are

those in which significant nonlinearity is observed

(see Table 1). The frames which are subjected to

further analysis are those which are taken as

common after estimating H statistic of residuals of

AR(1) and AR(9) models, because the PACF at lag

1 and 9 show peaks beyond statistical significance.

Assuming that F

represents the i

frame with i = {1,

2, …, m=12} containing values from T such that

individual frame F

takes consecutive values from T

but frames F

and F

with i ≠ j do not necessarily

come adjacent to each other in T. Thus, we can write

= {y

, y

, …, y

}, F

= {y

, y

, …,

}, and in general F

= {y

, y

, …, y

where k is the frame length which is 30 in our case.

Each of these sets F

is used as input to a

feedforward neural network with lag 1. Obviously,

each F

is divided into training, validation and testing

sets for modeling with neural network. We use

gradient descent backpropagation algorithm for

training with varying number of neurons and hidden

layers. This way, we have come across having

several neural network models for each of the frame

, however, for brevity, Table 1 describes only

those neural networks which traced the behavior of

input data comparatively well. On average, all the

ON ADAPTIVE MODELING OF NONLINEAR EPISODIC REGIONS IN KSE-100 INDEX RETURNS

405

Table 2: The results of NN-modeling.

Feedforward - Backpropagation Dynamic Network, Bayesian regularization

Frame MSE Neurons Epochs SSE Neurons Epochs Forecast Original

Day-1 Day-2 Day-1 Day-2

3.65×10

−4

1 208

3.52×10

−

4 11 0.012 0.007 0.021 0.0336

5.56×10

−5

1 34

1.08×10

−

4 10 0.0051,

−

0.0049 −0.0133 −0.0079

1.24×10

−4

1 1500

4.14×10

−

4 9 0.004 0.003

−0.007

0.013

9.77×10

−4

1 81

1.13×10

−

4 47

−

0.001

−

0.006

0.0047

−0.0009

9.93×10

−4

4 316

1.59×10

−

4 9 0.014 0.0063 0.008 0.014

9.74×10

−4

1 78

1.8×10

−

4 104 0.00994 0.0051

−0.0085

0.0227

9.91×10

−4

3 105

6.3×10

−

4 8 0.0084

−

0.0038 −0.0074

0.014

9.70×10

−4

1 104

1.6×10

−

4 9 0.0067 0.0091 0.015 0.0067

9.43×10

−4

1 16

1.05×10

−

4 10 0.0119

−

0.0030

0.0228

−0.0079

9.65×10

−4

1 78

3.39×10

−

4 13

−

0.0054

−

0.0066

0.0081 0.0072

9.99×10

−4

1 145

2.5×10

−

4 9 0.0146

−

0.0032 −0.0066

0.0020

9.77×10

−4

1 86

2.0×10

−

4 9

−

0.0016

−

0.0084

0.0123 0.0160

neural networks are found to have mean square error

~ 10

–4

. To improve the Day-1 and Day-2 out-of-

sample forecast we employ a dynamic neural

network with Bayesian Regularization Learning.

This has greatly improved our results and at several

points we find a very little difference between the

observed and the forecasted values. Besides there

are deviations of long magnitude which are probably

due to less

amount of training data, only around 10

points in each frame.

5 CONCLUSIONS

The Hurst Exponent (Hu) of the series T is found to

be 0.6 which shows a slight effect of long memory

with persistence but the process, in general, may

also be considered as a first-order autoregressive

process. However, the regression is contributed by

only a very less amount of previous value (see

equation 5), and as a whole the process should be

treated to be governed by white noise. And that is

the reason why we obtain the Hu close to 0.5, on

contrary to 1.0.

The windowing-approach is found to give

satisfactory results as the most effective and

significant events (see Table 2) that have affected

the country’s economical growth, political stability

and international relations happened during our

detected nonlinear regions.

The forecasting results obtained after applying a

dynamic neural network with Bayesian

regularization learning supersedes the conventional

feedforward-backpropagation network. We think

that the major obstacle against good forecasting is

the amount of data which is limited to ten in a single

frame due to the frame length, or actually the length

of the transient period in which nonlinearity is

significant. Finding the global parameters of the

dynamics of the involved process should be an

interesting problem to attempt.

REFERENCES

Kantz, H & Schreiber, T 1997, Nonlinear time series

analysis, University Press, Cambridge

Grassberger, P, & Procaccia, I 1983, ‘Measuring the

strangeness of strange attractors’. Physica D, vol. 9,

pp. 189.

Grassberger, P. & Procaccia, I. 1983a, Characterization of

strange attractors. Phys. Rev. Lett., vol. 50, pp. 346.

Barnett, W.A., Gallant, A.R., Hinich, M.J., Jungeilges,

J.A., Kaplan, D.T. & Jensen, M.J. 1996, An

Experimental Design to Compare Tests of

Nonlinearity and Chaos, Nonlinear Dynamics and

Economics, in Proceedings of The Tenth International

Symposium in Economic Theory and Econometrics,

Eds. W. A. Barnett, A.P. Kirman, and M. Salmon,

Cambridge University Press, New York, NY

Lim, K.P. & Hinich, M. J. 2005, Cross-temporal

universality of non-linear dependencies in Asian stock

markets, Economics Bulletin vol. 7, no. 1, pp. 1-6.

Hinich, M. J. & Patterson D. M. 1995, Detecting epochs of

transient dependence in white noise. Mimeo,

University of Texas at Austin.

Danial, S. N., Noor, S. R., Usmani, B. A., & Zaidi, S.J.H.

2008, A Dynamical System and Neural Network

Perspective of Karachi Stock Exchange Returns. in

International Multi – Topic Conference IMTIC 2008 ,

Dr. M. Akbar Hussain, Abdul Qadeer Khan Rajput,

Bhawani Shankar Chowdhry and Quintin Gee (Eds.),

Mehran University Jamshoro, Pakistan. April 11-12,

2008. Revised Selected Papers. Wireless Networks,

Information Processing and Systems, Communications

in Computer and Information Science vol. 20, pp. 88-

99, Springer-Verlag, Heidelberg. For Online version:

IJCCI 2009 - International Joint Conference on Computational Intelligence

406

http://www.springerlink.com/content/978-3-540-

89852-8?sortorder=asc&p_o=10

Burni, S. M. A., Jilani, T. A. & Ardil C. 2004, Levenberg-

Marquardt Algorithm for Karachi Stock Exchange

Share Rates Forecasting. Proceedings of World

Academy of Science, Engineering and Technology vol.

3, (ISSN1307-6884).

Antoniou, A., Ergul N. & Holmes P. 1997, Market

efficiency, thin trading and non-linear behavior:

evidence from an emerging market. European

Financial Management, vol. 3, no. 2, pp. 175-190.

Sarantis, N. 2001, Nonlinearities, cyclical behaviour and

predictability in stock markets: international evidence.

International Journal of Forecasting, vol. 17, pp. 459-

482.

Hinich, M.J. & Patterson, D. M. 1985, Evidence of

nonlinearity in daily stock returns. Journal of Business

and Economic Statistics, vol. 3, pp. 69-77.

Bonilla, C. A., Romero-Meza, R. & Hinich, M. J. 2006,

Episodic nonlinearity in Latin American stock market

indices. Applied Economics Letters, vol. 13, no. 3, pp.

195-199.

Abhyankar, A.H., Copeland L. S. & Wong W. 1995,

Nonlinear dynamics in real-time equity market

indices: evidence from the United Kingdom.

Economic Journal, vol. 105, pp. 864-880.

Opong, K.K., Mulholland, G., Fox, A. F. & Farahmand,

K. 1999, The behavior of some UK equity indices: an

application of Hurst and BDS tests. Journal of

Empirical Finance, vol. 6, pp. 267-282.

Brooks, C. & Hinich M. J. 1998, Episodic nonstationarity

in exchange rates. Applied Economics Letters, vol. 5,

pp. 719-722.

Ammermann, P.A. & Patterson D. M. 2003, The cross-

sectional and cross-temporal universality of nonlinear

serial dependencies: evidence from world stock

indices and the Taiwan Stock Exchange. Pacific-Basin

Finance Journal, vol. 11, pp. 175-195.

Lim, K.P., Hinich, M. J. & Liew, V. K. S 2003, Episodic

non-linearity and non-stationarity in ASEAN

exchange rates returns series. Labuan Bulletin of

International Business andFinance, vol. 1, no. 2, pp.

79-93.

Lim, K.P. & Hinich, M. J. 2005, Cross−temporal

universality of non−linear dependencies in Asian stock

markets. Economics Bulletin, vol. 7, no. 1, pp. 1

−6

Lim, K.P. & Hinich, M. J. 2005a, Non−linear Market

Behavior: Events Detection in the Malaysian Stock

Market. Economics Bulletin, vol. 7, no. 6, pp. 1−5

Wild, P., Hinich, M. J., Foster, J. 2008, Are Daily and

Weekly Load and Spot Price Dynamics in Australia’s

National Electricity Market Governed by Episodic

Nonlinearity, Discussion Paper, University of

Queensland, pp. 6-10.

Cybenko, G. (1989), Approximation by Supervisions of a

Sigmoidal Function. Mathematics of Control, Signals,

and Sys., vol. 2, pp. 303–314.

Hornik, K, Stinchcombe, M, & White, H 1989, Multilayer

feed-forward networks are universal approximators,

Neural Net., vol. 2, pp. 359–36

ON ADAPTIVE MODELING OF NONLINEAR EPISODIC REGIONS IN KSE-100 INDEX RETURNS

407