THE UPHILL BATTLE OF ANT PROGRAMMING VS. GENETIC
PROGRAMMING
Amirali Salehi-Abari and Tony White
School of Computer Science, Carleton University, Ottawa, Canada
Keywords:
Automatic programming, Genetic programming, Ant programming, Enhanced generalized ant Programming.
Abstract:
Ant programming has been proposed as an alternative to Genetic Programming (GP) for the automated pro-
duction of computer programs. Generalized Ant Programming (GAP) – an automated programming technique
derived from principles of swarm intelligence – has shown promise in solving symbolic regression and other
hard problems. Enhanced Generalized Ant Programming (EGAP) has improved upon the performance of
GAP; however, a comparison with GP has not been performed. This paper compares EGAP and GP on 3
well-known tasks: Quartic symbolic regression, multiplexer and an ant trail problem. When comparing EGAP
and GP, GP is found to be statistically superior to EGAP. An analysis of the evolving program populations
shows that EGAP suffers from premature diversity loss.
1 INTRODUCTION
Automatic programming is an active research area
that has been stimulated by the Genetic Programming
(GP) technique. In automatic programming, the goal
of the desired program is first specified; then, based
upon this goal, programs are generated according to
an algorithm and tested to demonstrate to what ex-
tent they satisfy the desired goal. Genetic program-
ming (GP) was proposed by Koza (Koza, 1992; Koza,
1994; Koza et al., 1999). GP utilizes an idea similar to
that of a genetic algorithm (GA) but with representa-
tional and operator differences. GP represents genes
in a tree structure as opposed to an array of numbers
typically used in a GA. Miller and Thomson (Miller
and Thomson, 2000) introduced a form of GP called
Cartesian Genetic Programming, which uses directed
graphs to represent programs rather than trees.
While search algorithms inspired by evolution
have demonstrated considerable utility, other learn-
ing models are attracting increasing interest. One
model of social learning recently attracting increas-
ing attention is Swarm Intelligence (SI). There are
two main classes of algorithm in this field: ant colony
system (ACS) and particle swarm optimization (PSO)
(Bonabeau et al., 1999). The former is inspired by
the collaborative behavior of ants while the latter is
derived from the flocking behavior of birds and fish.
ACS and PSO have been used in Automatic Pro-
gramming. O’Neill and Ryan present an automatic
programming model called Grammatical Swarm (GS)
(O’Neill and Brabazon, 2006). In this model, each
particle or real value vector represents choices of pro-
gram construction rules specified as production rules
of a Backus-Naur Form (BNF) grammar. In other
words, each particle shows the sequence of rule num-
bers by applying which a program can be constructed
from the starting symbol of the grammar.
Other researchers have used ACS for automatic
programming. Roux and Fonlupt (Roux and Fonlupt,
2000) use randomly generated tree-based programs.
A table of program elements and corresponding val-
ues of pheromone for these elements is stored at each
node. Each ant builds and modifies the programs ac-
cording to the quantity of an element’s pheromone at
each node.
Boryczka and Czech have presented two other
models of Ant programming (Boryczka and Czech,
2002; Boryczka, 2002). They used their model only
for symbolic regression. In the first approach - called
the expression approach - they search for an approx-
imating function in the form of an arithmetic expres-
sion written in Polish (Prefix) notation. In the second
approach, the desired approximating approach is built
as a sequence of assignment instructions which evalu-
ates the function. That is, there is a set of assignment
instruction defined by the user; each of these assign-
ment instructions is placed on a node of graph. Then,
171
Salehi-Abari A. and White T. (2009).
THE UPHILL BATTLE OF ANT PROGRAMMING VS. GENETIC PROGRAMMING.
In Proceedings of the International Joint Conference on Computational Intelligence, pages 171-176
DOI: 10.5220/0002277401710176
Copyright
c
 SciTePress

ants build their program by selecting the sequence of
these instructions while passing through the graph.
Keber and Schuster offer a new AP model using
a context-free grammar and an ant colony system,
called Generalized Ant Programming (GAP) (Keber
and Schuster, 2002). The lack of a termination con-
dition for generating the path by each ant and gen-
erating paths with non-terminal components in GAP
motivated Salehi-Abari and White (Salehi-Abari and
White, 2008) to introduce Enhanced Generalized Ant
Programming (EGAP). EGAP, by providing a heuris-
tic for path termination inspired by building construc-
tion and a novel pheromone placement algorithm ad-
dresses the weaknesses of GAP and demonstrates a
statistically significant improvement.
Despite the existence of numerous swarm-based
automatic programming techniques, especially ant
programming, in the literature, they are rarely com-
pared to traditional simple genetic programming. We
have chosen EGAP as a representative of the ant pro-
gramming approach because of its generality and per-
formance to compare with GP. Furthermore, EGAP
has been shown to be superior to GAP in the experi-
mental domains used in this paper.
The main contribution of this paper is the com-
parison of genetic programming to EGAP, a repre-
sentative of the ant programming approach. We have
compared the performance of EGAP with GAP on 3
well-known problems: Quartic symbolic regression,
multiplexer and Santa Fe ant trail. The results ob-
tained demonstrate that GP has statistically significant
superior performance. We have shown through ex-
periments that EGAP suffers premature convergence
because of generating excessive numbers of identical
solutions. We do not claim here that by comparing
GP with EGAP that GP performance is superior to
that of all ant-based programming techniques. Rather,
we simply show that EGAP faces several challenges
suitable for study with further research.
The remainder of the paper is structured as fol-
lows. In sections 2 and 3, the GP and EGAP algo-
rithms are summarized respectively. Section 4 details
the experimental approach adopted and results. Fi-
nally, Section 5 provides conclusions and opportuni-
ties for future work.
2 GENETIC PROGRAMMING
Genetic programming represents programs in a tree
structure (Koza, 1992; Koza, 1994; Koza et al., 1999).
More specifically, the tree is composed of functions
which are the internal nodes and terminals which are
the leaves. The set of terminals includes variables
(e.g., X) and constant numbers. An example of a pro-
gram tree is shown in Figure 1.
+
X3X
Sin
*
Figure 1: GP Program tree structure.
The program shown in Figure 1 represents 3X +
sin(X). It should be noted that some functions may
havetwo parametersand some have only one. In other
words, the arity of a given function within the func-
tion set is variable (e.g., 2 for + and 1 for sin) and
varies from one domain to another.
The basic premise of GP is to produce a random
initial population of program trees, and then apply ge-
netic operators such as crossover and mutation in each
generation. First, the fitness of all programs is cal-
culated. Then, programs are selected proportional to
their fitness by the use of a tournament (or other) se-
lection algorithm. If the total population is N, then k
random programs are selected with replacement. The
program with the highest fitness goes into the mating
pool. The next step is to crossover pairs of programs
in the mating pool by taking and swapping subtrees
from each program. This produces two new children.
When the process is complete, a new generation is
produced. We use the same process for generating so-
lutions for a fixed number of generations.
3 EGAP
3.1 Introduction
Enhanced Generalized Ant Programming (EGAP),
introduced by Salehi-Abari and White (Salehi-Abari
and White, 2008), is a new method of Automatic Pro-
gramming. EGAP is an approach designed to gen-
erate computer programs by simulating the behavior
of ant colonies.When ants forage for food they lay
pheromone on the ground that affects the choices they
make. Ants have a tendency to choose steps that have
a high concentration of pheromone.
3.2 Methodology
In EGAP and GAP, L (G ) is the programming lan-
guage in which an automatically generated program
IJCCI 2009 - International Joint Conference on Computational Intelligence
172

is written and it is specified by the context-free gram-
mar G = (N , T erm, R , S ). In other words, L (G )
is a set of all expressions that can be produced from
a start symbol S under application of R rules. Note
that, N is a set of non-terminal symbols, and T erm
is a finite set of terminal symbols. Thus,
L ( G ) = { P | S ⇒ P ∧ P ∈ T erm
∗
} (1)
Where T erm
∗
represents the set of all expres-
sions that can be produced from the T erm symbol
set. Given the grammar G , a derivation of expres-
sion P ∈ L ( G ) consists of a sequence of t
1
,t
2
, ... ,t
p
of terminal symbols generated from the sequence of
derivation steps.
Assume the following G
G = (N = {S, T,F},
T erm = {a,+,∗,(,)} ,
R = {S → S+ T |T, T → T ∗ F| F,F → (S) | a},
S = {S})
Each derivation in this grammar represents a
simple arithmetic expression including the symbols
a,+,∗,(, and ). The simple derivation of this gram-
mar is presented below:
S ⇒ S + T ⇒ T + T ⇒ F + T ⇒ a + T ⇒ a+
T ∗ F ⇒ a+ F ∗ F ⇒ a+ a ∗ F ⇒ a+ a∗ a
In EGAP, L (G ) is the search space of all possi-
ble expressions (programs) that can be generated by
the grammar G . Therefore, P ∈ L (G ), which is an
expression (a program), is a path visited by one ant.
In EGAP, the total amount of pheromone ant k
places on the trail is:
Θ
k
= f(rank(k)). L
k
(t, p) (2)
Where L
k
(t, p) is the value of the objective function
obtained by ant k at time t and f(rank(k)) is a factor
that depends on the rank of the path (program) found
by ant k. Note that ranking is done with respect to
the L
k
(t, p) of ants. The contribution of ant k to the
update of a trail is computed as follows:
△T
k
(t) = Θ
k
. 2 .
L− n+ 1
L
2
+ L
(3)
The amount of pheromone in T table at time t is up-
date by:
T (t) := (1− p) ∗ T (t − 1)+ △T(t) (4)
Where 0 < p ≤ 1 is the coefficient representing
pheromone evaporation, and
△T (t) =
K
∑
k=1
△T
k
(t) (5)
is the pheromone increase obtained by accumulating
the contributions △T
k
(t) of each ant k = 1,..., K.
EGAP, by using a heuristic function, encourages
ants to first build a good solution structure and then
tune it. The heuristic function is designed to have ants
expand the expression for a fraction of the maximum
number of allowed rules and then select completion
rules for the remainder. Maximum number of using
rules is a constant specified by the user to limit the
total number of rules which an ant can select to gen-
erate its own expression (program). Expression con-
struction has two phases: expanding the expression
and completing the expression. The first phase will
be performed in a fraction of maximum number of us-
ing rules and the second phase will be done in the
remainder.
From this perspective, the rules of a grammar fall
into two categories: expanding rules and completing
rules. Expanding rules tend to expand the expression
by producing some other non-terminal symbol as op-
posed to completing rules which have a tendency to
replace the non-terminal symbols of the expression
with terminal ones. EGAP presents an expanding fac-
tor (f
e
) that shows to what extent a rule is an expand-
ing rule. High values of f
e
demonstrate the high prob-
ability of being an expanding rule while low values
shows the high probability of being completing rule.
Not only can the rules have an expanding factor but
also the non-terminal symbols have expanding factor
related to their rules’ expanding factors.
To calculate f
e
for all the rules and non-terminal
symbols, EGAP uses an iterative algorithm. This al-
gorithm first initializes the expanding factor ( f
e
) of
all the rules and non-terminal variables with a large
value. Then it updates the expanding factor of each
rule during every iteration. Each rule adds together
the expanding factor of the non-terminal symbols that
it generates and finally increments them by 1. Each
non-terminal variable updates its expanding factor by
calculating the average over all of its rules. The up-
date formula is:
f
e
(x,i) = [
∑
y ∈ nt
f
e
(y,0) ] + 1 i = 1...N (6)
f
e
(x,0) = mean f
e
(x,i) i = 1. . . N (7)
Where f
e
(x,i) is the expanding factor of the ith
rule of the non-terminal symbol x and nt is the set of
all non-terminal symbols included in that specific rule
(ith rule). f
e
(x,0) is the expanding factor of the non-
terminal symbol x.
EGAP has used the following heuristic function:
H ( x,i,n) = e
t
n
− n
t
n
∗( log( f
e
(x,i) + 1)
(8)
Where x is a non-terminal symbol and i is an index of
x’s rules. Furthermore, n is the number of rules that an
ant has applied so far to reach its current expression
and t
n
is the constant threshold related to changing
THE UPHILL BATTLE OF ANT PROGRAMMING VS. GENETIC PROGRAMMING
173

the phase of the construction (1 < t
n
< maxN) while
maxN is the maximum number of using rules for ants.
As mentioned previously, ants choose their path based
on the amount of pheromone deposited on the edges,
the formula below gives us the probability of selecting
each edge:
P
k
e
(t) =
[T
e
(t)]
α
.[η
e
]
β
∑
c∈C(n
′
)
[T
c
(t)]
α
.[η
c
]
β
(9)
Where P
k
e
(t) is the probability of selecting the
edge e and T
e
(t) is the amount of pheromone de-
posited on the edge e and η
e
is a heuristic value re-
lated to the selection of the edge e. C(n
′
) is the candi-
date set, the edges which can be selected when the ant
is on the node n
′
. The experimental parameters α and
β control the relative importance of pheromone trail
versus heuristic function.
4 EXPERIMENTAL RESULTS
In this section, the performance of EGAP and GP
will be compared in three experiments: Quartic sym-
bolic regression, Multiplexer, and Santa Fe ant trail.
These experimentsare chosen as EGAP outperformed
GAP in the same set of experiments (Salehi-Abari and
White, 2008).
The evaporation rate, p, is 0.5 and α and β are
set to 2 and 1 respectively. The initial pheromone
concentration, T
0
, is 10
−6
and maxN is 100. We set
the EGAP parameters the same value as suggested in
(Salehi-Abari and White, 2008). For EGAP, 10 sim-
ulations are run with 100 iterations and 20 ants have
passed through the graph in each iteration.
All experiments performed for GP use the
GPLAB environment (Silva and Almeida, 2005).
Populations of 25 individuals (randomly initialized,
maximum depth of 17) were evolved for 80 genera-
tions. All the settings of the GP are set to the default
settings of GPLAB; function and terminal sets and fit-
ness function are defined separately for each experi-
ment. For GP, 10 simulations are run with 80 genera-
tions.
For both of the algorithms (EGAP and GP), the
number of generated individuals is equal, which re-
sults in a fair comparison of the two algorithms. In
GP, 80 generation of 25 individuals (80*25=2000)
while in EGAP 100 iterations for 20 ants (100*20 =
2000). We chose 100 iterations of 20 ants for EGAP
because this number of iterations was used in the orig-
inal paper (Salehi-Abari and White, 2008), and the
best performance was achieved using these settings.
EGAP generally needs more iterations as opposed to
GP which often gives superior performance with a
larger population. We could have chosen 25 ants and
80 iterations (similar to the GP setting); however, this
provided inferior EGAP results. That is why we chose
the parameters such that the total number of evalua-
tions is the same for both techniques (80* 25 = 100 *
20 = 2000).
4.1 Quartic Symbolic Regression
The target function is defined as f(a) = a+ a
2
+ a
3
+
a
4
, and 200 numbers randomly generated in the range
of [-10,10] are used as the input for this function and
the corresponding output of them is found. Therefore,
the desired output for these 200 input numbers will be
these outputs called the y vector. The objective of this
experiment is that these two algorithms (EGAP and
GP) find the expression that has the nearest output to
y for a given x input vector. The fitness function for
all the two algorithms is defined as follows:
f(p,x,y) =
1
N
N
∑
n=1
|p(x(n)) − y(n)| (10)
Fitness(p, x, y) =
1
1+ f(p,x,y)
(11)
Where p is the expression generated by the automatic
programming algorithm; x and y are the input vector
and desired output vector respectively. Finally, N is
the number of the elements of x. The grammar used
in this experiment for EGAP is given by:
< expr > → < expr >< op >< expr > | < var >
< op > → ∗ | − | + | /
< var > → a
And the function set and terminal set for GP are:
Function set = {∗,−,+, /}
Terminal Set = {a}
0
0.2
0.4
0.6
0.8
1
0 20 40 60 80 100
Fitness
Iteration/Generation Number
EGAP
GP
Figure 2: Plot of the mean of the best fitness on quartic
symbolic regression problem over 100 iterations.
In Figure 2, the plot of the mean best fitness over
10 runs can be seen. GP outperforms EGAP in this
experiment. A t-test comparing these two methods
IJCCI 2009 - International Joint Conference on Computational Intelligence
174

gives a score of 1.18 in favor of GP – significant at
the 75% confidence level.
4.2 4-to-1 Multiplexer
The goal of this problem is to find a boolean expres-
sion that behaves as a 4-to-1 Multiplexer. There are
64 fitness cases for the 4-to-1 Multiplexer, represent-
ing all possible input-output pairs. Program fitness
is the percentage of input cases for which the gen-
erated boolean expression returns the correct output.
The grammar adopted for this problem is as follows:
<mexpr> → < mexpr> < op2 >< mexpr>| <
op1 >< mexpr>| < input>
<op1 > → and | or
<op2 > → not
< input >→ in
0
|in
1
|in
2
|in
3
|in
4
|in
5
And the function set and terminal set for GP are:
Function set = {and,or, not}
Terminal Set = {in
0
, in
1
,in
2
,in
3
,in
4
,in
5
}
A plot of the mean best fitness over 10 runs for these
two algorithms is illustrated in Figure 3. As shown,
GP had the better performance compared to EGAP.
GP represents a statistically significant improvement
over EGAP for this problem. A t-test comparing these
two methods gives a score of 9.360 in favor of GP –
significant at the 99.5% confidence level.
0
0.2
0.4
0.6
0.8
1
0 20 40 60 80 100
Fitness
Iteration/Generation Number
EGAP
GP
Figure 3: Plot of the mean of the best fitness on multiplexer
problem over 100 iterations.
4.3 Santa Fe Ant Trail
The Santa Fe ant trail is a standard problem in the
area of GP. The objective of this problem is to find a
computer program to control an artificial ant in such a
way that it finds all 89 pieces of food that are located
on the discrete trail. The ant can only turn left, right,
or move one square ahead. Also, it can check one
square ahead in the direction facing in order to recog-
nize whether there is a food in that square or not. All
actions, except checking the food, take one time step
for the ant to execute. The ant starts its foraging in the
top-left corner of the grid. The grammar used in this
experiment is:
< code > →< line > | < code > < line >
< line > →< condition > | < op >
< condition > → if( food ahead())
{ < line > }
else
{< line >}
< op > → left(); | right(); | move();
And the function set and terminal set for GP is:
Function set = {antI f}
Terminal Set = {antMove, antRight, antLeft}
The fitness function for both algorithms is the
number of food items found by ant over the total num-
ber of food items, which is equal to 89.
0
0.2
0.4
0.6
0.8
1
0 20 40 60 80 100
Fitness
Iteration/Generation Number
EGAP
GP
Figure 4: Plot of the mean of the best fitness on ant trail
problem over 100 iterations.
In Figure 4, the plot of the mean best fitness over
10 runs for the ant trail problem can be seen. GP out-
performs the EGAP in this experiment. A t-test com-
paring these two methods gives a score of 2.847 in
favor of GP – significant at the 99% confidence level.
4.4 Discussion
The main contribution of this paper is the compari-
son of well-known genetic programming to EGAP, a
representative of the ant programming approach. As
shown in the previous experiments, GP outperforms
EGAP on three well-known (Quartic symbolic regres-
sion, multiplexer and Santa Fe ant trail).
An intriguing question is, why does GP outper-
forms EGAP when EGAP provides more complex
control over the evolutionary process? By analyzing
the Figures 2, 3 and 4, we hypothesize that EGAP
suffers from premature convergence. Especially in
multiplexer and ant trail experiments, we observe that
EGAP converges prematurely before reaching itera-
tion 20. As premature convergence can happen in
THE UPHILL BATTLE OF ANT PROGRAMMING VS. GENETIC PROGRAMMING
175

cases of loss of genetic variation when every individ-
ual in the population is identical, we analyzed how
many distinct solutions are being generated by each
method. In this sense, if one method in a specific ex-
periment converges prematurely, it will generate more
identical solutions than the method which does not
converge prematurely on that experiment.
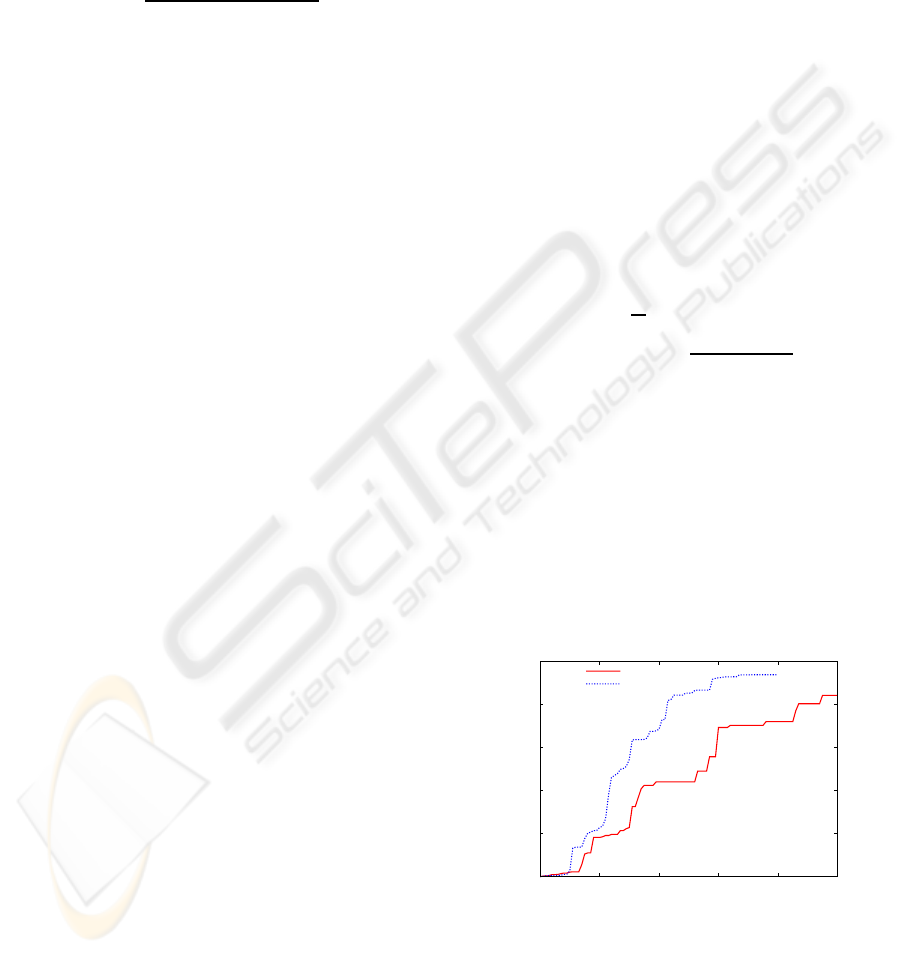
Figure 5: The average of distinct generated solutions.
Figure 5 shows the average of distinct generated
solutions over 10 simulations for each method in
three experiments. EGAP was successful in gener-
ating diversity solutions in Quartic symbolic regres-
sion experiments and that is why the performance
of EGAP in this experiment is comparable to GP’s
performance. In contrast, EGAP could not generate
as many distinct solutions in two other experiments
(multiplexer and ant trail) and as a consequence GP
had statistically significantly better results.
5 CONCLUSIONS
This paper compares the performanceof GP to EGAP,
a representative of the ant programming approach.
EGAP is a technique designed to generate computer
programs by simulating the behavior of ant colonies.
The performance of EGAP with GAP was compared
on 3 well-known problems: Quartic symbolic regres-
sion, multiplexer and Santa Fe ant trail. The re-
sults obtained demonstrate that GP has statistically
superior performance. EGAP despite its complexity
does not offer any advantages over the simple and
traditional genetic programming. In our view, un-
til a mechanism is put in place to reintroduce diver-
sity, EGAP approaches will continue to struggle to be
competitive with GP.
The future work for ant programming approaches,
especially EGAP, includes utilizing a similar diversi-
fication mechanism reported in (Gambardella et al.,
1997). The diversification mechanism is activated if
during the predefined period there is no improvement
to the best generated solution. Diversification consists
of resetting the pheromone trail matrix.
We hypothesize that the power and advantage of
GP over swarm-based automatic programming is in
its exploration ability. We are interested in comparing
current automatic programming approaches in terms
of their exploration abilities in our ongoing research.
REFERENCES
Bonabeau, E., Dorigo, M., and Theraulaz, G. (1999).
Swarm Intelligence: From Natural to Artificial Sys-
tems. Oxford.
Boryczka, M. (2002). Ant colony programming for ap-
proximation problems. In Proceedings of the IIS’2002
Symposium on Intelligent Information Systems, pages
147–156. Physica-Verlag.
Boryczka, M. and Czech, Z. J. (2002). Solving approx-
imation problems by ant colony programming. In
GECCO ’02, page 133, San Francisco, CA, USA.
Morgan Kaufmann Publishers Inc.
Gambardella, L., Taillard, E., and Dorigo, M. (1997). Ant
colonies for the qap. Technical report, 4-97, IDSIA,
Lugano, Switzerland.
Keber, C.and Schuster, M. G. (2002). Option valuation with
generalized ant programming. In GECCO ’02, pages
74–81, San Francisco, CA, USA. Morgan Kaufmann
Publishers Inc.
Koza, J. R. (1992). Genetic programming: on the program-
ming of computers by means of natural selection. MIT
Press, Cambridge, MA, USA.
Koza, J. R. (1994). Genetic programming II: automatic dis-
covery of reusable programs. MIT Press, Cambridge,
MA, USA.
Koza, J. R., Andre, D., Bennett, F. H., and Keane, M. A.
(1999). Genetic Programming III: Darwinian Inven-
tion & Problem Solving. Morgan Kaufmann Publish-
ers Inc., San Francisco, CA, USA.
Miller, J. F. and Thomson, P. (2000). Cartesian genetic pro-
gramming. In Proceedings of the European Confer-
ence on Genetic Programming, pages 121–132, Lon-
don, UK. Springer-Verlag.
O’Neill, M. and Brabazon, A. (2006). Grammatical
swarm: The generation of programs by social pro-
gramming. Natural Computing: an international
journal, 5(4):443–462.
Roux, O. and Fonlupt, C. (2000). Ant programming: Or
how to use ants for automatic programming. In ANTS’
2000, pages 121–129.
Salehi-Abari, A. and White, T. (2008). Enhanced general-
ized ant programming (egap). In GECCO ’08, pages
111–118, New York, NY, USA. ACM.
Silva, S. and Almeida, J. (2005). Gplab-a genetic program-
ming toolbox for matlab. In Proceedings of the Nordic
MATLAB Conference (NMC-2003), pages 273–278.
IJCCI 2009 - International Joint Conference on Computational Intelligence
176