
ASSORTMENT OF SOLUTIONS FOR VARIABLE TASKS IN
MULTI-OBJECTIVE PROBLEMS
Gideon Avigad, Erella Eisenstadt and Uri Ben Hanan
Ort Braude College of Engineering, Karmiel, Israel
Keywords: Multiobjective, Evolution, Engineering design.
Abstract:
I
n the same manner that species are associated with variants in order to survive, and that human
communities, apparently in order to survive, are built up from people with different skills and professions,
we suggest in this paper to select a set of diverse solutions in order to optimally solve Multi-Objective
Problems (MOPs). As a set, the solutions may cover a wider range of capabilities within the multi-objective
space than is possible for an individual member of the set. The diversity within the set is a key issue of this
paper and hereinafter designated as an assortment. In the paper, we suggest a computational tool that
supports the selection of such an assortment. The selection is posed as an auxiliary MOP of cost versus
variability. The cost is directly related to the size of the assortment, whereas the variability is related to the
ability of the assortment to cover the objective space. A previously treated problem is adopted and utilized
in order to explain and demonstrate the approach.
1 INTRODUCTION
The use of Evolutionary Multi-objective
Optimization, (EMO) is a popular approach for
searching for solutions to MOPs (Multi Objective
Problems). Commonly when the objectives of a
MOP are contradicting the solution to the MOP is
the Pareto set. The development of Pareto-based
evolutionary algorithms has been initiated by the
procedure suggested by Goldberg, (1989). Surveys
and descriptions of EMO algorithms can be found in
several references (e.g., Deb, 2001).
Selecting a solution out of a Pareto set is
commonly based on the designers' preferences.
Choosing a set of solutions to MOPs instead of
selecting a single solution is relatively a new area of
research.
Recently a new approach to select conceptual
solutions has been investigated (e.g., Mattson, and
Messac, 2005). It involves Set-Based Concept
(SBC) representation in which a concept is
associated with the performances of multiple
solutions. When dealing with SBCs, each of the
solutions (design alternatives), of the SBC is
assumed to be associated with a point in the
objective space, representing its performances.
Therefore the concept performances can be
evaluated based on a cluster of points in the
objective space, where each of the points of the
cluster is associated with the performances of at
least one of the design alternatives (solutions) of the
SBC. According to that approach, each concept has
its related front. The global front, which is the non
dominated set over all the objective space, is the s-
Pareto (Mattson, and Messac, 2005). An approach
for choosing a concept, (a set) which has
representatives on the s-Pareto, has been suggested
in Mattson and Messac, (2005). There, it has been
assumed that, the more representatives a concept has
on the s-Pareto, the more flexible it is in
corresponding to uncertainties. Avigad and
Moshaiov (2009) have highlighted some pitfalls of
considering just the s-Pareto and suggested an
auxiliary MOP of optimality versus variability to
compare between the concepts, based on their entire
individual Pareto fronts.
Apart from selecting a set, the evolution of sets
has also been considered. For instance, there are
studies that use set domination to search for the best
approximation of the Pareto front (e.g., the
Indicator-based Evolutionary Algorithm, -IBEA of
Zitzler and Künzli, (2004). Such a search is based on
assigning a value to the degree of domination
between sets of competing approximations of the
Pareto set. For example, such an assignment is
performed using the binary additive indictor, which
269
Avigad G., Eisenstadt E. and Ben Hanan U. (2009).
ASSORTMENT OF SOLUTIONS FOR VARIABLE TASKS IN MULTI-OBJECTIVE PROBLEMS.
In Proceedings of the International Joint Conference on Computational Intelligence, pages 269-276
DOI: 10.5220/0002277902690276
Copyright
c
SciTePress

was introduced by Zitzler et al. (2003). The binary
additive-indicator of two Pareto set approximations
is equal to the minimum distance among the
dimensions of the objective space by which one
Pareto set approximation needs to move or can be
moved such that the compared approximation is
weakly dominated by it.
Within the context of this paper, it is important to
consider another assessment measure that allows a
comparison between two sets. This measure is the
hyper-volume measure or S metric, which has been
proposed by Zitzler and Thiele, (1998), who called it
the 'size of the space covered' or the 'size of
dominated space.' Van Veldhuizen and Lamont
(2000), described it as the Lévesque measure of the
union of hyper-cubes defined by a non-dominated
point and a reference point. When engineering
design is considered, the reference point might be
related to specified boundaries in the objective
space, namely within a 'region-of-interest'.
According to Mattson and Messac (2005), in order
to define a region-of-interest, the designer should
specify a single point in the objective space.
It is noted that choosing a set might also be
related to the notion of community of robots. In that
case, the aim is to find a set of robots which are
communicating in order to perform a task or tasks.
The idea might be related to swarms (see
http://www.swarm-robotics.org) or to a multi-agent
design (e.g., Bensaid, and Matheieu, 1998).
In contrast to previous studies, which utilize a set
of robots in order to execute an aggregated mission,
the current paper suggests choosing a set such that
its members do not always participate in the mission,
but are rather "called for" based on the mission at
hand. To elucidate the problem that will be attended
by the current paper, refer to the following
illustrative example: Suppose that robotic platforms
are operating in a multi-task environment. This
means that sometimes a fast action is needed and a
robot should quickly move from one place to the
other. In another scenario heavy loads should be
transferred by a robot from one place to the other. It
is clear that if optimality is considered, ideally the
two different tasks should be performed by different
robots. Choosing the optimal variety of robots
(solutions) is the scope of the current paper.
The paper is organized as follows. The next
section lays out the background on which we rely in
order to introduce the suggested approach. Section 3
describes the motivation for this paper, having its
origins in biology, sociology, and engineering
design. Section 4 is the methodology, where the
problem, its solutions, and the search approach are
explained and formulated. In Section 5, an example
is utilized in order to demonstrate the applicability
of the approach in choosing an optimal assortment.
2 BACKGROUND
Recently in Avigad et al. (2009), we have introduced
a new problem within the context of MOPs. The
problem treated in Avigad et al. (2009), although
defined as a common uncertain MOP, differs
inherently from that problem. This difference
influences both the search procedure as well as the
multi criteria decision making. In the following, a
brief outline of the problem and its solution as given
in Avigad et al. (2009) are described. Consider the
following MOP:
)d,x(FMinimize
)x(
(1)
where
T
K21
)]d,x(f),.....d,x(f),d,x(f[)d,x(F =
;
2
K
≥
n
Rx ⊆Ω∈
,
T
n21
]x,.....x,x[x =
m
R,d ⊆Γ∈
,
T
m21
]d,.....d,d[d =
)U()L()U()L(
jjjiii
ddd and xxx ≤≤≤≤
where
Ω
is the design parameters space
(parameters that are to be chosen) and
Γ is the
model's environmental parameters space (which are
not chosen but might be uncertain). x is a solution
T
ni
1
]x,...x,..x[x =
,
n
Rx ⊂Ω∈
where
xxx
)U()L(
iii
≤≤
and
n
R
is the design space
(controlled parameter space). The interval given for
x is commonly related to an uncertainty, which is
related to the realization of an exact value of x.
Factors such as machine precision are the basis for
the interval, which is in fact a tolerance given for
each design parameter. In Avigad et al. (2009), the
origin of the interval is fundamentally different. The
interval is a span of possible values associated with
choosing a specific parameter. For example
choosing a specific motor (with no uncertainty) is
like choosing a span of output torques (as well as
weight, size, etc.). Each of the possible values for all
design parameters is performing within an
environmental situation
m
Rd ⊆Γ∈
T
mj1
]d....d,...d[d =
such that
)U()L(
jjj
ddd ≤≤
and
m
R
are the environmental space (uncontrolled
parameter space). If
Γ×
Ω
⊆
x
S
then
x
x
Ss ∈ is a
IJCCI 2009 - International Joint Conference on Computational Intelligence
270

scenario of x (which is a vector in
mn
R
×
) . A
scenario's vector of performances in a K objective
space is
)s(Fy
x
s
x
=
where
Tx
K
x
2
x
1
x
)]s(F....),s(F),s(F[)s(F =
The corresponding set of all the scenarios'
performances of the solution x is designated as: Y
x
,
K
x
RY ⊆Τ⊆
. This means that a solution is
represented by a cluster of points (each representing
a vector) in objective space. The cluster of possible
scenarios in the work of Avigad et al. (2009), is built
of scenarios that are related to the same solution
whereas in the uncertainty MOP case, each scenario
is a different realized solution. So if all are possible
scenarios, then a comparison between the solutions
should be based on the best. In a multi objective
space, the best might be a set of best scenarios. The
set of best scenarios of a solution x, RS
x
and related
front RSF
x
has been defined in Avigad et al. (2009)
as follows:
}RSs:)s(Fy|y{:RSF
)}s(F)s(F:Ss|Ss{:RS
xxx
ss
x
x'x
x
'x
x
xx
xx
∈=Γ∈=
∈∃¬∈= ≺
(2)
The set of optimal solutions P* and their
representation in objective space, the Pareto Layer,
PL, are defined as follows:
*}Px|RSF)s(F{:PL
}RSRS:RS|x{:*P
xx
x'x'x
∈∈=
∃¬Ω⊆= ≺
(3)
The PL is associated with sets of representative sets,
each related to a solution. This front is not a clear-
cut front but rather a cloud of scenarios'
performances and therefore, it has been termed in
Avigad et al. (2009) as the Pareto layer (PL). Such a
PL possesses solution scenarios' performances that
are dominated by the performances of other
solutions’ scenario's performances. Nevertheless,
the representative sets of the optimal solutions do
not dominate each other.
In Avigad et al. (2009), an MOEA (Multi Objective
Optimization Algorithm), which applies a search for
finding the PL, has been suggested and investigated.
The current paper deals with selecting sub-sets of
the Pareto layer set, based on the motivation
explained in the following section.
3 MOTIVATION
This paper approach is motivated by the apparent
diversity within species in nature and by the
diversity of professions and expertise within human
societies. The genetic diversity carried in natural
populations is a key factor in evolution (e.g., Mayr
1982) and is one of the fundamentals of what is
termed as
modern evolutionary synthesis. The
importance of population diversity is highlighted in
many nature related studies (e.g., Booy, G. et al
2000). According to Booy, G. et al 2000, "Such
genetic variation within a population may allow
species to change over time and thereby survive
changing environmental conditions." According to
Boer et al. 1993, "… a population can only achieve
its adaptability by distribution of the variation across
its individuals". The above citation clearly implies
the importance of variability within a species. The
above biologically related differences are associated
with diversity in the genotype. A question that
needs to be investigated involves phenotypic
differences. Naturally, the dissimilarity of human
faces is one example. However, here we are more
interested in the behavior aspects. A clear
dissimilarity between individuals within a human
community is the existence of different trades, such
that different people within the community are
experts in different fields of knowledge (e.g., a
medic, a coal miner and a fisherman are trades
commonly practiced by different people).
When optimality is considered, this is somewhat
comparable to the fact that there is no world heavy
weight champion winning a 100m run against Usain
Bolt (the current world champion). These two
extremes (strong and fast) are not the only cases. A
decathlon athlete should possess characteristics that
will allow him competing both in speed and
strength. Neither the decathlon athlete, the runner,
nor the heavy lifter athletes, is superior to each other
if the bi-objective space of speed versus strength is
considered. This issue is the base for choosing the
members of an Olympic team. Instead of choosing
one solution (a single superstar that performs
reasonably in all Olympic professions), a set of
solutions (several athletes, each expert at his own
field of profession) are selected. Thus a multi-
objective problem of optimizing all objectives (i.e.,
running the fastest, lifting the heaviest, etc.) is
solved through using a set of solutions (athletes).
Motivated by the apparent importance of
diversity in species and human communities, we
suggest searching for a set of diversified engineering
solutions such that they may optimally comply with
their set related tasks.
Before going on to present the methodology, we
would like to note the following two remarks.
ASSORTMENT OF SOLUTIONS FOR VARIABLE TASKS IN MULTI-OBJECTIVE PROBLEMS
271

1. Choosing a name for the set of solutions within
the context of this paper was not an easy task.
Community, group, team, unit, and other names
were considered. The main drawback of all of these
notions is the inherent interaction between their
members. The definition for an assortment seems to
best fit the idea. According to
en.wiktionary.org/wiki/assortment an assortment is
"a collection of varying but related items
."
No interaction is reminded in that definition, which
is fine, with the relation possibly being interpreted
here as the relation to the same objective space.
2. The current paper is bound to the ideas
presented in Avigad et al. (2000). Here a solution
may have a span of possible performance vectors
rather than a single performance vector. Consider a
100 meters runner that runs slower than his/her best,
or would run slower if s/he carries a load (or if s/he
runs uphill). This is comparable to a design of a cart
to move as fast as possible and to carry the highest
loads. Carrying heavier loads means moving slower
and vice versa. We could think of choosing a set of
cars that could carry as high as possible loads and
move as fast as possible or on a set of telescopic
arms that should carry high as possible loads to most
distant horizontal locations. In these cases there is a
fundamental contradiction in the objective space.
However, more importantly, each solution has a
span of possible performances. This is why the
methodology and the example are built upon the
Pareto Layer notion.
4 METHODOLOGY
4.1 An Assortment of Solutions
An assortment A
s
is a sub-set of all possible
solutions
Ω⊆
s
A ,
∪
s
n
1i
i
s
xA
=
=
where n
s
=
s
A .
Notes:
1. An assortment might possess a single
member.
2. A solution might be a member of more than
one assortment.
3. An assortment might possess identical
members.
The performance of an assortment, Y
s
is represented
in the problem objective space by the union of the
representative sets of the assortment's members,
∪
s
n
1i
i
s
RSFY
=
= where
i
RSF is the representative-set
related front (see Section 2) of the i-th member of
the assortment.
In the current paper we shall follow some
assumptions, which are given and explained here.
1: Following the motivation for optimality, we
only consider solutions that belong to the Pareto set
as candidates for members in an assortment.
2: The boundaries of the performances within the
objective (task) space are known beforehand. In
other words, the task WOI is given
a priori to the
design process. For example, it is assumed that the
maximal carried load is known.
3: The maximal cost involved with the assortment
is known. This might be based on costs of
manufacturing and transportation, among others.
Based on the above assumptions, the assortment
set and related performances are:
*
s
PA ⊆ and PLY
s
⊆
In the current paper, we assume that the Pareto set
and related Pareto Layer are given.
4.2 The Competency of an Assortment
It is suggested here that comparing and selecting an
assortment out of all possible assortments is carried
out by considering their performances. The
performances of an assortment is termed here as the
competency of the assortment. There might be
several measures used to assess this competency. In
the current paper, we consider just two: The first is a
straight forward one, the cost of the assortment. As
the number of members within an assortment
increase, so does its cost. The cost of an assortment
is the sum of the individual members' costs:
∑
=
=
s
n
1i
i
ss
)x(Cost)A(Cost (4)
The second measure is the variability of the
assortment, V
ss
. It is a measure of the capability of
the assortment to cover the objective space. The
issue of variability has been extensively treated in
Avigad and Moshaiov, (2009). Here it is the hyper-
volume rendered by the community related scenarios
as formulized for an assortment A
s
as follows: Let
A
F be the union of all representative sets of an
assortment such that:
∪
s
n
1i
i
A
RSF
=
= . Thus the
variability measure may be defined as:
∏
=
−
=
−
=
K
1k
k
WOI
s
j
s
i
1i
1j
s
i
F
i
ss
y
))HV)(HV(HV(
V
xxs
A
∩∪
(5)
IJCCI 2009 - International Joint Conference on Computational Intelligence
272
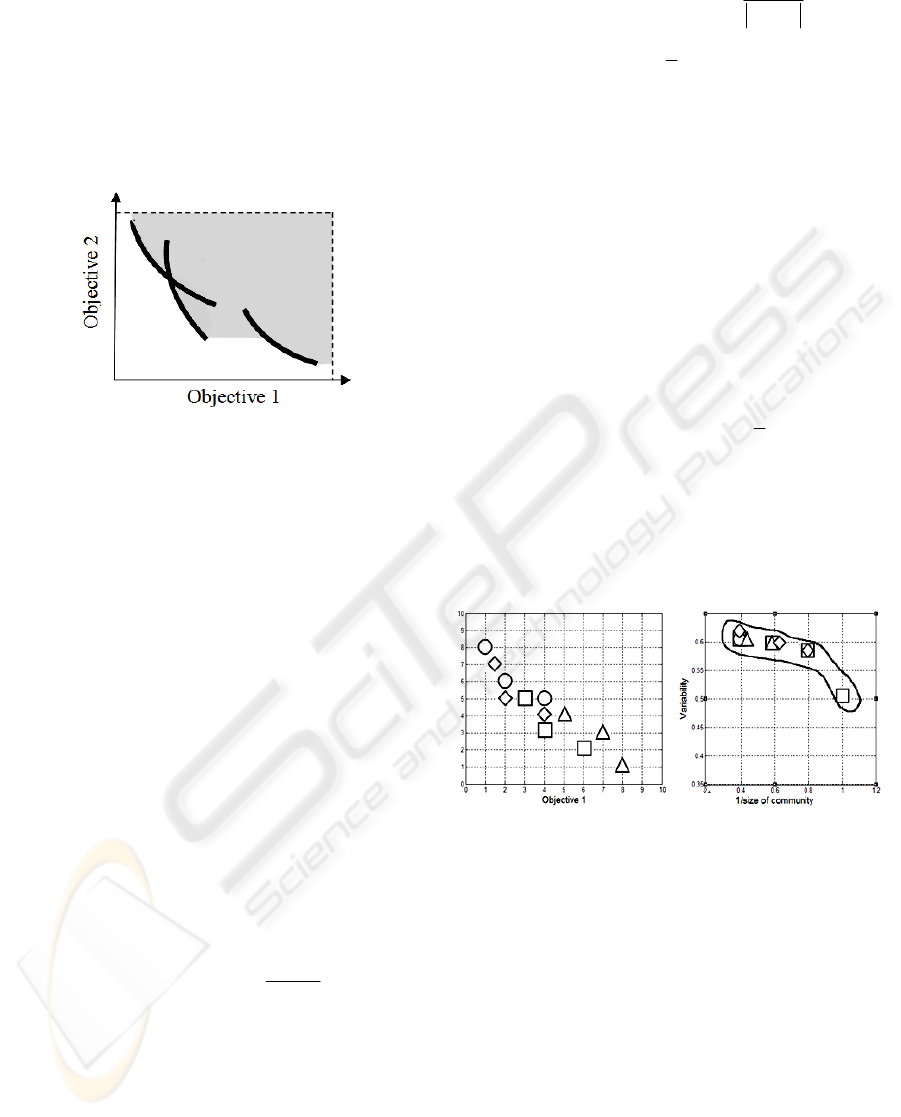
where
x
s
i
HV is the hyper-volume measure of the i-th
scenario belonging to the set F
A
. To elucidate the
measure, refer to Figure 1. The figure depicts the
representative sets of three solutions within a WOI
(designated by dashed lines). The size of the grey
area in the figure is the variability measure. As it
grows, the assortment may comply with more tasks
within the WOI.
Figure 1: Assortment related variability.
The two measures explained above are mapping an
assortment, which is represented by its related
representative sets' fronts in the problem objective
space, into an auxiliary space, which represents the
competency of the assortment. The competency of
an assortment is a point in the auxiliary space
representing the cost associated with the assortment
and its variability. Therefore, the problem of
comparing and selecting between communities is
transformed from the original objective space where
each assortment is represented by a sub-Pareto layer
into the auxiliary objective space where each
assortment is represented by a single competency
point of variability and cost.
4.3 Problem Definition
The problem of finding a sub-set of a Pareto set (an
assortment) is defined as follows:
Find
Ω⊆
s
A , In order to
))A((max
s
A
s
Ψ ,
)
Cost
1
,V()A(
ss
sss
=Ψ
(6)
Following assumption 1 in Section 4.1, the problem
of Equation 6 may be restated as a search for a sub-
set of the Pareto set:
Find
*
s
PA ⊆ , (7)
In order to
)
Cost
1
,V(max
ss
ss
A
s
s.t:
)s(Fy|RSsAx
x
WOIx
x
s
≺∈∃∈∀
Observing Figure 1, it may be understood that as
the size of the assortment grows, its variability also
grows. This means that the MOP that is defined in
Equation 7 involves contradicting objectives.
Therefore the solution, (which is defined in Section
4.4) may involve a Pareto front within the auxiliary
MOP of variability versus cost.
4.4 Problem Solution
The solution to the problem, which has been defined
by Equation 7, is an assortment A
s
* and related
competency Pareto front in the auxiliary MOP, FC*:
*}AA:)A(Z|ZZ{:FC
)}A()'A(:'A|*PA{:*A
sss
***
sssss
≡Ψ=∈=
ΨΨ∃¬⊆= ≺
(8)
To elucidate the notions of Equation 8, refer to
Figure 2. In order to simplify the example, suppose
that the cost is the number of members in an
assortment.
Figure 2: The PL and the optimal assortments.
4.5 Auxiliary MOP's Boundary
Solutions
The boundary solutions of the problem of Equation
8 are; a single solution with the maximal hyper
volume on one side and a set of all the solutions,
which have the scenario/s' performances on global
Pareto front on the other side. This might be seen by
inspecting Figure 3, in which a PL in a bi-objective
space is depicted.
ASSORTMENT OF SOLUTIONS FOR VARIABLE TASKS IN MULTI-OBJECTIVE PROBLEMS
273
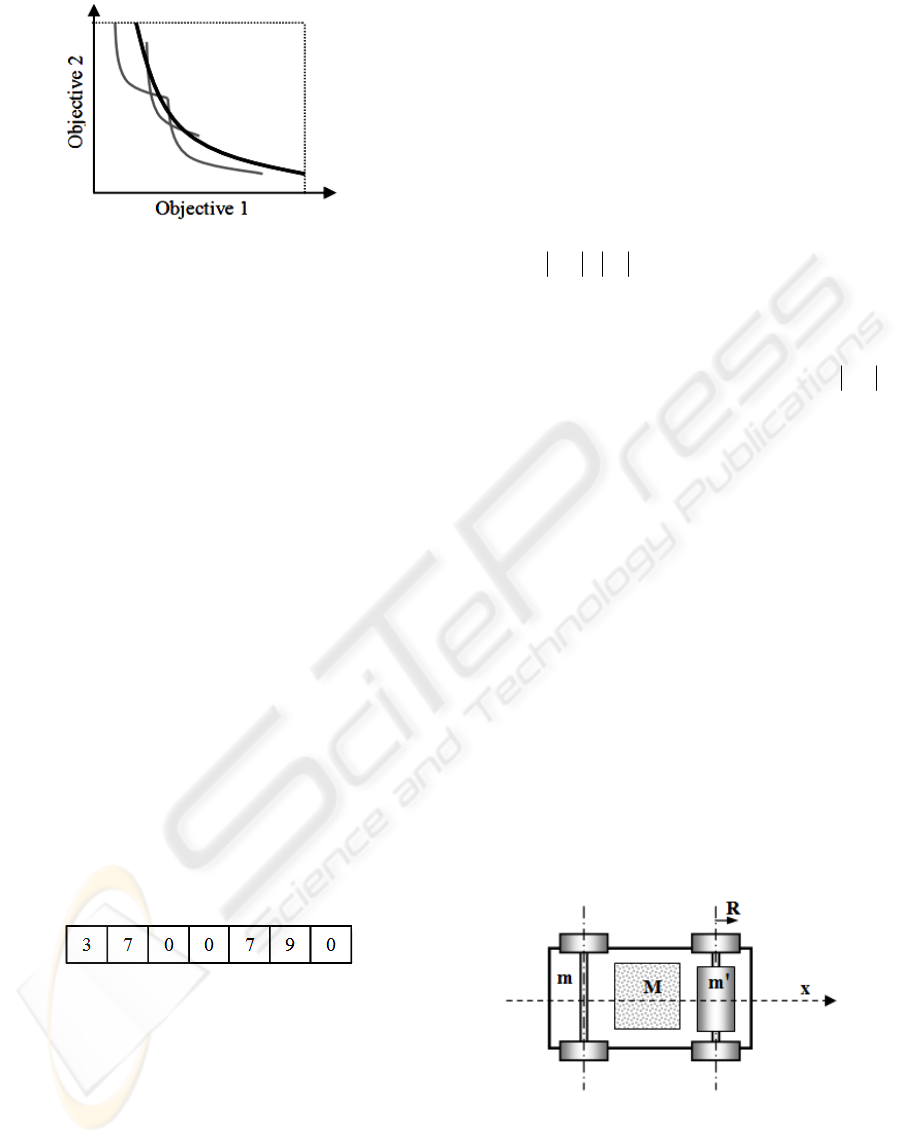
Figure 3: Four PL's solutions RSFs.
The PL is associated with four RSF's of the
solutions. It can be seen that the black related RSF
possesses the highest variability (biggest hyper
volume) when just one member for the assortment is
sorted. Nevertheless, the highest possible variability
would be if all three grey RSFs are combined,
unfortunately at the expanse of cost (three
members). The question is how to find the solutions
which are not the boundary solutions. Here we
suggest using EMO for that search.
4.6 The Evolutionary Search
In this paper, it is assumed that the Pareto set and the
related PL, are given. Therefore, in the current
paper, the focus is on the search for sub-sets of the
optimal solutions' set in order to comply with
Equation 8. The evolutionary search involves a
single chromosome integer value code for each
individual. The length of the individual is predefined
and is usually constrained by transportation volume
or maximal cost boundary. Decoding an individual
results in both the size of the assortment as well as
which of the solutions (found by using the procedure
of (Avigad et al., 2009)) are to be used for the
assortment. For example, depict the coded individual
of Figure 4.
Figure 4: An Individual.
Decoding the individual of Figure 4, results in a four
member assortment with solutions 3, 7 (twice) and 9
as its members. Any MOEA may be used for the
evolutionary search. Here we have used the NSGA-
II (Deb et al. 2002), which is given in the following
with some added details that relate the algorithm to
the current methodology:
Store the RSFs of all P* solutions (see equations…
and (
Avigad et al. 2000) for details how to evolve
them).
1. Initialize a population
t
P
with n individuals.
create Q
t
=
t
P
2. Create a combined population
ttt
QPR ∪=
.
3. Decode R
t
and compute the competency of all
assortments using equations 4 and 5.
4. Perform a non-dominated sorting for
*Z and
find fronts,
i
Fr
, i=1,…,n
r
where n
r
is the
number of fronts in a generation.
5. Initialize a new parent population
∅
=
+1t
P . Set
a non-dominance level counter i=1.
While
nFrP
i1t
≤+
+
, include the i-th front in
the new parent population:
i1t1t
FrPP +=
++
and
set i=i+1.
6. Perform the Crowding Sort procedure (see
(Deb et al., 2002)), and complete the filling of
1t
P
+
with the most widely spread
1t
Pn
+
−
solutions using the Crowding Distance measure
of (Deb et al., 2002).
7. Create offspring population
*
1t
Q
+
from
1t
P
+
by
Tournament Selection.
8. Perform crossover to obtain
**
1t
Q
+
from
*
1t
Q
+
.
9. Perform mutation to obtain
1t
Q
+
from
**
1t
Q
+
.
10. If last generation Go to 12
11. Go to 2
12. Introduce the FC* (Equation 8) to decision
makers.
5 EXAMPLE
The example described in this section proceeds from
Avigad et al. (2000). A cart of mass m(m') driven by
a motor and gear with a mass of m' is to be designed.
m(m'), meaning that as the chosen motor gets
heavier, the carrying cart should be bigger and
heavier in order to support the motor. The cart is
carrying a load M as depicted in Figure 5.
Figure 5: The cart.
Considering a movement of the cart along the x axis,
and that the overall mass is m*=m(m')+m'+M, the
following relaxed equation has been shortly
developed in (Avigad et al., 2009)
IJCCI 2009 - International Joint Conference on Computational Intelligence
274
0gm)x(f
R
)'m(T
*
r
=−
, (9)
where T, is the driving moment beyond the
transmission gear, which depends on the motor
size/mass (i.e., the bigger the stronger) and may
change such that:
max
TT0
≤
≤ . R=0.05m is the
wheel diameter, and f
r
is the rolling resistance force
that may be computed for inflation wheel-pressure
of 30 psi,
5.2
r
)x(002.001.0f
+=
. Let
m(m')=mo+2*m' where mo=4kg. The following bi-
objective problem, which maximizes the speed and
carried load of the cart, i.e.,
)M,xmax(
has been
considered. T and m' are motor dependent and are
taken from Pittman
TM
motor data. The resulting PL
is depicted in Figure 6, which is borrowed from
Avigad et al. (2000).
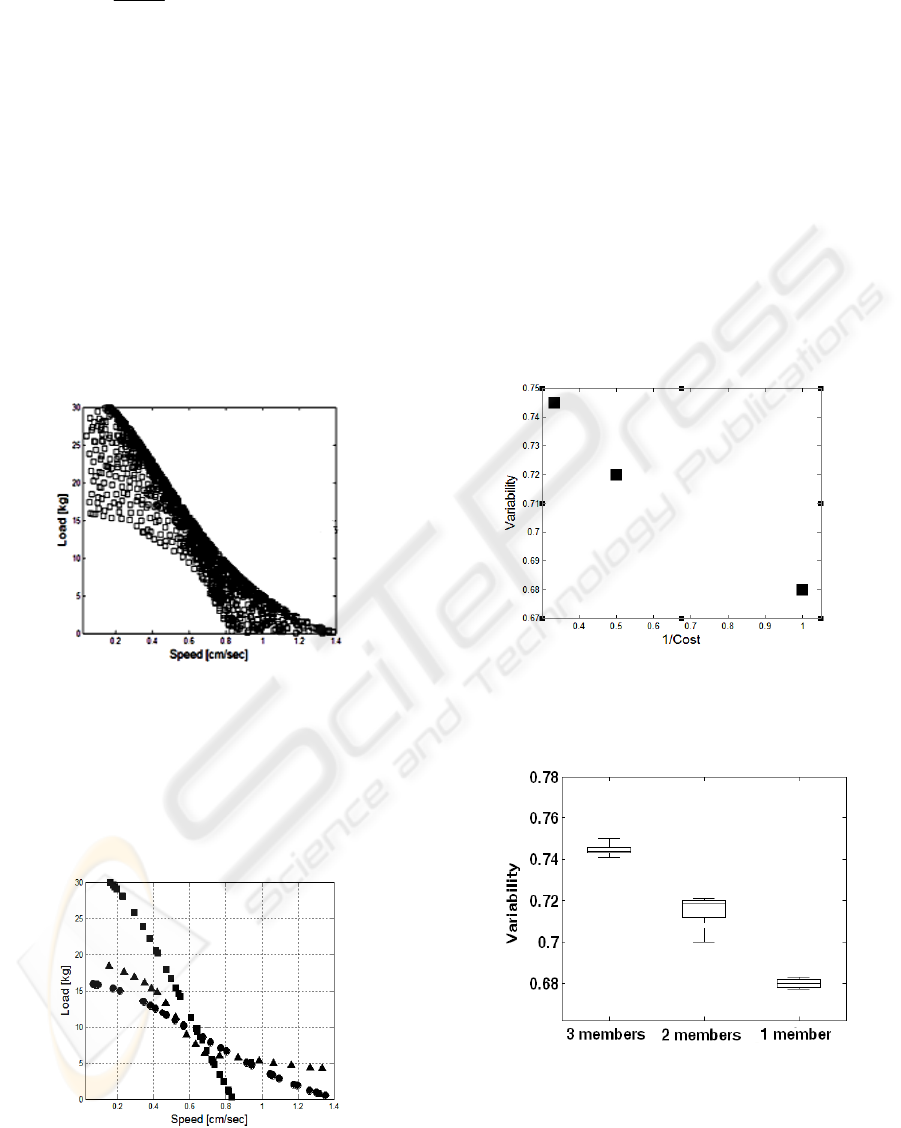
Figure 6: The Pareto Layer of the problem.
The algorithm, which was given in Section 4.6, has
been utilized in order to search for the optimal
assortments. A population of 100 individuals with
50%, 3% crossover and mutation rates respectively
were used. The Pareto front of the auxiliary MOP is
found and is depicted in Figure 7.
Figure 7: The most variable yet expensive assortment.
It is observed that there are three possible different
assortments consisting of one, two or three
members. The solution to equation 8 is depicted in
Figure 8. In the figure, each square represents an
optimal assortment. The leftmost square represents
the three member assortment (all solutions of Figure
7). Although its cost is high compared to other
assortments, its variability is the largest. This means
that if all there carts are available more performance
demands may be complied with. The middle square
represents the two cart assortment with its medium
competency. The rightmost square represents the
single cart assortment, which has the least variability
but with the least cost. Choosing one of the
assortments is up to the DMs, who should consider
their available resources, versus the gain of
variability.
Figure 8: The auxiliary problem Pareto front.
The algorithm was run 50 times for the current
problem. The statistical data is depicted in Figure 9.
Figure 9: Statistical results for the cart problem.
The Figure depicts the spread of the resulting
variability for the three assortments as related to
their variability.
ASSORTMENT OF SOLUTIONS FOR VARIABLE TASKS IN MULTI-OBJECTIVE PROBLEMS
275

6 CONCLUSIONS
In the paper, we introduce the notion of an
assortment, suggest an auxiliary MOP whose
solution may aid decision makers in choosing an
optimal assortment. Furthermore, an EMO to solve
the auxiliary MOP is suggested. The paper
contributions are: a. A new kind of a set (the
assortment) is represented and motivated, b. A need
to choose a set based on a set of sets has been
encountered here for the first time by using EC, c.
New motivation to correlate nature and sociology to
engineering design has been suggested d. A new
motivation for variability within engineering design
has been highlighted, e. Yet another use of MOEA's
has been explored.
Future work should consider searching for
assortments based on the auxiliary MOP directly
from the beginning without relying on an
a priori
search of the PL. Furthermore, some more examples
and test cases should be explored. Among the
investigated cases, problems with more objectives,
both in the original and the auxiliary MOPs should
be interesting. Finally, robustness, while choosing an
assortment, should be an important issue. Gaining
more robustness may call for a need for overlapping
of RSFs, which may reduce variability.
REFERENCES
Avigad G., Eisenstadt, E., and Goldvard A., Report no
Br.11709, at http://mech.braude.ac.il/gideonavigad/
Avigad, G., Moshaiov, A., Set-based Concept Selection in
Multi-objective Problems: Optimality versus
Variability Approach, Journal of Engineering Design,
Vol. 20(3) pp: 217 – 242, 2009
Bensaid, N. and Matheieu, P. An Autonomous Agent
System to Simulatea Set of Robots Exploring a
Labyrinth, In the proceedings of 11th International
FLAIRS Conference, pp: 384-388, Sanibel, Florida
May, 17-20, 1998.
Boer, P., Szyszko, K., and Vermeulen, R. Spreading the
risk of extinction by genetic diversity in populations of
the carabid beetle, Netherlands Journal of Zoology, 43,
242-259, 1993.
Booy, G. et al., Genetic Diversity and the Survival of
Populations. J. Planet Biology 2, 379-395, 2000.
Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. A
Fast and elitist multiobjective genetic algorithm:
NSGA–II, IEEE Transactions on Evolutionary
Computation, 6(2):182–197, April 2002.
Deb K., Multi-objective optimization using evolutionary
algorithms. J. Wiley & Sons, Ltd, 2001.
Goldberg, D.E., Genetic algorithms in search,
optimization and machine learning, Addison-Wesley,
1989.
Marler, R.T., and Arora, J.S. Survey of multi-objective
optimization methods for engineering, Structural
Multidisciplinary Optimization, 26: 369–395, 2004.
Mattson, C. A., and Messac, A. Pareto frontier Based
concept selection under uncertainty, with
visualization, Optimization and Engineering, 6: 85–
115, 2005.
Mayr E. 1982. The growth of biological thought: diversity,
evolution and inheritance. Harvard, Cambs. p567 et
seq.
Pareto, V. 1906: Manuale di Economica Politica, Societa
Editrice Libraria. Milan; translated into English by
A.S. Schwier as Manual of Political Economy, edited
by A.S. Schwier and A.N. Page, 1971. New York:
A.M. Kelley
Van Veldhuizen, D.A., and Lamont, G.B. Multiobjective
evolutionary algorithms: analyzing the State-of-the-
Art, Evolutionary Computation, 8(2): 125-147, 2000.
Zitzler, E., Thiele, L.: Multiobjective Optimization Using
Evolutionary Algorithms—A Comparative Study. In
Eiben, A.E., ed.: Parallel Problem Solving from
Nature V, Amsterdam, Springer-Verlag 292–301,
1998.
Zitzler, E., L. Thiele, M. Laumanns, C. M. Fonseca, and
V. G. da Fonseca (2003). Performance assessment of
multiobjective optimizers: An analysis and review.
IEEE Transactions on Evolutionary Computation 7(2),
117–132, 2003.
Zitzler, E., and K¨unzli, S. Indicator-Based Selection in
Multiobjective Search, Proceedings of the 8th
International Conference on Parallel Problem Solving
from Nature (PPSN VIII) September 2004,
Birmingham, UK
IJCCI 2009 - International Joint Conference on Computational Intelligence
276
