TRAINING FOURIER SERIES NEURAL NETWORKS TO MAP
CLOSED CURVES
Krzysztof Halawa
Department of Electronic, Wrocław University of Technology, Wyb. Wyspiańskiego 27, Wrocław, Poland
Keywords: Orthogonal neural networks, Closed curves.
Abstract: The paper presents the closed curve mapping method using several Fourier series neural networks having
one input and one output only. The proposed method is also excellently fitted for a lossy compression of
closed curves. The method does not require a large number of operations and may be used for multi-
dimensional curves. Fourier series neural networks are especially well fitted for described purposes.
1 INTRODUCTION
Fourier Series Neural Networks (FSNNs) belong to
the class of orthogonal neural networks which have
been outlined, among other publications, in (Zhu,
2002), (Sher, 2001), (Tseng, 2004), (Rafajlowicz,
1994), (Halawa, 2008). These are feedforward
networks. The output value of SISO FSNNs (Single-
Inputs Single-Output FSNNs) is given by the
following formula
,)sin()cos()(
ˆ
10
∑∑
=
+
=
+=
M
m
mmN
N
n
nn
ubwuawuf
(1)
where u is the network input, N and M are
sufficiently large numbers, w
1
,w
2
,…,w
N+M
are the
network weights, which values subject to changes
during training process, a
0
,a
1
,…,a
N
, b
1
,b
2
,…,b
M
are
some natural numbers which meet the conditions
a
0
≠a
1
≠…≠a
N
and b
1
≠b
2
≠…≠b
M
. If N=M and
a
0
=0,a
1
=1,…,a
N
=N and also b
1
=1,b
2
=2,…,b
N
=N,
then (1) is the Fourier series.
FSNNs have numerous essential advantages of
which the following are worth mentioning:
• the output is in linear relation to the weights,
• large speed of training caused by the lack of
local minima of some popular cost functions
(such situation is present, for instance, for the
sum of error squares),
• the relationship between the number of neurons
and the number of inputs and outputs is known,
• values of weights may be easily interpreted,
• there are no problems with arrangement of
centres which exist in networks with radial
basic functions (RBFs).
The functions cos(a
1
u),...,cos(a
N
u) and
sin(b
1
u),...,sin(b
M
u) are orthogonal on the interval
[0,2π) and [-π,π). The scale of u shall be selected so
as the value of SISO FSNN input falls within one of
these intervals.
FSNN have the property of periodicity, i.e.
),2(
ˆ
)(
ˆ
πγ += ufuf
(2)
where γ is integer. Because of this property, FSNNs
are especially well fitted for mapping closed curves.
Further in the text, the closed curve mapping
method is illustrated for several SISO FSNNs. The
outcomes presented refer to networks of various
sizes. In Section 3, there is the procedure to be used
when images has not all black pixels belonging to
the closed curve. Section 4 is dedicated to the
procedure applicable to disturbed images. Section 5
includes short comparison with some other methods
for closed curves mapping.
2 METHOD OF TRAINING
FSNNS TO MAP CLOSED
CURVES
Figure 1 illustrates an example of monochromatic
free-of-distortion image, resolution of 174x94
pixels, with a two-dimensional closed curve of a
tank-like shape.
526
Halawa K. (2009).
TRAINING FOURIER SERIES NEURAL NETWORKS TO MAP CLOSED CURVES.
In Proceedings of the International Joint Conference on Computational Intelligence, pages 526-529
DOI: 10.5220/0002280205260529
Copyright
c
 SciTePress

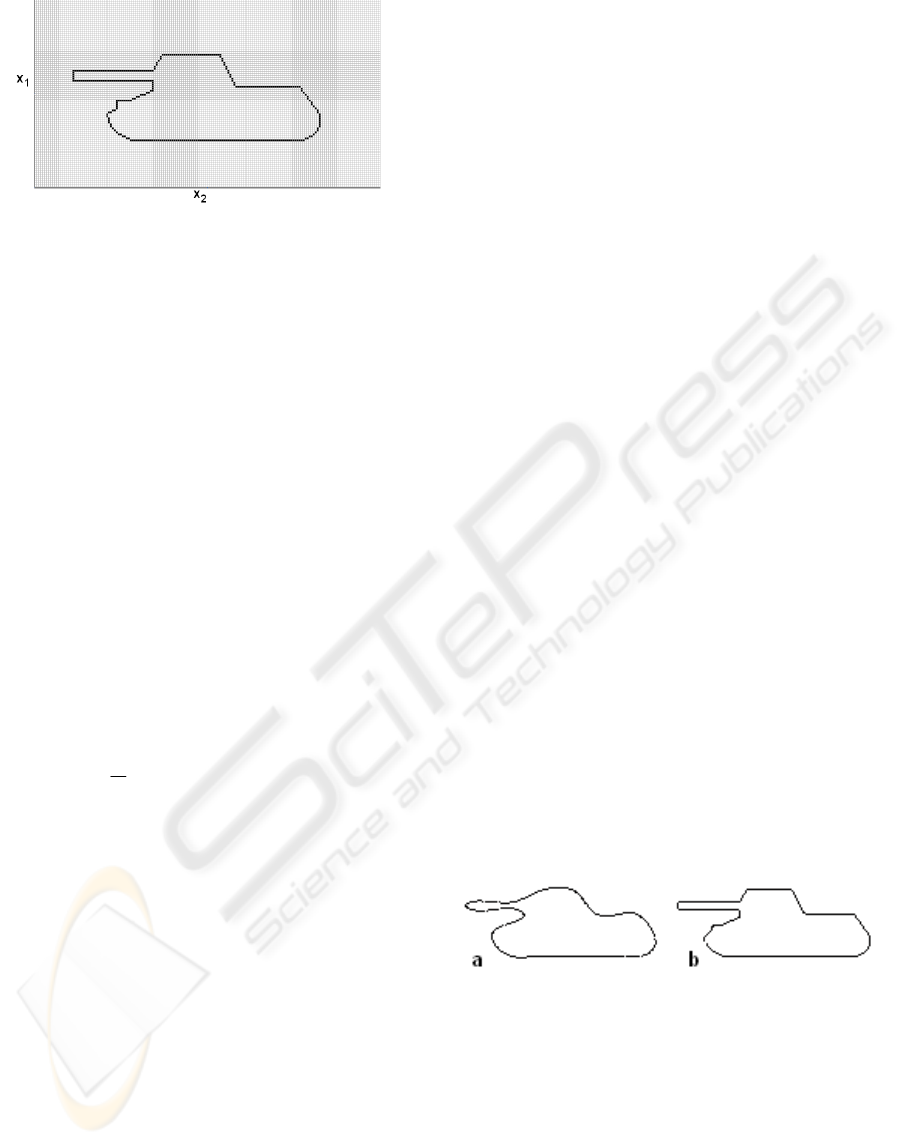
Figure 1: The closed curve of a tank-like shape.
We are denoting the number of black pixels in
Figure 1 as P. Let’s assume an arbitrary black pixel
as the starting point (in the paper, the extreme left-
hand upper end of the barrel was used). Moving
along the closed curve in selected direction, let’s
number all successive black pixels from 0 to P-1. It
is recommended to make the numbering in such a
way that the neighbouring pixels have assigned
numbers differing by no more than 2.
Let x
1
(k) and x
2
(k) denote the coordinates x
1
and
x
2
of k-th pixel, respectively, where k=1,2,...,P-1.
Let’s create two SISO FSNNs. One of them shall be
trained using the training set composed of the pairs
,)}(,{
1
0
1
−
=
P
k
k
kxu
where x
1
(k) is the desired output
value, when the network input equals to u
k
=2πk/P.
The other network is trained using the training set
.)}(,{
1
0
2
−
=
P
k
k
kxu
We can notice that the condition
0≤u
k
<2π is met. As the cost function, we may select,
for example, the mean square function
()
,)()(
ˆ
1
2
1
0
∑
−
=
−=
P
k
kk
uruf
P
J
(3)
where r(u
k
) is the desired output value of the trained
network (for the first FSNN, r(u
k
)=x
1
(k), while for
the second one, r(u
k
)=x
2
(k) ). If the minimization is
made for the function (3), the least squares method
is the most convenient to determine the values of
weights (
Groß, 2003). Upon completing the training
process for the network, the closed curve may be
approximated by plotting the pixels with the
coordinates
(
)
)(
ˆ
),(
ˆ
21 krkr
ufuf
,where
)(
ˆ
),(
ˆ
21 krkr
ufuf
denotes output values, rounded to the closest integer
values, of the first and the second networks, when
their inputs are equal to u
k
. Since the points plotted
in this way need not contact each other, it is
additionally recommended to run interpolation of the
curve under consideration by interconnecting with
straight line the pixels of the coordinates
(
)
)(
ˆ
),(
ˆ
21 krkr
ufuf
and
()
ˆˆ
(),()
1121
fu f u
rk r k++
, which
are not neighbouring each other.
The method presented may be also used, in an
analogous way, for d-dimensional closed curves,
where d is natural number greater than or equal to 2.
The proposed algorithm can by concisely outlined
by the following items:
a) find the starting point and number all the
black pixels in succession.
b) create d-number of FSNNs.
c) train all FSNNs. For the i-th network, the
training set
,)}(,{
1
0
−
=
P
k
ik
kxu
where i=1,2,...,d is used.
d) blacken appropriate pixels and run
interpolation, if applicable.
Thanks to numbering the pixels as proposed,
networks are taught the functions which include no
violent changes. The property of periodicity of
FSNNs makes this type of networks to be very well
suitable for the purpose considered. The other
advantages of FSNNs, as listed in the introduction,
are also of great importance. It is worth to mention
that due to application of the method proposed, the
lossy compression of the closed curve is attained
because the number of FSNN’s weights is most
often much less than the number of pixels of the
curve under consideration. By changing the number
of FSNN’s neurons, we can modify the degree and
the quality of the compression.
Below, there are results from training FSNNs to
reconstruct the curve shown in Figure 1. The pixel in
the left-hand upper corner of this figure has the
coordinates (0,0) while the pixel in the right-hand
bottom corner has the coordinates (174,94). Figures
2a and 2b show reproduced shape of the curve from
Figure 1 for N=10 and N=30, respectively. During
computer simulations, it was assumed that
a
0
=0,a
1
=1,…,a
N
=N and b
1
=1,b
2
=2,…,b
N
=N. The
results shown are those without interpolation. The
cost function (3) was minimized.
Figure 2: Reconstructed shape of the curve shown in
Figure 1 a) for N=10, b) for N=30.
The method presented may be also applied to
train FSNNs the shape of a closed curve with added
line, e.g. the tank with an appended antenna as
shown in Figure 3. However, the reconstructed
image would be deformed by Gibbs effect, which
will occur due to stepwise change of at least one co-
ordinate value for pixels with successive numbers.
Figs. 5 and 6 provide results attained for the
proposed method used to map the closed curves
TRAINING FOURIER SERIES NEURAL NETWORKS TO MAP CLOSED CURVES
527

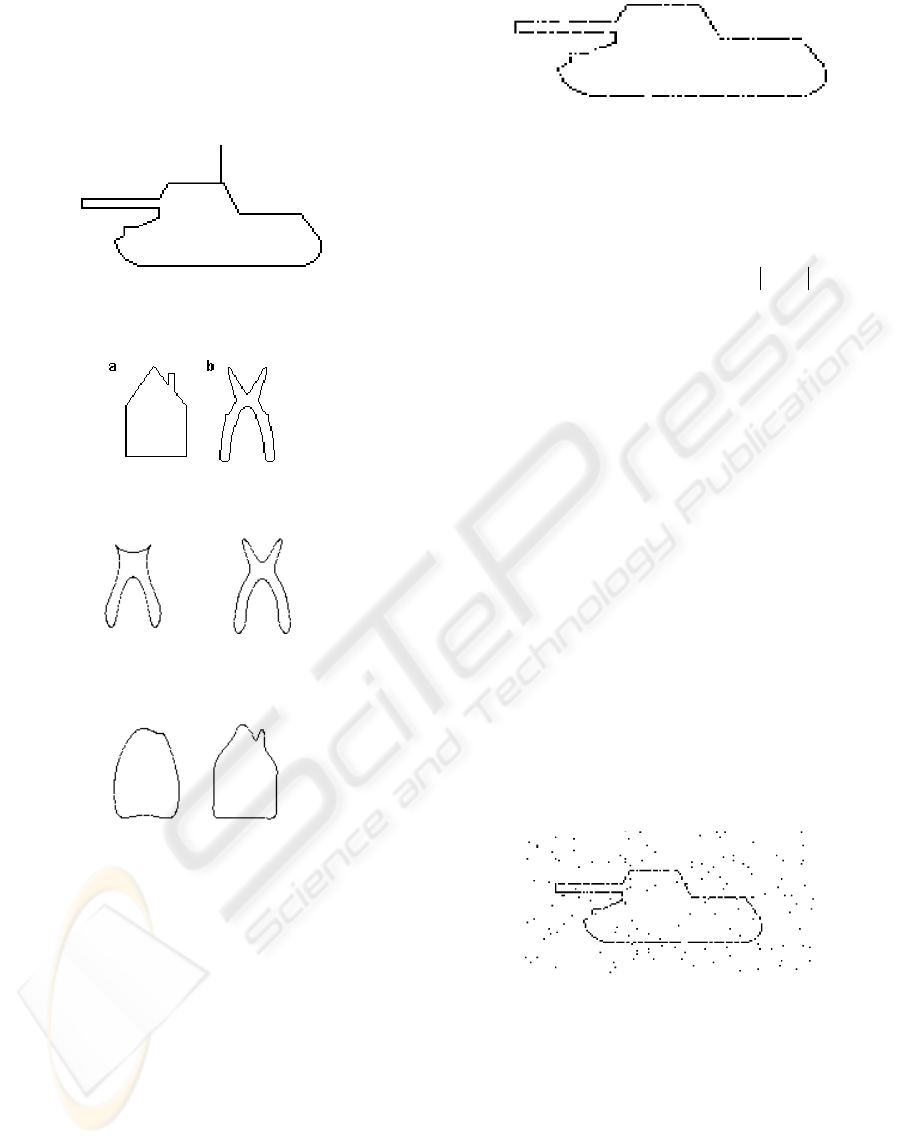
illustrated in Fig. 4. These curves were selected to
get clear indication of distinctive features of the
resulting mapping. For the sake of limited volume of
the paper no further experimental results are
presented.
Figure 3: The tank from Figure 1 with an appended
antenna.
Figure 4: The closed curves a) house b) pliers.
Figure 5: Reconstructed shape of the closed curve shown
in Figure 4b for N=5 and for N=10.
Figure 6: Reconstructed shape of the closed curve shown
in Figure 4a for N=5 and for N=10.
3 TRAINING FSNNS TO MAP
CLOSED CURVES FROM
IMAGES WHERE SOME
PIXELS WERE NOT MARKED
OUT
It is enough to introduce minor modifications in the
situation when we have the closed curve picture
where not all pixels were marked out of this curve.
An example of such image is shown in Figure 7.
Further in this paper, an assumption is made that
the distance between two points is counted by means
of norm L
1
(i.e. the so called Manhattan distance,
Figure 7: Picture of the closed curve where not all pixels
of this curve are marked.
called also the taxicab distance). For instance, let’s
assume that the points w and q have the coordinates
w
1
,w
2
,...,w
d
and q
1
,q
2
,...,q
d
, respectively. Then, the
distance between them equals to
∑
=
−
d
i
ii
qv
1
. In the
situation under discussion, at first all the pixels shall
be interconnected so as the sum of lengths of all
connections was the shortest and so that these
connections do not cross each other. Modification of
the method consists in a change of pixel numbering
way and assuming that the value P equals to the sum
of lengths of all created connections. Natural
numbers are assigned to the pixels and these
numbers are the distances from the starting pixel
counted along the route created by determined
connections. Let’s note that these would not always
be the successive natural numbers.
4 TRAINING FSNNS TO MAP
CLOSED CURVES FROM
DISTURBED PICTURES
Figure 8 illustrates an example of a picture with
closed curve disturbances where not all pixels
related to this curve are marked out.
Figure 8: Picture with disturbances of the closed curve
where not all pixels of this curve are marked out.
In situations similar to the case shown in Fig. 8, the
picture may be first divided into smaller parts of
identical dimensions.
Then, for each portion including the number of
marked out pixels higher than r, where r is
sufficiently large natural number selected according
to a priori knowledge about disturbances, the
average coordinates for all points belonging to the
specific portion are calculated. These averages are
IJCCI 2009 - International Joint Conference on Computational Intelligence
528

then treated as the coordinates of pixels creating the
image of closed curve with not all pixels of this
curve being marked out. Then, the procedure
outlined in Section 3 is used.
Figure 9: Figure 8 divided into smaller portions.
5 COMPARISON WITH SOME
OTHER METHODS
A mapping method for closed curves using Fourier
series is presented in (Ünsalan, 1998). This method
makes use of polar/spherical coordinates. However,
it is inapplicable when the radius is not a function,
i.e. the same value of the turning angle may
correspond to several different radius values. This
constitutes its essential drawback which drastically
reduces the number of closed curves which can be
mapped. The method outlined in (Ünsalan, 1998) is
applicable to map the curve shown in Fig. 4a but it
may not be directly applied to map the curves shown
in Figs 1 and 4b. The method presented in this paper
is free of that drawback. The method proposed by
the author has several similar advantages as that
given in (Ünsalan, 1998), e.g. it requires less
calculations than the 3L fit method (3LF) (Lei
1996). A valuable virtue of the proposed method is
the fact that upon teaching FSNNs, we always attain
the shape of closed curve which is not always a case
when implicit polynomials are used with the
methods of least squares fit (LSF), bounded least
squares fit (BLSF) and 3L fit (Lei, 1996). The LSF,
BLSF and 3LF methods are suitable for situation
described in Section 3. If it is a priori known that the
closed curve is given by equation of geometrical
figure or shape, better results could be reached by
specific-shape-dedicated methods, e.g. the method
presented in (Pilu, 1996).
6 CONCLUSIONS
The presented method is well-suited for
approximating closed curves. These curves may be
presented on a monochromatic picture. The FSNNs,
thanks to the property (2) and essential advantages
listed in Section 1, are especially suitable for
described purpose. As the problem size rises, it is
enough to increase the number of FSNNs used. The
FSNNs are taught the functions which include no
rapid changes. The presented method may be used
for the lossy compression of closed curves. It may
be also used to find the shape of closed curves out of
disturbed or incomplete pictures.
ACKNOWLEDGEMENTS
The author would like to thank the anonymous
reviewers for their comments, which improved the
paper
REFERENCES
Zhu C, Shukla D, Paul F.W., 2002, Orthogonal Functions
for System Identification and Control, In Control and
Dynamic Systems: Neural Network Systems
Techniques and Applications, Vol. 7, pp. 1-73 edited
by: Leondes C.T., Academic Press, San Diego
Sher C.F, Tseng C.S. and Chen C.S., 2001, Properties and
Performance of Orthogonal Neural Network in
Function Approximation, International Journal of
Intelligent Systems, Vol. 16, No. 12, pp. 1377-1392
Tseng C.S., Chen C.S., 2004, Performance Comparison
between the Training Method and the Numerical
Method of the Orthogonal Neural Network in Function
Approximation, International Journal of Intelligent
Systems, Vol. 19, No.12, pp. 1257-1275
Rafajłowicz E., Pawlak M., 1997, On Function Recovery
by Neural Networks Based on Orthogonal Expansions,
Nonlinear Analysis, Theory and Applications, Vol. 30,
No. 3, pp. 1343-1354, Proc. 2nd World Congress of
Nonlinear Analysis, Pergamon Press
Groß J., 2003, Linear Regression, Springer-Verlag, Berlin
Halawa K., 2008, Determining the Wegihts of a Fourier
Series Neural Network on the Basis of
Multidimensional Discrete Fourier Transform,
International Journal of Applied Mathematics and
Computer Science, Vol. 18, No. 3, pp. 369–375
Ünsalan C., Erçil A., 1998, Fourier Series Representation
For Implicit Polynomial Fitting, Bogazici Universitesi
Research Report, FBE-IE-08/98-09
Lei, Z., Blane, M.M., Cooper, D.B., 1996, 3L Fitting of
Higher Degree Implicit Polynomials, Proceedings of
the 3rd IEEE Workshop on Applications of Computer
Vision (WACV '96), pp. 148-153
Pilu M., Fitzgibbon A.W., Fisher R.B., 1996, Proceedings
of IEEE International Conference on Image
Processing, Vol 3, pp. 599-602
TRAINING FOURIER SERIES NEURAL NETWORKS TO MAP CLOSED CURVES
529