
A NOVEL TECHNIQUE FOR IRIS RECOGNITION SYSTEM
Kamal Vahdati Bana
Day System Evaluation and Research Institute
Amin Rezaeian Delui
Toos Institute of Higher Education, Mashhad, Iran
Amir Azizi
Eqbal Institute of Higher Education, Mashhad, Iran
Keywords: Biometric, Iris Recognition, Contourlet Transform, Co-occurrence matrix.
Abstract: In this paper we propose a new feature extraction method for iris recognition based on contourlet transform.
Contourlet transform captures the intrinsic geometrical structures of iris image. It decomposes the iris image
into a set of directional sub-bands with texture details captured in different orientations at various scales so
for reducing the feature vector dimensions we use the method for extract only significant bit and
information from normalized iris images. In this method we ignore fragile bits. At last, the feature vector is
created by using Co-occurrence matrix properties. For analyzing the desired performance of our proposed
method, we use the CASIA dataset, which is comprised of 108 classes with 7 images in each class and each
class represented a person. And finally we use SVM and KNN classifier for approximating the amount of
people identification in our proposed system. Experimental results show that the proposed increase the
classification accuracy and also the iris feature vector length is much smaller versus the other methods.
1 INTRODUCTION
The purpose of ‘Iris Recognition’, a biometrical
based technology for personal identification and
verification, is to recognize a person from his/her iris
prints. In fact, iris patterns are characterized by high
level of stability and distinctiveness. Various iris
recognition methods have been proposed for
automatic personal identification and verification. In
Figure.2 you can see the typical stages of Iris
Recognition system. Daugman first presented a
prototype system (
Daugman, J., 1993, 2004) for iris
recognition based on multi-scale Gabor wavelets.
Wildes presented another iris recognition system
(
Wildes, R. P, 1996, et al) in which the iris pattern was
decomposed into multi-resolution pyramid layers
using wavelet transform. Both systems of Daugman
and Wildes employed carefully designed image
acquisition devices to get equal high quality iris
images. Zhenan presented a shift-invariant method
(
Zhenan Sun et al., 2005) which decomposed the iris
pattern into multiple bands using a two-dimensional
Gabor filter. Boles & B.Boashash (
Boles W.W and
Boashash B, 1998
) decomposed one-dimensional
intensity signals computed on circles in the iris and
use zero-crossings of the decomposed signals for the
feature representation. Section 2 deals with Iris
Recognition System overview. Section 3 deals with
Experimental results and discussion. Section 4
concludes this paper.
2 IRIS RECOGNITION SYSTEM
OVERVIEW AND PROPOSED
METHOD
Figure 1 illustrates the main steps of our proposed
Approach. First the image preprocessing step
performs the localization of the pupil, detects the iris
530
Vahdati Bana K., Rezaeian Delui A. and Azizi A. (2009).
A NOVEL TECHNIQUE FOR IRIS RECOGNITION SYSTEM.
In Proceedings of the International Joint Conference on Computational Intelligence, pages 530-533
DOI: 10.5220/0002282805300533
Copyright
c
SciTePress
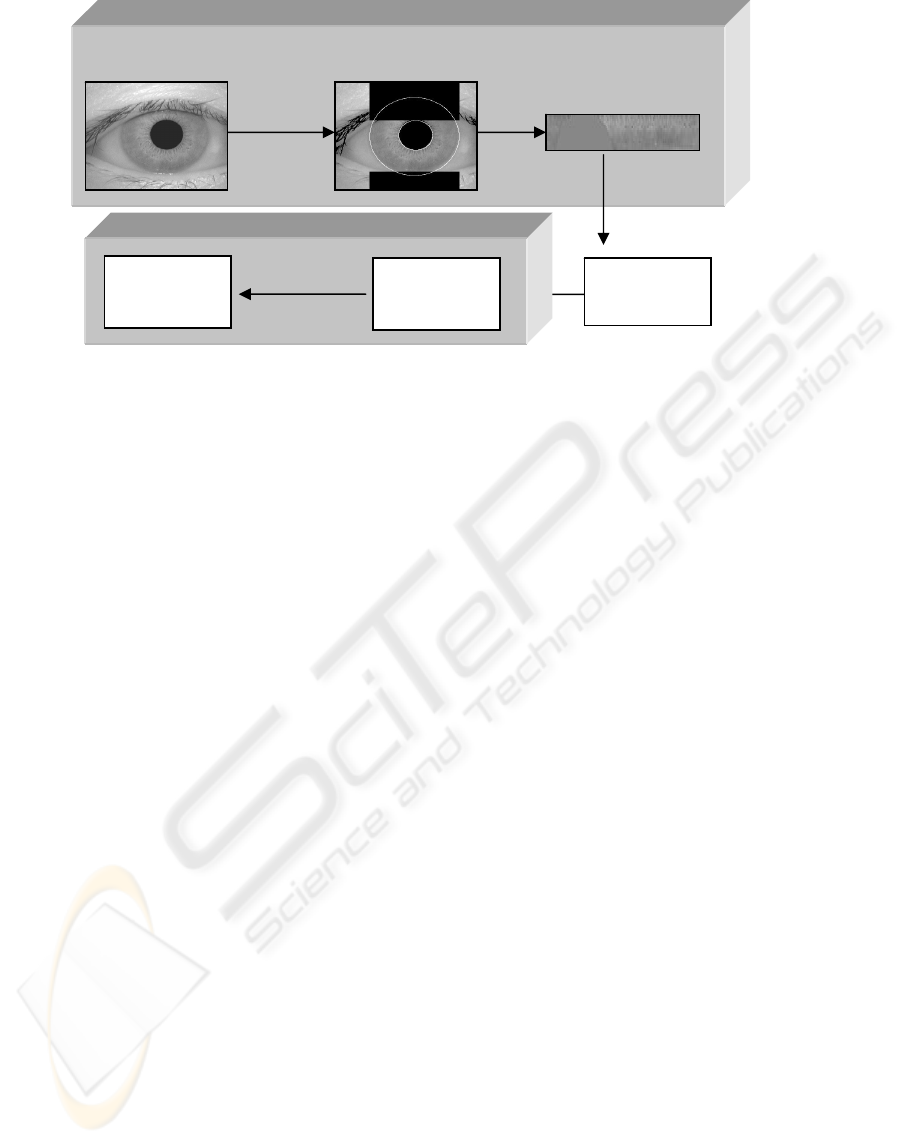
Figure 1: Flow diagram of the proposed iris recognition scheme.
boundary, and isolates the collarette region, which is
regarded as one of the most important areas of the
iris complex pattern. The collarette region is less
sensitive to the pupil dilation and usually unaffected
by the eyelids and the eyelashes we also detect the
eyelids and the eyelashes, which are the main
sources of the possible occlusion. In order to achieve
the invariance to the translation and the scale, the
isolated annular collarette area is transformed to a
rectangular block of fixed dimension. The
discriminating features are extracted from the
transformed image and the extracted features are
used to train the classifiers. The optimal features
subset is selected using several methods to increase
the matching accuracy based on the recognition
performance of the classifiers.
2.1 Feature Extraction and Encoding
Only the significant features of the iris must be
encoded so that comparisons between templates can
be made. Gabor filter and wavelet are the well-
known techniques in texture analysis (
Ma, L, et al.,
2002, 2003)
(Daugman, J., 1993, 2004)
(
Zhu, Y. et al., 2000) In wavelet family, Haar wavelet
(
Jafar M. H. Ali, Aboul Ella Hussanien, 2003) was
applied by Jafer Ali to iris image and they extracted
an 87-length binary feature vector. The major
Drawback of wavelets in two-dimensions is their
limited ability in capturing directional information.
The contourlet transform is a new extension of the
wavelet transform in two dimensions using multi-
scale and directional filter banks. The feature
representation should have enough information to
classify various irises and be less sensitive to noises.
Also in the most appropriate feature extraction we
attempt to extract only significant information,
moreover reducing feature vector dimensions.
Therefore the processing lessened and enough
information is supplied to introduce iris feature
vectors classification.
2.1.1 Contourlet Transform
Contourlet transform (CT) allows for different and
flexible number of directions at each scale. CT is
constructed by combining two distinct
decomposition stages (
Do M. N., and Vetterli, M,
2004)
, a multi-scale decomposition followed by
directional decomposition. The grouping of wavelet
coefficients suggests that one can obtain a sparse
image expansion by applying a multi-scale
transform followed by a local directional transform.
It gathers the nearby basis functions at the same
scale into linear structures. In essence, a wavelet-like
transform is used for edge (points) detection, and
then a local directional transform for contour
segments detection. A double filter bank structure is
used in CT in which the Laplacian pyramid (LP)
(
Burt P. J and Adelson E. H, 1983) is used to capture
the point discontinuities, and a directional filter bank
(DFB) (
Bamberger R.H and Smith M. J. T, 1992) to link
point discontinuities into linear structures.
2.1.2 The Best Bits in an Iris Code
Iris biometric systems apply filters to iris images to
extract information about iris texture. Daugman’s
approach maps the filter output to a binary iris code.
Iris Code
Iris Image Pre Processing
Segmentation Normalization
Classification
Classification
11011011010
00101010101
11100011100
Feature
Comparison
Similarity
Value
Feature Extraction
A NOVEL TECHNIQUE FOR IRIS RECOGNITION SYSTEM
531

The fractional Hamming distance between two iris
codes is computed and decisions about the identity
of a person are based on the computed distance. The
fractional Hamming distance weights all bits in an
iris code equally. However, not all the bits in an iris
code are equally useful. For a given iris image, a bit
in its corresponding iris code is defined as “fragile”
if there is any substantial probability of it ending up
a 0 for some images of the iris and a 1 for other
images of the same iris.According to (
Karen P.
Hollingsworth, Kevin W. Bowyer, 2008) the percentage
of fragile bits in each row of the iris code, Rows in
the middle of the iris code (rows 5 through 12) are
the most consistent.
2.1.3 Feature Vector in Proposed Method
In our method we use the Grey Level Co-occurrence
Matrix (GLCM). The technique uses the GLCM
(Grey Level Co-occurrence Matrix) of an image and
it provides a simple approach to capture the spatial
relationship between two points in a texture pattern.
It is calculated from the normalized iris image using
pixels as primary information. Various textural
features have been defined based on the work done
by Haralick [Haralick, R.M, et al., 1973]. These
features are derived by weighting each of the co-
occurrence matrix values and then summing these
weighted values to form the feature value. The
specific features considered in this research are
defined as follows:
1) Energy
=
∑∑
ij
jip
2
),(
2) Contrast
=
∑∑∑
−
===
⎥
⎦
⎤
⎢
⎣
⎡
=−
1
011
2
),(
ggg
N
n
N
i
N
j
njijiPn
3) Correlation =
yx
ij
yx
jiPij
σσ
μμ
∑∑
−),()(
4) Homogeneity=
∑∑
−+
ij
jiP
ji
),(
)(1
1
2
5) Autocorrelation =
∑∑
ij
jiPij ),()(
6) Dissimilarity =
∑∑
−
ij
jiPji ),(.
7) Inertia =
∑
∑
−
ij
jiPji ),()(
2
Here
yxyx
σ
σ
μ
μ
,,,
are mean and standard
deviation along x and y axis.
3 EXPERIMENTAL RESULTS
For creating iris feature vector we carried out the
following steps:
1) Iris normalized image (Rows in the middle
of the iris code (rows 5 through 12)) is
decomposed up to level two.(for each
image ,at level one , 2 and at level two , 4
sub band are created ) .
2) The sub bands of each level are put
together, therefore at level one a matrix
with 4*120 elements, and at level two a
matrix with 16*120 elements is created. We
named these matrixes: Matrix1 and Matrix
2.
3) By putting together Matrix1 and Matrix 2, a
new matrix named Matrix3 with 20*120
elements is created. The co-occurrence of
these three matrixes with offset one pixel
and angles 0, 45, 90 degree is created and
name this matrix: CO1, CO2 and CO3.in
this case for each image 3 co-occurrence
matrixes with 8*8 dimensions are created.
4) According to the Haralick‘s theory the co-
occurrence matrix has 14 properties , of
which in iris biometric system we used 7
properties which are used for 3 matrixes ,
so the feature vector is as follow:
F=[En1,Cont1,cor1,hom1,Acor1,dis1,ine1,
En2,Cont2,cor2, hom2,Acor2,dis2,ine2
En3,Cont3,cor3,hom3,Acor3,dis3,ine3]
In other word the feature vector in our method has
only 21 elements. Also for improving results, for
each sub bands and scale we create a feature vector
by using GLCM.in other words for each eight sub
bands in level 3 of Contourlet transform we
computed GLCM properties, separately and then by
combining these properties the feature vector is
created. In this case the feature vector has 56
elements. In Table 1 you can see the result of
implementing our proposed method:
IJCCI 2009 - International Joint Conference on Computational Intelligence
532

Table 1: Result of Implementing Proposed Method.
The
Number Of
Classes
The Correct of Percentage Classification (%)
KNN
Classifier
SVM
Classifier(Kernel
1)
SVM
Classifier(Kernel
2)
20 96.6 100 100
40 88.3 94.3 96.3
60 90.8 91.6 95.6
80 89.3 90.1 95.8
100(GLCM) 88.5 90.07 94.2
100(GLCM
(Combining
Sub bands)
87.5 91.3 96.3
4 CONCLUSIONS
In this paper we proposed an effective algorithm for
iris feature extraction using contourlet transform Co-
occurrence Matrix have been presented. The GLCM
proved to be a good technique as it provides
reasonable accuracy and is invariant to iris rotation.
For Segmentation and normalization we use
Daugman methods .Feature extraction in our
proposed method includes: sub bands proper
composition from Contuorlet pyramid and co-
occurrence calculations and finally selecting a set of
Haralick‘s properties that form the Maximum
distance between inter classes and Minimum
distance between intra classes. Our proposed method
can classify iris feature vector properly. The rate of
expected classification for the fairly large number of
experimental date in this paper verifies this claim. In
the other words our method provides a less feature
vector length with an insignificant reduction of the
percentage of correct classification.
REFERENCES
Bamberger, R.H., and Smith M. J. T, 1992. A filter bank
for the directional decomposition of images: Theory
and design, IEEE Trans. Signal Proc., vol. 40, no. 4,
pp. 882–893.
Boles, W.W., and Boashash B,1998.A Human
Identification Technique Using Images of the Iris and
Wavelet Transform, IEEE Trans. Signal Processing,
Vol.46, No.4, 1998, pp.1185-1188.
Burt P. J., and Adelson E. H., 1983. The Laplacian
pyramid as a compact image code, IEEE Trans.
Commun., vol. 31, no. 4, pp. 532–540.
Daugman, J., 1993. High confidence visual recognition of
persons by a test of statistical independence, IEEE
Transactions on Pattern Analysis and Machine
Intelligence, Vol. 15, No. 11, pp: 1148-1160.
Daugman, J., 2004. How Iris Recognition works.IEEE
Transactions on Circuits and systems for video
Technology, Vol.14, No.1, pp: 21-30.
Do M. N., and Vetterli, M, 2004. The contourlet
transform: an Efficient directional multi-resolution
image representation, IEEE Transactions on Image
Processing, vol. 14, issue 12, pp. 2091-2106.
Haralick, R.M, et al., 1973.Textural features for image
classification, IEEE Transactions on Systems, Man,
and Cybernetics, vol.3, no.6, and pp.610-621.
Karen P. Hollingsworth, Kevin W. Bowyer, 2008. The
Best Bits in an Iris Code, IEEE Transactions on
Pattern Analysis and Machine Intelligence (PAMI).
Ma, L, et al. 2003. Personal identification based on iris
texture analysis, IEEE Trans. Patt. Analy. & Mach.
Intel vol. 25, No. 12, pp. 1519-1533.
Sanchez-Avila, C. et al.,2002.Iris-based biometric
recognition using dyadic wavelet transform,IEEE
Aerospace and Electronics Systems Magazine ,
Volume: 17 Issue 10, pp. 3-6.
Wildes, R. P, 1996, et al., A machine-vision system for iris
recognition, Machine Vision and Applications,
Springer-Vela.
Zhenan Sun et al., 2005.Improving Iris Recognition
Accuracy via Cascaded Classifier, IEEE Transactions
on systems, Man and Cybernetics-part C: Applications
reviews, Vol.35, No.3.
CASIA, 2003.Chinese Academy of Sciences – Institute of
Automation, Database of 756 Grayscale Eye Images.
http://www.sinobiometrics.com Version 1.0.
Jafar M. H. Ali, Aboul Ella Hussanien,2003.An Iris
Recognition System to Enhance E-security
Environment Based on Wavelet Theory, AMO -
Advanced Modeling and Optimization, Volume 5,
Number 2.
Ma, L, et al., 2002. Iris Recognition Based on
Multichannel Gabor Filtering, Proc. Fifth Asian Conf.
Computer Vision, vol. I, pp. 279-283.
Zhu, Y. et al., 2000. Biometric Personal Identification
Based on Iris Patterns, Proc. Int’l Conf. Pattern
Recognition, vol. II,pp. 805-808.
A NOVEL TECHNIQUE FOR IRIS RECOGNITION SYSTEM
533
