REVERSE ENGINEERING AND SYMBOLIC KNOWLEDGE
EXTRACTION ON ŁUKASIEWICZ LOGICS USING NEURAL
NETWORKS
Carlos Leandro
´
Area Cientifica da Matem
´
atica, Instituto Superior de Engenharia de Lisboa
Instituto Polit
´
ecnico de Lisboa, Portugal
Keywords:
Fuzzy logics, Łukasiewicz logic, Reverse Engineering, Symbolic Knowledge Extraction, Neural Networks,
Link grammars, Levenderg-Marquardt algorithm, Optimal Brain Surgeon.
Abstract:
This work describes a methodology that combines logic-based systems and connectionist systems. Our ap-
proach uses finite truth-valued Łukasiewicz logic, where we take advantage of fact, presented in (Castro and
Trillas, 1998), wherein every connective can be defined by a neuron in an artificial network having, by acti-
vation function, the identity truncated to zero and one. This allowed the injection of formulas into a network
architecture, and also simplified symbolic rule extraction. Neural networks are trained using the Levenderg-
Marquardt algorithm, where we restricted the knowledge dissemination in the network structure, and the
generated network is simplified applying the ”Optimal Brain Surgeon” algorithm proposed by B. Hassibi, D.
G. Stork and G.J. Wolf. This procedure reduces neural network plasticity without drastically damaging the
learning performance, thus making the descriptive power of produced neural networks similar to the descrip-
tive power of Łukasiewicz logic language and simplifying the translation between symbolic and connectionist
structures. We used this method in the reverse engineering problem of finding the formula used on the gen-
eration of a given truth table. For real data sets the method is particularly useful for attribute selection, on
binary classification problems defined using nominal attributes, where each instance has a level of uncertainty
associated with it.
1 INTRODUCTION
There are essentially two representation paradigms,
usually taken very differently. On one hand,
symbolic-based descriptions are specified through a
grammar that has fairly clear semantics, can codify
structured objects, in some cases can support various
forms of automated reasoning, and can be transparent
to users. On the other hand, the usual way to see infor-
mation presented using a connectionist description is
its codification on a neural network. Artificial neural
networks (NNs), in principle, combine - among other
things - the ability to learn and robustness or insensi-
tivity to perturbations of input data. NNs are usually
taken as black boxes, thereby providing little insight
into how the information is codified. The knowledge
captured by NNs is not transparent to users and can-
not be verified by domain experts.
It is natural to seek a synergy integrating the
white-box character of symbolic base representation
and the learning power of artificial neuronal networks.
Such neuro-symbolic models are currently a very ac-
tive area of research see (Bornscheuer et al., 1998)
(Hitzler et al., 2004) (H
¨
olldobler, 2000) (H
¨
olldobler
and Kalinke, 1994) (H
¨
olldobler et al., 1999), for
the extraction of logic programs from trained net-
works. The extraction of modal and temporal logic
programs see (d’Avila Garcez, 2007) and (d’Avila
Garcez et al., 2008), for connectionist representation
of multi-valued logic programs see (Komendantskaya
et al., 2007) and (Eklund and Klawonn, 1992).
Our approach to neuro-symbolic models and
knowledge extraction is based on a comprehensive
language for humans, representable directly in a NN
topology and able to be used, like knowledge-based
networks (Fu, 1993) (Towell and Shavlik, 1994), to
generate the initial network architecture from crude
symbolic domain knowledge. In the other direction,
neural language can be translated into its symbolic
language like presented in (Gallant, 1988) (Gallant,
1994) (Towell and Shavlik, 1993). However this pro-
cesses has been used to identify the most significant
5
Leandro C. (2009).
REVERSE ENGINEERING AND SYMBOLIC KNOWLEDGE EXTRACTION ON ŁUKASIEWICZ LOGICS USING NEURAL NETWORKS.
In Proceedings of the International Joint Conference on Computational Intelligence, pages 5-16
DOI: 10.5220/0002283900050016
Copyright
c
SciTePress
determinants of decision or classification. This is a
hard problem since, often, an artificial NN with good
generalization does not necessarily imply involve-
ment of hidden units with distinct meaning. Hence,
any individual unit cannot essentially be associated
with a single concept or feature of the problem do-
main. This the archetype of connectionist approaches,
where all information is stored in a distributed man-
ner among the processing units and their associated
connectivity. However, in this work we used a propo-
sitional language wherein formulas are interpreted as
NNs. In this framework formulas are simple to inject
into a multilayer feed-forward network, and we are
free from the need of giving interpretation to hidden
units in the problem domain.
For this task we selected the propositional lan-
guage of Łukasiewicz logic. This type of multi-
valued logic has a very useful property motivated by
the ”linearity” of logic connectives. Every logic con-
nective can be defined by a neuron in an artificial
network having, by activation function, the identity
truncated to zero and one (Castro and Trillas, 1998).
This allows the direct codification of formulas in the
network architecture, and simplifies the extraction of
rules. Multilayer feed-forward NN, having this type
of activation function, can be trained efficiently us-
ing the Levenderg-Marquardt algorithm (Hagan and
Menhaj, 1999), and the generated network can be
simplified using the ”Optimal Brain Surgeon” algo-
rithm proposed by B. Hassibi, D. G. Stork and G.J.
Stork (Hassibi et al., 1993).
This strategy has good performance when applied
to the reconstruction of formulas from truth tables.
If the truth table is generated using a formula from
the Łukasiewicz propositional logic language, the op-
timum solution is defined using only units directly
translated into formulas. In this type of reverse engi-
neering problem, we presuppose no noise. However,
the process is stable for the introduction of Gaussian
noise into the input data. This motivates its applica-
tion to extract comprehensible symbolic rules from
real data. However, often a model with good gen-
eralization can be described using configuration of
neural units without exact symbolic presentation. We
describe, in the following, a simple rule to generate
symbolic approximation for un-representable config-
urations.
Our method has good performance for attribute se-
lection from real data. We used it for data set sim-
plification, removing potentially irrelevant attributes.
This reduces the problem dimension, reducing the
size of neuronal network to be trained.
2 PRELIMINARIES
We begin by presenting the basic notions we need
from the subjects of many-valued logics, and by
showing how formulas in a propositional language
can be injected into and extracted from a feed-forward
NN.
2.1 Łukasiewicz Logics
Classical propositional logic is one of the earliest for-
mal systems of logic. The algebraic semantics of this
logic are given by Boolean algebra. Both, the logic
and the algebraic semantics have been generalized in
many directions. The generalization of Boolean alge-
bra can be based in the relationship between conjunc-
tion and implication given by
(x∧y)≤z⇔x≤(y→z)⇔y≤(x→z).
(1)
These equivalences, called residuation equivalences,
imply the properties of logic operators in Boolean al-
gebras. They can be used to present implication as a
generalized inverse for conjunction.
In applications of fuzzy logic, the properties of
Boolean conjunction are too rigid, hence it is ex-
tended a new binary connective, ⊗, which is usually
called fusion. Extending the commutativity to the fu-
sion operation, the residuation equivalences define an
implication denoted in this work by ⇒ :
(x⊗y)≤z⇔x≤(y⇒z)⇔y≤(x⇒z).
(2)
These two operators are defined in a partially ordered
set of truth values, (P,≤), thereby extending the two-
valued set of an Boolean algebra. This defines a resid-
uated poset (P,⊗,⇒,≤), where we interprete P as a
set of truth values. This structure has been used in the
definition of many types of logics. If P has more than
two values, the associated logics are called a many-
valued logics.
We focused our attention on many-valued logics
having [0,1] as set of truth values. In this type of
logics the fusion operator ⊗ is known as a t-norm.
In (Gerla, 2000), it is described as a binary opera-
tor defined in [0,1] commutative and associative, non-
decreasing in both arguments, 1⊗x = x and 0⊗x = 0.
The following are example of continuous t-norms:
1. Łukasiewicz t-norm: x ⊗y = max(0,x +y −1).
2. Product t-norm: x ⊗y = xy usual product between
real numbers.
3. G
¨
odel t-norm: x ⊗ y = min(x, y).
In (Frank, 1979), all continuous t-norms are charac-
terized using only Łukasiewicz, G
¨
odel and product t-
norms.
IJCCI 2009 - International Joint Conference on Computational Intelligence
6
Figure 1: Saturating linear transfer function.
Many-valued logics can be conceived of as a set
of formal representation languages that have proven
to be useful for both real-world and computer sci-
ence applications. When they are defined by con-
tinuous t-norms they are known as fuzzy logics.
The fuzzy logic defined using Łukasiewicz t-norm
is called Łukasiewicz logic and the corresponding
propositional calculus has a nice complete axiomati-
zation (H
´
ajek, 1995).
2.2 Processing Units
As mentioned in (Amato et al., 2002) there is a lack of
a deep investigation of the relationships between log-
ics and NNs. In this work we present a methodology
using NNs to learn formulas from data.
In (Castro and Trillas, 1998) it is shown how, by
taking as activation function, ψ, the identity truncated
to zero and one,
ψ(x)=min(1,max(x,0)),
(3)
it is possible to represent the corresponding NN as a
combination of propositions of Łukasiewicz calculus
and viceversa (Amato et al., 2002).
In Łukasiewicz logic sentences are usually built
from a (countable) set of propositional variables, a
conjunction ⊗ (the fusion operator), an implication
⇒, and the truth constant 0. Further connectives are
defined as follows:
1. ¬ϕ
1
is ϕ
1
⇒ 0
2. ϕ
1
⊕ ϕ
2
is ¬ϕ
1
⇒ ϕ
2
,
3. ϕ
1
∧ ϕ
2
is ϕ
1
⊗ (ϕ
1
⇒ ϕ
2
),
4. ϕ
1
∨ ϕ
2
is ((ϕ
1
⇒ ϕ
2
) ⇒ ϕ
2
) ∧ ((ϕ
2
⇒ ϕ
1
) ⇒ ϕ
1
)
5. ϕ
1
⇔ ϕ
2
is (ϕ
1
⇒ ϕ
2
) ⊗ (ϕ
2
⇒ ϕ
1
)
6. 1 is 0 ⇒ 0
The interpretation for a well-formed formula ϕ
is defined by assigning a truth value to each propo-
sitional variable. However, if we want to apply a
NN in order to learn Łukasiewicz sentences, it seems
more promising if we take a non-recursive approach
to proposition evaluation. We can do this by defining
the language as a set of molecular components gen-
erated from the plugging of atomic components. For
this, we used the library of components presented in
figure 2, interpreted as neural units and linked them
together, to form NNs having only one output, with-
out loops. These NNs are interpretation for formu-
las, having its structure where each neuron defines the
connective identified by its label. This task of con-
struct complex structures based on simplest ones can
be formalized using generalized programming (Fi-
adeiro and Lopes, 1997).
In other words the language for Łukasiewicz logic
is defined by the set of all NNs, wherein neurons as-
sume one of the configurations presented in figure 2.
x
1
@
@
−1
'&%$ !"#
⊗
y
1
x
−1
C
C
1
'&%$ !"#
⇒
y
1
|
|
|
x
1
@
@
0
'&%$ !"#
⊕
y
1
x
0
>
>
1

1
y
0
x
0
>
>
0

0
y
0
1
x
−1

¬
0
x
1

=
Figure 2: Neural networks codifying formulas x ⊗ y, x ⇒ y,
x ⊕ y, 1, 0, ¬x and x.
The neurons of these types of networks, which
have two inputs and one output, can be interpreted as
a function (see figure 3) and are generically denoted,
in the following, by ψ
b
(w
1
x
1
,w
2
x
2
), where b repre-
sent the bias, w
1
and w
3
are the weights and, x
1
and
x
2
input values. In this context a network is the func-
tional interpretation of a sentence in the string-based
notation when the relation, defined by network execu-
tion, corresponds to the sentence truth table.
x
w
1
=
=
b
'&%$ !"#
ψ
z ⇔ z = min(1, max(0, w
1
x + w
2
y + b))
y
w
2
= ψ
b
(w
1
x,w
2
y)
Figure 3: Functional interpretation for a neural network.
The use of NNs as interpretation of formulas sim-
plifies the transformation between string-based rep-
resentations and the network representation, allowing
one to write:
Proposition 1. Every well-formed formula in the
Łukasiewicz logic language can be codified using a
NN, and the network defines the formula interpreta-
tion, when the activation function is the identity trun-
cated to zero and one.
For instance, the semantic for sentence
ϕ=(x⊗y⇒z)⊕(z⇒w),
can be described using the bellow network or can be
codified by the presented set of matrices. From this
matrices we must note that the partial interpretation
REVERSE ENGINEERING AND SYMBOLIC KNOWLEDGE EXTRACTION ON AUKASIEWICZ LOGICS USING
NEURAL NETWORKS
7
of each unit can be seen as a simple exercise of pat-
tern checking, where we must take by reference rela-
tion between formulas and configuration described in
table 1.
x
1
B
B
B
−1
'&%$ !"#
⊗
−1
C
C
C
1
y
1
}
}
}

=
1
'&%$ !"#
⇒
1
B
B
B
0
z
−1
C
C
C
1
}
}
}
1
0
0
'&%$ !"#
⊕
'&%$ !"#
⇒
1

=
1
{
{
{
w
1
z
z
z
x y z w
b’s partial interpretation
i
1
i
2
i
3
1 1 0 0
0 0 1 0
0 0 −1 1
−1
0
1
x ⊗ y
z
z ⇒ w
i
1
i
2
i
3
j
1
j
2
−1 1 0
0 0 1
1
0
i
1
⇒ i
2
i
3
j
1
j
2
1 1
0
j
1
⊕ j
2
INTERPRETATION:
j
1
⊕ j
2
= (i
1
⇒ i
2
) ⊕ (i
3
) = ((x ⊗ y) ⇒ z) ⊕ (z ⇒ w)
In this sense this NN can be seen as an interpretation
for sentence ϕ; it codifies f
ϕ
, the proposition truth ta-
ble. This relationship is presented in string-base nota-
tion by writing:
f
ϕ
(x,y,z,w)=ψ
0
(ψ
0
(ψ
1
(−z,w)),ψ
1
(ψ
0
(z),−ψ
−1
(x,y)))
However truth table f
ϕ
is a continuous structure, for
our goal, it must be discretized using a finite structure,
ensuring sufficient information to describe the origi-
nal formula. A truth table f
ϕ
for a formula ϕ, in a
fuzzy logic, is a map f
ϕ
: [0,1]
m
→ [0, 1], where m is
the number of propositional variables used in ϕ. For
each integer n > 0, let S
n
be the set {0,
1
n
,...,
n−1
n
,1}.
Each n > 0, defines a sub-table for f
ϕ
defined by
f
(n)
ϕ
: (S
n
)
m
→ [0,1], given by f
(n)
ϕ
( ¯v) = f
ϕ
( ¯v), and
called the ϕ (n+1)-valued truth sub-table.
2.3 Similarity between a Configuration
and a Formula
We call a Castro neural network (CNN) a type
of NN having as activation function ψ(x) =
min(1,max(0,x)), where its weights are -1, 0 or 1 and
having by bias an integer. A CNN is called repre-
sentable if it is codified as a binary NN: i.e. a CNN
where each neuron has one or two inputs. A network
is called un-representable if is impossible to codify
using a binary CNN. In figure 4, we present the ex-
ample of an un-representable network configuration,
as we will see in the following.
Note that, a binary CNN can be translated directly
into Łukasiewicz logic language, using the correspon-
dences described in table 1; in this sense, we called
them Łukasiewicz neural network (ŁNN).
x
−1
?
?
?
0
y
1
?>=<89:;
ψ
w ⇔ w = ψ
0
(−x,y,z)
z
1
Figure 4: An un-representable neural network.
Table 1: Possible configurations for a neuron in a
Łukasiewicz neural network a its interpretation.
Formula: Configuration: Formula: Configuration:
¬x ⊕ y
x
−1
>
>
>
1

ϕ
y
1
x ⊗ ¬y
x
1
>
>
>
0

ϕ
y
−1
x ⊕ y
x
1
>
>
>
0

ϕ
y
1
¬x ⊗ ¬y)
x
−1
>
>
>
1

ϕ
y
−1
x ⊕ ¬y
x
1
>
>
>
1

ϕ
y
−1
x ⊗ y
x
1
>
>
>
−1

ϕ
y
1
¬x ⊗ y
x
−1
>
>
>
0

ϕ
y
1
¬x ⊕ ¬y
x
−1
>
>
>
2

ϕ
y
−1
Below we present functional interpretation for for-
mulas defined using a neuron with two inputs. These
interpretation are classified as disjunctive interpreta-
tions ou conjunctive interpretations.
Disjunctive interpretations Conjunctive interpretations
ψ
0
(x
1
,x
2
) = f
x
1
⊕x
2
ψ
−1
(x
1
,x
2
) = f
x
1
⊗x
2
ψ
1
(x
1
,−x
2
) = f
x
1
⊕¬x
2
ψ
0
(x
1
,−x
2
) = f
x
1
⊗¬x
2
ψ
1
(−x
1
,x
2
) = f
¬x
1
⊕x
2
ψ
0
(−x
1
,x
2
) = f
¬x
1
⊗x
2
ψ
2
(−x
1
,−x
2
) = f
¬x
1
⊕¬x
2
ψ
1
(−x
1
,−x
2
) = f
¬x
1
⊗¬x
2
These correspond to all possible configurations of
neurons with two inputs. The other possible config-
urations are constant and can also be seen as repre-
sentable configurations. For instance, ψ
b
(x
1
,x
2
) = 0,
if b < −1, and ψ
b
(−x
1
,−x
2
) = 1, if b > 1.
In this sense, every representable network can be
codified by a NN where the neural units satisfy one
of the above patterns. Below we can see also ex-
amples of representable configurations for a neuron
with three inputs. In the table we presente how they
can be codified using representable NNs having units
with two inputs, and the corresponding interpreting
formula in the sting-based notation.
Conjunctive configurations
ψ
−2
(x
1
,x
2
,x
3
) = ψ
−1
(x
1
,ψ
−1
(x
2
,x
3
)) = f
x
1
⊗x
2
⊗x
3
ψ
−1
(x
1
,x
2
,−x
3
) = ψ
−1
(x
1
,ψ
0
(x
2
,−x
3
)) = f
x
1
⊗x
2
⊗¬x
3
ψ
0
(x
1
,−x
2
,−x
3
) = ψ
−1
(x
1
,ψ
1
(−x
2
,−x
3
)) = f
x
1
⊗¬x
2
⊗¬x
3
ψ
1
(−x
1
,−x
2
,−x
3
) = ψ
0
(−x
1
,ψ
1
(−x
2
,−x
3
)) = f
¬x
1
⊗¬x
2
⊗¬x
3
IJCCI 2009 - International Joint Conference on Computational Intelligence
8
Disjunctive interpretations
ψ
0
(x
1
,x
2
,x
3
) = ψ
0
(x
1
,ψ
0
(x
2
,x
3
)) = f
x
1
⊕x
2
⊕x
3
ψ
1
(x
1
,x
2
,−x
3
) = ψ
0
(x
1
,ψ
1
(x
2
,−x
3
)) = f
x
1
⊕x
2
⊕¬x
3
ψ
2
(x
1
,−x
2
,−x
3
) = ψ
0
(x
1
,ψ
2
(−x
2
,−x
3
)) = f
x
1
⊕¬x
2
⊕¬x
3
ψ
3
(−x
1
,−x
2
,−x
3
) = ψ
1
(−x
1
,ψ
2
(−x
2
,−x
3
)) = f
¬x
1
⊕¬x
2
⊕¬x
3
Constant configurations like ψ
b
(x
1
,x
2
,x
3
) = 0, if b <
−2, and ψ
b
(−x
1
,−x
2
,−x
3
) = 1, if b > 3, are also
representable. However there are examples of un-
representable networks with three inputs like the con-
figuration presented in figure 4.
Naturally, a neuron configuration - when repre-
sentable - can by codified by different structures using
a ŁNN. Particularly, we have:
Proposition 2. If the neuron configuration
α = ψ
b
(x
1
,x
2
,...,x
n−1
,x
n
) is representable, but
not constant, it can be codified in a ŁNN with the
following structure:
α=ψ
b
1
(x
1
,ψ
b
2
(x
2
,...,ψ
b
n−1
(x
n−1
,x
n
)...)),
(4)
where
b
1
,b
2
,...,b
n−1
are integers, and
b=b
1
+b
2
+...+b
n−1
.
And, since the n-nary operator ψ
b
is commutative,
variables
x
1
,x
2
,...,x
n−1
,x
n
)
could interchange its position
in function
α=ψ
b
(x
1
,x
2
,...,x
n−1
,x
n
)
without changing the
operator output. By this we mean that, for a three
input configuration, when we permutate variables, we
generate equivalent configurations:
ψ
b
(x
1
,x
2
,x
3
)=ψ
b
(x
2
,x
3
,x
1
)=ψ
b
(x
3
,x
2
,x
1
)=...
(5)
When these are representa, they can be codified in
string-based notation using logic connectives. But
these diferente configuration only generate equiva-
lente formulas if these formulas are disjunctive ou
conjunctive formulas. A disjunctive formulas is for-
mula written using the disjunction of propositional
variables or negation of propositional variable. Simi-
larly, a conjunctive formulas are formulas written us-
ing only the conjunction of propositional variables or
its negation.
Proposition 3. If α = ψ
b
(x
1
,x
2
,...,x
n−1
,x
n
) is rep-
resentable, it is the interpretation of a disjunctive for-
mula or a conjunctive formula.
This leave us with the task of classifying a neuron
configuration according to its representation. For that,
we established a relationship using the configuration
bias and the number of negative and positive weights.
Proposition 4. (Dubois and Prade, 2000) Given the
neuron configuration
α=ψ
b
(−x
1
,−x
2
,...,−x
n
,x
n+1
,...,x
m
)
(6)
with m = n + p inputs and where n and p are, respec-
tively, the number of negative and the number of pos-
itive weights, on the neuron configuration:
1. If b = −p + 1 the neuron is called a conjunction
and it is a interpretation for
¬x
1
⊗...⊗¬x
n
⊗x
n+1
⊗...⊗x
m
.
(7)
2. When b = n the neuron is called a disjunction and
it is a interpretation of
¬x
1
⊕...⊕¬x
n
⊕x
n+1
⊕...⊕x
m
.
(8)
From the structure associated with this type of for-
mula, we proposed the following structural character-
ization for representable neurons:
Proposition 5. Every conjunctive or disjunctive con-
figuration α = ψ
b
(x
1
,x
2
,...,x
n−1
,x
n
), can be codified
by a ŁNN
β=ψ
b
1
(x
1
,ψ
b
2
(x
2
,...,ψ
b
n−1
(x
n−1
,x
n
)...)),
(9)
where
b=b
1
+b
2
+···+b
n−1
and b
1
≤b
2
≤···≤b
n−1
.
(10)
This property can be translated in the following
neuron rewriting rule,
w
1
8
8
8
8
b
.
.
.
'&%$ !"#
ψ
R
//
w
n
w
1
8
8
8
8
b
0
.
.
.
'&%$ !"#
ψ
1
7
7
7
7
b
1
w
n−1
'&%$ !"#
ψ
w
n
n
n
n
n
n
n
linking equivalent networks, when values b
0
and b
1
satisfy b = b
0
+ b
1
and b
1
≤ b
0
, and are such that
neither of the involved neurons have constant output.
This rewriting rule can be used to join equivalent con-
figurations like:
x
−1
@
@
@
2
y
1

ϕ
R
//
z
−1
w
1
x
−1
@
@
@
2
y
1

ϕ
1
>
>
>
0
R
//
z
−1

ϕ
w
1
o
o
o
o
o
x
−1
@
@
@
2
z
−1

ϕ
1
>
>
>
0
y
1
76540123
ϕ
1
>
>
>
0
w
1

ϕ
Note that, a representable CNN can be transformed
by the application of rule R in a set of equivalent ŁNN
with simplest neuron configuration. Then we have:
Proposition 6. Un-representable neuron configura-
tions are those transformed by rule R in, at least, two
non-equivalent NNs.
For instance, the un-representable configuration
ψ
0
(−x
1
,x
2
,x
3
), presented in figure 4, is transformed
by rule R in three non-equivalent configurations:
1. ψ
0
(x
3
,ψ
0
(−x
1
,x
2
)) = f
x
3
⊕(¬x
1
⊗x
2
)
,
2. ψ
−1
(x
3
,ψ
1
(−x,x
2
)) = f
x
3
⊗(¬x
1
⊗x
2
)
, or
3. ψ
0
(−x
1
,ψ
0
(x
2
,x
3
)) = f
¬x
1
⊗(x
2
⊕x
3
)
.
The representable configuration ψ
2
(−x
1
,−x
2
,x
3
) is
transformed by rule R on only two distinct but equiv-
alent configurations:
REVERSE ENGINEERING AND SYMBOLIC KNOWLEDGE EXTRACTION ON AUKASIEWICZ LOGICS USING
NEURAL NETWORKS
9
1. ψ
0
(x
3
,ψ
2
(−x
1
,−x
2
)) = f
x
3
⊕¬(x
1
⊗x
2
)
, or
2. ψ
1
(−x
2
,ψ
1
(−x
1
,x
3
)) = f
¬x
2
⊕(¬x
1
⊕x
3
)
From this case we can concluded that CNNs have
more expressive power than Łukasiewicz logic lan-
guage. Since there are structures defined using CNNs
but not codified in the Łukasiewicz logic language.
For the extraction of knowledge from trained NNs,
we translate neuron configuration in propositional
connectives to form formulas. However, not all neu-
ron configurations can be translated in formulas, but
they can be approximate by formulas. To quantify the
approximation quality we defined the notion of inter-
pretation λ-similar to a formula.
Two neuron configurations α = ψ
b
(x
1
,x
2
,...,x
n
)
and β = ψ
b
0
(y
1
,y
2
,...,y
n
), are called λ-similar, in a
(m + 1)-valued Łukasiewicz logic, if λ is the expo-
nential of mean absolute error symmetric, evaluated
taking the same cases in the truth sub-table of α and
β. When we have
λ = e
−
∑
¯x∈T
|α( ¯x)−β( ¯x)|
]T
,
(11)
write α ∼
λ
β. If α is un-representable and β is rep-
resentable, the second configuration is called a repre-
sentable approximation to the first.
On the 2-valued Łukasiewicz logic (the Boolean
logic case), we have for the un-representable configu-
ration α = ψ
0
(−x
1
,x
2
,x
3
):
1. ψ
0
(−x
1
,x
2
,x
3
) ∼
0.883
ψ
0
(x
3
,ψ
0
(−x
1
,x
2
)),
2. ψ
0
(−x
1
,x
2
,x
3
) ∼
0.883
ψ
−1
(x
3
,ψ
1
(−x
1
,x
2
)), and
3. ψ
0
(−x
1
,x
2
,x
3
) ∼
0.883
ψ
0
(−x
1
,ψ
0
(x
2
,x
3
)).
In this case, the truth sub-tables of, formulas α
1
=
x
3
⊕(¬x
1
⊗x
2
), α
1
= x
3
⊗(¬x
1
⊗x
2
) and α
1
= ¬x
1
⊗
(x
2
⊕ x
3
) are both λ-similar to ψ
0
(−x
1
,x
2
,x
3
), where
λ = 0.883, since they differ in one position on 8 pos-
sible positions. This means that both formulas are
87.5% accurate. The quality of this approximations
was checked analyzing the similarity level λ on oth-
ers finite Łukasiewicz logics. In every selected logic
formula α
1
,α
2
and α
3
had the some similarity level
when compared to α:
• 3-valued logic, λ = 0.8779, 4-valued logic, λ = 0.8781,
• 5-valued logic, λ = 0.8784, 10-valued logic, λ = 0.8798,
• 20-valued logic, λ = 0.8809, 30-valued logic, λ = 0.8814,
• 50-valued logic, λ = 0.8818.
For a more complex configuration like α =
ψ
0
(−x
1
,x
2
,−x
3
,x
4
,−x
5
), we can derive, using rule
R, configurations:
1. β
1
= ψ
0
(−x
5
,ψ
0
(x
4
,ψ
0
(−x
3
,ψ
0
(x
2
,−x
1
))))
2. β
2
= ψ
−1
(x
4
,ψ
−1
(x
2
,ψ
0
(−x
5
,ψ
0
(−x
3
,−x
1
))))
3. β
3
= ψ
−1
(x
4
,ψ
0
(−x
5
,ψ
0
(x
2
,ψ
1
(−x
3
,−x
1
))))
4. β
4
= ψ
−1
(x
4
,ψ
0
(x
2
,ψ
0
(−x
5
,ψ
1
(−x
3
,−x
1
))))
Since these configurations are not equivalents, we
concluded that α is un-representable. In this case we
can see a change in the similarity level between α and
each β
i
when the number of truth valued is changed:
• In the 2-valued logic α ∼
0.8556
β
1
, α ∼
0.9103
β
2
, α ∼
0.5189
β
3
and α ∼
0.5880
β
4
;
• In the 3-valued logic α ∼
0.8746
β
1
, α ∼
0.9213
β
2
, α ∼
0.4829
β
3
and α ∼
0.5483
β
4
;
• In the 4-valued logic α ∼
0.8860
β
1
, α ∼
0.9268
β
2
, α ∼
0.4667
β
3
and α ∼
0.5299
β
4
;
• In the 5-valued logic α ∼
0.8940
β
1
, α ∼
0.9315
β
2
, α ∼
0.4579
β
3
and α ∼
0.6326
β
4
;
• In the 10-valued logic α ∼
0.9085
β
1
, α ∼
0.9399
β
2
, α ∼
0.4418
β
3
and α ∼
0.4991
β
4
.
From observed similarity we selected β
2
as the best
approximation to α. Its quality, as an approximation,
improves when we increase the logics number of truth
values. Similarity increases with the increase in the
number of evaluations.
In this sense, rule R can be used for configuration
classification and configuration approximation. From
an un-representable configuration, α, we can gener-
ate the finite set S(α), with representable networks
similar to α, using rule R. Given a (n + 1)-valued
logic, from that set of formulas we can select as an
approximation to α; the formula having the interpre-
tation more similar to α. This identification of un-
representable configuration, using representable ap-
proximations, is used to transform networks with un-
representable neurons into representable structures.
The stress associated with this transformation char-
acterizes the translation accuracy.
2.4 Neural Network Crystallization
Weights in CNNs assume the values -1 or 1. However,
the usual learning algorithms process NNs weights,
presupposing the continuity of the weights domain.
Naturally, every NN with weighs in [−1,1] can be
seen as an approximation to a CNNs. The process of
identifying a NN with weighs in [−1,1] as a ŁNNs
is called crystallization, and essentially consists in
rounding each neural weight w
i
to the nearest integer
less than or equal to w
i
, denoted by bw
i
c.
In this sense the crystallization process can be
seen as a pruning on the network structure, where
links between neurons with weights near 0 are re-
moved and weights near -1 or 1 are consolidated.
However this process is very crispy. We need a
smooth procedure to crystallize a network, in each
learning iteration, to avoid the drastic reduction in
learning performance. In each iteration we restricted
the NN representation bias, making the network rep-
resentation bias converge to a structure similar to a
CNN. For that, we defined by representation error for
a network N with weights w
1
,...,w
n
, as
∆(N)=
∑
n
i=1
(w
i
−bw
i
c).
(12)
When N is a CNNs we have ∆(N) = 0. Our smooth
crystallization process results from the iterating of
function:
ϒ
n
(w)=sign(w).((cos(1−abs(w)−babs(w)c).
π
2
)
n
+babs(w)c),
IJCCI 2009 - International Joint Conference on Computational Intelligence
10
where sign(w) is the sign of w and abs(w) its absolute
value. Denoting by ϒ
n
(N) the function having by in-
put and output a NN, where the weights on the output
network results of applying ϒ to all the input network
weights and neurons biases. Each interactive appli-
cation of ϒ produce a networks progressively more
similar to a CNNs. Since, for every network N and
n > 0, ∆(N) ≥ ∆(ϒ
n
(N)), we have:
Proposition 7. Given a NNs N with weights in the
interval [0,1]. For every n > 0 the function ϒ
n
(N)
has, by fixed points, a CNNs.
The convergence speed depends on parameter n.
Increasing n speeds up crystallization but reduces the
network’s plasticity to the training data. For our ap-
plications, we selected n = 2 based on the learning ef-
ficiency of a set of test formulas. Greater values for n
imposes stronger restrictions to learning. This proce-
dure induces a quicker convergence to an admissible
configuration of CNNs.
3 LEARNING PROPOSITIONS
We began the study of knowledge extraction using a
CNN by reverse engineering a truth table. By this
we mean that, for a given truth table on a (n + 1)-
valued Łukasiewicz logic, generated using a formula
in the Łukasiewicz logic language, we will try to find
its interpretation in the form of a ŁNN, and from it,
rediscover the original formula.
For that we trained a feed-forward NN using a
truth table. Our methodology trains progressively
more complex networks until a crystallized network
with good performance has been found. Note that
convergence depends on the selected training algo-
rithm.
The methodology is described in algorithm 1 that
is used on the truth table reverse engineering task.
Algorithm 1 : Reverse Engineering algorithm.
1: Given a (n + 1)-valued truth sub-table for a Łukasiewicz logic proposition
2: Define an inicial network complexity
3: Generate an inicial NN
4: Apply (the selected) Backpropagation algorithm using the data set
5: if the generated network have bad performance then
6: If need increase network complexity
7: Try a new network. Go to 3
8: end if
9: Do neural network crystallization using the crisp process.
10: if crystalized network have bad performance then
11: Try a new network. Go to 3
12: end if
13: Refine the crystalized network
Given part of a truth table we try to find a ŁNN
that codifies the data. For this we generated NNs
with a fixed number of hidden layers (our implemen-
tation uses three hidden layers). When the process
detects bad learning performances, it aborts the train-
ing, generating a new network with random heights.
After a fixed number of tries, the network topology is
changed. The number of tries for each topology de-
pends on the number of network inputs. After trying
to configure a set of networks for a given complex-
ity with bad learning performance, the system tries
to apply the selected back-propagation algorithm to a
more complex set of networks. In the following we
presented a short description for the selected learning
algorithm.
If the continuous optimization process converges,
i.e. if the system finds a network codifying the data,
the network is crystallized. When the error associ-
ated to this process increase, the system returns to the
learning phase and tries to configure a new network.
When the process converges and the resulting net-
work can be codified as a crisp ŁNN the system
prunes the network. The goal of this phase is net-
work simplification. For this, we selected the Opti-
mal Brain Surgeon algorithm proposed by G.J. Wolf,
B. Hassibi and D.G. Stork in (Hassibi et al., 1993).
Figure 5 presents an example of the reverse engi-
neering algorithm input data set (a truth table in a 2-
valued logic generated using ’xor’) and the resulting
NN output structure.
Figure 5: Input and Output structures.
3.1 Training
Standard error back-propagation algorithm (EBP) is
a gradient descent algorithm, in which the network
weights are moved along the negative of the gradient
of the performance function. EBP algorithm has been
a significant improvement in NN research, but it has a
weak convergence rate. Many efforts have been made
to speed up the EBP algorithm (Bello, 1992) (Samad,
1990) (Solla et al., 1988) (Miniani and Williams,
1990) (Jacobs, 1988). The Levenderg-Marquardt al-
gorithm (LM) (Hagan and Menhaj, 1999) (Andersen
and Wilamowski, 1995) (Battiti, 1992) (Charalam-
bous, 1992) ensued from the development of EBP
algorithm-dependent methods. It gives a good ex-
change between the speed of the Newton algorithm
and the stability of the steepest descent method (Bat-
titi, 1992).
REVERSE ENGINEERING AND SYMBOLIC KNOWLEDGE EXTRACTION ON AUKASIEWICZ LOGICS USING
NEURAL NETWORKS
11
The basic EBP algorithm adjusts the weights in
the steepest descent direction. This is the direction
in which the performance function is decreasing most
rapidly. In the EBP algorithm, the performance in-
dex F(w) to be minimized is defined as the sum of
squared erros between the target output and the net-
work’s simulated outputs. When training with the
EBP method, an iteration of the algorithm defines the
change of weights and has the form
w
k+1
=w
k
−αG
k
,
(13)
where G
k
is the gradient of F on w
k
, and α is the
learning rate.
Note that the basic step of Newton’s method can
be derived from Taylor formula and is:
w
k+1
=w
k
−H
−1
k
G
k
,
(14)
where H
k
is the Hessian matrix of the performance
index at the current values of the weights.
Since Newton’s method implicitly uses quadratic
assumptions (arising from the neglect of higher-order
terms in a Taylor series), the Hessian matrix dos not
need be evaluated exactly. Rather, an approximation
can be used, such as
H
k
≈J
T
k
J
k
,
(15)
where J
k
is the Jacobian matrix that contains first
derivatives of the network errors with respect to the
weights w
k
. The Jacobian matrix J
k
can be com-
puted through a standard back-propagation technique
(Mehrotra et al., 1997) that is much less complex than
computing the Hessian matrix.
The simple gradient descent and newtonian itera-
tion are complementary in the advantages they pro-
vide. Levenberg proposed an algorithm based on
this observation, whose update rule blends aforemen-
tioned algorithms and is given as
w
k+1
=w
k
−[J
T
k
J
k
+µI]
−1
J
T
k
e
k
, (16)
where J
k
is the Jacobian matrix evaluated at w
k
and µ
is the learning rate. This update rule is used as fol-
lows. If the error goes down following an update, it
implies that our quadratic assumption on the function
is working and we reduce µ (usually by a factor of 10)
to reduce the influence of gradient descent. In this
way, the performance function is always reduced at
each iteration of the algorithm (Hagan et al., 1996).
On the other hand, if the error goes up, we would like
to follow the gradient more and so µ is increased by
the same factor.
The algorithm has the disadvantage that if the
value of µ is large, the approximation to the Hes-
sian matrix is not used at all. We can obtain some
advantage out of the second derivative, even in such
cases, by scaling each component of the gradient ac-
cording to the curvature. This should result in larger
movements along the direction where the gradient is
smaller so the classic ”error valley” problem does not
occur any more. This crucial insight was provided
by Marquardt. He replaced the identity matrix in
the Levenberg update rule with the diagonal of Hes-
sian matrix approximation resulting in the Levenberg-
Marquardt update rule.
w
k+1
=w
k
−[J
T
k
J
k
+µ.diag(J
T
k
J
k
)]
−1
J
T
k
e
k
.
(17)
We changed the Levenberg-Marquardt algorithm
by applying a soft crystallization step after the
Levenberg-Marquardt update rule:
w
k+1
=ϒ
2
(w
k
−[J
T
k
J
k
+µ.diag(J
T
k
J
k
)]
−1
J
T
k
e
k
) (18)
This drastically improves the convergence to a CNN.
In our methodology regularization is made using
three different strategies:
1. using soft crystallization, where knowledge dis-
semination is restricted on the network, informa-
tion is concentrated on some weights;
2. using crisp crystallization where only the heavier
weights survive defines the network topology;
3. pruning the resulting crystallized network.
The last regularization technic avoids redundancies,
in the sense that the same or redundant information
can be codified at different locations. We minimized
this by selecting weights to eliminate. For this task,
we used ”Optimal Brain Surgeon” (OBS) method pro-
posed by B. Hassibi, D. G. Stork and G.J. Stork in
(Hassibi et al., 1993), which uses the criterion of min-
imal increase in training error. It uses information
from all second-order derivatives of the error function
to perform network pruning.
Our method is in no way optimal, it is just a
heuristic, however works extremely well for learning
CNNs.
4 REVERSE ENGINEERING
Given a ŁNN it can be translated in the form of a
string base formula if every neuron is representable.
Proposition 4 defines a tool to translate from the con-
nectionist representation to a symbolic representation.
It is remarkable that, when the truth table sample
used in the learning was generated by a formula, the
Reverse Engineering algorithm converges to a rep-
resentable ŁNN equivalent to the original formula,
when evaluated on the cases used in the truth table
sample.
IJCCI 2009 - International Joint Conference on Computational Intelligence
12
When we generate a truth table in the 4-valued
Łukasiewicz logic using formula
(x
4
⊗x
5
⇒x
6
)⊗(x
1
⊗x
5
⇒x
2
)⊗(x
1
⊗x
2
⇒x
3
)⊗(x
6
⇒x
4
)
it has 4096 cases, the result of applying the algorithm
is the 100% accurate NN:
When we generate a truth table in the 4-valued
Łukasiewicz logic using formula
(x
4
⊗x
5
⇒x
6
)⊗(x
1
⊗x
5
⇒x
2
)⊗(x
1
⊗x
2
⇒x
3
)⊗(x
6
⇒x
4
)
it has 4096 cases, the result of applying the algorithm
is the 100% accurate NN:
0 0 0 −1 0 1
0 0 0 1 1 −1
1 1 −1 0 0 0
−1 1 0 0 −1 0
0
−1
−1
2
¬x
4
⊗ x
6
x
4
⊗ x
5
⊗ ¬x
6
x
1
⊗ x
2
⊗ ¬x
3
¬x
1
⊕ x
2
⊕ ¬x
5
−1 −1 −1 1
0
¬i
1
⊗ ¬i
2
⊗ ¬i
3
⊗ i
4
1
0
j
1
Using local interpretation we may reconstruct the for-
mula:
j
1
= ¬i
1
⊗ ¬i
2
⊗ ¬i
3
⊗ i
4
=
¬(¬x
4
⊗ x
6
) ⊗ ¬(x
4
⊗ x
5
⊗ ¬x
6
) ⊗ ¬(x
1
⊗ x
2
⊗ ¬x
3
) ⊗ (¬x
1
⊕ x
2
⊕ ¬x
5
) =
= (x
4
⊕ ¬x
6
) ⊗ (¬x
4
⊕ ¬x
5
⊕ x
6
) ⊗ (¬x
1
⊕ ¬x
2
⊕ x
3
) ⊗ (¬x
1
⊕ x
2
⊕ ¬x
5
) =
= (x
6
⇒ x
4
) ⊗ (x
4
⊗ x
5
⇒ x
6
) ⊗ (x
1
⊗ x
2
⇒ x
3
) ⊗ (x
1
⊗ x
5
⇒ x2)
Note, however, that the restriction imposed in our
implementation of three hidden layers wherein the
last hidden layer has only one neuron, restrict the
complexity of reconstructed formula. For instance,
in order for
((x
4
⊗x
5
⇒x
6
)⊕(x
1
⊗x
5
⇒x
2
))⊗(x
1
⊗x
2
⇒x
3
)⊗(x
6
⇒x
4
)
to be codified in a three hidden layer network the last
layer needs two neurons one to codify the disjunction
and the other to codify the conjunctions. When the al-
gorithm was applied to the truth table generated in the
4-valued Łukasiewicz logic by using a stopping crite-
rion a mean square error less than 0.0007 it produced
the representable network:
0 0 0 1 0 −1
1 −1 0 1 1 −1
1 1 −1 0 0 0
1
−2
−1
x
4
⊕ ¬x
6
x
1
⊗ ¬x
2
⊗ x
4
⊗ x
5
⊗ ¬x
6
x
1
⊗ x
2
⊗ ¬x
3
1 −1 −1
0
i
1
⊗ ¬i
2
⊗ ¬i
3
1
0
j
1
By this we may conclude what original formula can
be approximate, or is λ-similar with λ = 0.998 to:
j
1
= i
1
⊗ ¬i
2
⊗ ¬i
3
= (x
4
⊕ ¬x
6
) ⊗ ¬(x
1
⊗ ¬x
2
⊗ x
4
⊗ x
5
⊗ ¬x
6
) ⊗ ¬(x
1
⊗ x
2
⊗ ¬x
3
) =
= (x
4
⊕ ¬x
6
) ⊗ (¬x
1
⊕ x
2
⊕ ¬x
4
⊕ ¬x
5
⊕ x
6
) ⊗ (¬x
1
⊕ ¬x
2
⊕ x
3
) =
= (x
6
⇒ x
4
) ⊗ ((x
1
⊗ x
4
⊗ x
5
) ⇒ (x
2
⊕ x
6
)) ⊗ (x
1
⊗ x
2
⇒ x
3
)
Note that j
1
is 0.998-similar to the original formula in
the 4-valued Łukasiewicz logic but it is equivalent to
the original in the 2-valued Łukasiewicz logic, i.e. in
Boolean logic.
The fixed number of layers also imposes restric-
tions to reconstruction of formula. A truth table gen-
erated by:
(((i
1
⊗i
2
)⊕(i
2
⊗i
3
))⊗((i
3
⊗i
4
)⊕(i
4
⊗i
5
)))⊕(i
5
⊗i
6
)
requires at least 4 hidden layers, to be reconstructed;
this is the number of levels required by the associated
parsing tree.
Table 2 presents the mean CPU times need to find
a configuration with a mean square error of less than
0.002. The mean time is computed using 6 trials on
formula mean stdev
i
1
⊗ i
3
⇒ i
6
7.68 6.27
i
4
⇒ i
6
⊗ i
6
⇒ i
2
25.53 11.14
((i
1
⇒ i
4
) ⊕ (i
6
⇒ i
2
)) ⊗ (i
6
⇒ i
1
) 43.27 14.25
(i
4
⊗ i
5
⇒ i
6
) ⊗ (i
1
⊗ i
5
⇒ i
2
) 51.67 483.85
((i
4
⊗ i
5
⇒ i
6
) ⊕ (i
1
⊗ i
5
⇒ i
2
)) ⊗ (i
1
⊗ i
3
⇒ i
2
) 268.31 190.99
((i
4
⊗ i
5
⇒ i
6
) ⊕ (i
1
⊗ i
5
⇒ i
2
)) ⊗ (i
1
⊗ i
3
⇒ i
2
) ⊗ (i
6
⇒ i
4
) 410.47 235.52
Table 2: Reverse engineering test formulas.
a 5-valued truth Łukasiewicz logic for each formula.
We implemented the algorithm using the MatLab NN
package and executed it in an AMD Athlon 64 X2
Dual-Core Processor TK-53 at 1.70 GHz on a Win-
dows Vista system with 959MB of memory. In table
2 the last two formula was approximated, since we re-
stricted the structure for NNs to three hidden layers,
for others each extraction process made equivalent re-
constructions.
5 REAL DATA
Extracting symbolic rules from a real data set can
be a very different task than reverse-engineering the
rule used on the generation of an artificial data set, in
sense that, in the reverse engineering task, we know
the existence of a perfect description. In particular,
we know the appropriate logic language to describe
it and we have no noise. The process of symbolic
extraction from the real data set is made by establish-
ing a stopping criterion and having a language bias
defined by the extraction methodology. The expres-
sive power of this language characterizes the learning
algorithm plasticity. Very expressive languages pro-
duce good fitness to data, but usually bad generaliza-
tion, and the extracted sentences usually are difficult
to understand by human experts.
The described extraction process, when applied to
real data, expresses the information using CNNs. This
naturally means that the process searches for simple
and understandable models for the data, able to be
codify directly or approximated using Łukasiewicz
logic language. The process gives preference to the
simplest models and subject them to a strong pruning
criteria. With this strategy we avoid overfetting and
the problems associated with the algorithm complex-
ity.
The process, however, can be prohibitive to train
complex models having a great number of links. To
avoid this, the rule extraction must be preceded by a
phase of attribute selection.
Using local interpretation we may reconstruct the for-
mula:
j
1
= ¬i
1
⊗ ¬i
2
⊗ ¬i
3
⊗ i
4
=
¬(¬x
4
⊗ x
6
) ⊗ ¬(x
4
⊗ x
5
⊗ ¬x
6
) ⊗ ¬(x
1
⊗ x
2
⊗ ¬x
3
) ⊗ (¬x
1
⊕ x
2
⊕ ¬x
5
) =
= (x
4
⊕ ¬x
6
) ⊗ (¬x
4
⊕ ¬x
5
⊕ x
6
) ⊗ (¬x
1
⊕ ¬x
2
⊕ x
3
) ⊗ (¬x
1
⊕ x
2
⊕ ¬x
5
) =
= (x
6
⇒ x
4
) ⊗ (x
4
⊗ x
5
⇒ x
6
) ⊗ (x
1
⊗ x
2
⇒ x
3
) ⊗ (x
1
⊗ x
5
⇒ x2)
Note, however, that the restriction imposed in our
implementation of three hidden layers wherein the
last hidden layer has only one neuron, restrict the
complexity of reconstructed formula. For instance,
in order for
((x
4
⊗x
5
⇒x
6
)⊕(x
1
⊗x
5
⇒x
2
))⊗(x
1
⊗x
2
⇒x
3
)⊗(x
6
⇒x
4
)
to be codified in a three hidden layer network the last
layer needs two neurons one to codify the disjunction
and the other to codify the conjunctions. When the al-
gorithm was applied to the truth table generated in the
4-valued Łukasiewicz logic by using a stopping crite-
rion a mean square error less than 0.0007 it produced
the representable network:
When we generate a truth table in the 4-valued
Łukasiewicz logic using formula
(x
4
⊗x
5
⇒x
6
)⊗(x
1
⊗x
5
⇒x
2
)⊗(x
1
⊗x
2
⇒x
3
)⊗(x
6
⇒x
4
)
it has 4096 cases, the result of applying the algorithm
is the 100% accurate NN:
0 0 0 −1 0 1
0 0 0 1 1 −1
1 1 −1 0 0 0
−1 1 0 0 −1 0
0
−1
−1
2
¬x
4
⊗ x
6
x
4
⊗ x
5
⊗ ¬x
6
x
1
⊗ x
2
⊗ ¬x
3
¬x
1
⊕ x
2
⊕ ¬x
5
−1 −1 −1 1
0
¬i
1
⊗ ¬i
2
⊗ ¬i
3
⊗ i
4
1
0
j
1
Using local interpretation we may reconstruct the for-
mula:
j
1
= ¬i
1
⊗ ¬i
2
⊗ ¬i
3
⊗ i
4
=
¬(¬x
4
⊗ x
6
) ⊗ ¬(x
4
⊗ x
5
⊗ ¬x
6
) ⊗ ¬(x
1
⊗ x
2
⊗ ¬x
3
) ⊗ (¬x
1
⊕ x
2
⊕ ¬x
5
) =
= (x
4
⊕ ¬x
6
) ⊗ (¬x
4
⊕ ¬x
5
⊕ x
6
) ⊗ (¬x
1
⊕ ¬x
2
⊕ x
3
) ⊗ (¬x
1
⊕ x
2
⊕ ¬x
5
) =
= (x
6
⇒ x
4
) ⊗ (x
4
⊗ x
5
⇒ x
6
) ⊗ (x
1
⊗ x
2
⇒ x
3
) ⊗ (x
1
⊗ x
5
⇒ x2)
Note, however, that the restriction imposed in our
implementation of three hidden layers wherein the
last hidden layer has only one neuron, restrict the
complexity of reconstructed formula. For instance,
in order for
((x
4
⊗x
5
⇒x
6
)⊕(x
1
⊗x
5
⇒x
2
))⊗(x
1
⊗x
2
⇒x
3
)⊗(x
6
⇒x
4
)
to be codified in a three hidden layer network the last
layer needs two neurons one to codify the disjunction
and the other to codify the conjunctions. When the al-
gorithm was applied to the truth table generated in the
4-valued Łukasiewicz logic by using a stopping crite-
rion a mean square error less than 0.0007 it produced
the representable network:
0 0 0 1 0 −1
1 −1 0 1 1 −1
1 1 −1 0 0 0
1
−2
−1
x
4
⊕ ¬x
6
x
1
⊗ ¬x
2
⊗ x
4
⊗ x
5
⊗ ¬x
6
x
1
⊗ x
2
⊗ ¬x
3
1 −1 −1
0
i
1
⊗ ¬i
2
⊗ ¬i
3
1
0
j
1
By this we may conclude what original formula can
be approximate, or is λ-similar with λ = 0.998 to:
j
1
= i
1
⊗ ¬i
2
⊗ ¬i
3
= (x
4
⊕ ¬x
6
) ⊗ ¬(x
1
⊗ ¬x
2
⊗ x
4
⊗ x
5
⊗ ¬x
6
) ⊗ ¬(x
1
⊗ x
2
⊗ ¬x
3
) =
= (x
4
⊕ ¬x
6
) ⊗ (¬x
1
⊕ x
2
⊕ ¬x
4
⊕ ¬x
5
⊕ x
6
) ⊗ (¬x
1
⊕ ¬x
2
⊕ x
3
) =
= (x
6
⇒ x
4
) ⊗ ((x
1
⊗ x
4
⊗ x
5
) ⇒ (x
2
⊕ x
6
)) ⊗ (x
1
⊗ x
2
⇒ x
3
)
Note that j
1
is 0.998-similar to the original formula in
the 4-valued Łukasiewicz logic but it is equivalent to
the original in the 2-valued Łukasiewicz logic, i.e. in
Boolean logic.
The fixed number of layers also imposes restric-
tions to reconstruction of formula. A truth table gen-
erated by:
(((i
1
⊗i
2
)⊕(i
2
⊗i
3
))⊗((i
3
⊗i
4
)⊕(i
4
⊗i
5
)))⊕(i
5
⊗i
6
)
requires at least 4 hidden layers, to be reconstructed;
this is the number of levels required by the associated
parsing tree.
Table 2 presents the mean CPU times need to find
a configuration with a mean square error of less than
0.002. The mean time is computed using 6 trials on
formula mean stdev
i
1
⊗ i
3
⇒ i
6
7.68 6.27
i
4
⇒ i
6
⊗ i
6
⇒ i
2
25.53 11.14
((i
1
⇒ i
4
) ⊕ (i
6
⇒ i
2
)) ⊗ (i
6
⇒ i
1
) 43.27 14.25
(i
4
⊗ i
5
⇒ i
6
) ⊗ (i
1
⊗ i
5
⇒ i
2
) 51.67 483.85
((i
4
⊗ i
5
⇒ i
6
) ⊕ (i
1
⊗ i
5
⇒ i
2
)) ⊗ (i
1
⊗ i
3
⇒ i
2
) 268.31 190.99
((i
4
⊗ i
5
⇒ i
6
) ⊕ (i
1
⊗ i
5
⇒ i
2
)) ⊗ (i
1
⊗ i
3
⇒ i
2
) ⊗ (i
6
⇒ i
4
) 410.47 235.52
Table 2: Reverse engineering test formulas.
a 5-valued truth Łukasiewicz logic for each formula.
We implemented the algorithm using the MatLab NN
package and executed it in an AMD Athlon 64 X2
Dual-Core Processor TK-53 at 1.70 GHz on a Win-
dows Vista system with 959MB of memory. In table
2 the last two formula was approximated, since we re-
stricted the structure for NNs to three hidden layers,
for others each extraction process made equivalent re-
constructions.
5 REAL DATA
Extracting symbolic rules from a real data set can
be a very different task than reverse-engineering the
rule used on the generation of an artificial data set, in
sense that, in the reverse engineering task, we know
the existence of a perfect description. In particular,
we know the appropriate logic language to describe
it and we have no noise. The process of symbolic
extraction from the real data set is made by establish-
ing a stopping criterion and having a language bias
defined by the extraction methodology. The expres-
sive power of this language characterizes the learning
algorithm plasticity. Very expressive languages pro-
duce good fitness to data, but usually bad generaliza-
tion, and the extracted sentences usually are difficult
to understand by human experts.
The described extraction process, when applied to
real data, expresses the information using CNNs. This
naturally means that the process searches for simple
and understandable models for the data, able to be
codify directly or approximated using Łukasiewicz
logic language. The process gives preference to the
simplest models and subject them to a strong pruning
criteria. With this strategy we avoid overfetting and
the problems associated with the algorithm complex-
ity.
The process, however, can be prohibitive to train
complex models having a great number of links. To
avoid this, the rule extraction must be preceded by a
phase of attribute selection.
By this we may conclude what original formula
can be approximate, or is λ-similar with λ = 0.998 to:
j
1
= i
1
⊗ ¬i
2
⊗ ¬i
3
= (x
4
⊕ ¬x
6
) ⊗ ¬(x
1
⊗ ¬x
2
⊗ x
4
⊗ x
5
⊗ ¬x
6
) ⊗ ¬(x
1
⊗ x
2
⊗ ¬x
3
) =
= (x
4
⊕ ¬x
6
) ⊗ (¬x
1
⊕ x
2
⊕ ¬x
4
⊕ ¬x
5
⊕ x
6
) ⊗ (¬x
1
⊕ ¬x
2
⊕ x
3
) =
= (x
6
⇒ x
4
) ⊗ ((x
1
⊗ x
4
⊗ x
5
) ⇒ (x
2
⊕ x
6
)) ⊗ (x
1
⊗ x
2
⇒ x
3
)
Note that j
1
is 0.998-similar to the original formula in
the 4-valued Łukasiewicz logic but it is equivalent to
the original in the 2-valued Łukasiewicz logic, i.e. in
Boolean logic.
The fixed number of layers also imposes restric-
tions to reconstruction of formula. A truth table gen-
erated by:
(((i
1
⊗i
2
)⊕(i
2
⊗i
3
))⊗((i
3
⊗i
4
)⊕(i
4
⊗i
5
)))⊕(i
5
⊗i
6
)
requires at least 4 hidden layers, to be reconstructed;
this is the number of levels required by the associated
parsing tree.
Table 2 presents the mean CPU times need to find
a configuration with a mean square error of less than
0.002. The mean time is computed using 6 trials on
a 5-valued truth Łukasiewicz logic for each formula.
We implemented the algorithm using the MatLab NN
Table 2: Reverse engineering test formulas.
When we generate a truth table in the 4-valued
Łukasiewicz logic using formula
(x
4
⊗x
5
⇒x
6
)⊗(x
1
⊗x
5
⇒x
2
)⊗(x
1
⊗x
2
⇒x
3
)⊗(x
6
⇒x
4
)
it has 4096 cases, the result of applying the algorithm
is the 100% accurate NN:
0 0 0 −1 0 1
0 0 0 1 1 −1
1 1 −1 0 0 0
−1 1 0 0 −1 0
0
−1
−1
2
¬x
4
⊗ x
6
x
4
⊗ x
5
⊗ ¬x
6
x
1
⊗ x
2
⊗ ¬x
3
¬x
1
⊕ x
2
⊕ ¬x
5
−1 −1 −1 1
0
¬i
1
⊗ ¬i
2
⊗ ¬i
3
⊗ i
4
1
0
j
1
Using local interpretation we may reconstruct the for-
mula:
j
1
= ¬i
1
⊗ ¬i
2
⊗ ¬i
3
⊗ i
4
=
¬(¬x
4
⊗ x
6
) ⊗ ¬(x
4
⊗ x
5
⊗ ¬x
6
) ⊗ ¬(x
1
⊗ x
2
⊗ ¬x
3
) ⊗ (¬x
1
⊕ x
2
⊕ ¬x
5
) =
= (x
4
⊕ ¬x
6
) ⊗ (¬x
4
⊕ ¬x
5
⊕ x
6
) ⊗ (¬x
1
⊕ ¬x
2
⊕ x
3
) ⊗ (¬x
1
⊕ x
2
⊕ ¬x
5
) =
= (x
6
⇒ x
4
) ⊗ (x
4
⊗ x
5
⇒ x
6
) ⊗ (x
1
⊗ x
2
⇒ x
3
) ⊗ (x
1
⊗ x
5
⇒ x2)
Note, however, that the restriction imposed in our
implementation of three hidden layers wherein the
last hidden layer has only one neuron, restrict the
complexity of reconstructed formula. For instance,
in order for
((x
4
⊗x
5
⇒x
6
)⊕(x
1
⊗x
5
⇒x
2
))⊗(x
1
⊗x
2
⇒x
3
)⊗(x
6
⇒x
4
)
to be codified in a three hidden layer network the last
layer needs two neurons one to codify the disjunction
and the other to codify the conjunctions. When the al-
gorithm was applied to the truth table generated in the
4-valued Łukasiewicz logic by using a stopping crite-
rion a mean square error less than 0.0007 it produced
the representable network:
0 0 0 1 0 −1
1 −1 0 1 1 −1
1 1 −1 0 0 0
1
−2
−1
x
4
⊕ ¬x
6
x
1
⊗ ¬x
2
⊗ x
4
⊗ x
5
⊗ ¬x
6
x
1
⊗ x
2
⊗ ¬x
3
1 −1 −1
0
i
1
⊗ ¬i
2
⊗ ¬i
3
1
0
j
1
By this we may conclude what original formula can
be approximate, or is λ-similar with λ = 0.998 to:
j
1
= i
1
⊗ ¬i
2
⊗ ¬i
3
= (x
4
⊕ ¬x
6
) ⊗ ¬(x
1
⊗ ¬x
2
⊗ x
4
⊗ x
5
⊗ ¬x
6
) ⊗ ¬(x
1
⊗ x
2
⊗ ¬x
3
) =
= (x
4
⊕ ¬x
6
) ⊗ (¬x
1
⊕ x
2
⊕ ¬x
4
⊕ ¬x
5
⊕ x
6
) ⊗ (¬x
1
⊕ ¬x
2
⊕ x
3
) =
= (x
6
⇒ x
4
) ⊗ ((x
1
⊗ x
4
⊗ x
5
) ⇒ (x
2
⊕ x
6
)) ⊗ (x
1
⊗ x
2
⇒ x
3
)
Note that j
1
is 0.998-similar to the original formula in
the 4-valued Łukasiewicz logic but it is equivalent to
the original in the 2-valued Łukasiewicz logic, i.e. in
Boolean logic.
The fixed number of layers also imposes restric-
tions to reconstruction of formula. A truth table gen-
erated by:
(((i
1
⊗i
2
)⊕(i
2
⊗i
3
))⊗((i
3
⊗i
4
)⊕(i
4
⊗i
5
)))⊕(i
5
⊗i
6
)
requires at least 4 hidden layers, to be reconstructed;
this is the number of levels required by the associated
parsing tree.
Table 2 presents the mean CPU times need to find
a configuration with a mean square error of less than
0.002. The mean time is computed using 6 trials on
formula mean stdev
i
1
⊗ i
3
⇒ i
6
7.68 6.27
i
4
⇒ i
6
⊗ i
6
⇒ i
2
25.53 11.14
((i
1
⇒ i
4
) ⊕ (i
6
⇒ i
2
)) ⊗ (i
6
⇒ i
1
) 43.27 14.25
(i
4
⊗ i
5
⇒ i
6
) ⊗ (i
1
⊗ i
5
⇒ i
2
) 51.67 483.85
((i
4
⊗ i
5
⇒ i
6
) ⊕ (i
1
⊗ i
5
⇒ i
2
)) ⊗ (i
1
⊗ i
3
⇒ i
2
) 268.31 190.99
((i
4
⊗ i
5
⇒ i
6
) ⊕ (i
1
⊗ i
5
⇒ i
2
)) ⊗ (i
1
⊗ i
3
⇒ i
2
) ⊗ (i
6
⇒ i
4
) 410.47 235.52
Table 2: Reverse engineering test formulas.
a 5-valued truth Łukasiewicz logic for each formula.
We implemented the algorithm using the MatLab NN
package and executed it in an AMD Athlon 64 X2
Dual-Core Processor TK-53 at 1.70 GHz on a Win-
dows Vista system with 959MB of memory. In table
2 the last two formula was approximated, since we re-
stricted the structure for NNs to three hidden layers,
for others each extraction process made equivalent re-
constructions.
5 REAL DATA
Extracting symbolic rules from a real data set can
be a very different task than reverse-engineering the
rule used on the generation of an artificial data set, in
sense that, in the reverse engineering task, we know
the existence of a perfect description. In particular,
we know the appropriate logic language to describe
it and we have no noise. The process of symbolic
extraction from the real data set is made by establish-
ing a stopping criterion and having a language bias
defined by the extraction methodology. The expres-
sive power of this language characterizes the learning
algorithm plasticity. Very expressive languages pro-
duce good fitness to data, but usually bad generaliza-
tion, and the extracted sentences usually are difficult
to understand by human experts.
The described extraction process, when applied to
real data, expresses the information using CNNs. This
naturally means that the process searches for simple
and understandable models for the data, able to be
codify directly or approximated using Łukasiewicz
logic language. The process gives preference to the
simplest models and subject them to a strong pruning
criteria. With this strategy we avoid overfetting and
the problems associated with the algorithm complex-
ity.
The process, however, can be prohibitive to train
complex models having a great number of links. To
avoid this, the rule extraction must be preceded by a
phase of attribute selection.
package and executed it in an AMD Athlon 64 X2
Dual-Core Processor TK-53 at 1.70 GHz on a Win-
dows Vista system with 959MB of memory.
In table 2 the last two formula was approximated,
since we restricted the structure for NNs to three hid-
den layers, for others each extraction process made
equivalent reconstructions.
5 REAL DATA
Extracting symbolic rules from a real data set can be
a very different task than reverse-engineering the rule
used on the generation of an artificial data set, in sense
that, in the reverse engineering task, we know the
existence of a perfect description. In particular, we
know the appropriate logic language to describe it and
we have no noise. The process of symbolic extrac-
tion from the real data set is made by establishing a
stopping criterion and having a language bias defined
by the extraction methodology. The expressive power
of this language characterizes the learning algorithm
plasticity. Very expressive languages produce good
fitness to data, but usually bad generalization, and the
extracted sentences usually are difficult to understand
by human experts.
The described extraction process, when applied to
real data, expresses the information using CNNs. This
naturally means that the process searches for simple
and understandable models for the data, able to be
codify directly or approximated using Łukasiewicz
logic language. The process gives preference to the
simplest models and subject them to a strong pruning
criteria. With this strategy we avoid overfetting and
the problems associated with the algorithm complex-
ity.
The process, however, can be prohibitive to train
complex models having a great number of links. To
avoid this, the rule extraction must be preceded by a
phase of attribute selection.
5.1 Mushrooms
Mushroom is a data set available in the UCI Machine
Learning Repository. This data set includes descrip-
tions of hypothetical samples corresponding to 23
REVERSE ENGINEERING AND SYMBOLIC KNOWLEDGE EXTRACTION ON AUKASIEWICZ LOGICS USING
NEURAL NETWORKS
13
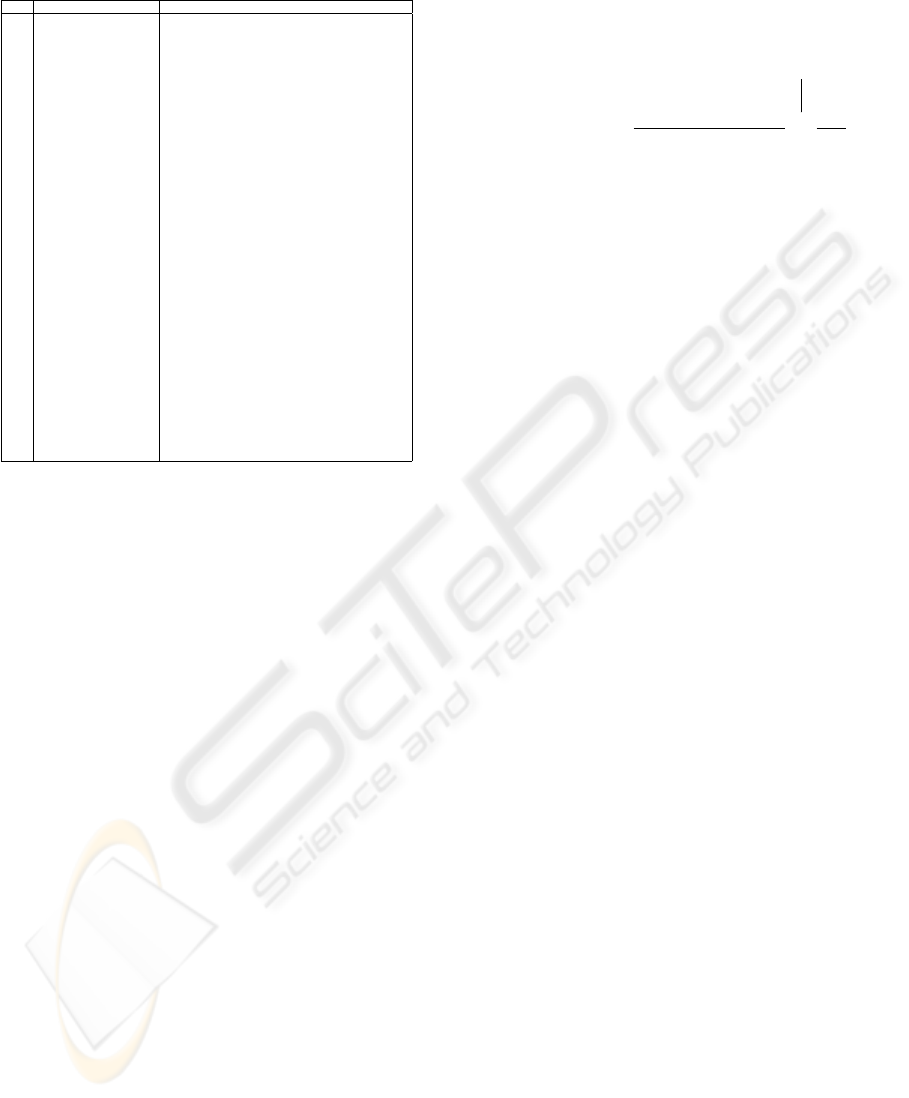
Table 3: Mushroom data set attribute Information.
N. Attribute Values
0 classes edible=e, poisonous=p
1 cap.shape bell=b,conical=c,convex=x,flat=f,knobbed=k,
sunken=s
2 cap.surface fibrous=f,grooves=g,scaly=y,smooth=s
3 cap.color brown=n,buff=b,cinnamon=c,gray=g,green=r,
pink=p,purple=u,red=e,white=w,yellow=y
4 bruises? bruises=t,no=f
5 odor almond=a,anise=l,creosote=c,fishy=y,foul=f,
musty=m,none=n,pungent=p,spicy=s
6 gill.attachment attached=a,descending=d,free=f,notched=n
7 gill.spacing close=c,crowded=w,distant=d
8 gill.size broad=b,narrow=n
9 gill.color black=k,brown=n,buff=b,chocolate=h,gray=g,
green=r,orange=o,pink=p,purple=u,red=e,white=w,
yellow=y
10 stalk.shape enlarging=e,tapering=t
11 stalk.root bulbous=b,club=c,cup=u,equal=e,rhizomorphs=z,
rooted=r,missing=?
12 stalk.surface.above.ring ibrous=f,scaly=y,silky=k,smooth=s
13 stalk.surface.below.ring ibrous=f,scaly=y,silky=k,smooth=s
14 stalk.color.above.ring brown=n,buff=b,cinnamon=c,gray=g,orange=o,
pink=p,red=e,white=w,yellow=y
15 stalk.color.below.ring brown=n,buff=b,cinnamon=c,gray=g,orange=o,
pink=p,red=e,white=w,yellow=y
16 veil.type partial=p,universal=u
17 veil.color brown=n,orange=o,white=w,yellow=y
18 ring.number none=n,one=o,two=t
19 ring.type cobwebby=c,evanescent=e,flaring=f,large=l,none=n,
pendant=p,sheathing=s,zone=z
20 spore.print.color black=k,brown=n,buff=b,chocolate=h,green=r,
orange=o,purple=u,white=w,yellow=y
21 population abundant=a,clustered=c,numerous=n,scattered=s,
several=v,solitary=y
22 habitat grasses=g,leaves=l,meadows=m,paths=p,urban=u,
waste=w,woods=d
Table 3: Mushroom data set attribute Information.
5.1 Mushrooms
Mushroom is a data set available in the UCI Machine
Learning Repository. This data set includes descrip-
tions of hypothetical samples corresponding to 23
species of gilled mushrooms in the Agaricus and Le-
piota Family. Each species is identified as definitely
edible, definitely poisonous, or of unknown edibility
and not recommended. This latter class was combined
with the poisonous one. The Guide clearly states that
there is no simple rule for determining the edibility of
a mushroom. However, we will try to find one using
the data set as a truth table.
The data set has 8124 instances defined using 22
nominally valued attributes presented in the table be-
low. It has missing attribute values, 2480, all for at-
tribute #11. 4208 instances (51.8%) are classified as
edible and 3916 (48.2%) are classified as poisonous.
An example of a known rule for edible mush-
rooms is:
odor=(almond.OR.anise.OR.none).AND.spore-print-color=NOT.green
gives 48 errors, or 99.41% accuracy on the whole
dataset
We used an unsupervised filter that converted all
nominal attributes into binary numeric attributes. An
attribute with k values was transformed into k binary
attributes. This produced a data set containing 111
binary attributes.
After the binarization we used the described
method to select relevant attributes for mushroom
classification by fixing a weak stoping criterion. As
a result, the method produced a model, with 100%
accuracy, depending on 23 binary attributes defined
by values of:
odor,gill.size,stalk.surface.above.ring, ring.type, spore.print.color.
We used the values assumed by these attributes to pro-
duce a new data set. After 3 tries we selected the
model less complex:
A1 : bruises? = t
1
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
A2 : odor ∈ {a, l, n}
1
W
W
W
W
W
W
W
W
W
W
W
W
W
W
W
W
1
A3 : stalk.sur f ace.above.ring = k
−1
[
[
[
[
[
[
[
[
[
[
[
[
[
A4 : ring.ty pe = e
−1
76540123
ϕ
A5 : spore.print.color = r
−1
c
c
c
c
c
c
c
c
c
c
c
c
c
c
A6 : population = c
−1
g
g
g
g
g
g
g
g
g
g
g
g
g
g
g
g
g
A7 : habitat ∈ {g, m,u,d, p, l}
−1
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
A8 : habitat = w
1
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
This model has an accuracy of 100%. From it, and
since attribute values in A2 and A3, as well as the val-
ues in A7 and A8 are auto-exclusive, we used proposi-
tions A1, A2, A3, A4, A5, A6 and A7 to define a new
data set. This new data set was enriched with new
negative cases by introducing, for each original case,
a new one where the truth value of each attribute was
multiplied by 0.5. For instance, the ”eatable” mush-
room case:
(A1=0, A2=1, A3=0, A4=0, A5=0, A6=1, A7=0)
was used on the definition of a new ”poison” case
(A1=0, A2=0.5, A3=0, A4=0, A5=0, A6=0.5, A7=0)
This resulted in a convergence speedup and reduced
the occurrence of un-representable configurations.
When we applied our ”reverse engineering” algo-
rithm to the enriched data set, having as stopping cri-
terion the mean square error (mse) less than 0.003, the
method produced the model:
0 1 0 0 −1 0 1
0 1 0 1 0 0 −1
−1
−1
A2 ⊗ ¬A5 ⊗A7
A2 ⊗ A4 ⊗¬A7
1 1
0
i
1
⊕ i
2
This model codifies the proposition
(A2 ⊗ ¬A5 ⊗A7)⊕ (A2 ⊗ A4⊗ ¬A7)
and misses the classification of 48 cases. It has
99.41% accuracy and can be interpreted as the rule
for eatable mushrooms given by: ”a mushroom is
eatable if its odor=almond.OR.anise.OR.none and
spore.print.color=black.AND.habitat=NOT.waste or
ring.type=evanescent.AND.habitat=NOT.waste.”
More precise model can be produced, by restrict-
ing the stopping criteria. However, this in general,
produces more complex propositions and is more dif-
ficult to understand. For instance with a stopping cri-
terion mse < 0.002 the systems generated the below
species of gilled mushrooms in the Agaricus and Le-
piota Family. Each species is identified as definitely
edible, definitely poisonous, or of unknown edibility
and not recommended. This latter class was combined
with the poisonous one. The Guide clearly states that
there is no simple rule for determining the edibility of
a mushroom. However, we will try to find one using
the data set as a truth table.
The data set has 8124 instances defined using 22
nominally valued attributes presented in the table be-
low. It has missing attribute values, 2480, all for at-
tribute #11. 4208 instances (51.8%) are classified as
edible and 3916 (48.2%) are classified as poisonous.
An example of a known rule for edible mush-
rooms is:
odor=(almond.OR.anise.OR.none).AND.spore-print-color=NOT.green
gives 48 errors, or 99.41% accuracy on the whole
dataset
We used an unsupervised filter that converted all
nominal attributes into binary numeric attributes. An
attribute with k values was transformed into k binary
attributes. This produced a data set containing 111
binary attributes.
After the binarization we used the described
method to select relevant attributes for mushroom
classification by fixing a weak stoping criterion. As
a result, the method produced a model, with 100%
accuracy, depending on 23 binary attributes defined
by values of:
odor,gill.size,stalk.surface.above.ring, ring.type, spore.print.color.
We used the values assumed by these attributes to
produce a new data set. After 3 tries we selected the
model less complex:
A1 : bruises? = t
1
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
A2 : odor ∈ {a, l, n}
1
W
W
W
W
W
W
W
W
W
W
W
W
W
W
W
W
1
A3 : stalk.sur face.above.ring = k
−1
[
[
[
[
[
[
[
[
[
[
[
[
[
A4 : ring.type = e
−1
76540123
ϕ
A5 : spore.print.color = r
−1
c
c
c
c
c
c
c
c
c
c
c
c
c
c
A6 : population = c
−1
g
g
g
g
g
g
g
g
g
g
g
g
g
g
g
g
g
A7 : habitat ∈ {g, m, u, d, p, l}
−1
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
A8 : habitat = w
1
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
This model has an accuracy of 100%. From it, and
since attribute values in A2 and A3, as well as the val-
ues in A7 and A8 are auto-exclusive, we used proposi-
tions A1, A2, A3, A4, A5, A6 and A7 to define a new
data set. This new data set was enriched with new
negative cases by introducing, for each original case,
a new one where the truth value of each attribute was
multiplied by 0.5. For instance, the ”eatable” mush-
room case:
(A1=0, A2=1, A3=0, A4=0, A5=0, A6=1, A7=0)
was used on the definition of a new ”poison” case
(A1=0, A2=0.5, A3=0, A4=0, A5=0, A6=0.5, A7=0)
This resulted in a convergence speedup and reduced
the occurrence of un-representable configurations.
When we applied our ”reverse engineering” algo-
rithm to the enriched data set, having as stopping cri-
terion the mean square error (mse) less than 0.003, the
method produced the model:
0 1 0 0 −1 0 1
0 1 0 1 0 0 −1
−1
−1
A2 ⊗ ¬A5 ⊗ A7
A2 ⊗ A4 ⊗ ¬A7
1 1
0
i
1
⊕ i
2
This model codifies the proposition
(A2 ⊗ ¬A5 ⊗ A7) ⊕ (A2 ⊗ A4 ⊗ ¬A7)
and misses the classification of 48 cases. It has
99.41% accuracy and can be interpreted as the rule
for eatable mushrooms given by: ”a mushroom is
eatable if its odor=almond.OR.anise.OR.none and
spore.print.color=black.AND.habitat=NOT.waste or
ring.type=evanescent.AND.habitat=NOT.waste.”
More precise model can be produced, by restrict-
ing the stopping criteria. However, this in general,
produces more complex propositions and is more dif-
ficult to understand. For instance with a stopping cri-
terion mse < 0.002 the systems generated the below
model. It misses 32 cases, has an accuracy of 99.2%,
and it is easy to convert in a proposition.
model. It misses 32 cases, has an accuracy of 99.2%,
and it is easy to convert in a proposition.
0 0 0 −1 0 0 1
1 1 0 −1 0 0 0
0 0 0 0 0 0 1
0 1 0 0 −1 −1 1
1
−1
0
−1
¬A4 ⊕ A7
A1 ⊗ A2 ⊗¬A4
A7
A2 ⊗ ¬A5 ⊗¬A6 ⊗ A7
−1 0 1 0
1 −1 0 −1
1
0
¬i
1
⊕ i
3
i
1
⊗ ¬i
2
⊗ ¬i
4
1 −1
0
j
1
⊗ ¬ j
2
This NN can be used to interprete formula:
j
1
⊗ ¬ j
2
= (¬i
1
⊕ i
3
) ⊗ ¬(i
1
⊗ ¬i
2
⊗ ¬i
4
) = (¬(¬A4 ⊕A7) ⊕ A7) ⊗¬((¬A4 ⊕ A7) ⊗
¬(A1 ⊗ A2 ⊗¬A4) ⊗ ¬(A2 ⊗¬A5 ⊗ ¬A6 ⊗A7))) =
= ((A4 ⊗¬A7) ⊕ A7) ⊗((A4 ⊗ ¬A7) ⊕(A1 ⊗ A2 ⊗¬A4) ⊕ (A2 ⊗¬A5 ⊗ ¬A6 ⊗A7)))
Some times the algorithm converged to un-
representable configurations like the one presented
below, with 100% accuracy. The frequency of this
type of configurations increases with the increase of
required accuracy.
−1 1 −1 1 0 −1 0
0 0 0 1 1 0 −1
1 1 0 0 0 0 −1
0
1
0
i
1
un-representable
A4 ⊗ A5 ⊗¬A7
i
3
un-representable
1 −1 1
0
j
1
un-representable
Using rule R and selecting the best approximation in
data set to each un-representable formula, evaluated
in the data set, we have:
1. i
1
∼
0.9297
((¬A1 ⊗ A4) ⊕A2) ⊗ ¬A3 ⊗¬A6
2. i
3
∼
1.0
(A1 ⊕ ¬A7) ⊗A2
3. j
1
∼
0.9951
(i
1
⊗ ¬i
2
) ⊕ i
3
The extracted formula
α = (((((¬A1 ⊗ A4) ⊕A2) ⊗ ¬A3 ⊗¬A6) ⊗ ¬(A4⊗ A5 ⊗ ¬A7))⊕ ((A1 ⊕ ¬A7)⊗ A2)
is λ-similar, with λ = 0.9951 to the original NN. For-
mula α misses the classification for 40 cases. Note
that the symbolic model is stable, the bad perfor-
mance of i
1
representation do not affect the model.
The CNN structure can codify the dataset with
100% accuracy. Bellow we present a prefect descrip-
tion for edible mushrooms.
0 1 1 −1 −1 0 0
0 1 −1 0 −1 −1 0
0 1 −1 0 −1 1 −1
1 1 −1 −1 −1 1 1
−1
0
−1
3
1 1 1 1
0
This structure have by interpretation the rule for edi-
ble mushrooms:
(A2.and.A3.and.NOT (A4).and.NOT (A5)).or.
(A2.and.NOT (A3).and.NOT (A5).and.NOT (A6)).or.
(A2.and.NOT (A3).and.NOT (A5).and.A6.and.NOT (A7)).or.
(A1.and.A2.and.NOT (A3).and.NOT (A4).and.NOT (A5).and.A6.and.A7)
6 CONCLUSIONS AND FUTURE
WORK
This methodology to codify and extract symbolic
knowledge from a NN is very simple and efficient for
the extraction of comprehensible rules from medium-
sized data sets. It is, moreover, very sensible to at-
tribute relevance.
In the theoretical point of view it is particularly
interesting that restricting the values assumed by neu-
rons weights restrict the information propagation in
the network, thus allowing the emergence of patterns
in the neuronal network structure. For the case of lin-
ear neuronal networks, having by activation function
the identity truncate to 0 and 1, these structures are
characterized by the occurrence of patterns in neu-
ron configuration directly presentable as formulas in
Łukasiewicz logic.
Generated fuzzy rules might do a good approxi-
mation of the data, but often are not interpretable. In
your point of view the interpretability of such sym-
bolic rules are strictly related to the type of fuzzy
logic associated to the problem. When we applied
our method on the extraction of rules from truth ta-
bles, generated on Product logic or on G
¨
odel logic,
this rules were very dificulte to interprete. For the ex-
traction of knowledge from this types of fuzzy logic
extraction processed governed by appropriated logic
must be developed.
We are using this methodology for fuzzy regres-
sion tree generation. Where we use CNN for finding
slitting formulas in the algorithm pruning fase (Al-
gara, 2007).
Acknowledgements
I tanks Helder Pita for reading and commenting on
the manuscript. I acknowledge the support of the In-
stituto Superior de Engenharia de Lisboa and the
´
Area
Cientifica da Matem
´
atica.
REFERENCES
Algara, E. (2007). Soft Operators Decision Trees: Un-
certainty and stability related issues. Vom Fachbere-
ich Mathematik der Technischen Universitt Kaiser-
slautern zur Verleihung des Akademischen Grades
Doktor der Naturwissenschaften, 2007.
Amato, P., Nola, A., and Gerla, B. (2002). Neural networks
and rational łukasiewicz logic. IEEE Transaction on
Neural Networks, vol. 5 no. 6, (2002)506-510.
Andersen, T. and Wilamowski, B. (1995). A modified re-
gression algorithm for fast one layer neural network
training. World Congress of Neural Networks, Wash-
ington DC, USA, Vol. 1 no. 4, CA, (1995)687-690.
Battiti, R. (1992). Frist- and second-order methods
for learning between steepest descent and newton’s
method. Neural Computation, Vol. 4 no. 2, (1992)141-
166.
Bello, M. (1992). Enhanced training algorithms, and in-
tehrated training/architecture selection for multilayer
This NN can be used to interprete formula:
IJCCI 2009 - International Joint Conference on Computational Intelligence
14
j
1
⊗ ¬ j
2
= (¬i
1
⊕ i
3
) ⊗ ¬(i
1
⊗ ¬i
2
⊗ ¬i
4
) = (¬(¬A4 ⊕ A7)⊕ A7) ⊗ ¬((¬A4 ⊕A7) ⊗
¬(A1 ⊗ A2 ⊗ ¬A4) ⊗¬(A2 ⊗ ¬A5 ⊗ ¬A6⊗ A7))) =
= ((A4 ⊗ ¬A7) ⊕A7) ⊗ ((A4 ⊗ ¬A7) ⊕(A1 ⊗ A2 ⊗ ¬A4)⊕ (A2 ⊗¬A5 ⊗ ¬A6 ⊗ A7)))
Some times the algorithm converged to un-
representable configurations like the one presented
below, with 100% accuracy. The frequency of this
type of configurations increases with the increase of
required accuracy.
Using rule R and selecting the best approximation in
data set to each un-representable formula, evaluated
in the data set, we have:
1. i
1
∼
0.9297
((¬A1 ⊗ A4)⊕ A2) ⊗¬A3 ⊗ ¬A6
2. i
3
∼
1.0
(A1 ⊕ ¬A7)⊗ A2
3. j
1
∼
0.9951
(i
1
⊗ ¬i
2
) ⊕ i
3
The extracted formula
α = (((((¬A1 ⊗A4) ⊕ A2) ⊗ ¬A3 ⊗ ¬A6) ⊗¬(A4 ⊗ A5 ⊗ ¬A7)) ⊕((A1 ⊕ ¬A7) ⊗ A2)
is λ-similar, with λ = 0.9951 to the original NN. For-
mula α misses the classification for 40 cases. Note
that the symbolic model is stable, the bad perfor-
mance of i
1
representation do not affect the model.
The CNN structure can codify the dataset with
100% accuracy. Bellow we present a prefect descrip-
tion for edible mushrooms.
0 1 1 −1 −1 0 0
0 1 −1 0 −1 −1 0
0 1 −1 0 −1 1 −1
1 1 −1 −1 −1 1 1
−1
0
−1
3
1 1 1 1
0
This structure have by interpretation the rule for
edible mushrooms:
(A2.and.A3.and.NOT (A4).and.NOT (A5)).or.
(A2.and.NOT(A3).and.NOT (A5).and.NOT (A6)).or.
(A2.and.NOT(A3).and.NOT (A5).and.A6.and.NOT (A7)).or.
(A1.and.A2.and.NOT (A3).and.NOT (A4).and.NOT (A5).and.A6.and.A7)
6 CONCLUSIONS AND FUTURE
WORK
This methodology to codify and extract symbolic
knowledge from a NN is very simple and efficient for
the extraction of comprehensible rules from medium-
sized data sets. It is, moreover, very sensible to at-
tribute relevance.
In the theoretical point of view it is particularly
interesting that restricting the values assumed by neu-
rons weights restrict the information propagation in
the network, thus allowing the emergence of patterns
in the neuronal network structure. For the case of lin-
ear neuronal networks, having by activation function
the identity truncate to 0 and 1, these structures are
characterized by the occurrence of patterns in neu-
ron configuration directly presentable as formulas in
Łukasiewicz logic.
Generated fuzzy rules might do a good approxi-
mation of the data, but often are not interpretable. In
your point of view the interpretability of such sym-
bolic rules are strictly related to the type of fuzzy
logic associated to the problem. When we applied
our method on the extraction of rules from truth ta-
bles, generated on Product logic or on G
¨
odel logic,
this rules were very dificulte to interprete. For the ex-
traction of knowledge from this types of fuzzy logic
extraction processed governed by appropriated logic
must be developed.
We are using this methodology for fuzzy regres-
sion tree generation. Where we use CNN for finding
slitting formulas in the algorithm pruning fase (Al-
gara, 2007).
ACKNOWLEDGEMENTS
I thanks Helder Pita for reading and commenting on
the manuscript. I acknowledge the support of the In-
stituto Superior de Engenharia de Lisboa and the
´
Area
Cientifica da Matem
´
atica.
REFERENCES
Algara, E. (2007). Soft Operators Decision Trees: Un-
certainty and stability related issues. Vom Fachbere-
ich Mathematik der Technischen Universitt Kaiser-
slautern zur Verleihung des Akademischen Grades
Doktor der Naturwissenschaften, 2007.
Amato, P., Nola, A., and Gerla, B. (2002). Neural networks
and rational łukasiewicz logic. IEEE Transaction on
Neural Networks, vol. 5 no. 6, (2002)506-510.
Andersen, T. and Wilamowski, B. (1995). A modified re-
gression algorithm for fast one layer neural network
training. World Congress of Neural Networks, Wash-
ington DC, USA, Vol. 1 no. 4, CA, (1995)687-690.
Battiti, R. (1992). Frist- and second-order methods
for learning between steepest descent and newton’s
method. Neural Computation, Vol. 4 no. 2, (1992)141-
166.
Bello, M. (1992). Enhanced training algorithms, and in-
tehrated training/architecture selection for multilayer
perceptron network. IEEE Transaction on Neural Net-
works, vol. 3, (1992)864-875.
Bornscheuer, S., H
¨
olldobler, S., Kalinke, Y., and
Strohmaier, A. (1998). Massively parallel reasoning.
in: Automated Deduction - A Basis for Applications,
Vol. II, Kluwer Academic Publisher, (1998)291-321.
REVERSE ENGINEERING AND SYMBOLIC KNOWLEDGE EXTRACTION ON AUKASIEWICZ LOGICS USING
NEURAL NETWORKS
15
Castro, J. and Trillas, E. (1998). The logic of neural
networks. Mathware and Soft Computing, vol. 5,
(1998)23-27.
Charalambous, C. (1992). Conjugate gradient algorithm for
efficient training of artificial neural networks. IEEE
Proceedings, Vol. 139 no. 3, (1992)301-310.
d’Avila Garcez, A. S. (2007). Advances in neural-symbolic
learning systems: Modal and temporal reasoning.
In B. Hammer and P. Hitzler (ed.), Perspectives of
Neural-Symbolic Integration, Studies in Computa-
tional Intelligence, Volume 77, Springer, 2007.
d’Avila Garcez, A. S., Lamb, L. C., and Gabbay, D. M.
(2008). Neural-simbolic Cognitive Reasoning. Cog-
nitive Technologies, Springer.
Dubois, D. and Prade, H. (2000). Fundamentals of fuzzy
sets. Kluwer, 2000.
Eklund, P. and Klawonn, F. (1992). Neural fuzzy logic pro-
gramming. IEEE translations on neural networks, Vol.
3, No. 5, 1992.
Fiadeiro, J. and Lopes, A. (1997). Semantics of architec-
tural connectors. TAPSOFT’97 LNCS, v.1214, p.505-
519, Springer-Verlag, 1997.
Frank, M. (1979). On the simultaneous associativity of
f (x, y) and x + y − f (x, y). Aequations Math., vol. 19,
(1979)194-226.
Fu, L. (1993). Knowledge-based connectionism from revis-
ing domain theories. IEEE Trans. Syst. Man. Cybern,
Vol. 23 ,(1993)173-182.
Gallant, S. (1988). Connectionist expert systems. Commun.
ACM, Vol. 31 ,(1988)152-169.
Gallant, S. (1994). Neural Network Learning and Expert
Systems. Cambridge, MA, MIT Press.
Gerla, B. (2000). Functional representation of many-valued
logics based on continuous t-norms. PhD thesis, Uni-
versity of Milano, 2000.
Hagan, M., Demuth, H., and Beal, M. (1996). Neural Net-
work Design. PWS Publishing Company, Boston.
Hagan, M. and Menhaj, M. (1999). Training feedforward
networks with marquardt algorithm. IEEE Transac-
tion on Neural Networks, vol. 5 no. 6, (1999)989-993.
H
´
ajek, P. (1995). Fuzzy logic from the logical point of view.
In Proceedings SOFSEM’95, LNCS, Springer-Verlag,
1995.
Hassibi, B., Stork, D., and Wolf, G. (1993). Optimal brain
surgeon and general network pruning. IEEE Interna-
tional Conference on Neural Network, vol. 4 no. 5,
(2003)740-747.
Hitzler, P., H
¨
olldobler, S., and Seda, A. (2004). Logic pro-
grams and connectionist networks. Journal of Applied
Logic, 2, (2004)245-272.
H
¨
olldobler, S. (2000). Challenge problems for the inte-
gration of logic and connectionist systems. in: F.
Bry, U.Geske and D. Seipel, editors, Proceedings 14.
Workshop Logische Programmierung, GMD Report
90, (2000)161-171.
H
¨
olldobler, S. and Kalinke, Y. (1994). Towards a new
massively parallel computational model for logic pro-
gramming. in: Proceedings ECAI94 Workshop on
Combining symbolic and Connectionist Processing,
(1994)68-77.
H
¨
olldobler, S., Kalinke, Y., and St
¨
orr, H. (1999). Approx-
imating the semantics of logic programs by recurrent
neural networks. Applied Intelligence 11, (1999)45-
58.
Jacobs, R. (1988). Increased rates of convergence through
learning rate adaptation. Neural Networks, Vol. 1 no.
4, CA, (1988)295-308.
Komendantskaya, E., Lane, M., and Seda, A. K. (2007).
Connectionistic representation of multi-valued logic
programs. In B. Hammer and P. Hitzler (ed.), Perspec-
tives of Neural-Symbolic Integration, Studies in Com-
putational Intelligence, Volume 77, Springer, 2007.
Mehrotra, K., Mohan, C., and Ranka, S. (1997). Elements
of Artificial Neural Networks. The MIT Press.
Miniani, A. and Williams, R. (1990). Acceleration of
back-propagation through learning rate and momen-
tum adaptation. Proceedings of International Joint
Conference on Neural Networks, San Diego, CA,
(1990)676-679.
Samad, T. (1990). Back-propagation improvements based
on heuristic arguments. Proceedings of International
Joint Conference on Neural Networks, Washington
(1990)565-568.
Solla, S., Levin, E., and Fleisher, M. (1988). Acceler-
ated learning in layered neural networks. Complex
Sustems, 2, (1988)625-639.
Towell, G. and Shavlik, J. (1993). Extracting refined
rules from knowledge-based neural networks. Mach.
Learn., Vol. 13 ,(1993)71-101.
Towell, G. and Shavlik, J. (1994). Knowledge-based artifi-
cial neural networks. Artif. Intell., Vol. 70 ,(1994)119-
165.
IJCCI 2009 - International Joint Conference on Computational Intelligence
16