AN ADAPTIVE SWARM-BASED ALGORITHM FOR RESOURCE

ALLOCATION IN DYNAMIC ENVIRONMENTS

Tony White, Amirali Salehi-Abari and Gayan Abeysundara

School of Computer Science, Carleton University, Ottawa, Canada

Keywords:

Swarm Intelligence, Task Allocation.

Abstract:

Dynamic allocation of agents to a set of tasks is a hard problem. Furthermore, having too few or too many

agents can result in poor task completion owing to conﬂicting agent decisions thus creating the problem of

the Tragedy of the Commons. This paper proposes a swarm-based algorithm inspired by the social behavior

of ants that causes agent specialization to a particular task – resource allocation in a spatial region – and

determines the near optimal number of agents required to complete the tasks presented. The utility of the

algorithm is demonstrated by application to the dynamic allocation of frequencies in a cellular network.

1 INTRODUCTION

The principal components in a system employing

swarm intelligence are the agents and the environment

being controlled. Each agent follows a simple set of

rules designed for the environment being controlled.

Agents interact with each other locally and the envi-

ronment to determine its course of action. Each agent

has only partial information about the environment

and is unaware of what the entire swarm is doing,

leading to no overall global evaluation. However, as

a result of the overall swarm behavior from each and

every agent intertwined with each other, the system

self-organizes to produce an efﬁcient working entity

(Bonabeau et al., 1999).

Cell networks are an example of a hard control

problem where cell frequencies represent limited re-

sources that can be allocated to consumers (callers)

using the network. Callers use the frequencies avail-

able within a cell to make calls and change the fre-

quencies that they use as they move from one cell

to another. It is the position of this paper that a

swarm-based control system can efﬁciently allocate

such limited resources. As such, in the control prob-

lem described in this paper, agents distribute the lim-

ited number of cellular frequencies among the cells to

accommodate network ﬂuctuations and areas of high

frequency utilization.

The speciﬁc strategy used in the proposed agent-

based solution is referred to as division of labor and

recruitment. Over time, agents in the system estab-

lish a routine, or pattern, to efﬁciently divide the to-

tal workload, or stimulus, among the agent popula-

tion. Furthermore, this is accomplished by using dy-

namic response thresholds that change depending on

demand. Cells that are in high demand and low on

resources stimulate agents until one agent responds.

Each stimulated agent determines if it will respond to

the cell depending on its response threshold and la-

tency (or think time) considerations. Each agent has

a unique response threshold for each cell in the net-

work. There is an indirect transfer of information be-

tween agents, or so-called stigmergy, because when

an agent responds to a cell in need it changes the en-

vironment by decreasing that stimulus for others.

In designing a swarm system based upon division

of labor and recruitment, two problems need to be

solved. First, an algorithm for redeployment of re-

sources in the environment needs to be created. Sec-

ond, an algorithm for dynamically adjusting the num-

ber of agents involved in the redeployment process

is required. Without the latter, a shortfall of agents

can cause the system to react too slowly to changes

in demand; however, with too many agents, agent de-

cision making can cause conﬂicts leading to unsatis-

factory oscillatory resource allocation. The need for

these two algorithms motivates the work reported in

this paper.

The paper proceeds as follows. Section 2 de-

scribes the resource allocation algorithms that solve

the two questions highlighted in the previous para-

graph. Section 3 provides a brief description of the

183

White T., Salehi-Abari A. and Abeysundara G. (2009).

AN ADAPTIVE SWARM-BASED ALGORITHM FOR RESOURCE ALLOCATION IN DYNAMIC ENVIRONMENTS.

In Proceedings of the International Joint Conference on Computational Intelligence, pages 183-188

DOI: 10.5220/0002285601830188

 SciTePress

dynamic frequency assignment problem, highlighting

call models. Sections 4 and 5 describe experimental

setup and results respectively, while Section 5 shows

results for the call models introduced in Section 3.

Section 6 discusses the results highlighting the suc-

cess of the Dynamic Agent Population algorithm. Fi-

nally, Section 8 summarizes the key messages of the

paper and indicates potential future research direc-

tions.

2 ALGORITHMS

There are two distinct algorithms for resource alloca-

tion described in this paper. The ﬁrst relates to divi-

sion of labor: making agents specialize in particular

locations in the environment. The second is related

to the size of the agent population itself. These algo-

rithms are described in the next two subsections.

2.1 Division of Labor

The division of labor model consists of a set of

decision-making agents, a

, responding to a set of

stimulii, S

, moving within an environment, E, con-

sisting of a collection of N cells of a giventopology,T.

The N cells contain resources, R

. The total number

of resources present within the environment is con-

stant. Resources may be reallocated to cells by agents

based upon a set of constraints, C

. Agents may be

in the idle, thinking or working states. When in the

thinking or working states an agent is responding to

a stimulus in a speciﬁc cell, l. When responding to

a stimulus to reallocate resources, an agent, a, ﬁrst

thinks about the decision to reallocate resources avail-

able within the target cell and neighborhood. It does

this in order to ensure that resource reallocation does

not occur too quickly in the network potentially caus-

ing instability. When the agent thinking time expires,

it enters the working state and it executes a realloca-

tion algorithm, A

, which may cause resources to be

moved from neighboring cells to the target cell. The

reallocation algorithm terminates when resources are

reallocated which results in lowering the stimulus be-

low a threshold, Thd, or a timeout, T, occurs. When

the algorithm terminates, the agent reenters the idle

state.

Adaptive task allocation consists of agents adapt-

ing and learning to perform certain tasks of the overall

stimulus. Each agent, a, maintains a set of response

thresholds, θ

, for each cell, j, in the environment.

The system adapts by changing response thresholds

depending on cell stimulation. If an agent responds

to a cell in demand, it will lower its threshold for that

cell by ξ

and its neighboring cells by ξ

, and increas-

ing its threshold for all other cells by ϕ. Therefore,

agents are able to specialize in particular areas of the

grid where they have done more work, and have lower

response thresholds. As demand patterns are not com-

pletely random – where they follow some sort of pat-

tern or trend over time – agents specializing in areas

of the environment produces a ﬂexible system that can

adapt to changing conditions. Agents satisfy demands

(reduce stimulus) by moving resources around among

neighboring cells subject to the aforementioned con-

straints.

When a cell experiences high resource usage it

broadcasts a message to all available agents, stimu-

lating each one. The probability that an idle agent a

located in cell cell(a) responds to a stimulus from cell

j is:

+ αθ

+ βthink

cell(a) j

(1)

Where S

is the amount of demand or stimulus

from cell j, θ

is the response threshold of agent a

for cell j, think

cell(a) j

is the thinking time for agent

a and cell j, and α and β are two positive coefﬁcients

that weight the inﬂuences of θ and d respectively. The

thinking time is a function of the rate of change of uti-

lization of resources in the cell. An agent in the think-

ing state may respond to a stimulus in a neighboring

cell. Several agents may respond to the stimulus, the

cell randomly selects from those responding; the oth-

ers are ignored. If an agent a in the idle state responds

to a stimulus from cell j, it updates its response thresh-

olds in the following way:

← θ

− ξ

(2)

an( j)

← θ

an( j)

− ξ

, for ∀n( j) (3)

← θ

+ ϕ, for ∀k 6= j and k /∈ {n( j)} (4)

Where n( j) is the set of neighboring cells to cell

j, ξ

and ξ

are two system-wide learning coefﬁcients

corresponding to cell j and its neighbors respectively,

and ϕ is the forgetting coefﬁcient for all other cells

in the environment. Once an agent has received the

acknowledgment to take on the task it changes its

state to thinking and begins to decrement its think-

ing time timer. When the timer expires, the agent

changes state to working and executes its resource

allocation algorithm, A

. The resource allocation al-

gorithm for the cell network problem is described in

Section 3.2. Equations 2, 3 and 4 are motivated by

(Theraulaz et al., 1990; Bonabeau et al., 1998); the

thinking time term being the difference.

IJCCI 2009 - International Joint Conference on Computational Intelligence

184

2.2 Dynamic Agent Population

The Dynamic Agent Population (DAP) algorithm is

based upon agent response thresholds. At every clock

tick, each agent will calculate its average response

threshold (represented by the avgθ function in the Dy-

namic Agent Population Algorithm). If the average

response threshold of an idle agent (represented by

the isIdle function) is below a minimum threshold

value, Th

min

, indicating the agent is not being used,

it will remove itself from the system. If an agent, in

any state, has an average response threshold above a

certain value, Th

max

, it will spawn a new agent, or

duplicate itself. The new agent will be located in the

same cell as the original. Values for Th

max

and Th

min

are in the range of [0,100]. According to Equations 2,

3 and 4, agent response thresholds only change when

an agent moves from the idle to the thinking state.

Therefore, an agent that is never stimulated continues

to have the same response threshold that it was ini-

tialized with, θ

initial

. In order to provide for agent ter-

mination, all agents have all of their response thresh-

olds decay by δ at every time tick. So, over a period

of time, an agent remaining in the idle state in a low-

demand environment will reduce its average threshold

until it terminates itself.

Algorithm 1: Dynamic Agent Population Algorithm.

1: for all agents a do

2: if a.isIdle then

3: for j = 1 to N do

4: θ

← θ

× (1− δ)

5: end for

6: end if

7: if a.avgθ < Th

min

then

8: remove a

9: end if

10: if a.avgθ > Th

max

then

11: create new agent a

′

at location of agent a

12: provide a

′

with θ

initial

response thresholds

13: end if

14: end for

When the Dynamic Agent Population Algorithm,

as presented in Algorithm 1, is used, the initial agent

population is set to 1; agents are rapidly created

as the single agent quickly becomes overwhelmed

responding to stimuli. Experiments were undertaken

with varying initial population sizes, however the

population converged to the same size given a

sufﬁcient time.

3 DYNAMIC FREQUENCY

ASSIGNMENT

A cellular network consists of many cells. In order

to make a cellular call, a caller must be allocated a

channel within a particular cell. Each cell has a ﬁnite

number of channels to allocate, once exhausted new

calls are either blocked or existing calls are dropped

as the caller moves from one cell to another, releas-

ing one channel and acquiring another. Channel as-

signment is hard in that the frequencies required for

a channel cannot be reused in adjacent cells owing

to interference. In order to make a call, a channel

is needed. A channel is composed of the three fre-

quencies required for communication. In this paper

we use the words channel and frequency interchange-

ably, which is a signiﬁcant simpliﬁcation. Calls are

generated depending on a user speciﬁed call genera-

tion rate. The call generation rate, or call rate, does

not give the number of calls per second, but only pro-

vides an upper bound on the number of call that can

be generated in a second. The actual number of calls

per second is a random number uniformly distributed

between zero and the call rate. A newly generated

call is positioned on the grid according to a hotspot

algorithm – explained in sections 3.1.1-3.1.3. The

hotspot algorithm also determines the call direction.

The holding time of a call and its velocity in the net-

work are randomly determined. Handoffs occur when

a call moves from one cell to another, and a suitable

channel is allocated in the new cell.

3.1 Call Models

To depict realistic situations in the cellular simulation,

multiple call models were created. They are: Down-

town, Centre Hotspot, and Random Hotspot.

3.1.1 Downtown

The Downtown call model represents a simpliﬁed ver-

sion of a typical workday in a city. The call model

consists of four cycles, each lasting an equal amount

of time. The ﬁrst cycle represents the morning, where

people are moving into the city centre. Calls in this

cycle have a direction toward the centre, and have a

random call location that is partially centre-oriented;

i.e., directed towards the city centre. The second cycle

represents the working afternoon, where most people

are densely populated in the centre of a city. In this

cycle, calls are generated in the centre and have a ran-

dom direction. The third cycle represents the end of

day where people are traveling back home. The cycle

generates calls with an outward direction and a loca-

AN ADAPTIVE SWARM-BASED ALGORITHM FOR RESOURCE ALLOCATION IN DYNAMIC ENVIRONMENTS

185

tion that is partially centre-oriented. The last cycle of

the Downtown call model represents the evening, with

no clear pattern or trend.

3.1.2 Centre Hotspot

The Centre Hotspot call model represented by two cy-

cles. The ﬁrst generates calls with a random location

and direction. The second cycle generates calls that

are densely populated in the centre, with an inward

moving direction.

3.1.3 Random Hotspot

This call model is very similar to the Centre Hotspot,

but the hotspot location is randomly determined in-

stead of centre-oriented.

3.2 Resource Allocation Algorithm

In the application of the algorithms in Section 2, the

resources to be reallocated are now frequencies. The

reallocation algorithm, A

, for dynamic frequency al-

location is presented in Algorithm 2.

Algorithm 2: Reallocation Algorithm(agent).

1: if agent.cell.demand < Thd then

2: Set agent state to idle

3: else

4: for all cell j ∈ agent.cell.neighbors do

5: if cell j has unused resources > DR

min

then

6: while cell j has more frequencies do

7: if next available frequency, freq, is not

used in agent.cell and its other neigh-

bors then

8: transfer freq to agent.cell

9: return

10: end if

11: end while

12: end if

13: end for

14: end if

The DR

min

value is included in the algorithm in

order to ensure that a neighborhood cell will always

retain a minimum number of resources. The reallo-

cation algorithm is executed once per time tick and

may execute a maximum of T times before the agent

is forced to return to the idle state. This ensures two

things. First, an agent can move frequencies over sev-

eral time ticks and second, an agent will not get stuck

in a cell indeﬁnitely trying to reallocate frequencies.

Frequencies are moved one at a time in order to en-

sure that agents working in adjacent or nearby cells

can effectively share available frequency resources.

4 EXPERIMENTAL SETUP

In the experiments that were conducted, the param-

eters shown in Table 1 were common to all runs.

Experimental sets of 50 runs were conducted for

each of the call models described in sections 3.1.1 to

3.1.3 with the Dynamic Agent Population algorithm

(Algorithm 1) switched on and off. With the Dy-

namic Agent Population (DAP) algorithm switched

off, agent populations were run for values of 0, 1, 5,

10, 15, 20, 25, 30, 35, and 40 agents. A population of

zero agents was included as a control case implying

static allocation of frequencies.

The mean call holding time was 180 seconds with

a distribution between 5 and 1500 seconds. Call

velocity was uniformly distributed between 0 and

0.02 cells/second, implying that approximately3 cells

would be traversed in an average call. Experiments

were conducted with an average call generation rate

of 3/second up to 10/second. Each simulation was

run for 12,000 seconds, and results averaged over all

runs.

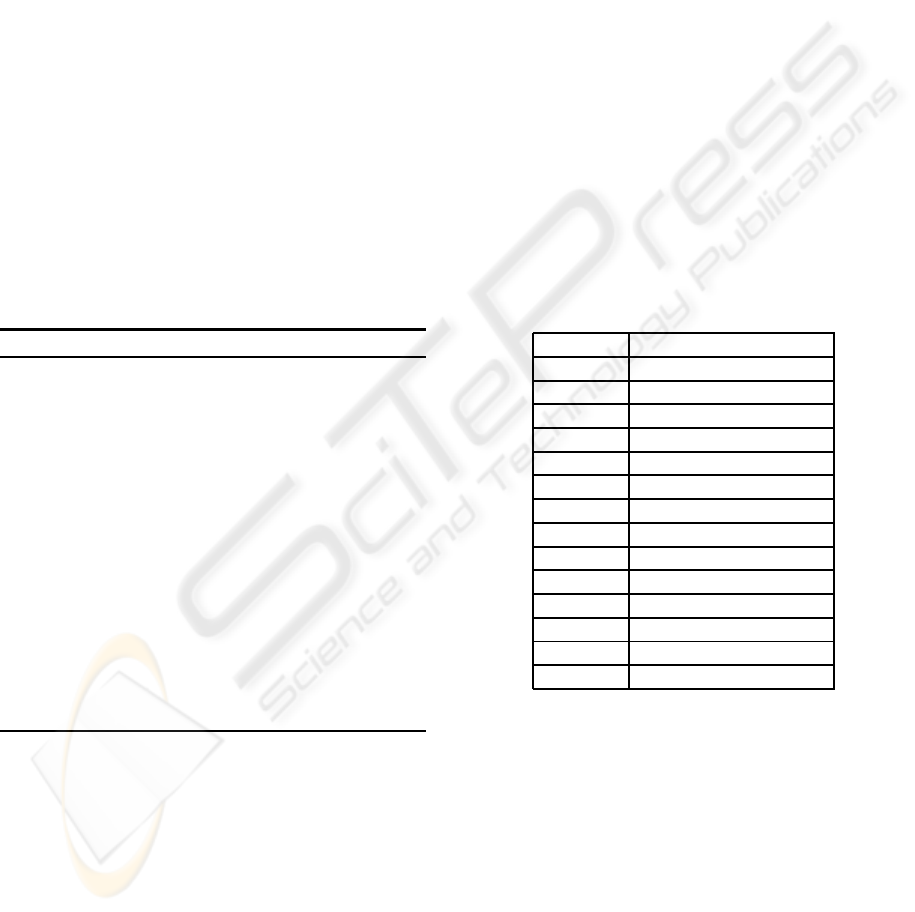
Table 1: Experimental Parameters.

Variable Value

min

max

80%

N 100

R 10 frequencies per cell

initial

Thd 65%

min

T 30

δ 0.05

α 0.5

β 50

ϕ 0.5

5 RESULTS

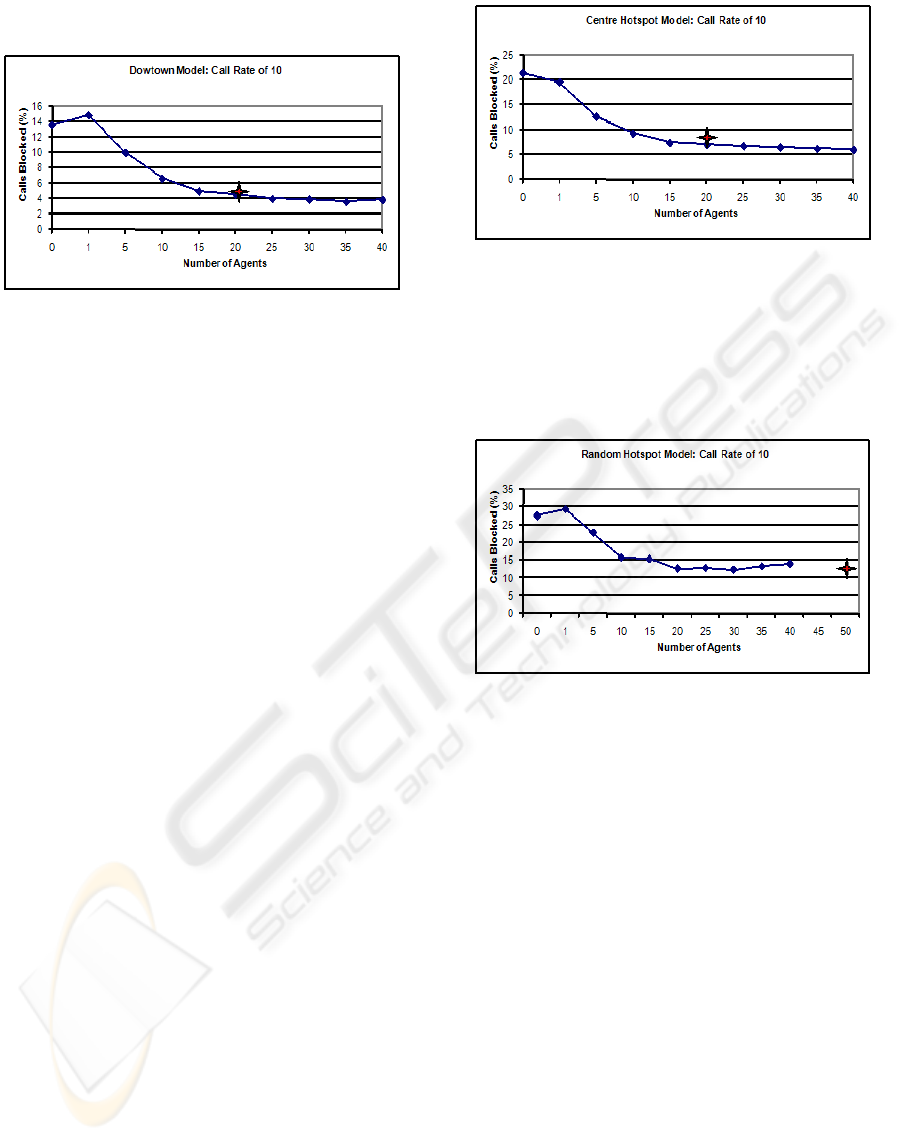
The simulation results are shown in the following

graphs, grouped by the call model used. Each graph

shows the relationship between the number of agents

used (horizontal axis) and the percentage of calls

blocked (vertical axis). Each graph contains a star that

represents the results of the DAP algorithm. The point

of intersection depicted by the star represents the ﬁnal

number of agents at the end of the simulation and the

percentage of calls blocked.

IJCCI 2009 - International Joint Conference on Computational Intelligence

186

5.1 Downtown Model

Figure 1: Downtown Model: Call Rate of 10.

Figure 1 shows the variation of call blocking percent-

age with number of agents for the Downtown model.

As more agents were added to the system, the percent-

age of calls started to level off into a plateau. The only

non-monotonic behaviour seen was when one agent

supported the network. Furthermore, as the call rate

increased, the ﬂuctuation grew larger (not shown).

This is nothing to be concerned about since one agent

is not considered a swarm and should not necessar-

ily produce better results. In the situations where the

lone agent produced worse results, the cause is due to

an agent moving frequencies from a cell into which

active callers are just about to move, thereby causing

a blocked handoff. It could also be possible that with

such high call rates, the agent was shufﬂing channels

in a way that caused more calls to be blocked. Con-

sidering the above call rates of ﬁve to ten calls per

second, the agent-based solution reduced the number

of calls blocked by 69% = 1-(1.91/6.3) to 71% = 1-

(3.89/13.47). The DAP algorithm converged on the

optimal number of agents that produced the lowest

call blocking rate. The number of calls blocked was

reduced by an average of 67% using dynamic agents.

The adaptive population neither affects the number of

completed calls nor the number of handoffs.

5.2 Centre Hotspot Call Model

Figure 2 shows the variation of call blocking percent-

age with the number of agents for the Centre Hotspot

model.

All scenarios with one agent showed a lower

number of blocked calls than the agent-less system.

One other interesting discovery of this call model

is how uniform the graphs are when compared with

the Downtown model. This is most likely because

there are fewer cycles than the Downtown model, and

gave the agents more time to adapt and settle into

the predictable pattern. Simulations with the Centre

Figure 2: Centre Hotspot Call Model: Call Rate of 10.

Hotspot model produced a 71% - 82% reduction in

calls blocked.

5.3 Random Hotspot Call Model

Figure 3: Random Hotspot Model: Call Rate of 10.

Figure 3 shows the variation of call blocking per-

centage with the number of agents for the Random

Hotspot model. Adding agents in the network did

lower the call blocking rate until it leveled off, but

there were more ﬂuctuations. This is mainly be-

cause the hotspot was always in a random location

every cycle. The agents were unable to adapt to net-

work conditions as easily as the other two centre-

oriented call models. Consequently,more ﬂuctuations

in the results should be expected. Agents in this call

model reduced the number of calls blocked by 55%

- 77%. When using DAP, it sometimes resulted in

more agents in the system than required. However,

DAP did result in a call blocking rate that was close to

the minimum that was obtained using a ﬁxed number

of agents. We hypothesize that the random hotspots

produced a high demand for agents that resulted in

higher agent populations, but did not result in better

call rates simply because the network is too stressed

and could not be relieved by extra channel shufﬂing.

Using DAP, the call blocking rate was reduced by an

average of 62%.

AN ADAPTIVE SWARM-BASED ALGORITHM FOR RESOURCE ALLOCATION IN DYNAMIC ENVIRONMENTS

187

6 DISCUSSION

We can conclude that adding agents to the cellular

network produced better call rates under all condi-

tions. Agents self-organize to reduce the percentage

of calls blocked signiﬁcantly. Considering all call

models, agents were able to reduce the number of

calls blocked by 55% - 82%. On average, the agent-

based solution decreased the number of calls blocked

by a remarkable 72%. Call generation rate had no ef-

fect on the qualitative results. With a high call rate of

10, when one assumes the network may be too over-

loaded to have any affect, the addition of agents al-

ways improved network performance. Another inter-

esting fact was when the simulation results attained

the minimum call blocking rate, the addition of more

agents did not overload the system but continued to

produce the same performance results. Although the

Random Hotspot model generated more ﬂuctuations,

the agents adapted efﬁciently to the continuous ﬂow

of random network hotspots.

The DAP algorithm was extremely good, produc-

ing call rates that were as good as any of the ﬁxed

agent methods. It managed to adapt to a minimal

number of agents under most situations, with the ex-

ception of the Random Hotspot were slightly more

agents were utilized. Even so, call rate results were

not affected. An average reduction in blocked calls

in excess of 62% was achieved using the DAP algo-

rithm, considering all call models and call rates; a sta-

tistically signiﬁcant difference.

7 RELATED WORK

Al agha (Al agha, 2000) proposes a multi-agent so-

lution for intelligent base stations resource allocation

in wireless networks. Agents are able to combine

knowledge and experience with neighboring agents to

make the best decisions. This is achieved by agents

cooperating, communicating, reasoning, and perceiv-

ing. Agents corresponding with a base station are

capable of communicating its state to neighbors and

learning from past events in the environment to opti-

mize the utilization of resources. The agent solution is

used in conjunction with a resource allocation scheme

known as Channel Segregation (CS). Channel Seg-

regation differs from traditional dynamic allocation

schemes because it has a simple form of self-learning.

It involves segregating physical channels from a com-

mon pool by each base station to form a preferred list

of channels. Base stations attempt to allocate chan-

nels at the top of their priority list. The learning as-

pect of CS is achieved though the way in which prior-

ity lists are formed, resulting in differing lists across

the network cells - and stabilizing over time. Simu-

lation results have shown that the integration of intel-

ligent agents with channel segregation had improved

call rates by decreasing the number of calls blocked.

An overview of research done in the ﬁeld of both

Communication Networks (CN) and Distributed Arti-

ﬁcial Intelligence (DAI) can be found in (Hayzelden

and Bigham, 1999). Articles in (Hayzelden and

Bigham, 1999) identify current trends in agent-based

network control and management. They discuss ar-

eas that would most beneﬁt from agent technologies

and deployment strategies for agent-based solutions,

some of which are ant-based.

8 CONCLUSIONS

This paper has demonstrated that an adaptive popu-

lation of agents using principles from swarm intelli-

gence can effectively allocate resources in a dynamic

environment.

The resizing algorithm can be thought of as a re-

cruitment algorithm.

Using division of labor and adaptive task alloca-

tion, agents modeled after social insects produced a

decentralized, robust, and adaptive system. The sim-

ple interconnected agents were able to self-organize

and exhibit intelligent behavior to dramatically de-

crease blocked call rates.

We propose that future work should include agent-

to-agent communication. This may be accomplished

by agents simulating other agents, or cooperative ne-

gotiation between agents. The latter possibility was

a proposed solution by Bigham, where agents asso-

ciated with the cellular base station would negotiate

with other agents to optimize local cell coverage (Du

et al., 2003).

REFERENCES

Al agha, K. M. (2000). Resource management in wire-

less networks using intelligent agents. Int. J. Netw.

Manag., 10(1):29–39.

Bonabeau, E., Dorigo, M., and Theraulaz, G. (1999).

Swarm Intelligence: From Natural to Artiﬁcial Sys-

tems. Oxford.

Bonabeau, E., Theraulaz, G., and Deneubourg, J.-L. (1998).

Fixed response thresholds and the regulation of divi-

sion of labor in insect societies. Working Papers 98-

01-009, Santa Fe Institute.

Du, L., Bigham, J., Cuthbert, L., Nahi, P., and Parini, C.

(2003). Intelligent cellular network load balancing

IJCCI 2009 - International Joint Conference on Computational Intelligence

188

using a cooperative negotiation approach. volume 3,

pages 1675–1679 vol.3.

Hayzelden, A. L. and Bigham, J., editors (1999). Software

Agents for Future Communication Systems. Springer-

Verlag New York, Inc., Secaucus, NJ, USA.

Theraulaz, G., Goss, S., Gervet, J., and Deneubourg, J.-L.

(1990). Task differentiation in polistes wasp colonies:

a model for self-organizing groups of robots. In Pro-

ceedings of the ﬁrst international conference on sim-

ulation of adaptive behavior on From animals to an-

imats, pages 346–355, Cambridge, MA, USA. MIT

Press.

AN ADAPTIVE SWARM-BASED ALGORITHM FOR RESOURCE ALLOCATION IN DYNAMIC ENVIRONMENTS

189