
A MULTI-VALUED NEURON
WITH A PERIODIC ACTIVATION FUNCTION
Igor Aizenberg
Department of Computer Science, Texas A&M University-Texarkana, P.O. Box75505- 5518, Texarkana, TX 75505, U.S.A.
Keywords: Complex-valued neural networks, Derivative-free learning, Pattern recognition, Classification.
Abstract: In this paper, a new activation function for the multi-valued neuron (MVN) is presented. The MVN is a
neuron with complex-valued weights and inputs/output, which are located on the unit circle. Although the
MVN has a greater functionality than a sigmoidal or radial basis function neurons, it has a limited capability
of learning highly nonlinear functions. A periodic activation function, which is introduced in this paper,
makes it possible to learn nonlinearly separable problems and non-threshold multiple-valued functions using
a single multi-valued neuron. The MVN’s functionality becomes higher and the MVN becomes more
efficient in solving various classification problems. A learning algorithm based on the error-correction rule
for an MVN with the introduced activation function is also presented.
1 INTRODUCTION
The discrete multi-valued neuron (MVN) was
introduced by Aizenberg N. and Aizenberg I.
(1992). This neuron operates with complex-valued
weights. Its inputs and output are located on the unit
circle, and for a discrete MVN they are exactly k
th
roots of unity (where k is a positive integer).
Therefore the MVN's activation function, which was
proposed by Aizenberg N., Ivaskiv and Pospelov
(1971), depends only on the argument (phase) of the
weighted sum. In fact, the discrete MVN utilizes
general principles of multiple-valued threshold logic
over the field of complex numbers. These principles
were introduced by Aizenberg N. and Ivaskiv (1977)
and then developed and deeply considered by
Aizenberg I., Aizenberg N. and Vandewalle (2000).
The key point of this theory is that the values of k -
valued logic are encoded by the k
th
roots of unity.
Therefore a function of k -valued logic maps a set of
the k
th
roots of unity on itself.
The discrete MVN has two learning algorithms
that are presented in detail in (Aizenberg I. et al.,
2000). They are based on simple linear learning
rules and are derivative-free, what makes them
highly efficient. This property and the MVN's high
functionality made this neuron attractive for the
development of different applications. We have to
mention among others several associative memories
with a different topology: the cellular memory
(Aizenberg N. and Aizenberg I., 1992), the
Hopfield-like memories (Jankowski, Lozowski and
Zurada, 1996), (Muezzinoglu, Guzelis and Zurada,
2003), (Lee, 2001, 2004), the memories for storing
medical images (Aoki and Kosugi, 2000), (Aoki,
Watanabe, Nagata and Kosugi, 2001), and the
memory with random connections (Aizenberg I. et
al., 2000). The MVN was also used as a basic
neuron in a cellular neural network (Aizenberg I.
and Butakoff C., 2002).
In (Aizenberg I., Moraga and Paliy, 2005), a
continuos MVN was proposed. In the same paper, it
was suggested to use the MVN as a basic neuron in a
feedforward neural network. This network, which
can consist of both continuous and discrete MVNs,
and its derivative-free backpropagation learning
algorithm were explicitly presented in (Aizenberg I.
and Moraga, 2007). Aizenberg I., Paliy, Zurada and
Astola (2008) have generalized this learning
algorithm for a network with an arbitrary amount of
output neurons. Since a single MVN is more flexible
and has a higher fucntionality than, for example,
sigmoidal or radial-basis function neurons, the
MVN-based feedforward neural network also has a
much higher functionality, learns faster, and
generalizes better than a traditional feedforward
network and kernel-based networks when solving
both benchmark and real world problems (Aizenberg
I. and Moraga, 2007), (Aizenberg I. et al., 2008).
347
Aizenberg I. (2009).
A MULTI-VALUED NEURON WITH A PERIODIC ACTIVATION FUNCTION.
In Proceedings of the International Joint Conference on Computational Intelligence, pages 347-354
DOI: 10.5220/0002286203470354
Copyright
c
SciTePress

However, it is still very attractive to increase the
functionality of a single neuron, which in turn will
make it possible to solve highly nonlinear problems
of pattern recognition and modeling using simpler
networks.
In this paper, we consider a multi-valued neuron
with a modified discrete activation function, which
is k-periodic. As it was mentioned above, the
discrete MVN can learn the k-valued threshold
functions or the threshold functions of k-valued logic
(Aizenberg N. and Ivaskiv, 1977), (Aizenberg I. et
al., 2000). However, it is clear that the k-valued
threshold functions form just a small subset of the k-
valued functions. This means that those functions
that are not threshold can not be learned using a
single MVN. The question is: if some k-valued
function f is not a k-valued threshold function, can it
be a partially defined m-valued threshold function
for some m>k? If so, it is possible to learn this
function using a single MVN, but with an m-valued
activation function instead of a k-valued activation
function.
We will show here one of the possible ways of
finding such m>k that a k-valued function, which is
not a k-valued threshold function, will become an m-
valued threshold function. Therefore, while this
function can not be learned using a single k-valued
MVN, it will be possible to learn it using a single m-
valued MVN.
The idea behind our approach is similar to the
idea, on which a universal binary neuron (UBN) is
based. The UBN was introduced in (Aizenberg I.,
1991) and then developed in (Aizenberg I. et al.,
2000) and (Aizenberg I., 2008). It is a neuron with
complex-valued weights and an activation function,
which separates the complex plane into m equal
sectors determining the output by the alternating
sequence of 1,-1,1,-1,… depending on the parity of
the sector’s number. When m=2, the functionality of
the UBN coincides with the functionality of a
classical neuron with a threshold activation function
(Aizenberg I. et al., 2000). However, if m>2, the
functionality of the UBN is always higher than that
of a classical threshold neuron. Thus, when m>2, the
UBN can learn non-threshold (nonlinearly
separable) Boolean functions. In fact, such a
definition of the UBN activation function may be
considered as an l-multiple duplication of the
sequence {1,-1} and of the sectors into which the
complex plane is divided, respectively. Hence
2ml=
is the total number of sectors in the UBN
activation function. If
2l >
then the single UBN
may learn nonlinearly separable Boolean functions.
In this paper, we suggest to use a similar
approach to increase an MVN’s functionality. If
there is some function
()
1
,...,
n
f
xx of k-valued
logic, but this function is not a threshold function of
k-valued logic and therefore it can not be learned
using a single discrete MVN with a regular k-valued
activation function, we suggest to consider the initial
function in m-valued logic, where
mkl= . By
analogy with the UBN, the complex plane will be
devided onto
mkl
=
sectors and the MVN’s
activation function in this case becomes l-multiple
and k-periodic. We will define it below. Then we
will consider a learning algorithm for the MVN with
this activation function. Finally, we will demonstrate
how a modified single MVN may learn problems
which can not be learned using a traditional single
MVN. This may dramaticly simplify solving many
different classification problems. For the readrer’s
convenience we will start from a brief reminder
about the MVN, UBN, and their learning algorithms.
2 MULTI-VALUED AND
UNIVERSAL BINARY
NEURONS
2.1 Multi-Valued Neuron
The discrete multi-valued neuron (MVN) was
proposed in (Aizenberg N. and Aizenberg I., 1992)
as a neural element based on the principles of
multiple-valued threshold logic over the field of
complex numbers. These principles have been
formulated in (Aizenberg N. and Ivaskiv, 1977) and
then developed and deeply considered in (Aizenberg
I. et al., 2000). A discrete-valued MVN performs a
mapping between n inputs and a single output. This
mapping is described by a multiple-valued (k-
valued) function of n variables
)(
1 n
x ..., ,xf
and it
can be represented using n+1 complex-valued
weights as follows:
)()(
1101 nnn
xw...xwwPx ..., ,xf ++
+
=
,
(1)
where
n
x ..., ,x
1
are the variables, on which the
performed function depends, and
n
, ...,w,ww
10
are the weights. The values of the function and of
the variables are complex. They are the k
th
roots of
unity:
)2exp( j/ki
j
π=ε ,
{0 1,..., 1}j,k-∈
, i is
IJCCI 2009 - International Joint Conference on Computational Intelligence
348

an imaginary unity. P is the activation function of
the neuron:
() exp(2 )
if 2 arg 2 ( 1) ,
Pz= i j/k,
j/k z j+ /k
π
ππ
≤<
(2)
where j=0, 1, ..., k-1 are values of the k-valued logic,
nn
xw...xwwz +++=
110
is the weighted sum ,
arg z is the argument of the complex number z.
(
)
() exp 2 /Pz ji k
π
=⋅
Figure 1: Geometrical interpretation of the discrete-valued
MVN activation function.
Equation (2) is illustrated in Figure 1 Function (2)
divides the complex plane into k equal sectors and
maps the whole complex plane onto a subset of
points belonging to the unit circle. This subset is
exactly a set of the k
th
roots of unity.
The MVN learning is reduced to the movement
along the unit circle. It is derivative-free. The
shortest way of this movement is completely
determined by the error, which is a difference
between the desired and actual outputs. The error-
correction learning rule and the corresponding
learning algorithm for the discrete-valued MVN
were described in detail in (Aizenberg I. et al., 2000)
and recently modified by Aizenberg I and Moraga,
(2007):
()
()
1
1
rr qs
r
r
C
WW X
nz
εε
+
=+ −
+
(3)
where
X
is the input vector with the components
complex-conjugated, n is the number of neuron
inputs,
q
ε
is the desired output of the neuron,
()
s
P
z
ε
=
is the actual output of the neuron (see
Figure 2), r is the number of the learning iteration,
r
W is the current weighting vector (to be
corrected),
1r
W
+
is the following weighting vector
(after correction), C
r
is the constant part of the
learning rate (it may always be equal to 1), and
r
z
is the absolute value of the weighted sum obtained
on the r
th
iteration. A factor 1/
r
z is a variable part
of the learning rate. The use of it can be important
for learning highly nonlinear functions with a
number of high irregular jumps. However, it should
not be used for learning smooth, non-spiky
functions. Rule (3) ensures such a correction of the
weights that the weighted sum moves from sector s
to sector q (see Figure 2). The direction of this
movement is determined by the error
qs
δ
εε
=−.
The convergence of this learning algorithm is proven
in (Aizenberg I. et al., 2000).
Figure 2. Geometrical interpretation of the MVN learning
rule.
2.2 Universal Binary Neuron
The universal binary neuron (UBN) was introduced
in (Aizenberg I., 1991) and then developed and
considered in detail in (Aizenberg I. et al., 2000). In
(Aizenberg I., 2008), a new learning algorithm was
proposed for the UBN.
A key idea behind the UBN is the use of
complex-valued weights and an original activation
function for learning nonlinearly separable Boolean
functions. A classical threshold activation function
(sign) separates a real domain into two parts
()
1, 0
sign
1, 0.
z
z
z
≥
⎧
=
⎨
−
<
⎩
If k=2 in (2) then activation function (2)
separates the complex domain into two parts as well
(the complex plain is separated into the top
semiplane (“1”) and the bottom semiplane (“-1”):
i
0
1
k-2
Z
J-
J
J+1
k-1
s
ε
q
ε
A MULTI-VALUED NEURON WITH A PERIODIC ACTIVATION FUNCTION
349

()
1, 0 arg( )
1, arg( ) 2 .
z
Pz
z
π
π
π
≤<
⎧
=
⎨
−≤ <
⎩
However, this activation function does not
increase the neuron’s functionality: although the
weights are complex, the neuron still can only learn
linearly separable functions. In (Aizenberg I., 1991),
it was suggested to use an l-multiple activation
function
() (1)
if 2 arg( ) 2 ( 1)
2,
j
B
Pz= ,
j/m z j+ /m,
m= l, l
ππ
−
≤<
∈N
(4)
where l is some positive integer, j is a non-negative
integer
mj <0 ≤
.
Figure 3: Definition of the function (4).
Activation function (4) is illustrated in Figure 3.
Function (4) separates the complex plane into m =2l
equal sectors. It determines the neuron’s output by
the alternating sequence of 1, -1, 1, -1,… depending
on the parity of the sector’s number. It equals to 1
for the complex numbers from the even sectors 0, 2,
4, ..., m-2 and to -1 for the numbers from the odd
sectors 1, 3, 5, ..., m-1.
As it was shown in (Aizenberg I., 1991) and,
(Aizenberg I. et al., 2000), any non-threshold
Boolean function (of course, including XOR and
parity n) may be learned by a single UBN with
activation function (4), and no network is needed to
learn them.
The question is: will a similar modification of
activation function (2) lead to an increase in the
MVN’s functionality?
3 MULTIPLE L-REPETITIVE
MVN’S DISCRETE
ACTIVATION FUNCTION
Let
{
}
21
1, , ,...,
k
kkkk
E
εε ε
−
= (where
2/ik
k
e
π
ε
=
is the primitive k
th
root of unity) be the set of the k
th
roots of unity. Let O be the continuous set of the
points located on the unit circle. Let
{
}
0,1,..., 1Kk
=
− be the set of the values of k-
valued logic. Let
)(
1 n
x ..., ,xf
be a function and
either
:
n
k
f
EK→
or :
n
f
OK→ . Hence, the
range of
f is discrete, while its domain is either
discrete or continuous. In general, its domain may be
even hybrid. If some function
1
( ), , , , , 1,...,
n i jj jj
f
y , ..., y y a b a b j n
⎡⎡
∈∈=
⎣⎣
R
is defined on the bounded subdomain
nn
D ⊂ R
(
:
n
f
DK→
), then it can be easily transformed to
:
n
f
OK→
by a simple linear transformation
applied to each variable:
[[
,
2 0, 2 , 1, 2,..., ,
jjj
jj
j
jj
yab
ya
j
n
ba
ϕππ
⎡⎡
∈⇒
⎣⎣
−
⇒= ∈ =
−
and then
, 1, 2,...,
j
i
j
x
eOj n
ϕ
=∈ = is the
complex number located on the unit circle. Hence,
we obtain the function
1
( ):
n
n
f
x , ..., x O K→
.
If this function
)(
1 n
x ..., ,xf
is not a k-valued
threshold function, it can not be learned by a single
MVN with the activation function (2).
Let us “immerse” the k-valued function
)(
1 n
x ..., ,xf
into an m-valued logic, where mkl
=
,
l is integer and
2l ≥
. To do this, let us define the
following new discrete activation function for the
MVN:
() mod
if 2 arg 2 ( 1) ,
0,1,..., 1; , 2.
l
Pz=j k,
j/m z j+ /m
jmmkll
ππ
≤<
=−=≥
(5)
This definition is illustrated in Figure 4. Activation
function (5) separates the complex plane onto
m
IJCCI 2009 - International Joint Conference on Computational Intelligence
350
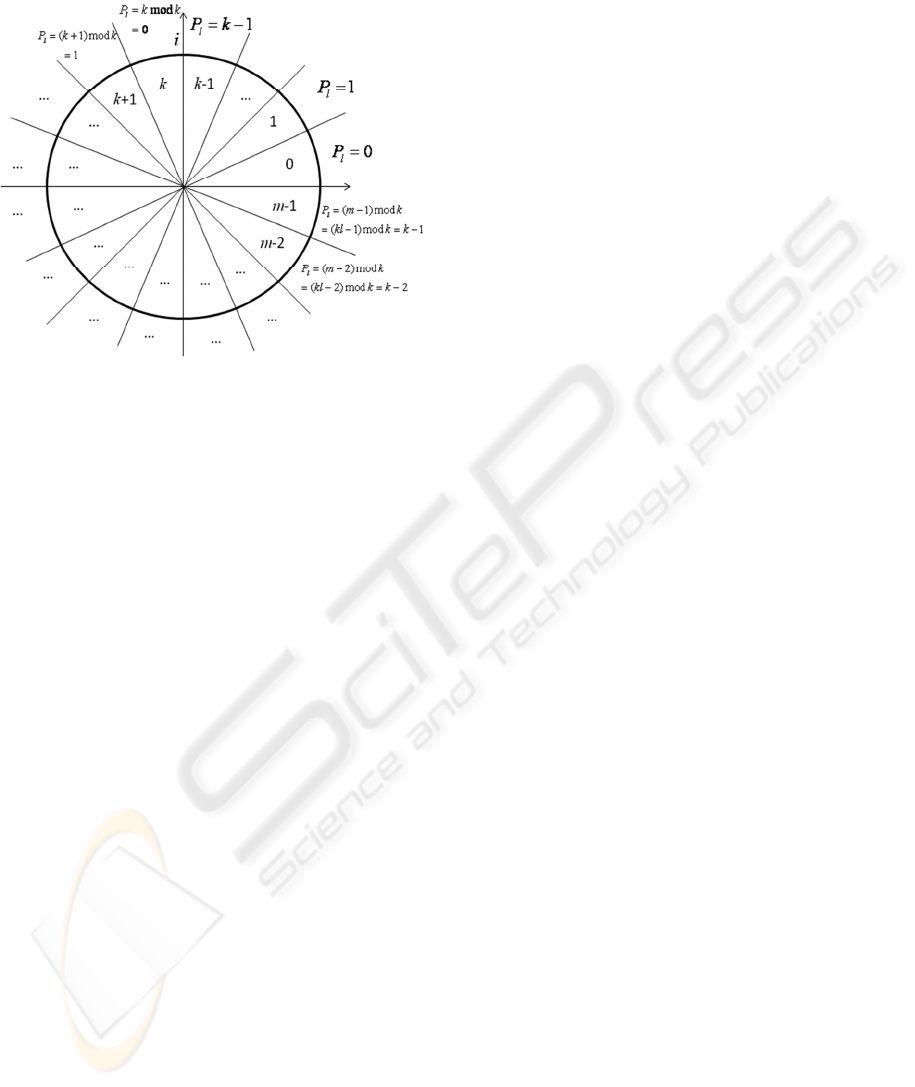
equal sectors and
tK∀∈ there are exactly l
sectors, where (5) equals to
t.
Figure 4: Geometrical interpretation of the l-repeated
multiple discrete-valued MVN activation function (5).
This means that activation function (5) establishes
mappings from
k
E into
{
}
21
1, , ,...,
k
mmmm
E
εε ε
−
=
and from
K into
{
}
0,1,..., 1, , 1,..., 1Mkkkm=−+−
, respectively.
Since
mkl= then each element from M and
m
E
has exactly
l prototypes in K and
k
E , respectively.
In turn, this means that the MVN’s output,
depending in which one of the m sectors (whose
ordinal numbers are determined by the elements of
the set M) the weighted sum is located, is equal to
01 1
0,1,..., 1, 0,1,..., 1,..., 0,1,..., 1.
l
lk m
kk k
−
=
−− −
(6)
Hence the MVN’s activation function in this case
becomes k-periodic and l-multiple.
On the other hand, activation function (5)
“immerses” a k-valued function
)(
1 n
x ..., ,xf
into
m-valued logic. This immersing will have a great
sense, if
)(
1 n
x ..., ,xf
, being a non-threshold
function in k-valued logic, will be a threshold
function in m-valued logic and therefore it will be
possible to learn it using a single MVN. It will be
shown below that this is definitely the case.
It is important to mention that if
1l =
in (5) then
m=k and activation function (5) coincides with
activation function (2) accurate within the
interpretation of the neuron’s output (if the weighted
sum is located in the j
th
sector then according to (2)
the neuron’s output is equal to
2/ij k j
k
eE
π
ε
=∈
,
which is the j
th
k
th
root of unity, while in (5) it is
equal to
j
K
∈
).
4 LEARNING ALGORITHM FOR
THE MVN WITH MULTIPLE
L-REPETITIVE ACTIVATION
FUNCTION
To make the approach proposed in Section 3 active,
it is necessary to develop an efficient learning
algorithm for the MVN with activation function (5).
Such an algorithm will be presented here.
As it was mentioned above (Section 2), one of
the MVN learning algorithms is based on error-
correction learning rule (3). Let us adapt this
algorithm to activation function (5).
Let
)(
1 n
x ..., ,xf
be a function of k-valued logic
and
:
n
k
f
EK→
or
:
n
f
OK→
. Let this function
be non-learnable using a single MVN with activation
function (2). Let us try to learn it in m-valued logic
using a single MVN with activation function (5).
Thus, the expected result of this learning process is
the representation of
)(
1 n
x ..., ,xf
according to (1),
where the activation function
l
P determined by (5)
substitutes for
the activation function P determined
by (2).
This learning process may be based on the same
learning rule (3), but applied to
)(
1 n
x ..., ,xf
as to
the m-valued function. To use learning rule (3), it is
necessary to determine a desired output. Unlike the
case of the MVN with activation function (2), a
desired output in terms of m-valued logic cannot be
determined unambiguously for the MVN with
activation function (5). According to (5), there are
exactly
l sectors on the complex plane out of m,
where this activation function equals to the given
desired output
tK
∈
. Therefore, there are exactly l
m
th
roots of unity that can be used as the desired
outputs in rule (3). Which one of them should we
choose? We suggest using the same approach that
was used in the error-correction learning algorithm
for the UBN (Aizenberg I. et al., 2000). UBN’s
activation function (4) determines an alterning
sequence with respect to sectors on the complex
plane. Hence, if the actual output of the UBN is not
A MULTI-VALUED NEURON WITH A PERIODIC ACTIVATION FUNCTION
351

correct, in order to make the correction, we can
“move” the weighted sum into either of the sectors
adjacent to the one where the current weighted sum
is located. It was suggested to always move it to the
sector, which is closest to the current weighted sum
(in terms of the angular distance). The convergence
of this learning algorithm was proven in (Aizenberg
I. et al., 2000).
Let us use the same approach here. Activation
function (5) determines l-multiple and k-periodic
sequence (6) with respect to sectors on the complex
plane. Suppose that the current MVN’s output is not
correct and the current weighted sum is located in
the sector
{
}
0,1,..., 1sM m∈= −
. Since
2l ≥
in
(5), there are
l sectors on the complex plane, where
function (5) takes the correct value. Two of these
l
sectors are the closest ones to sector
s (from right
and left sides, respectively). From these two sectors,
we choose sector
q whose border is closest to the
current weighted sum
z. Then learning rule (3) can
be applied. Hence, the learning algorithm for the
MVN with activation function (5) may be described
as follows. Let us have
N learning samples for the
function
)(
1 n
x ..., ,xf
to be learned and
{
}
1,...,
j
N∈ be the number of the current learning
sample (initially,
1
j
=
). One iteration of the
learning process consists of the following steps:
1) Check (1) with activation
function (5) for the learning sample j.
2) If (1) holds then set
1
j
j=+
.
3) If
jN≤
then go to step 1,
otherwise go to step 7.
3) Let z be the current value of the
weighted sum and
(
)
,
s
Pz s M
ε
=∈. Find
1
qM∈ , which determines the closest
sector to the s
th
one, where the output
is correct, from the right, and find
2
qM∈ , which determines the closest
sector to the s
th
one, where the output
is correct, from the left.
4) If
()
()
()
()
1
2
(1)2/
2/
arg arg mod 2
arg arg mod 2
iq m
iq m
ze
ez
π
π
π
π
+
−≤
≤−
then
1
qq=
else
2
qq
=
.
5) Apply learning rule (3) to adjust
the weights.
6) Set
1jj=+
and return to step 1.
7) End.
Since according to this learning algorithm the
learning of a k-valued function is reduced to the
learning of a partially defined m-valued function, the
convergence of the learning algorithm may be
proven in the same manner as the convergence of the
learning algorithm based on rule (3) and of the UBN
learning algorithm were proven in (Aizenberg I. et
al., 2000).
5 SIMULATIONS
To confirm the efficiency of the proposed activation
function and learning algorithm, they were checked
for the following three problems using a software
simulator written in Borland Delphi 5.0 running on a
PC with the Intel® Core™2 Duo CPU.
5.1 Wisconsin Breast Cancer
(Diagnostic)
This famous benchmark database was downloaded
from the UC Irvine Machine Learning Repository
(Asuncion and Newman, 2007). It contains 569
samples that are described by 30 real-valued
features. There are two classes (“malignant” and
“benign”) to which these samples belong.
A single MVN with activation function (2) with
2k
=
fails to learn the entire data set even after
1,000,000 iterations. However, a single MVN with
activation function (5) with
2, 2, 4klm== =
learns the problem with no errors. Ten runs of the
learning process started from different random
weights resulted in convergence after 649-1300
iterations, which took a few seconds.
We have also tested the ability of a single MVN
to solve classification problem. 10-fold cross
validation was used as it is recommended in
(Asuncion and Newman, 2007). Every time the data
set was divided into a learning set (400 samples) and
a testing set (169) samples. After the learning set
was learned completely with no errors, the
classification of the testing set samples was
performed. A classification rate of 96.5%-97.5%
was achieved. This is comparative to the best known
result (97.5%) (Asuncion and Newman, 2007).
However, it is important to note that our method
solves the problem using just a single neuron, while
in the previous works either different networks or
linear programming methods were used.
IJCCI 2009 - International Joint Conference on Computational Intelligence
352

5.2 Sonar
This famous benchmark database was also
downloaded from the UC Irvine Machine Learning
Repository (Asuncion and Newman, 2007). It
contains 208 samples that are described by 60 real-
valued features. There are two classes (“mine” and
“rock”) to which these samples belong.
A single MVN with activation function (2) with
2k =
fails to learn the entire data set even after
1,000,000 iterations. However, the single MVN with
activation function (5) with
2, 2, 4klm== =
learns the problem with no errors. Ten runs of the
learning process started from different random
weights resulted in convergence after 65-180
iterations, which took a few seconds.
We have also tested the ability of a single MVN
to solve the classification problem. This set is
initially divided by its creators into learning (104
samples) and testing (104 samples) subsets. After
the learning set was learned completely with no
errors, the classification of the testing set samples
was performed. The classification rate of 88.1%-
91.5% was achieved. This is comparative to the best
known results reported in (Chen J.-H. and Chen C.-
S., 2002) – 94% (Fuzzy Kernel Perceptron), 89.5%
(SVM), and in (Aizenberg I. and Moraga, 2007) -
88%-93% (MLMVN). However, here the problem
was solved using just a single neuron, while in the
previous works different neural and kernel-based
networks were used.
5.3 k-Valued Non-threshold Function
Let us consider the following fully defined function
of 3 variables of 4-valued logic
()( )
123 1 2 3
,, mod4fxxx x x x=++
(see the first
four columns of Table 1). This function, which is the
analogue of parity 3 function in the Boolean logic, is
non-threshold in 4-valued logic and can not be
learned using a single MVN with activation function
(2) with
4k = . However, this function can be
learned by a single MVN with activation function
(5) with
4, 8, 16klm== =
(see columns 5-6 of
Table 1). The learning process converges after 584-
43875 iterations (ten independent runs).
It is interesting that every time the learning process
has converged to different weighting vectors, but to
the same type of a resulting monotonic m-valued
function (see the 5
th
column of the Table 1). This
confirms that the learning of a non-threshold k-
valued function may be reduced to the learning of a
partially defined m-valued threshold function.
Table 1: Non-threshold function of 3 variables of 4-valued
logic and the results of its learning.
1
x
2
x
3
x
(
)
123
,,
f
xx x
4-valued
j
M∈
,
{
}
0,1,...,15M =
mod 4
l
P
j
=
=
0 0 0 0 8 0
0 0 1 1 9 1
0 0 2 2 10 2
0 0 3 3 11 3
0 1 0 1 9 1
0 1 1 2 10 2
0 1 2 3 11 3
0 1 3 0 12 0
0 2 0 2 10 2
0 2 1 3 11 3
0 2 2 0 12 0
0 2 3 1 13 1
0 3 0 3 11 3
0 3 1 0 12 0
0 3 2 1 13 1
0 3 3 2 14 2
1 0 0 1 9 1
1 0 1 2 10 2
1 0 2 3 11 3
1 0 3 0 12 0
1 1 0 2 10 2
1 1 1 3 11 3
1 1 2 0 12 0
1 1 3 1 13 1
1 2 0 3 11 3
1 2 1 0 12 0
1 2 2 1 13 1
1 2 3 2 14 2
1 3 0 0 12 0
1 3 1 1 13 1
1 3 2 2 14 2
1 3 3 3 15 3
2 0 0 2 10 2
2 0 1 3 11 3
2 0 2 0 12 0
2 0 3 1 13 1
2 1 0 3 11 3
2 1 1 0 12 0
2 1 2 1 13 1
2 1 3 2 14 2
2 2 0 0 12 0
2 2 1 1 13 1
2 2 2 2 14 2
2 2 3 3 15 3
2 3 0 1 13 1
2 3 1 2 14 2
2 3 2 3 15 3
2 3 3 0 16 0
3 0 0 3 11 3
3 0 1 0 12 0
3 0 2 1 13 1
3 0 3 2 14 2
3 1 0 0 12 0
3 1 1 1 13 1
3 1 2 2 14 2
3 1 3 3 15 3
3 2 0 1 13 1
3 2 1 2 14 2
3 2 2 3 15 3
3 2 3 0 16 0
3 3 0 2 14 2
3 3 1 3 15 3
3 3 2 0 16 0
3 3 3 1 17 1
A MULTI-VALUED NEURON WITH A PERIODIC ACTIVATION FUNCTION
353

6 CONCLUSIONS
We have presented here a new activation function
for a multi-valued neuron. This l- multiple activation
function makes it possible to learn nonlinearly
separable problems and non-threshold multiple-
valued functions using a single multi-valued neuron.
This significantly increases the MVN’s functionality
and makes the MVN more efficient in applications.
The learning algorithm for the MVN with the l-
multiple activation function was also presented.
ACKNOWLEDGEMENTS
The author appreciates the assistance of the UC
Irvine machine Learning Repository (Asuncion and
Newman, 2007), from where two data sets were
downloaded for the simulation purposes.
REFERENCES
Aizenberg, N.N and Aizenberg, I.N. (1992). CNN Based
on Multi-Valued Neuron as a Model of Associative
Memory for Gray-Scale Images, In Proceedings of the
Second IEEE Int. Workshop on Cellular Neural
Networks and their Applications, Technical University
Munich, 36-41
Aizenberg, N.N. Ivaskiv, Yu. L., and Pospelov, D.A.
(1971). About one Generalization of the Threshold
Function Doklady Akademii Nauk SSSR (The Reports
of the Academy of Sciences of the USSR), 196, 1287-
1290, (in Russian).
Aizenberg, N.N. and Ivaskiv, Yu.L. (1977). Multiple-
Valued Threshold Logic. Naukova Dumka Publisher
House, Kiev (in Russian).
Aizenberg. I.N. (1991). The Universal Logical Element
over the Field of the Complex Numbers, Kibernetika
(Cybernetics and Systems Analysis) 27,, 116-121 (in
Russian, journal is translated into English by
Consultants Bureau, An Imprint of Springer Verlag
New York LLC, Vol. 27, 467-473).
Aizenberg, I., Aizenberg, N., and Vandewalle, J. (2000).
Multi-valued and universal binary neurons: theory,
learning, applications. Kluwer Academic Publishers,
Boston Dordrecht London.
Aizenberg, I. and Butakoff, C. (2002). Image Processing
Using Cellular Neural Networks Based on Multi-
Valued and Universal Binary Neurons, Journal of
VLSI Signal Processing Systems for Signal, Image and
Video Technology, 32, 169-188.
Aizenberg, I., Moraga, C., and Paliy D. (2005). A
Feedforward Neural Network based on Multi-Valued
Neurons, In Computational Intelligence, Theory and
Applications. Advances in Soft Computing, XIV, (B.
Reusch - Ed.), Springer, Berlin, Heidelberg, New
York, 599-612.
Aizenberg, I. and Moraga, C. (2007). Multilayer
Feedforward Neural Network Based on Multi-Valued
Neurons (MLMVN) and a Backpropagation Learning
Algorithm", Soft Computing, 11, 169-183.
Aizenberg, I., Paliy, D. V., Zurada, J.M., and Astola J. T.
(2008). Blur Identification by Multilayer Neural
Network based on Multi-Valued Neurons, IEEE
Transactions on Neural Networks, 19, 883-898.
Aizenberg, I. (2008). Solving the XOR and Parity n
Problems Using a Single Universal Binary Neuron,
Soft Computing, 12, 215-222.
Asuncion, A. and Newman, D.J. (2007). UCI Machine
Learning Repository
[http://www.ics.uci.edu/~mlearn/MLRepository.html].
Irvine, CA: University of California, School of
Information and Computer Science.
Aoki, H. and Kosugi, Y. (2000). An Image Storage
System Using Complex-Valued Associative Memory,
In Proceedings. of the 15
th
International Conference
on Pattern Recognition. 2, 626-629.
Aoki, H., Watanabe, E., Nagata, A., and Kosugi Y. (2001).
Rotation-Invariant Image Association for Endoscopic
Positional Identification Using Complex-Valued
Associative Memories. In Bio-inspired Applications of
Connectionism, Lecture Notes in Computer Science
(Mira J., Prieto A. -eds) Springer, Berlin Heidelberg
New York, 2085, 369-374.
Chen, J.-H and Chen, C.-S. (2002). Fuzzy Kernel
Perceptron. IEEE Transactions on Neural Networks
13, 1364-1373.
Jankowski, S., Lozowski, A., and Zurada J.M. (1996).
Complex-Valued Multistate Neural Associative
Memory. IEEE Tranactions. on Neural Networks 7,
1491-1496.
Lee, D.L. (2001). Improving the Capacity of Complex-
Valued Neural Networks with a Modified Gradient
Descent Learning Rule IEEE Transactions on Neural
Networks 12, 439–443.
Lee, D.L. (2004). "Complex-valued Neural Associative
Memories: Learning Algorithm and Network
Stability", in book "Complex-Valued Neural
Networks: Theories and Applications" (Hirose A.–
Ed.), World Scientific, 29-56.
Muezzinoglu, M. K., Guzelis, C., and Zurada J. M, (2003).
A New Design Method for the Complex-Valued
Multistate Hopfield Associative Memory, IEEE
Transactions on Neural Networks 14, 891-899.
IJCCI 2009 - International Joint Conference on Computational Intelligence
354
