EVOLUTIONARY PROGRAMMING GUIDED BY ANALYTICALLY

GENERATED SEEDS

Neil Crossley, Emanuel Kitzelmann, Martin Hofmann and Ute Schmid

Faculty Information Systems and Applied Computer Science, University of Bamberg, 96045 Bamberg, Germany

Keywords:

Recursive functions, Analytical inductive programming, Evolutionary programming.

Abstract:

Evolutionary programming is the most powerful method for inducing recursive functional programs from in-

put/output examples while taking into account efﬁciency and complexity constraints for the target program.

However, synthesis time can be considerably high. A strategy which is complementary to the generate-and

-test based approaches of evolutionary programming is inductive analytical programming where program con-

struction is example-driven, that is, target programs are constructed as minimal generalization over the given

input/output examples. Synthesis with analytical approaches is fast, but the scope of synthesizable programs is

restricted. We propose to combine both approaches in such a way that the power of evolutionary programming

is preserved and synthesis becomes more efﬁcient. We use the analytical system IGOR2 to generate seeds in

form of program skeletons to guide the evolutionary system ADATE when searching for target programs. In

an evaluations with several examples we can show that using such seeds indeed can speed up evolutionary

programming considerably.

1 INTRODUCTION

Inductive programming research is concerned with

the synthesis of recursive programs from incomplete

speciﬁcations. Target programs are typically declara-

tive – mostly functional (Kitzelmann, 2009; Olsson,

1995), sometimes logical (Quinlan and Cameron-

Jones, 1995; Flener and Yilmaz, 1999). Speciﬁca-

tions are typically given in the form of input/output

examples for the desired behavior of the target pro-

gram. In addition, constraints for code complexity or

time efﬁciency can be provided. There are two dis-

tinct approaches to inductive programming: analyti-

cal and evolutionary inductive programming.

Analytical inductive programming is data-driven

and often relies on speciﬁcations which consist only

of a small set of positive input/output examples. A

recursive program is learned by detecting recurrence

relations in the input/output examples and generaliza-

tion over these regularities (Summers, 1977; Kitzel-

mann and Schmid, 2006). Typically, analytical ap-

proaches are fast and they can guarantee certain char-

acteristics for the constructed program such as mini-

mality of the generalization with respect to the given

examples and termination. However, the class of

learnable programs is necessarily restricted to such

problems which can be speciﬁed by small sets of

input/output examples. The scope of learnable pro-

grams can be somewhat widened by allowing the use

of background knowledge (Kitzelmann, 2009).

Evolutionary inductive programming is based on

search through the hypothesis space of possible pro-

grams given some programming language. A hy-

pothesis is returned as a solution if it performs sufﬁ-

ciently well on the input/output examples with respect

to some measure of ﬁtness, typically involving code

length and time efﬁciency. In that sense, evolutionary

programming is a speciﬁc variant of generate and test.

The scope of programs learnable with an evolutionary

approach is, in principle, unrestricted. But, genera-

tion times are typically high and there is no guarantee

that the returned program is the optimal solution with

respect to the ﬁtness function.

Therefore, we propose to use analytical induc-

tive programming to generate initial seeds for evolu-

tionary programming. The combination of both ap-

proaches should be such that if a solution can be gen-

erated by analytical means alone, this fast and reliable

approach should be used exclusively. If the problem

is out of scope for analytical programming, at least

a partial solution could be provided which then can

be used as input for program evolution. Based on

some initial experiments (Crossley et al., 2009), we

will present more extensive analyses in this paper.

198

Crossley N., Kitzelmann E., Hofmann M. and Schmid U. (2009).

EVOLUTIONARY PROGRAMMING GUIDED BY ANALYTICALLY GENERATED SEEDS.

In Proceedings of the International Joint Conference on Computational Intelligence, pages 197-202

DOI: 10.5220/0002286301970202

 SciTePress

In the following, we ﬁrst describe the evolutionary

programming system ADATE and the analytical pro-

gramming system IGOR2 (Kitzelmann, 2009). After-

wards we will introduce different strategies for the an-

alytical generation of program seeds with IGOR2 and

their incorporation in ADATE. We will report results

of our ﬁrst experiments and give a short conclusion.

2 ADATE

ADATE (Olsson, 1995; Vattekar, 2006) was initially

proposed in the nineties and has been continually ex-

tended. To our knowledge, it is the most powerful ap-

proach to inductive programming which is currently

available. ADATE constructs programs in a subset of

the functional language ML, called ADATE-ML. The

problem speciﬁcation presented to ADATE consists

of: a set of data types and a set of primitive functions;

a set of sample inputs; an evaluation function; an ini-

tial declaration of the goal function f . Sample inputs

typically are input/output pairs. It is enough to give

only positive examples, but it is additionally possible

to provide negative examples. There are a number of

predeﬁned evaluation functions, each using different

measures for syntactic complexity and time efﬁciency

of the goal program. These are completed by a call-

back evaluation function given in the problem speciﬁ-

cation which evaluates the return value of an inferred

function for a given input example. In general, the

search heuristic is to prefer smaller and faster func-

tions. As is typical for evolutionary approaches, there

are sets of individuals which are developed over gen-

erations such that ﬁtter individuals have more chances

to reproduce. If no additional knowledge is provided,

in contrast to usual approaches, ADATE starts with a

single individual – the empty function f .

The function declarations of all constructed pro-

gram candidates use the declaration of f , differing

only in the program body. To construct program

bodies, only the programming constructs available in

ADATE-ML can be used together with additionally

data types and primitive functions provided in the

problem speciﬁcation.

The search operators are transformations used in

reproduction to generate new individuals. These

transformations include: replacements of expressions

in the program body, abstraction of expressions by

introducing a call to a newly introduced function,

distributing a function call currently outside a case

expression over all cases, and altering the number

and type of function arguments by various embed-

ding techniques. From these ADATE constructs com-

pound transformations, consisting of multiple atomic

transformations, depending on the current stage of the

search. Through management of an upper bound for

the number of compound transformations used to gen-

erate individuals, ADATE can employ iterative deep-

ening in its exploration of the problem space. In the

current version of ADATE crossover is realized by ap-

plying a compound transformation from one individ-

ual to another (Vattekar, 2006).

In our experiments we used ADATE with the same

set of only positive input/output examples which can

be presented to the analytical system IGOR2. No

data types and function primitives beyond ADATE-

ML were used. Performance was evaluated with the

predeﬁned measures. Correctness was evaluated by a

user-deﬁned all-or-nothing function. The searched-

for program f was presented either with an empty

body or with an initial seed constructed by analytical

induction. A simple example is given in ﬁgure 1.

With only the minimum necessary background

knowledge, such as necessary data types and atomic

functions, ADATE is able to ﬁnd reasonable solutions

given enough time. Additional background knowl-

edge can reduce the required transformations to in-

fer correct solutions, which can also reduce search

time. However, additional background knowledge ex-

acts deeper insights into the problem on behalf of the

problem speciﬁer. From a programming assistance

system perspective, it would be not convenient to ex-

pect that a human programmer could provide exactly

such knowledge which would increase the speed of

generating a solution. This would presuppose (a) that

the user understands the inner workings of ADATE

and (b) has a deep insight in the programming prob-

lem at hand. From a cognitive perspective, such addi-

tional knowledge to guide ADATE’s search might be

gained by a closer inspection of the structure of the in-

put/output examples, thereby providing ADATE with

a helpful initial hypothesis.

3 IGOR2

IGOR2 (Kitzelmann, 2009) – to our knowledge – is

currently the most powerful system for analytical in-

ductive programming. Its scope of inducable pro-

grams and the time efﬁciency of the induction algo-

rithm compares very well with classical approaches

to inductive logic programming and other approaches

to inductive programming (Hofmann et al., 2008).

IGOR2 continues the tradition of previous work in

learning LISP functions from examples (Summers,

1977) as the successor to IGOR1 (Kitzelmann and

Schmid, 2006).

The system is realized in the constructor term

EVOLUTIONARY PROGRAMMING GUIDED BY ANALYTICALLY GENERATED SEEDS

199

Examples (represented in MAUDE notation):

sorts elem list.

ops a b c d: -> elem list [ctor].

op nil: -> list [ctor].

op _,_ : elem list -> list [ctor].

eq swap(nil) = nil.

eq swap((a,nil)) = (a,nil).

eq swap((a, b, nil)) = (b, a, nil).

swap((a, b, c, nil)) = (c, b, a, nil).

swap((a, b, c, d, nil)) = (d, b, c, a, nil).

Program induced by IGOR2:

1. swap( nil ) = nil.

2. swap( (X, XS) ) = (last((X,XS)), sub((X,XS))).

3. last( (X, nil) ) = X.

4. last( (X, XS) ) = last(XS).

5. sub ( (X, nil) ) = nil.

6. sub ( (X,Y,XS) ) = swap((X , sub((Y,XS)))).

Best program induced by ADATE with empty seed:

fun f Xs =

case Xs of

nill => Xs

| cons( V144C, V144D) =>

case V144D of

nill => Xs

| cons( V63EC5, V63EC6 ) =>

case f( V63EC6 ) of

nill => cons( V63EC5, cons( V144C, V63EC6 ) )

| cons( V66B8B, V66B8C ) =>

cons( V66B8B, cons( V63EC5, f( cons( V144C, V66B8C ) ) ) )

Figure 1: The Swap Function.

rewriting system MAUDE. Therefore, all constructors

speciﬁed for the data types used in the given exam-

ples are available for program construction. IGOR2

speciﬁcations consist of: a small set of positive in-

put/output examples, presented as equations, which

have to be the ﬁrst examples with respect to the un-

derlying data type and a speciﬁcation of the input data

type. Furthermore, background knowledge for addi-

tional functions can (but must not) be provided.

IGOR2 can induce several dependent target func-

tions (i.e., mutual recursion) in one run. Auxiliary

functions are invented if needed. In general, a set of

rules is constructed by generalization of the input data

by introducing patterns and predicates to partition the

given examples and synthesis of expressions comput-

ing the speciﬁed outputs. Partitioning and search-

ing for expressions is done systematically and com-

pletely which is tractable even for relatively complex

examples because construction of hypotheses is data-

driven. An example of a problem speciﬁcation and a

solution produced by IGOR2 is given in ﬁgure 1.

Considering hypotheses as equations and apply-

ing equational logic, the analytical method assures

that only hypotheses entailing the provided example

equations are generated. However, the intermediate

hypotheses may be unﬁnished in that the rules contain

unbound variables in the right-hand side (rhs), i.e., do

not represent functions. The search stops, if one of the

currently best hypotheses is ﬁnished, i.e., all variables

in the rhss are bound.

IGOR2’s built-in inductive bias is to prefer fewer

case distinctions, most speciﬁc patterns and fewer re-

cursive calls. Thus, the initial hypothesis is a sin-

gle rule per target function which is the least gen-

eral generalization of the example equations. If a rule

contains unbound variables, successor hypotheses are

computed using the following operations: (i) Parti-

tioning of the inputs by replacing one pattern by a

set of disjoint more speciﬁc patterns or by introduc-

ing a predicate to the righthand side of the rule; (ii)

replacing the righthand side of a rule by a (recursive)

call to a deﬁned function (including the target func-

tion) where ﬁnding the argument of the function call

is treated as a new induction problem, that is, an aux-

iliary function is invented; (iii) replacing subterms in

the righthand side of a rule which contain unbound

variables by a call to new subprograms.

Reﬁning a Pattern. Computing a set of more spe-

ciﬁc patterns, case (i), in order to introduce a case

distinction, is done as follows: A position in the pat-

tern p with a variable resulting from generalising the

corresponding subterms in the subsumed example in-

puts is identiﬁed. This implies that at least two of the

subsumed inputs have different constructor symbols

at this position. Now all subsumed inputs are parti-

tioned such that all of them with the same constructor

at this position belong to the same subset. Together

with the corresponding example outputs this yields a

partition of the example equations whose inputs are

subsumed by p. Now for each subset a new initial hy-

pothesis is computed, leading to one set of successor

rules. Since more than one position may be selected,

different partitions may be induced, leading to a set of

successor rule-sets.

For example, let

reverse([]) = []

reverse([X]) = [X]

reverse([X, Y ]) = [Y, X]

be some examples for the reverse-function. The pat-

tern of the initial rule is simply a variable Q, since

the example input terms have no common root sym-

bol. Hence, the unique position at which the pattern

contains a variable and the example inputs different

constructors is the root position. The ﬁrst example in-

put consists of only the constant [] at the root position.

All remaining example inputs have the list constructor

cons as root. Put differently, two subsets are induced

by the root position, one containing the ﬁrst example,

the other containing the two remaining examples. The

least general generalizations of the example inputs of

IJCCI 2009 - International Joint Conference on Computational Intelligence

200

these two subsets are [] and [Q|Qs] resp. which are the

(more speciﬁc) patterns of the two successor rules.

Introducing (Recursive) Function Calls and Aux-

iliary Functions. In cases (ii) and (iii) help func-

tions are invented. This includes the generation of

I/O-examples from which they are induced. For case

(ii) this is done as follows: Function calls are intro-

duced by matching the currently considered outputs,

i.e., those outputs whose inputs match the pattern of

the currently considered rule, with the outputs of any

deﬁned function. If all current outputs match, then

the rhs of the current unﬁnished rule can be set to a

call of the matched deﬁned function. The argument

of the call must map the currently considered inputs

to the inputs of the matched deﬁned function. For case

(iii), the example inputs of the new deﬁned function

also equal the currently considered inputs. The out-

puts are the corresponding subterms of the currently

considered outputs.

For an example of case (iii) consider the last two

reverse examples as they have been put into one sub-

set in the previous section. The initial rule for these

two examples is:

reverse([Q|Qs]) = [Q2|Qs2] (1)

This rule is unﬁnished due to the two unbound vari-

ables in the rhs. Now the two unﬁnished subterms

(consisting of exactly the two variables) are taken as

new subproblems. This leads to two new examples

sets for two new help functions sub1 and sub2:

sub1([X]) = X sub2([X]) = []

sub1([X, Y ]) = Y sub2([X, Y ]) = [X]

The successor rule-set for the unﬁnished rule contains

three rules determined as follows: The original unﬁn-

ished rule (1) is replaced by the ﬁnished rule:

reverse([Q|Qs]) = [sub1([Q|Qs] | sub2[Q|Qs]]

And from both new example sets an initial rule is de-

rived.

Finally, as an example for case (ii), consider the

example equations for the help function sub2 and the

generated unﬁnished initial rule:

sub2([Q|Qs] = Qs2 (2)

The example outputs, [], [X] of sub2 match the ﬁrst

two example outputs of the reverse-function. That is,

the unﬁnished rhs Qs2 can be replaced by a (recur-

sive) call to the reverse-function. The argument of

the call must map the inputs [X], [X, Y ] of sub2 to the

corresponding inputs [], [X] of reverse, i.e., a new help

function, sub3 is needed. This leads to the new exam-

ple set:

sub3([X]) = []

sub3([X, Y ] = [X]

The successor rule-set for the unﬁnished rule contains

two rules determined as follows: The original unﬁn-

ished rule (2) is replaced by the ﬁnished rule:

sub2([Q|Qs] = reverse(sub3([Q|Qs]))

Additionally it contains the initial rule for sub3.

4 ANALYTICALLY GENERATED

SEEDS FOR PROGRAM

EVOLUTION

As proposed above, we want to investigate whether

using IGOR2 as a preprocessor for ADATE can speed-

up ADATE’s search for a useful program. Further-

more, it should be the case that the induced program

should be as least as efﬁcient as a solution found unas-

sisted by ADATE with respect to ADATE’s evaluation

function. Obviously, coupling of IGOR2 with ADATE

becomes only necessary in such cases where IGOR2

fails to generate a completed program. This occurs if

IGOR2 was presented with a too small set of examples

or if analytically processing the given set of examples

is not feasible within the given resources of memory

and time. In these cases IGOR2 terminates with an in-

complete program which still contains unbound vari-

ables in the body of rules, namely, with missing re-

cursive calls or auxiliary functions.

To have full control over our initial experiments,

we only considered problems which IGOR2 can solve

fully automatically. We artiﬁcially created partial so-

lutions by replacing function calls by unbound vari-

ables. We investigated the following strategies for

providing ADATE with an initial seed:

For a given ADATE-ML program of the form

fun f ( ... ) : myType = raise D1

fun main ( ... ) : myType = f ( ... )

• the function f is redeﬁned using the partial solu-

tion of IGOR2,

• or the problem space becomes restricted from the

top-level by introducing the partial solution in the

function main.

• Any IGOR2 induced auxiliary functions can also

be included: as an atomic, predeﬁned function to

be called by f or as an inner function of f also

subject to transformations.

EVOLUTIONARY PROGRAMMING GUIDED BY ANALYTICALLY GENERATED SEEDS

201

5 EXPERIMENTS

We presented examples of the following problems to

IGOR2:

addition(X, Y) = Z iff Z is the sum of the two non-negative natural num-

bers X and Y. X,Y and Z are represented using peano numbers.

even integer(X) is true iff X is an even number. X is a non-negative integer.

even peano(X) is true iff X is an even number. X is a non-negative peano

number.

even pos(X) = Y iff Y is a list containing all elements on even positions in

list X.

insert(X,Y) = Z iff X is a list of elements sorted in an ascending order and

Z is a list of elements X + Y sorted in an ascending order.

last(X) = Y iff Y is identical to list X without its last element.

lasts(X) = Y iff X is a list of lists and Y is a list containing the last element

of each list in X in the order those lists appear in X.

length integer(X) = Y iff there are Y elements in the list X. Y is an integer.

length peano(X) = Y iff there are Y elements in the list X. Y is a peano

number.

member(X,Y) is true iff X is also an element in the list Y.

multlast(X) = Y iff Y is a list of equal length as the list X and all its ele-

ments are identical to the last element in X.

reverse(X) = Y iff Y is a list containing the same elements as X, only in the

reverse order.

shiftL(X) = Y iff the list Y is identical to the list X, except that the ﬁrst

element in X is on the last position in Y and all other elements are

shifted one position to the left.

shiftR(X) = Y iff the list Y is identical to the list X, except that the last

element in X is on the ﬁrst position in Y and all other elements are

shifted one position to the right.

swap(X) = Y iff the list Y is identical to the list X, except that the ﬁrst and

last element are swapped in around in Y.

swapalt(X) = Y iff the list Y is a permutation of the list X, created by alter-

natingly removing the last and ﬁrst element of X and adding them onto

the end of the empty list.

switch(X) = Y iff the list Y can be obtained from the list X by switching

every second in X with the previous element.

switch2in3(X) = Y iff the list Y can be obtained from the list X by switch-

ing the second element and every third thereafter with the previous ele-

ment in X.

To generate an initial seed for ADATE, typically

the righthand side of a recursive rule was replaced by

an unbound variable. For example, the solution for

switch provided by IGOR2 was

switch ( [] ) = []

switch ( [X] ) = [X]

switch ( [X,Y|XS] ) = [Y, X, switch(XS)]

and the third rule was replaced by

switch ( [X,Y|XS] ) = Z.

0.01

0.1

100

1000

10000

100000

1e+06

addition

even_integer

even_peano

evenpos

insert

last

lasts

length_integer

length_peano

member

multlast

reverse

shiftL

shiftR

swap

swapalt

switch

switch2in3

Creation in CPU Time (seconds)

Functional Problems

unassisted

refine

restrict

Figure 2: Creation times of best solutions.

If IGOR2 induced solutions with auxiliary func-

tions, either the function calls on the righthand side

of the rules were made known to ADATE (see Sect. 4)

or this information was obscured by again replacing

the complete righthand side by a variable.

For example, for swap, IGOR2 inferred one

atomic function last and inferred that the solution

consists of two functions that recursively call each

other as shown in ﬁgure 1. ADATE was presented with

the rule 1, 2, 5 and 6 from ﬁgure 1 where the righthand

side of rule 6 was replaced with an unbound variable.

The results were ascertained by analysing the log

ﬁles produced to document an ADATE run.

To effec-

tively compare the speciﬁcations we evaluated each

according to the time taken to generate the most cor-

rect functions. Because ADATE infers many incorrect

programs in the search process, we restricted our fo-

cus to those programs that:

• were tested by ADATE against the complete set

of given training examples,

• terminated for each training example, and

• generated a correct output for each example.

This allowed us to achieve a meaningful overview

of the performance of the speciﬁcations. For the anal-

ysis of the ADATE runs we considered the following

information:

• the elapsed time since the start of the search until

the creation of the program,

• the breakdown of the results the function pro-

duced for the examples, which in our case is the

number of results evaluated as correct, incorrect

or timed-out. Due to our evaluation restrictions,

we ﬁltered out all inferred functions which did not

attain 100% correct results with the test examples.

Technical details are given in a report by N. Crossley

available at http://www.cogsys.wiai.uni-bamberg.de/teach-

ing/ss07/p cogsys/adate-report.pdf.

IJCCI 2009 - International Joint Conference on Computational Intelligence

202

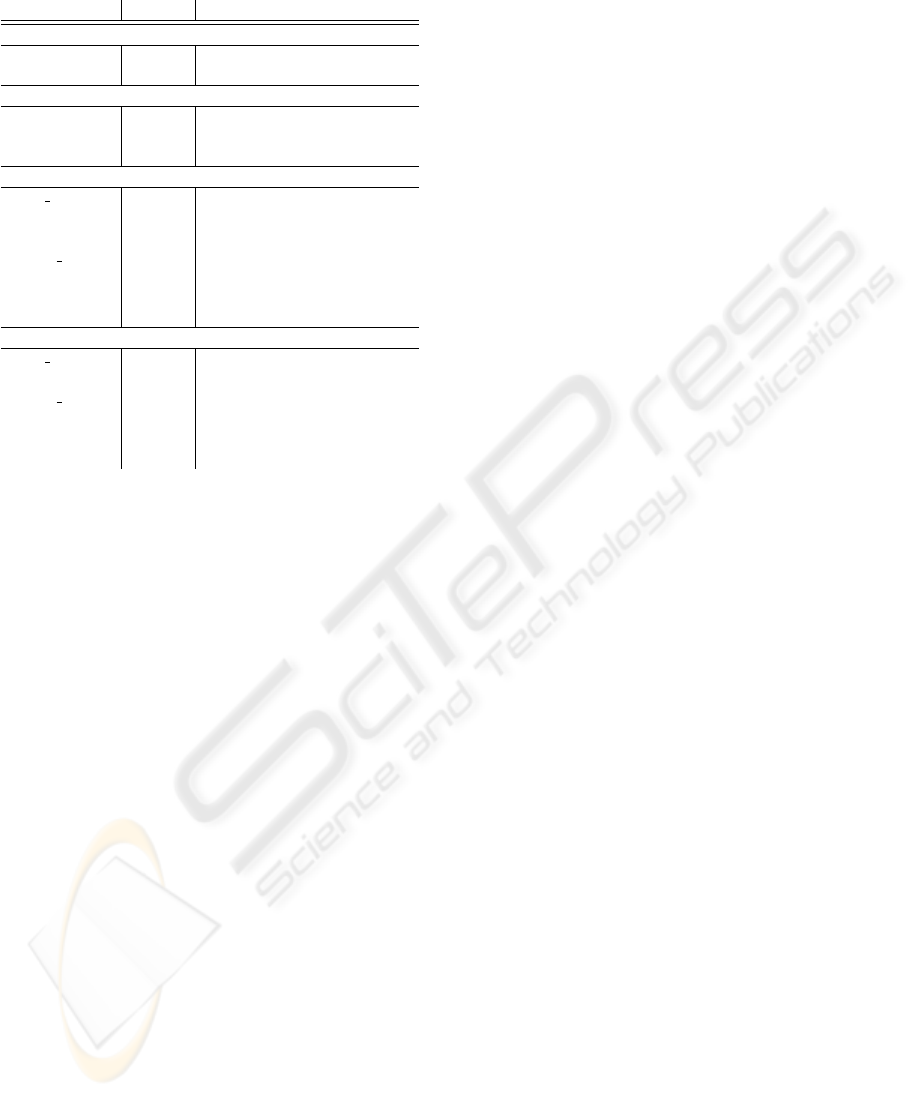
Table 1: Overview of the solutions inferred by ADATE.

# Rules Auxiliars # Rules

neither better than unassisted

addition 2 0 0

insert 3 0 0

only redeﬁned better than unassisted

member 3 0 0

shiftR 2 2 (init, last) 4

switch2in3 4 0 0

only restricted better than unassisted

even peano 3 0 0

evenpos 3 0 0

lasts 3 0 0

length peano 2 0 0

multlast 2 1 (last) 2

reverse 2 2 (last, revbutlast) 4

shiftL 3 0 0

both redeﬁned and restricted better than unassisted

even integer 3 0 0

last 2 0 0

length integer 2 0 0

swap 2 2 (last, sub) 4

swapalt 3 2 (ilast, take2nd) 4

switch 3 0 0

• an ADATE time evaluation of the inferred func-

tion. This is the total execution time taken by the

function for all the test examples as deﬁned by

ADATES built in time complexity measure.

In most cases – with the exception of addition

and insert – presenting ADATE with seeds gener-

ated by IGOR2 resulted in faster inference times (see

Figure 2).

A closer look at the results shows that quite a few

problems beneﬁted from both speciﬁcation types – re-

deﬁnition of the goal function f with a program skele-

ton as well as restriction of ADATE’s search space by

introducing the skeleton into the main program (see

Table 1). In most cases, it is clear that the right speci-

ﬁcation assistance improves the inference time for the

best possible function. Gaining additional knowledge

from the provided information, even using automatic

analytical methods such as IGOR2, assists ADATE in

producing acceptable results quicker than otherwise

would be the case. Unfortunately, it is not clear which

characteristic clearly categorises the problems into

separate groups.

6 CONCLUSIONS

We presented experiments where we can show that

providing evolutionary programming with analyti-

cally constructed seeds constrains program synthe-

sis such that search time can considerably reduced.

We compared two possibilities for providing ADATE

with program skeletons constructed with our analyt-

ical system IGOR2 and we could show that both ap-

proaches can improve performance. However, up to

now we have not found a unique criterion to decide

when to prefer which possibility. In future work we

plan to combine ADATE and IGOR2 in such a way

that IGOR2 automatically can call ADATE to help for

problems where it cannot ﬁnd a recursive program by

analytical means.

REFERENCES

Crossley, N., Kitzelmann, E., Hofmann, M., and Schmid, U.

(2009). Combining analytical and evolutionary induc-

tive programming. In Goerzel, B. et al., editors, Proc.

of the 2nd Conference on Artiﬁcial General Intelli-

gence (AGI-09), pages 19–24, Amsterdam. Atlantis.

Flener, P. and Yilmaz, S. (1999). Inductive synthesis of re-

cursive logic programs: Achievements and prospects.

Journal of Logic Programming, 41(2–3):141–195.

Hofmann, M., Kitzelmann, E., and Schmid, U. (2008).

Analysis and evaluation of inductive programming

systems in a higher-order framework. In Dengel, A.,

et al., editors, KI 2008: Advances in Artiﬁcial Intel-

ligence, number 5243 in LNAI, pages 78–86, Berlin.

Springer.

Kitzelmann, E. (2009). Analytical inductive functional pro-

gramming. In Hanus, M., editor, Proc. of the 18th In-

ternational Symposium on Logic-Based Program Syn-

thesis and Transformation (LOPSTR 2008), volume

5438 of LNCS, pages 87–102. Springer.

Kitzelmann, E. and Schmid, U. (2006). Inductive synthesis

of functional programs: An explanation based gener-

alization approach. Journal of Machine Learning Re-

search, 7(Feb):429–454.

Olsson, R. (1995). Inductive functional programming using

incremental program transformation. Artiﬁcial Intel-

ligence, 74(1):55–83.

Quinlan, J. and Cameron-Jones, R. (1995). Induction of

logic programs: FOIL and related systems. New Gen-

eration Computing, Special Issue on Inductive Logic

Programming, 13(3-4):287–312.

Summers, P. D. (1977). A methodology for LISP pro-

gram construction from examples. Journal ACM,

24(1):162–175.

Vattekar, G. (2006). Adate User Manual. Technical report,

Ostfold University College.

EVOLUTIONARY PROGRAMMING GUIDED BY ANALYTICALLY GENERATED SEEDS

203