
DERIVING MODELS FOR SOFTWARE PROJECT EFFORT
ESTIMATION BY MEANS OF GENETIC PROGRAMMING
Athanasios Tsakonas and Georgios Dounias
Decision and Management Engineering Laboratory, Department of Financial and Management Engineering
University of the Aegean, Fostini 31, str., 82100, Chios, Greece
Keywords: Software engineering, Effort estimation, Genetic programming, Symbolic regression.
Abstract: This paper presents the application of a computational intelligence methodology in effort estimation for
software projects. Namely, we apply a genetic programming model for symbolic regression; aiming to
produce mathematical expressions that (1) are highly accurate and (2) can be used for estimating the
development effort by revealing relationships between the project’s features and the required work. We
selected to investigate the effectiveness of this methodology into two software engineering domains. The
system was proved able to generate models in the form of handy mathematical expressions that are more
accurate than those found in literature.
1 INTRODUCTION
In software projects, the development effort affects
dramatically the project cost. One of the main
software engineering challenges that project
managers encounter is to estimate this human effort.
Consequently, many approaches have been used to
support such effort estimation. Contemporary
methodologies include predictive parametric models,
such as the COCOMO (Boehm, 1981) and the Price
S (Price, 2007). Other approaches are also used for
this estimation, ranging from historical analogy and
mathematical models to rules-of-thumb. Systems
that use historical analogy base their evaluation on
past projects. Mathematical models offer
relationships between project attributes, usually
derived by examination of previous projects. The
changing nature of software engineering however,
prevented many of these models from carrying
accurate results.
In this work, we propose the application of the
genetic programming paradigm (Koza, 1992), to
derive mathematical models for effort estimation
using data mining. Such a system can make use of
past software project data and automatically produce
a mathematical model. Hence, this approach can be
classified as an analogy method, since it uses
analogous data from the past, in order to produce the
regression norm. Additionally, since the result is a
mathematical expression, it also comes under the
model-based approaches. This combination seems
very attractive for the software project effort
estimation domain, combining both the data
mining’s search strength, and the GP symbolic
regression’s expression ability. The expected result
of such process can be a strong regression tool
derived by analogy, which will be also simple to use,
since it will be consisted of a mathematical formula.
In this study, we apply the genetic programming
framework in two software engineering domains,
aiming to estimate the required effort of software
projects. The application of data mining models has
become prevailing recently in software engineering,
carrying competitive results that can provide
advantages to project managers (Rodriguez et al.,
2006) (Menzies and Di Stefano, 2004). In (Shepperd
and Schofield, 1997), a case-based reasoning
approach is examined and compared with a set of
regression models. In (Aguilar-Ruiz et al., 2001), a
genetic algorithm approach manages to effectively
produce a quality set of rules for a decision-making
framework. Also, a genetic programming approach
has been applied to the assessment of human
evaluators in software projects (Boetticher et al.,
2006).
The paper is organized as follows. Next section
describes the background, presenting the effort
estimation concept for software projects and the
genetic programming principle. Section 3 deals with
the design and the implementation of the GP system.
34
Tsakonas A. and Dounias G. (2009).
DERIVING MODELS FOR SOFTWARE PROJECT EFFORT ESTIMATION BY MEANS OF GENETIC PROGRAMMING.
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval, pages 34-42
DOI: 10.5220/0002294300340042
Copyright
c
SciTePress

The results and a followed discussion are presented
in Section 4. The paper ends with our conclusion
and a description of future work in Section 5.
2 BACKGROUND
2.1 Effort Estimation for Software
Projects
When considering software projects, the dominant
cost is the labor cost. Hence, it is mandatory to
estimate the effort required for the software
development as precise as possible. In general,
aiming to estimate the software project effort
involves the definition of resources that are needed
to produce, verify and validate the software product
as well as the management of these activities. It also
involves the quantification of the uncertainty and
risk of this estimation, in those cases that this can be
useful (Lum et al., 2003).
The methods used for effort estimation can be
classified into four categories: historical analogy,
experts’ decision, use of models and rules-of-thumb.
• Historical analogy is used when there are
similar data available from the past. Usually,
it involves comparison, using measures or
data that has been recorded in previous
completed software projects. Estimations
with analogy can be made for both the high-
level overall software project effort, and for
individual tasks when developing the main
software cost estimates. The high-level
estimation is applied during the early stage of
the software project life cycle, and it usually
requires further adjustments afterwards, since
there is rarely a perfect analogy.
• Experts’ decision involves the estimates
produced by a human expert based on what
he has experienced from past projects that
carry similarity. According to (Hihn and
Habib-agathi, 1991), although this estimation
is highly subjective, it can be fairly accurate
when the expert is experienced enough in
both the software domain and the estimation
procedure.
• The use of models involves estimates
produced by mathematical or parametric cost
models. These are empirical equations that
have been derived mainly using statistical
methods. They usually concern human effort,
cost and schedule.
• The last approach that is used for effort
estimation can be rules-of-thumb. These rules
may have various forms and usually they
consist of a very simple mathematical
equation, or a percentage allocation of effort
over activities or phases, based on historical
data.
In most cases, the actual procedure of effort
estimation is performed by a combination of the
above methodologies, and the involvement of each
approach depends on the stage of the software
project. The main source of estimation during the
first stages of a software project, are the high-level
analogies and the model-based estimates. As the
project progresses and the required work become
tangible, the primary method for estimation becomes
the analogy, and the model-based estimates are used
for sanity-check.
2.2 Genetic Programming
Genetic and evolutionary algorithms are used in
various domains where a direct search method (e.g.
back-propagation in neural networks) cannot be
applied or is inefficient due to the nature of the
problem. Crossover and reproduction in genetic
programming are considered (Koza, 1992) the most
important operations. Additionally, recent
development, adopted also by our genetic
programming approach, suggests (Singleton, 1994)
that special types of mutation, such as shrink
mutation, may offer better search in the solution
space. The genetic programming process followed
through this paper, can be divided into five (5) steps:
1. Create a random population of programs
using the symbolic expressions provided.
2. Evaluate each program, assigning a fitness
value according to a pre-specified fitness
function, which actually corresponds to the
ability of the program to solve the problem.
3. Use reproduction techniques to copy existing
programs into the new generation.
4. Recombine genetically the new population
with the crossover function from a
“randomly-based” chosen set of parents.
5. Repeat steps 2–4, until the termination
criterion has been achieved.
Each node of the candidate solutions belongs to
either the function set (FS) or the terminal set (TS).
The function set contains functions available to the
GP search, and the terminal set contains constants
and input attributes. As in most common GP
approaches addressing symbolic regression
problems, in our implementation we used FS ={+, -,
*, %} where the symbol “%” stands for protected
DERIVING MODELS FOR SOFTWARE PROJECT EFFORT ESTIMATION BY MEANS OF GENETIC
PROGRAMMING
35

division (Koza, 1992). We set the data range of the
constants to [-1, 1].
3 DESIGN AND
IMPLEMENTATION
3.1 Data Preprocessing
We have tested the methodology in two effort
estimation data sets: the COCOMONASA and the
COC81. The COCOMONASA domain has been
addressed in the work of (Menzies et al., 2005),
(Chen et al., 2005) and (Menzies et al., 2005), and
the COC81 data set has been examined in
(Srinivasan and Fisher, 1995), (Menzies et al.,
2005). Both sets have become recently available by
the PROMISE repository (http://promise.site.
uottawa.ca/SERepository/) of public domain
software engineering data sets. Especially for the
COCOMONASA data, we substituted the original
descriptions of the initial data set with numerical
values, i.e. the value set {Very_Low, Low, Nominal,
High, Very_High} was substituted by the set
{0,1,2,3,4}, with the value 0 corresponding to
Very_Low and so on. In both data sets, we
performed linearization to the Lines-of-Code
(KSLOC) and months features (output feature), by
substituting the original values with their natural
logarithms. The treatment of this data, regarding
linearization, followed the conclusions found in
(Menzies et al., 2005). All the data was then
normalized in the range [-1,1], in order to improve
the search process. In candidate solutions, only
numbers belonging in that range are used; in our
experiments this approach was shown to facilitate
the exchange of genetic material and reduce the
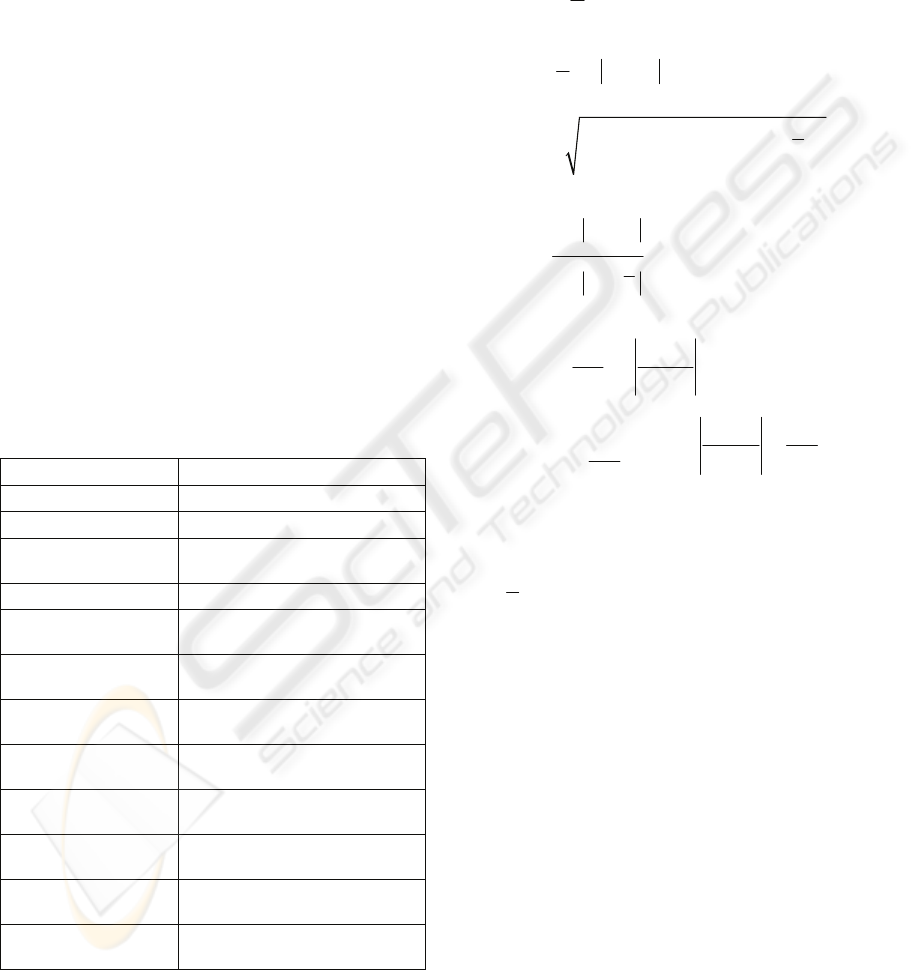
search space. To normalize, for each feature
y
, the
equation that follows is applied:
()
2
i
i
N
ym
y
r
y
y
−
=⋅
(1)
where:
()
i
N
y
: normalized value of
i
y
max min
2
yy
m
y
+
=
(2)
max min
ry y
y
=−
(3)
Table II and Table VI, summarize the available
features and their value ranges for these data sets.
3.2 Genetic Programming Setup
We have adopted a steady-state genetic process
(Rogers and Prügel-Bennett, 1999). In order to
create the initial population, four types are usually
candidates: Variable, Grow, Ramped and Ramped
Half and Half. The latter, developed by Koza (Koza,
1992), is used in the majority of the genetic
software; therefore it is followed in this work. The
tournament selection (Blickle T. and Theile, 1995)
was selected, as this is the most widely used among
the genetic software. By this process, a number of
genetic programs from the population is randomly
selected. The fitness of each member of this group is
compared and the actual best replaces the worst. The
number to randomly select individuals for each
group is usually 5 to 7. In this work, a group of 7
individuals was selected. To improve the search
process and control the solution size, an adaptive
scheme for the operation rates was followed
(Tsakonas and Dounias, 2007), starting with
crossover 80 % of the time, mutation 15% of the
time, and straight copy 5% of the time. Mutation
was further subdivided into 60% shrink mutation,
20% node mutation and 20% constant mutation
focusing this way on searching, when possible, small
candidate solutions. The crossover used is a subtree-
crossover. By this scheme, two internal nodes are
selected in each parent tree. Then, the subtree
defined by the first internal node exchanges place
with the subtree of the second internal node, as long
as the size for each derived tree is not exceeding the
maximum tree size. The aforementioned maximum
tree size was selected to be 650 nodes. All GP
parameters are summarized in Table 1.
Since having only one sample as test set is
susceptible to overfitting (Eads et al., 2002), we
performed 10-fold cross validation, keeping each
time a 10% of the data as test set. Cross validation
increases the reliability of the results of a regression
system, and the recommended number of folds is 5
to 10. In 10-fold cross validation, the training data
is split into 10 folds. Each fold is then used as the
testing data and the rest n-1 folds of data are used as
the training data to retrain the model and generate
evaluation results. The final evaluation result is
aggregated from the result of each fold. To improve
the search process, we further separated this training
data into two sets: an actual data set used for the
training (called hereinafter as actual training data
set) and a validation set. During the run, the actual
training data set is used to evaluate candidate
solutions. However, in order to promote a candidate
as the solution of the run, in our approach it is
KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval
36
required that this candidate achieves higher
regression score in the validation set as well. This
approach can help to encounter overfitting problems
that appear when using only training set (Quinlan,
1996).
3.3 Fitness Function
As fitness measure we have applied the commonly
used root mean square error (RMSE). In literature, a
variance of other measures has also been proposed
(Shepperd and Schofield, 1997). Hence, for
comparison reasons, other metrics are also
calculated, such as the mean absolute error (MAE),
and also the mean magnitude relative error
(MMRE), and the PRED(25) and PRED(30) that
have been proposed in (Conte et al., 1986). In
general, the PRED(r) function calculates the
percentage of the estimated values that have relative
error less than r. In past works, the PRED(30) has
been used for these domains and including this
measure in our study, it allows for direct
comparison. In software engineering, the standard
criteria to consider a model acceptable are
0.25MMRE ≤
and
(25) 75%PRED ≥
(Dolado, 2001).
Table 1: Genetic Programming Parameters.
Parameter Value
Population 9,000 individuals
GP implementation Steady state GP
Selection
Tournament
with elitist strategy
Tournament size 7
Crossover rate
0.8 (adaptive; see (Tsakonas and
Dounias, 2007))
Overall mutation rate
0.15 (adaptive; see (Tsakonas and
Dounias, 2007))
Straight copy rate
0.05 (adaptive; see (Tsakonas and
Dounias, 2007))
Mutation: Shrink
mutation rate
0.6
Mutation: Node
mutation rate
0.2
Mutation: Constant
mutation rate
0.2
Maximum size of
individuals (nodes)
650
Maximum number of
generations
200
In addition, we included measures which are
variance-independent, such as the root relative
square error (RRSE) and the root absolute error
(RAE), aiming to facilitate comparison with future
works, since the data in our system has been
normalized in [-1,1] and the RMSE values cannot be
used directly for comparison, unless the same
normalization is applied beforehand. The following
equations summarize the calculation of each
aforementioned measure.
()
1
2
0
1
ˆ
=
n
ii
i
R
MSE y y
n
−
=
−
∑
(4)
1
0
1
ˆ
=
n
ii
i
M
AE y y
n
−
=
−
∑
(5)
()()
11
22
00
ˆ
= /
nn
ii ii
ii
R
RSE y y y y
−−
==
−−
∑∑
(6)
1
0
1
0
ˆ
=
n
ii
i
n
ii
i
yy
RAE
yy
−
=
−
=
−
−
∑
∑
(7)
1
0
ˆ
100
=
n
ii
i
i
yy
MMRE
ny
−
=
−
∑
(8)
1
0
ˆ
1
100
PRED( )=
100
0
ii
n
i
i
yy
r
if
r
y
n
otherwise
−
=
⎧
⎪
−
⎪
≤
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
∑
(9)
where:
i
y
: actual value of case i
ˆ
i
y
: estimated value of case i
i
y
: mean value of test set cases
n : number of cases in test set
r
: value (range) for which the PRED function
is calculated, usually set to 25 or 30
Having discussed the system design, in the
following session we shall apply the methodology in
the software engineering domain.
4 RESULTS AND DISCUSSION
4.1 COCOMONASA Domain
The COCOMONASA dataset consists of 60 NASA
projects from different centers for projects from the
1980s and 1990s. This data comes from the
aerospace software domain. There are 17 attributes
that are all numeric: 15 attributes are the effort
multipliers, one is the Lines-of-Code (LOC) and one
attribute is the actual development effort. The LOC
DERIVING MODELS FOR SOFTWARE PROJECT EFFORT ESTIMATION BY MEANS OF GENETIC
PROGRAMMING
37

variable has been estimated directly or computed
beforehand, using function point analysis (Dreger,
1989). The task is to tune a new cost model, for a
given background knowledge. In (Menzies et al.,
2005), a very simple calibration method (called
COCONUT) achieved PRED(30)=70% and
PRED(20)=50%. These results were seen in 30
repeats of an incremental cross-validation process.
In the same paper, two cost models are compared;
one based in lines of code and one using additionally
14 so-called effort multipliers. The use of only lines
of code resulted into the loss 10 to 20 PRED(r)
points. In (Chen et al., 2005), a feature subset
selection (FSS) is applied to this software effort
data. The paper shows that FSS can dramatically
improve cost estimation. Table 2 summarizes the
available features and their value ranges. Further
details on each feature can be found in (Boehm,
1981).
Table 2: Data Features and Value Range.
Variable Description Max Min
rely Required software
reliability
4 1
data Data base size 4 1
cplx Process complexity 5 1
time Time constraint for
CPU
5 2
stor Main memory
constraint
5 2
virt Machine volatility 3 1
turn Turnaround time 3 1
acap Analysts capability 4 2
aexp Application
experience
4 2
pcap Programmers
capability
4 2
vexp Virtual machine
experience
3 1
lexp Language
experience
3 0
modp Modern
programming
practices
4 1
tool Use of software
tools
4 0
sced Schedule constraint 3 1
ln(KSLOC) Software size lines-
of-code
6.04 0.788
ln(months) Effort in months 8.08 2.128
Table 3 summarizes our results per fold run, and
includes the mean and the standard deviation for
each measure and feature of the solution. The
column Generation is the generation in which the
solution was found, and the Size column is the
number of nodes of the solution tree (e.g. the
complexity of the derived mathematical formula).
As it can be seen from Table 3, the derived solutions
can vary significantly in their size, depending on the
fold used. The following solution that was derived in
fold #7, is surprisingly small, with only two features
used (apart KSLOC), and it achieved 100%
PRED(25).
(
)
(
)
(
)
(
)
(
)
(
)
ln ln 0.03
NN
NN
months KSLOC virt turn
⎡⎤
=−⋅+
⎢⎥
⎣⎦
(10)
where
()
N
⋅ denotes that the normalized values
of the corresponding variables are used.
Table 3: GP 10-Fold Cross Validation Results.
Fold # RMSE MAE RRSE RAE MMRE
1 0.088 0.071 0.202 0.186 0.158
2 0.029 0.026 0.077 0.080 0.084
3 0.093 0.082 0.195 0.191 0.189
4 0.148 0.105 0.653 0.510 0.302
5 0.276 0.181 0.617 0.458 0.328
6 0.061 0.040 0.160 0.120 0.112
7 0.060 0.048 0.104 0.093 0.098
8 0.168 0.142 0.416 0.403 0.223
9 0.148 0.103 0.317 0.270 0.677
10 0.154 0.118 0.349 0.303 0.424
Mean 0.122 0.092 0.309 0.261 0.259
StdDev 0.072 0.048 0.202 0.154 0.184
Fold # PRED(25) PRED(30) Size Generation
1 66.7% 100.0% 511 14
2 100.0% 100.0% 313 13
3 66.7% 83.3% 467 46
4 50.0% 66.7% 73 135
5 50.0% 50.0% 301 148
6 100.0% 100.0% 509 100
7 100.0% 100.0% 7 8
8 50.0% 66.7% 5 4
9 66.7% 66.7% 195 14
10 50.0% 50.0% 3 4
Mean 70.0% 78.3% 238 49
StdDev 21.9% 20.9% 211 57
It is worth to note that KSLOC and turn variables
are also present in all derived models in the work of
(Chen et al., 2005), while the virt variable occurs
only in 1 of the 10 models. As stated previously, the
months and KSLOC variables used in our study have
KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval
38

been changed to the natural logarithms of the
original data set values. If we perform the reverse
conversion (e.g. de-normalizing), we result into the
following simple relation between the original data
set values:
0.3803ln( ) 0.03 0.03 0.2949
0.3358
KSLOC virt turn
months e
−− +
=
(11)
In Table 4, the occurrence of each feature in the
solutions found for all folds is shown.
Table 4: Feature Frequency.
Variable Times Variable Times
ln(KSLOC) 10 virt 4
aexp 6 pcap 4
rely 5 vexp 4
data 5 tool 4
time 5 sced 4
stor 5 cplx 3
turn 5 acap 3
lexp 5 modp 2
Table 5 compares our results for PRED(30) to
those found in literature with best values in bold. As
it can be seen, our system achieved a higher
PRED(30) rate as compared to past works, in both
the average resulted value and the highest one
produced. On the other hand, in this table we present
a high standard deviation in our system.
Table 5: PRED(30) Results Comparison.
Publication Method Avg. Std.De
v
Best
(Menzies et
al., 2005)
coconut n/a n/a 70,0%
(Chen et
al., 2005)
wrapper FSS 76.7% 7.3%* 81,3%
(Menzies et
al., 2005)
lsr_num_ln 69.7% 11.1% n/a
(Menzies et
al., 2005)
lsr_em_ln 68.5% 12.5% n/a
(Menzies et
al., 2005)
m5_num_ln 73.5% 10.7% n/a
(Menzies et
al., 2005)
m5_em_ln 69.7% 10.5% n/a
(Menzies et
al., 2005)
m5_em_loc_ln 60.5% 9.6% n/a
(Menzies et
al., 2005)
lsr_em_loc_ln 60.5% 9.6% n/a
(Menzies et
al., 2005)
m5_num_loc_ln 55.3% 11.7% n/a
(Menzies et
al., 2005)
lsr_num_loc_ln 40.8% 11.7% n/a
Table 5: PRED(30) Results Comparison (Cont.).
(Menzies et
al., 2005)
m5_em 41.0% 14.4% n/a
(Menzies et
al., 2005)
m5_num 41.5% 11.6% n/a
(Menzies et
al., 2005)
m5_num_loc 42.0% 8.9% n/a
(Menzies et
al., 2005)
lsr_num_loc 41.2% 12.7% n/a
(Menzies et
al., 2005)
lsr_em_loc_ln 40.2% 8.4% n/a
(Menzies et
al., 2005)
lsr_num 31.0% 12.7% n/a
(Menzies et
al., 2005)
lsr_em 28.7% 8.4% n/a
This study
genetic
programming
78.3
%
20.9% 100%
* best reported value
The reason for this is that we record here the
standard deviation of PRED(30) encountered during
the 10-fold cross validation, which results from
evaluating different test data sets (e.g. for each fold
validation). On the other hand, in (Chen et al., 2005)
the test sets are selected randomly for each run,
allowing for potential set overlapping; in (Menzies
et al., 2005) the standard deviation is reported over
30 runs on the same data set. Hence, taking into
respect the (completely) different test sets
encountered, we consider the high value of our
system’s standard deviation as being a natural result.
4.2 COC81 Domain
The COC81 dataset consists of 63 instances. This
data comes from a variety of domains such as
financial, engineering and science projects. There
are 17 attributes that are all numeric: 15 attributes
are the effort multipliers, one is the Lines-of-Code
(LOC) and one attribute is the actual development
effort. There are no missing attributes. In (Srinivasan
and Fisher, 1995), a variety of methods are
examined into a related data set, including neural
networks, regression trees, COCOMO and the SLIM
model (Putnam, 1978). The neural networks and
function-point based prediction models
outperformed regression trees, and the latter
outperformed COCOMO and the SLIM model.
Table 6 summarizes the available features and their
value ranges. A detailed description for these
features appears in (Boehm, 1981). As it can be seen
from Table 7, the derived solutions can vary
significantly in their size, depending on the fold
DERIVING MODELS FOR SOFTWARE PROJECT EFFORT ESTIMATION BY MEANS OF GENETIC
PROGRAMMING
39

used. The following solution that was derived in fold
#1, has only one feature used (apart KSLOC), and it
achieves 57.1% PRED(25).
(
)
(
)
(
)
(
)
(
)
ln ln 0.15
N
NN
months KSLOC virt=−⋅
(12)
where
()
N
⋅ is a symbol for the normalized
values of the corresponding variables, as previously.
Table 6: Data Features and Value Range.
Variable Description Maximum Minimum
rely Required software
reliability
1.400 0.750
data Data base size 1.160 0.940
cplx Process
complexity
1.650 0.700
time Time constraint for
CPU
1.660 1.000
stor Main memory
constraint
1.560 1.000
virt Machine volatility 1.300 0.870
turn Turnaround time 1.150 0.870
acap Analysts capability 1.460 0.710
aexp Application
experience
1.290 0.820
pcap Programmers
capability
1.420 0.700
vexp Virtual machine
experience
1.210 0.900
lexp Language
experience
1.140 0.950
modp Modern
programming
practices
1.240 0.820
tool Use of software
tools
1.240 0.830
sced Schedule
constraint
1.230 1.000
ln(KSLOC) Software size
lines-of-code
7.048 0.683
ln(months) Effort in months 9.341 1.775
The variable KSLOC is also present in all derived
models in the work of (Menzies et al., 2005), and the
virt variable occurs in 9 of the 10 models. As stated
previously, the months and KSLOC variables used in
our study have been changed to the natural
logarithms of the original data set values. By
performing the reverse necessary conversions (e.g.
de-normalizing), we conclude to the following
simple equation between the original data set values:
1.188ln( ) 2.637 20.05KSLOC virt
months e
−+
=
(13)
Table 8 summarizes the occurrence of each
feature to the solutions found in all folds.
Table 7: GP 10-Fold Cross Validation Results.
Fold # RMSE MAE RRSE RAE MMRE
1 0.174 0.119 0.449 0.337 0.465
2 0.147 0.133 0.389 0.408 0.836
3 0.214 0.156 0.782 0.647 0.465
4 0.206 0.162 0.741 0.761 0.949
5 0.294 0.231 0.933 0.841 1.895
6 0.221 0.192 0.700 0.734 1.027
7 0.305 0.224 0.525 0.441 1.411
8 0.219 0.169 0.352 0.332 1.209
9 0.208 0.183 0.332 0.351 0.458
10 0.201 0.182 0.376 0.403 0.696
Mean 0.219 0.175 0.558 0.526 0.941
StdDev 0.048 0.035 0.214 0.197 0.467
Fold # Size
PRED
(25)
PRED
(30)
Generation
1 5 57.1% 57.1% 2
2 107 42.9% 42.9% 8
3 7 50.0% 50.0% 3
4 11 50.0% 50.0% 8
5 5 33.3% 33.3% 6
6 23 50.0% 50.0% 8
7 15 50.0% 50.0% 10
8 13 50.0% 50.0% 7
9 5 50.0% 50.0% 13
10 7 42.9% 42.9% 5
Mean 20 47.6% 47.6% 7
StdDev 31 6.4% 6.4% 3
Table 9 compares our results for PRED(30) to
those found in literature. The best values are shown
in bold. The low success rates for all models reflect
the fact these COC81 data concern projects from
different domains (e.g. financial, engineering, etc.)
while the COCOMONASA data addressed the
aerospace project domain only, which follows the
stratification hypothesis (Boehm et al., 2000). A
comparison to the results of (Srinivasan and Fisher,
1995) is not included, since in that publication, an
extended feature set was used (e.g. 39 attributes
were used, instead of the 17 ones that have become
publicly available in the PROMISE repository). As it
can be observed in the results presented in Table 9,
our system outperformed those found in literature, in
both the average and best PRED(30) values, as well
as to its standard deviation.
KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval
40

Table 8: Feature Frequency.
Variable Times Variable Times
ln(KSLOC) 10 cplx 2
virt 6 acap 2
stor 4 turn 1
rely 3 time 1
vexp 2 pcap 1
tool 2 aexp 1
sced 2 modp 0
lexp 2 data 0
Table 9: PRED(30) Results Comparison.
Publication Method Average
Std.
dev
Best
(Chen et al., 2005) *
wrapper
FSS
45.8% 9.3%
51,3
%
(Menzies et al., 2005)
lsr_num_
ln
44.3% 10.8% n/a
(Menzies et al., 2005)
lsr_em_l
n
40.0% 9.7% n/a
(Menzies et al., 2005)
m5_num
_ln
39.7% 13,7% n/a
(Menzies et al., 2005)
m5_em_l
n
38.4% 9.2% n/a
(Menzies et al., 2005)
m5_em_l
oc_ln
21.7% 8.5% n/a
(Menzies et al., 2005)
lsr_em_l
oc_ln
21.7% 8.5% n/a
(Menzies et al., 2005)
m5_num
_loc_ln
20.6% 6.9% n/a
(Menzies et al., 2005)
lsr_num_
loc_ln
20.6% 6.9% n/a
(Menzies et al., 2005) m5_em 15.4% 8.4% n/a
(Menzies et al., 2005) m5_num 13.7% 8.7% n/a
(Menzies et al., 2005)
m5_num
_loc
11.7% 6.9% n/a
(Menzies et al., 2005)
lsr_num_
loc
11.3% 6.7% n/a
(Menzies et al., 2005)
lsr_em_l
oc_ln
11.3% 6.7% n/a
(Menzies et al., 2005) lsr_num 9.4% 6.7% n/a
(Menzies et al., 2005) lsr_em 7.9% 6.8% n/a
(Menzies et al, 2006)*
coc81:ki
nd.max
47% 51% n/a
This study
genetic
program
ming
47.6% 6.4%
57.1
%
* best reported value
5 CONCLUSIONS AND FURTHER
RESEARCH
In respect to the software engineering, the needs for
accurate and easily applicable estimating models
have become increasingly demanding recently. In
this work, a genetic programming approach for
symbolic regression was proposed for the problem
of software project effort estimation. Data
preprocessing took place in order to enhance the
search process. This genetic programming model
was further configured with the incorporation of
cross-validation technique and a validation set.
Special attention was paid into the operators to be
included and the operations rates in order to boost
search and increase solution comprehensibility. The
model was then effectively applied into two software
engineering domains that have recently become
publicly available from the PROMISE data
repository. In both domains, our system was proved
capable to produce results that not only carry higher
regression accuracy as compared to those found in
literature, but also are interpretable mathematical
formulas, easy to be used by project managers. The
overall approach was shown fairly robust to be
applied into more software engineering estimation
domains.
Further work involves the application of genetic
programming into more effort estimation domains,
as well as to other software engineering problems,
such as defect prediction and text mining tasks for
analyzing code comprehensibility. Additionally, we
plan to apply this methodology using incrementally
smaller test sets, in order to draw conclusions on
incremental holdout results (Menzies et al., 2005).
Also, we aim to apply strongly typed genetic
programming (Montana, 1995) into the datasets of
this study. We expect that a strongly typed GP
approach will further improve the resulted formula’s
precision, since it will guide the search process only
through the subspace of rational solutions. Finally,
among further research is applying to the examined
domains other computational intelligence models,
such as the Takagi-Sugeno fuzzy rule-based model
(Takagi and Sugeno, 1985), for the production of
comprehensive, fuzzy competitive rules.
REFERENCES
Aguilar- Ruiz J.S., Ramos I., Riquelme J.C. and Toro M. ,
2001, An evolutionary approach to estimating
software development projects, Information and
Software Technology, 43, pp. 875-882.
Blickle T. and Theile L., 1995, A mathematical analysis
DERIVING MODELS FOR SOFTWARE PROJECT EFFORT ESTIMATION BY MEANS OF GENETIC
PROGRAMMING
41

of tournament selection, in: L.J. Eshelman, ed., Proc.
of the 6
th
International.Conference on Genetic
Algorithms, Lawrence Erlbaum Associates, Hillsdale,
New Jersey, pp. 9-16.
Boehm B., 1981, Software Engineering Economics,
Prentice-Hall.
Boehm B., Horowitz E., Madachy R., Reifer D., Clark
B.K., Steece B., Brown A.W., Chulani S. and Abts C.,
2000, Software Cost Estimation
Boetticher, G., Lokhandwala, N., James C. Helm, 2006,
Understanding the Human Estimator, 2
nd
Int’l.
Predictive Models in Soft. Eng. (PROMISE)
Workshop, 22
nd
IEEE Int’l. Conf. on Soft.
Maintenance, PA, USA, Sep. 2006.
Chen Z., T. Menzies, D. Port and B. Boehm, 2005, Feature
Subset Selection Can Improve Software Cost
Estimation Accuracy, in Proc. 1
st
Int’l. Predictive
Models in Soft. Eng. (PROMISE) Workshop St. Louis,
MI, USA.
Conte S.D, Dunsmore H.E. and Shen V., 1986, Software
Engineering Metrics and Models, Benjamin-
Cummings.
Dolado J.J., 2001, On the problem of the software cost
function, Information and Software Technology, 43,
pp. 61-72.
Dreger J., 1989, Function Point Analysis, Englewood
Cliffs, NJ, Prentice Hall.
Eads D., Hill D., Davis S., Perkins S., Ma J., Porter R. and
Theiler J., 2002, Genetic Algorithms and Support
Vector Machines for Time Series Classification, in
Proc. SPIE 4787, pp. 74-85
Hihn J. and Habib-agathi H., 1991, Cost estimation of
Software Intensive Projects: A survey of Current
Practices, in Proc. of the 13
th
IEEE Int’l. Conf. Soft.
Eng., May 13-16.
Koza J.R., 1992, Genetic Programming: On the
Programming of Computers by Means of Natural
Selection, Cambridge, MA, MIT Press.
Lum K., Bramble M., Hihn J., Hackney J., Khorrami M.
and Monson E., 2003, Handbook of Software Cost
Estimation, Jet Propulsion Laboratory, Pasadena, CA,
USA.
Menzies T., Z. Chen, J. Hihn, K. Lum, Selecting Best
Practices for Effort Estimation, IEEE Transactions
Software Engineering, Vol. 32, Number 11,
November, 2006
Menzies T., D. Port, Z. Chen, J. Hihn and S. Stukes, 2005,
Validation Methods for Calibrating Software Effort
Models, in Proc. ICSE 2005, May 15-21, St.Louis,
MI, USA.
Menzies T., Chen D.P.Z. and Hihn H., 2005, Simple
Software Cost Analysis: Safe or Unsafe ?, in Proc. 1
st
Int’l. Predictive Models in Soft. Eng. (PROMISE)
Workshop, St. Louis, MI, USA.
Menzies T. and Di Stefano J.S. , 2004, How Good is your
Blind Spot Sampling Policy?, in Proc. of 8
th
IEEE Int’l
Symp. on High Assurance Systems Eng., March 25-26,
Tampa, FL, USA.
Montana D.J., 1995, Strongly Typed Genetic
Programming, Evolutionary Computation, 3:2.
Price S, 2007, URL: http://www.pricesystems.com.,,,
Putnam L.H, 1978, A general empirical solution to the
macro software sizing and estimating problem, IEEE
Trans. Soft. Eng., 4:4, April 1978, pp 345-61.,
Quinlan J.R., 1996, Bagging, boosting, and C4.5, in Proc.
13
th
Nat.Conf. Art. Intell., pp.725-30.
Rodriguez D., Cuadrado J.J., Sicilia M.A. and Ruiz R. ,
2006, Segmentation of Software Engineering Datasets
Using the M5 Algorithm, in V.N.Alexandrov et al.
(Eds.): ICCS 2006, Part IV, LNCS 3994, Springer-
Verlag, pp. 789-796.
Rogers A. and Prügel-Bennett A., 1999, Modeling the
dynamics of steady-state genetic algorithms, in: W.
Banzhaf and C. Reeves, eds., Foundations of genetic
algorithms, Morgan Kaufmann, San Francisco, pp.
57-68.
Singleton A., 1994, "Genetic Programming with C++",
BYTE Magazine, February 1994
Shepperd M. and Schofield C., 1997, Estimating software
project effort using analogies, IEEE Trans. Soft. Eng.,
23 (12), Nov. 1997.
Srinivasan K.and Fisher D., 1995, Machine Learning
Approaches to Estimating Software Development
Effort, IEEE Trans. Soft. Eng., 21(2), Feb. 1995, pp.
126-37.
Takagi T. and Sugeno M., 1985, Fuzzy Identification of
Systems and its Application to Modeling and Control,
IEEE Trans. On Systems, Man and Cybernetics, 17,
pp. 295-301
Tsakonas A. and Dounias G., 2007, Evolving Neural-
Symbolic Systems Guided by Adaptive Training
Schemes: Applications in Finance, Applied Artificial
Intelligence, 21:7, pp. 681-706.
KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval
42
