
A
METHOD FOR APPROXIMATION TO ONTOLOGY REUSE
PROBLEM
Eleni Tsalapati, Giorgos Stamou and Giorgos Koletsos
School of Electrical and Computer Engineering, National Technical University of Athens
GR-15773 Zographou, Athens, Greece
Keywords:
Ontology Reuse, Module, Locality.
Abstract:
We describe a methodology that approximates the safety condition in the integration of ontologies. Intuitively,
the safety condition ensures that, after the reuse, the external ontology remains intact. It was recently proved
that it is a problem of high complexity to examine whether this condition holds. In order to approximate the
problem, we suggest a method by which the ontology designer that reuses concepts from an ontology network
will be informed about the degree in which the safety is violated and according to this information she can
choose the appropriate ontologies to reuse concepts from.
1 INTRODUCTION
Today, one can find in the Web a vast number of
ontologies on the same domain in different levels
of granularity or in different domains, available for
reuse. The research conducted on the problem of
ontology reuse process, regardless of the approach
method, has revealed some very crucial obstacles. It
is essential that the ontology integration should be
carried out in such a way that the consequences of
the axioms of the external ontology are not changed
when its elements are reused in the ontology under
development. It is proved (Lutz et al., 2007) that to
question whether this condition holds, even in lan-
guages of very low expressivity, is practically unde-
cidable (2EXPTIME-complete).
In this paper, we assume that the ontology de-
signer wishes to generalise (e.g., add new supercon-
cepts) some of the concepts of the ontology under
development by importing concepts from an external
one. At the same time though, we do not prevent the
developer from refining (e.g., add new subconcepts)
some concepts, as well. However, the simultaneous
generalization and refinement from the same external
ontology may introduce new knowledge to this ontol-
ogy. For instance, if the ontology developer reuses
in his ontology P the concepts X, Y from the ontol-
ogy Q to create the following axioms: A v Q : X and
Q : Y v B, and the axiom B v A is already present
in P, then the axiom Q : Y v Q : X is implied, which
may not hold in Q. In the same way, non anticipated
changes may also occur in the ontology P.
We have developed a tool that provides the on-
tology developer with an estimation of the changes
caused not only in the external ontology, but also in
the ontology under development. Being aware of the
effects of the integration of the two ontologies, the
user is enabled to choose firstly, whether he will refine
a concept or not, and secondly, the most appropriate
external ontology to choose concepts from, based on
the criterion “to cause the least possible damage”.
2 PRELIMINARIES
We consider ontologies to be a set of axioms in a
descriptions logic language L. Description Logic is
the language that underlies the modern ontology lan-
guages, like OWL DL. The signature of an ontology
O is the set of atomic concepts (C), atomic roles (R)
and individuals (I) that occur in O. An ontology based
on S HOIQ language contains also nominals.
The notions of logical entailment, S-
interpretation, restriction of an S-interpretation
and satisfiability follow the definitions of the D.
L. Handbook (Baader et al., 2003). We omit their
description in this paper due to limited space. An
expansion of an S
1
-interpretation I
1
to S is an
S-interpretation I such that I |
S
1
= I
1
(Grau et al.,
2007b). In bottom expansion, atomic concepts and
roles, not in S are interpreted as Bottom (⊥), whereas
416
Tsalapati E., Stamou G. and Koletsos G. (2009).
A METHOD FOR APPROXIMATION TO ONTOLOGY REUSE PROBLEM.
In Proceedings of the International Conference on Knowledge Engineering and Ontology Development, pages 416-419
DOI: 10.5220/0002296304160419
Copyright
c
SciTePress

in top expansion, they are interpreted as Top (>).
The reuse of an external ontology can lead to un-
desirable side effects, such as the entailment of new
axioms or even inconsistencies involving the reused
vocabulary. However, a safe ontology for a signature
S, enables the implementation of the ontology reuse
process without any fallacies:
Definition 2.1. (Safety for a Signature, (Grau et al.,
2007b)). Let L be an ontology language, and let P
be an ontology and S a signature over L. We say that
P is safe for S w.r.t. L , if for every ontology Q over
L with Sig(P) ∩ Sig(Q) ⊆ S, we have that P ∪ Q is a
conservative extension of Q w.r.t. L.
The conservative extension property ensures that the
additional axioms of the ontology under development
will not add any new consequences over the vocabu-
lary of the reused ontology.
Following, we describe the syntactic definitions
>-locality and ⊥-locality concepts (Jim
´
enez-Ruiz
et al., 2008), as they are heavily used in our method.
Definition 2.2. (Syntactic ⊥-Locality and >-Locality for
SHIQ). Let S be a signature. An axiom a is ⊥-local w.r.t. S
(>-local w.r.t S) if a ∈ Ax(S), as defined in (a) ((b)), where
C and R denote arbitrary concepts and roles. An ontology
O
is
⊥
-local (
>
-local) w.r.t. S if
a
is
⊥
-local (
>
-local) w.r.t.
S for all a ∈ O.
(a) ⊥ − Locality. Let A
⊥
, R
⊥
6∈ S, C
⊥
∈ Bot(S), C
>
(i)
∈
Top(S), n ∈ N \{0}:
Bot(S) ::= A
⊥
|⊥ | (¬C
>
)| (C uC
⊥
)| (C
⊥
u
uC) |(∃R
⊥
.C) |(∃R.C
⊥
)|(≥ nR
⊥
.C) |(≥ nR.C
⊥
)
Top(S) ::= > |(¬C
⊥
)| (C
>
1
uC
>
2
)| ≥ 0R.C
Ax(S) ::= C
>
v C |C v C
⊥
|R
⊥
v R |Trans(R
⊥
)
(b) > − Locality. Let A
>
, R
>
6∈ S, C
⊥
∈ Bot(S), C
>
(i)
∈
Top(S), n ∈ N \ {0}:
Bot(S) ::= (¬C
>
)| ⊥ |(C uC
⊥
)| (C
⊥
u
uC) |(∃R.C
⊥
)| (≥ nR.C
⊥
)
Top(S) ::= A
>
|> | (¬C
⊥
)|(C
>
1
uC
>
2
)
|(∃R
>
.C
>
)|(≥ nR
>
.C
>
)| ≥ 0R.C
Ax(S) ::= C
>
v C |C v C
⊥
|R v R
>
|Trans(R
>
)
If an ontology P is ⊥-local or >-local w.r.t. a signa-
ture S, then P is safe for S (Grau et al., 2007a). The
simultaneous refinement and generalization of an on-
tology from the same external one, may compromise
safety (Jim
´
enez-Ruiz et al., 2008). Particularly, when
the signature S is to be refined (generalized), the on-
tology P must be ⊥-local (>-local) w.r.t. S. Conse-
quently, in the case of refinement of the signature S
(and thus generalization of P) the set of non-⊥-local
axioms contains the axioms that threaten the safety.
3 METHOD FOR PARTIAL
ONTOLOGY REUSE
The goal of this method is to enable the ontology de-
veloper to refine and generalise several concepts from
the same external ontology by providing him with an
estimation of the non-safety degree resulted from this
ontology reuse. Particularly, we are interested in pro-
viding the user not only with the affected part of the
external ontology Q, but also with the non anticipated
changes (new axioms over the language of P) caused
in the ontology under development.
According to the previous paragraph the set of the
non-⊥-local axioms w.r.t. Sig(Q) equals to a super-
set of the axioms that threaten the safety of the inte-
gration. To clarify this, we demonstrate the follow-
ing example, in which two ontologies developed for
the BOEMIE Project (www.boemie.org), the Athletic
Event Ontology, aeo, and the Geographic Information
Ontology, gio are used.
Example 3.1. Supposing that SportsPOI is concept of
aeo ontology and aeo reuses concepts from gio, then
the following is a non-⊥-local axiom wrt Sig(gio):
gio:Stadium v SportsPOI (1)
If the following axioms also exist in aeo ontology :
gio:Stadium v ∃isLocatedIn.Cityu
uSportsPOI u ∃hasArea.TrackArea
(2)
∃isLocatedIn.City u SportsPOI v
gio:ManMadeFeature
(3)
Then following new axiom of gio is implied:
gio:Stadium v gio:ManMadeFeature (4)
Apart from the fact that this axiom might introduce an
inconsistency in gio, it also adds a new definition on
the concept Stadium, that did not initially exist. We
call the axiom (1) as directly affected axiom.
The set of directly affected axioms is the remain-
ing set of non-⊥-local axioms after the abstraction of
the axioms already included in gio:
Definition 3.2. Let L be an ontology language and P and
Q be ontologies over L. If ontology P reuses concepts from
ontology Q, then the set A of the directly affected axioms of
P for Q is:
A = {a ∈ P|a : non − ⊥ − localAxiom w.r.t.Sig(Q)∧
∧a 6∈ Q}
In Example 3.1 the definition of the concept Stadium
of gio ontology, is changed. To approximate the sub-
set of the reused entities affected by this integration it
suffices to find the subsumed concepts of the set of di-
rectly affected axioms. For instance, in Example 3.1,
the Stadium concept is a directly affected entity. At
A METHOD FOR APPROXIMATION TO ONTOLOGY REUSE PROBLEM
417

present this theory concerns only simple axioms (ax-
ioms of the form A v C, where A is atomic concept).
The set of directly affected entities of an axiom a by
an ontology P is symbolized as DAE(a,P). The set of
directly affected entities of an ontology Q by an on-
tology P is symbolized as DAE(Q,P) and represents
the set of affected entities of each axiom of Q.
The modification of the Stadium concept defini-
tion also affects all the concepts that are related di-
rectly or indirectly to Stadium in gio. To make this
more clear we demonstrate the following example:
Example 3.3. Suppose that gio contains the following
axioms:
IndoorStadium v Stadium (5)
OutdoorStadium v Stadium (6)
then the concepts IndoorStadium and OutdoorStadium
are also altered. The modification of these definitions
is propagated to other concepts related to them. For
instance, the definition of IndoorAthleticCenter con-
cept is also affected:
IndoorAthleticCenter v
∃contains.IndoorStadium
(7)
Thus, to find the total set of the affected concepts is
suffices to find all the subconcepts, directly and in-
directly related to an affected entity. To achieve this
we calculate, the set of >-local axioms of ontology Q
w.r.t. S
0
= Sig(Q) \ S, where S is the set of affected
entities of Q by ontology P. Intuitively, in this way,
all affected entities become equivalent to the top con-
cept and thus, the set of >-local axioms includes the
subsumption axioms that their right hand side concept
is affected. If an axiom is found to be >-local then it
is added to the set of affected axioms and its directly
affected entities are abstracted from S
0
, thus the next
checked axiom is tested w.r.t. >-locality for the new
S
0
. More formally, the set of affected axioms is de-
fined as:
Definition 3.4. Let P and Q be ontologies, such that
P reuses concepts from Q. Then the set of affected
axioms of Q by ontology P is defined as:
AA(Q,P) = {a ∈ Q|a : > − local w.r.t.(Sig(Q)\
(DAE(Q,P) ∪ DAE(Q,AA(Q, P))))}
Similarly, if P is the ontology under development and
P
0
the ontology P before the reuse of the external
ontology, the set of affected axioms of the ontology
P
0
is AA(P
0
,P). To calculate the rate of affected ax-
ioms of an ontology Q from an ontology P, r(Q, P),
it suffices to divide the number of axioms of the set
AA(Q,P) to the total number of axioms of Q (i.e.
r(Q, P) = | AA(Q,P) | / | Q |).
Having the rates r(Q,P) and r(P
0
,P), we can cal-
culate the total cost of the reuse process in relation to
two weights w
1
and w
2
, that determine how important
is the particular change to each ontology:
Definition 3.5. (Total Cost) Let P and Q be two on-
tologies, S the set of entities of Q reused by P and
w
1
, w
2
> 0 the weights. The total cost of the ontology
reuse procedure is:
TotalCost =
w
1
· r(Q,P) + w
2
· r(P
0
,P)
w
1
+ w
2
Following, we demonstrate the algorithm that com-
putes the affected axioms of ontology Q from P.
Algorithm 1: AA(Q,DAE(Q,P)).
Input:
DAE(Q,P):set of Directly Affected Entities of Q from P
Q: external ontology
Output:
Q
2
: Affected Axioms
1:
S ← (Sig(Q) \ DAE(Q,P)), Q
1
←
/
0, Q
2
← Q
2: while
(¬
empty
(Q
2
)){
3: forall
a ∈ {a|a ∈ Q
2
∧ a : OW LSubClassAxiom} {
4: if
(> − locality −test(a,S)){
5:
Q
1
= Q
1
∪ {a}
6:
S = S \ {LHS(a)}
7:
Q
2
= Q \ Q
1
}
8: else
{Q
2
= Q
2
\ {a}}
9:
}}
10: return
Q
2
For the locality-test we used the method provided by
PRoSE (http://krono.act.uji.es/people/Ernesto/safety-
ontology-reuse/proSE-current-version). The LHS
function returns the left hand side of a subclass ax-
iom.
Proposition 3.6. For every input P and Q, the Algo-
rithm 1 computes the affected axioms of the partici-
pating ontologies.
Proof (Sketch). The algorithm terminates as in every
iteration of the while loop the size of Q
2
decreases.
Initially, all the >-local axiom are transferred from
Q
2
to Q
1
, and then the rest axioms, which are non->-
local, are removed from Q
2
. Note, that the syntactic
locality test has polynomial complexity.
The output AA(Q, DAE(Q,P) is the set of affected
axioms of Q from P, as every axiom that is nei-
ther in Q
1
nor in Q
2
is non->-local wrt Sig(Q) \
(DAE(Q,P)∪DAE(Q,AA(Q,P))), since, as indicated
in line:8, it remains in the set Q \ (Q
1
∪ Q
2
). ¤
In order to evaluate this algorithm, we tested it
with the ontologies aeo and gio:
Example 3.7. After the ontology reuse, aeo contains
2473 axioms and gio 607. The current form of aeo
KEOD 2009 - International Conference on Knowledge Engineering and Ontology Development
418
ontology, has generalized only some of its concepts by
reusing external concepts from gio ontology. Thus, gio
ontology is not threatened by aeo. For the purpose of
this example, we added the following axioms to aeo:
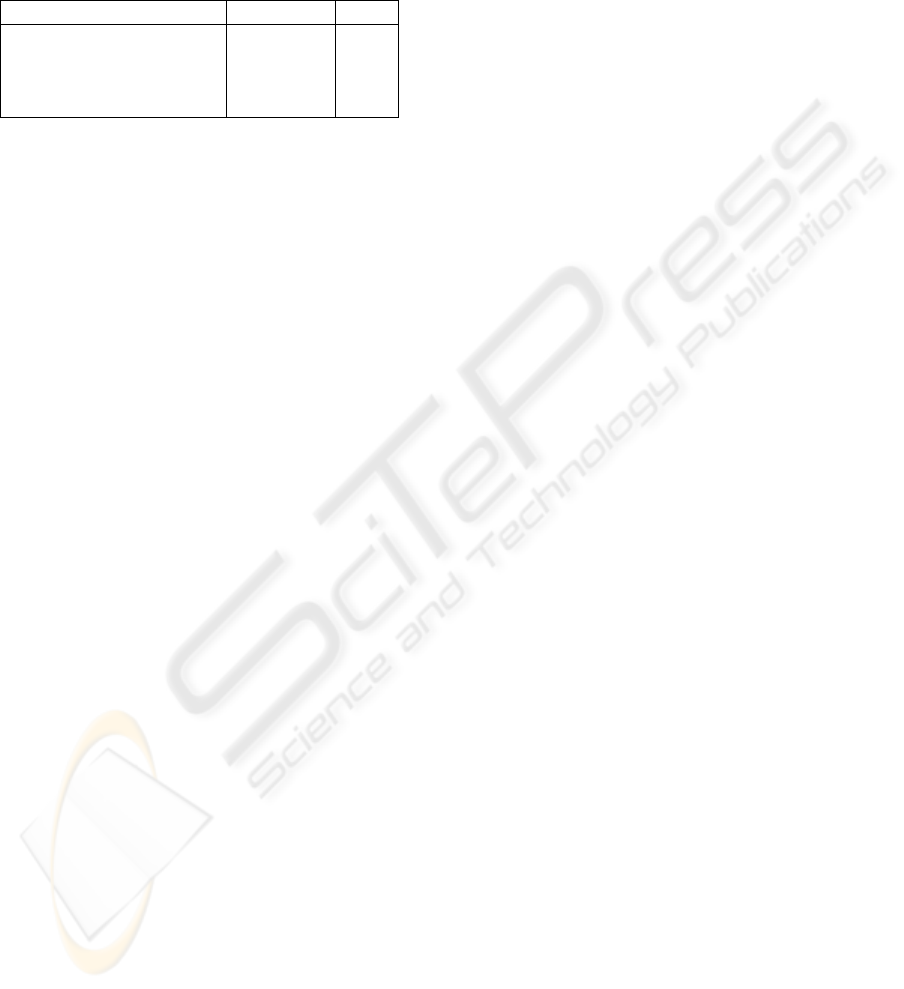
Table 1: Experimental results.
Axiom Thr. Ax. % Time
g:GeographicObject v HLC 33.4 7.06
g:Polygon v HLC 0 6.87
g:Surface v HLC 0.4 9.51
g:Building v ∃hasPart. MLC 2.6 7.79
The first column of the table demonstrates the ax-
ioms added, the second the percentage of gio ontology
threatened by the corresponding axiom and the third
the time (seconds) required to return the results.
The GeographicObject concept of gio ontology is
relatively high in the hierarchy and thus the potential
modification of its definition will affect a large part of
gio ontology. On the other hand, Polygon concept is
on the bottom of the ontology and thus does not affect
any part of gio ontology. Consequently, the user is al-
lowed to refine this concept, although other concepts
of gio have been generalized, without any change on
the information provided by gio. The Surface concept
affects the following axioms:
Polygon v Surface (8)
MultiSurface v ∃hasGeometryObject. Surface (9)
MultiPolygon v MultiSurface (10)
which were traced by our method (0,4% of the whole
ontology). The modification of the Building concept
threatens 16 other subconcepts of this concept.
4 RELATED WORK
Two basic directions define the research areas devel-
oped in the field of knowledge reuse. The first direc-
tion is concentrated on the safe ontology reuse. The
second direction is focused on the development of ap-
propriate formalisms that enable the ontology reuse
via conceptualized interpretations (Bao et al., 2007).
The research based on the first direction has lead
to the exploitation of the notion of module and the
development of tools like PRoSE, which enables the
safe ontology reuse but under very strict constraints
(the user is allowed only to generalise or to refine the
concepts of the target ontology). Another interesting
approach is suggested by (Suntisrivaraporn, 2008),
where a new kind of module is introduced, but it con-
cerns only E L+ ontologies.
5 CONCLUSIONS - FURTHER
RESEARCH
In this study we described a method by which we can
approximate the ontology reuse problem. After the
integration of two ontologies, the ontology designer
is informed about the extent of the loss of information
that will occur in order to maintain the safety state. In
this way, the designer can choose the appropriate on-
tology to reuse concepts from, based on the criterion
of causing the least loss of information.
For further research, we are interested in adjusting
the method in order to deal with more complex ax-
ioms than the simple axioms. We are also interested
in examining the condition of safety, in case the set of
refined entities belongs to a disjoint module from the
set of generalised entities. Finally, another direction
followed by our research could be to investigate the
ontology reuse problem in the case of interaction of
more than two ontologies.
REFERENCES
Baader, F., Calvanese, D., McGuinness, D. L., Nardi, D.,
and Patel-Schneider, P. F., editors (2003). The De-
scription Logic Handbook: Theory, Implementation,
and Applications. Cambridge University Press.
Bao, J., Slutzki, G., and Honavar, V. (2007). A semantic
importing approach to knowledge reuse from multiple
ontologies. In AAAI, pages 1304–1309.
Grau, B. C., Horrocks, I., Kazakov, Y., and Sattler, U.
(2007a). Extracting modules from ontologies: The-
ory and practice. Technical report, The University of
Manchester.
Grau, B. C., Horrocks, I., Kazakov, Y., and Sattler, U.
(2007b). Just the right amount: extracting modules
from ontologies. In WWW, pages 717–726.
Jim
´
enez-Ruiz, E., Grau, B. C., Sattler, U., Schneider, T.,
and Llavori, R. B. (2008). Safe and economic re-use
of ontologies: A logic-based methodology and tool
support. In ESWC, pages 185–199.
Lutz, C., Walther, D., and Wolter, F. (2007). Conservative
extensions in expressive description logics. In IJCAI,
pages 453–458.
Suntisrivaraporn, B. (2008). Module extraction and incre-
mental classification: A pragmatic approach for el+
ontologies. In ESWC, LNCS. Springer Verlag.
A METHOD FOR APPROXIMATION TO ONTOLOGY REUSE PROBLEM
419
