ONTOLOGY DESIGN THROUGH MODULAR REPOSITORIES

Ali Hashemi and Michael Gruninger

Semantic Technologies Laboratory, University of Toronto, 5 King’s College Circle, Toronto, Canada

Keywords:

Ontologies, Ontology design, Knowledge representation, Knowledge engineering.

Abstract:

Many real world problems require a language at least as expressive as ﬁrst order logic, yet there exist many

barriers to the generation of ﬁrst-order ontologies. One of the biggest hurdles is the speciﬁcation of axioms

that capture the intended semantics of a user’s concepts. This paper presents an ontology design algorithm

enabled by modular ontology repositories that consist of theories organized into disjoint hierarchies, each of

which is a set of nonconservative extensions. The ontology design algorithm provides axiomatizations of re-

lations by eliciting intended models from the users, identifying the strongest theories in the repository that

are satisﬁed by the intended models, and incorporating user feedback to verify the proposed set of axioms.

This approach emphasizes the communication of semantics rather than syntax via concrete examples, allow-

ing users to express intuitions about their domains without extensive background in the intricacies of formal

languages.

1 INTRODUCTION &

MOTIVATION

Many of the problems encountered in realistic appli-

cations require ontologies that are speciﬁed in a lan-

guage with at least ﬁrst-order expressivity. Never-

theless, ﬁrst-order logic poses signiﬁcant hurdles for

many subject matter experts. Few have the adequate

training or familiarity in ﬁrst-order logic to express

their ideas with facility in the language. The syn-

tax and grammar of most implementations of ﬁrst-

order logic may often appear unintuitive and un-

wieldy. Compounding these barriers is also a paucity

of guidelines and tools to support the generation of

axioms; no best practices exist to help designers for-

mulate axioms. Moreover, once expressed, it may be

difﬁcult to gauge the quality of the axioms.

Indeed, as Hou et al have noted, “research in clas-

sifying and representing axioms in a user-friendly

way has been relatively sparse in the knowledge-base

system community” (Hou et al., 2005). Several no-

table attempts have been made in this regard, both

attempting to develop patterns and templates for ax-

iom formulation based on existing ontologies (Hou

et al., 2005; Staab and Maedche, 2000). More re-

cent work has focused on identifying “design pat-

terns” which ontology designers may reuse (Presutti

and Gangemi, 2008). Yet these works focus on di-

rectly representing the axioms to user, for exam-

ple by translating logical axioms into English - i.e.

www.ontologydesignpatterns.org. This work differs

drastically as it focuses on communicating with the

ontology designer at the semantic level. In many

ﬁelds a domain expert might be more comfortable

specifying a relation via concrete positive and nega-

tive examples.

A versatile ontology design algorithm has been

developed which allows ontology designers to cir-

cumvent the problem of becoming intimately famil-

iar with a ﬁrst order logic language, instead allowing

them to focus on the semantics of what they wish to

represent. We do so by requiring only two things: (i)

that a domain expert be able to “draw” at least one

representation of a model for relation to be deﬁned;

(ii) the subject matter expert must be able to recognize

whether models of existing ontologies are acceptable

manifestations of their relation. This algorithm is en-

abled by incorporating two simple principles in the

design of an ontology repository, allowing the repos-

itory to function as a “map” of known theories. The

algorithm then traverses the repository to deliver the

most appropriate axioms to the ontology designers.

The algorithm rests on the relationship between

a theory and its model (in the Tarskian sense). The

word model as used throughout this paper, refers to

the set of objects in a domain of discourse which sat-

isfy the axioms. While in general, the correspondence

between a set of models and a set of axioms that are

192

Hashemi A. and Gruninger M. (2009).

ONTOLOGY DESIGN THROUGH MODULAR REPOSITORIES.

In Proceedings of the International Conference on Knowledge Engineering and Ontology Development, pages 192-199

DOI: 10.5220/0002299201920199

 SciTePress

satisﬁed by them are many to many, we address this

problem by exploiting properties of the accompany-

ing repository. This paper will begin by brieﬂy de-

scribing the essential components driving the algo-

rithm, followed by the strategy employed to capitalize

the relation between syntax and semantics. Next, the

basic principles of the supporting ontology repository

will be provided, followed by the ontology design al-

gorithm and a sketch of its correctness proof. A brief

use case will provide a concrete example of the algo-

rithm in action.

2 MODELS AND LOGICAL

STRUCTURE

We consider a formal ontology as in the sense pro-

vided in (Guarino, 1998). Namely, an ontology O

, is

a set of logical formulae in some language L that aim

to capture the intended models of a particular concep-

tualization C. A model for the ontology is constructed

via an interpretation I, assigning each element of the

vocabulary V to the extensional structure of the con-

ceptualization S = {D,R} and thus to either elements

of the domain D or the conceptual relations R (Guar-

ino, 1998).

The approach taken here is to bypass the syn-

tax and grammar of any particular formal language,

and instead let users specify concepts extensionally.

Particularly, if we focus our attention on the models

of any theory, we notice that they contain particular

structures. Take for example a Hasse diagram, which

is often used to represent models for partially ordered

sets. In these diagrams, nodes are taken to be ele-

ments from the domain of discourse, D and edges the

less-than-or-equal-to (leq) relation (from R). These

models implicitly capture the axioms which gener-

ated them; speciﬁcally, the way in which the edges

and nodes are constructed reﬂect the associated poset

axioms. While the mapping of nodes to say numbers,

and edges to leq is achieved via a particular interpre-

tation, the resultant model structures exist indepen-

dently of the interpretation which assigned them to

that conceptualization. Let us call this abstracted di-

agram a particular model structure (in this paper, we

use the term logical structure interchangeably) for a

theory. If we change our domain of discourse, the

axioms for posets could equally well apply to a par-

ticular notion of time, or some versions of mereology.

We exploit exactly this notion of model structure

to bypass the syntax of a formal language such as ﬁrst-

order logic and allow ontology designers to specify

a particular relation via communication at the model

representation level alone. Of course, there exists

in general a many-to-many mapping between mod-

els and theories. Figuring out how to properly make

the transition from a set of models to the appropriate

theory is more involved. Once we start collecting and

growing the acceptable models, the number of candi-

date theories is reduced. Moreover, by keeping track

of those models which we do not want, we identify

the unintended models. By collecting a coherent set

of models that we want, and a set of those we don’t

want, in the limit we might reach a one-to-one map-

ping between a theory and a set of models.

The above is the key to our algorithm - we try to

ﬁnd the best match between a theory in a given reposi-

tory and the set of (in)admissable models as identiﬁed

by an ontology designer. Since the set of intended

models, IM is not always immediately available, we

elicit a subset from the user, UM. As noted above, it is

not enough to jump from UM to a theory, T . Further

interaction is required in which the system provides

models SM of existing ontologies and the user identi-

ﬁes as either admissible or not. In this way we may

be more conﬁdent in going from a set of models to a

theory. There are a number of further nuances to this

approach which will be elaborated in the rest of the

paper.

3 REPOSITORY

Underlying the design algorithm of course is a modu-

lar ontology repository - this where candidate theories

are selected from (Luettich and Mossakowski, 2004).

Any repository satisfying the two basic principles dis-

cussed later in this section, allows a successful imple-

mentation of the algorithm (guarantees its correctness

proof). For ease of understanding and concreteness,

in this paper we present a particular repository design

using the Common Logic Interchange Format (CLIF)

(Delugach, 2007).

Any such repository should extend along two di-

mensions: one which we call Abstraction Layers and

the other Core Hierarchies. Abstraction layers serve

to signiﬁcantly reduce conceptual clutter and help bet-

ter delineate the types of theories being discussed;

moreover they are essential in helping satisfy the sec-

ond repository design criterion. Core Hierarchies

gather theories as a map which the algorithm tra-

verses.

3.1 Abstraction Layers

The repository serves as a sort of inverted upper on-

tology, since users are plugging in not necessarily to

reuse concepts such as time and space, but to reuse

ONTOLOGY DESIGN THROUGH MODULAR REPOSITORIES

193

the model structures of their underlying logical theo-

ries. In our example repository, we decided that math-

ematical theories corresponded to the lowest level of

abstraction.

Theories formalizing the notions of orderings,

groups, ﬁelds, geometries characterize a large family

of logical and model structures that recur frequently

in many applications. These theories form our base

abstraction layer. Our next Abstraction Layer con-

sists of theories from the traditional domain of upper

ontologies - formalizing notions such as Space, Time,

Mereotopology etc. Note that many of these concepts

actually reuse logical structures from the base mathe-

matical layer. Moving upwards thusly, we add layers

which characterize more and more specialized con-

cepts (say agents, or processes etc.)

The layers are connected to one another either via

representation theorems or mapping axioms. Discus-

sion of these links are outside the scope of this paper.

For the purposes of the algorithm, it sufﬁces to say

that a repository ought be organized via some sort of

abstraction layers, as each abstraction layer consists

of Core Hierarchies, which drive the design process.

3.2 Core Hierarchies

As noted above, each layer is populated by a num-

ber of Core Hierarchies. A Core Hierarchy is a col-

lection of modules (theories or set of axioms), which

non-conservatively extend a conceptual domain. For

example, the notion of a partial order may be non-

conservatively extended in numerous ways from poset

(one module) to lattice (another module) to Boolean

lattice (yet another module). Of course, a repository

may consist of more than one core hierarchy - thus our

Abstraction Layer for mathematical theories consist

of separate hierarchies for posets, geometries, groups,

symmetries, ﬁelds etc.

The stipulation here that any compliant repository

must satisfy is that no Core Hierarchies at the same

level of abstraction may share a non-conservative ex-

tension with one another. If there exists a mod-

ule within an abstraction layer which is a non-

conservative extension of two hierarchies, then it sug-

gests that the two hierarchies should in fact be com-

bined as one.

In comparing two theories or modules in a core

hierarchy from the repository, we may also say that

one is stronger than another as follows. Given module

A and B, if A is a non-conservative extension of B,

then A is stronger than B by virtue of the fact that

more theorems may be proven.

To recap, there were two requirements for any

repository (modularity is taken as a given). First,

modules should be linked in such a way as to form

a Core Hierarchy, with the caveat of no shared non-

conservative extensions at the same abstraction level.

Following from this restriction, is that the repository

should incorporate the notion of abstraction layer (the

speciﬁc ordering of layers is left to the repository de-

signer).

4 ALGORITHM

Now that the basic reference point from which theo-

ries will be selected has been exposited, we shall de-

scribe how such a repository may be leveraged. The

algorithm consists of two parts, (i) elicitation of user

models and (ii) the proposal of models for existing

ontologies (see Figure 1.

The ﬁrst component locates the user somewhere in

the repository, providing “bounds” for theories which

characterize the user’s intended models. Models de-

rived from existing ontologies in the repository, cou-

pled with user responses, tighten this bound, eventu-

ally selecting the strongest (if any) theories from the

repository which capture the user’s intuition. The fol-

lowing sections will elaborate each component.

4.1 Elicitation of User Models

Acquiring user models necessitates that there exist a

suitable representation for models of the concept or

relation under consideration. Such a representation is

not always obvious or available. However, any repre-

sentation of a model is suitable so long as we are able

to unambiguously and repeatedly generate a complete

diagram (the set of all positive and negative literals)

from the depiction. Consider again a Hasse diagram -

there are certain conventions for interpreting the dia-

gram - namely that edges are transitive and ordered

spatially. So long as these conventions are explic-

itly communicated and understood, we may always

generate the same complete diagram from a particu-

lar Hasse diagram, as in Figure 5.

The elicitation of models need not be restricted to

Hasse diagrams, indeed changing the conventions of

graph depictions might allow one to specify a model

for a non-transitive relation. Alternatively, an audi-

tory or tactile model depiction may be more natu-

ral for certain domains. For our proof of concept,

we developed a simple piece of software allowing a

user to specify binary relations using graphs. Users

could also explicitly modify conventions for convert-

ing graphs into complete diagrams. Once a complete

diagram for a model is generated, we identify which

theories the model satisﬁes. In this way, we locate the

KEOD 2009 - International Conference on Knowledge Engineering and Ontology Development

194

Inputs:

• At least one user generated model that is inter-

pretable by the ontology design tool.

• Yes or no answers by the user to the models se-

lected by the design tool

Outputs: The set of strongest axioms with respect

to the repository that is consistent with the user’s un-

derstanding as determined by the sets of accepted and

rejected models.

1. Elicit-Models

2. Select-Models

Figure 1: The Algorithm Axiom-Generation.

initial candidate theories which may characterize the

user’s intended models.

4.2 Initializing in the Repository

To begin the algorithm, we require at least one (or

more) user model, which is independently tested

against theories in a single core hierarchy via a

breadth-ﬁrst specialization search

. We begin with

the most general module, see if it is satisﬁed by the

model, then move on to its children. If a particular

theory is not satisﬁed, then it and all its children are

pruned from the search tree. Moreover, since the hier-

archies share no non-conservative extensions, we may

explore them independently. We make use of an au-

tomated theorem prover or a satisﬁability checker to

verify that the provided models satisfy the theories.

We may then compare the theories which were

satisﬁed by each user model. If no core-hierarchy

had at least one theory which was satisﬁed by all

user models, then the algorithm terminates - either the

user is trying to formalize inconsistent models, or the

repository has insufﬁcient breadth. On the other hand,

if there is at least one module in some core hierarchy

which is satisﬁed by all models, then we may proceed

to the second phase of the algorithm. We present here

the algorithm in parts; while the steps are distributed

through the text, they comprise a single algorithm.

The steps in Figure 2 ﬁrst collect all the mod-

ules in hierarchy j satisﬁed by user model i in

Consistent UM

i, j

. We take its intersection and rid all

the parents to yield the strongest theories in hierar-

We will use the following terminology: CH

m, j

denotes

module m in hierarchy j, UM

denotes user model i, Above

is the set of all modules connected to and directly above

theory K, and Below

is the set of all modules connected to

and directly below theory K.

1. Let UM = UM

the set of all models generated by

user

2. Breadth-First Specialization Search: If CH

m, j

is satisﬁed by UM

, then add CH

m, j

Consistent UM

i, j

3. Termination Condition:

(a) If for any U M

every Consistent UM

is empty,

then End Algorithm.

(b) If for any j, the intersection of all

Consistent UM

i, j

is empty, then End Al-

gorithm.

4. Initialize: Let Consistent

Consistent UM

i, j

5. Rid Parents: For every element CH

m, j

∈

Consistent

if its child is in Consistent

then re-

move CH

m, j

from Consistent

Figure 2: The Algorithm Elicit-Models.

chy j that are consistent with all the user models in

Consistent

. This set serves as the lower bound of

candidate theories, the upper bound is simply the root

of the hierarchy. We have thus located the user in the

repository and passed the initiative to the software.

One problem with trying to derive an underlying

theory by examining extensional models is that the

models might exhibit accidental properties. For ex-

ample, if asked to draw a triangle, many will inad-

vertently draw an equilateral or isosceles triangle. To

account for this condition, we must explore more gen-

eral theories and see if a model of them is acceptable

to the user. If so, then the weaker theory is appropri-

ate.

4.3 Select Models

Once user models have been mapped to the hierar-

chy, there are two scenarios: either there is a unique

lower bound or there are multiple candidate theories.

If unique, the algorithm proceeds to the Generalize

step in Figure 4 below. If not, the algorithm takes the

join of the strongest theories, T

, selects a model for it

and presents it to the user. If the user ﬁnds the model

acceptable, we proceed again to Generalize. If not,

the algorithm constructs all possible chains from each

strongest theory to T

In this case, we know that the theories the user de-

sires are bounded by T

above and Consistent

below.

We traverse each chain from the most general theo-

ries (top down) showing models for each module. If

accepted, we terminate exploration of that chain and

ONTOLOGY DESIGN THROUGH MODULAR REPOSITORIES

195

store T

test

in Proposed

. Otherwise, we iteratively re-

move the top element till there is only one element left

in the chain. At this point, we test if the union of the

selected models in each chain is consistent. If so, we

have developed the strongest axioms from this hierar-

chy for the user, otherwise the algorithm terminates.

We then move to the component of the algorithm for

combining results from the various hierarchies.

If the resultant theories are not mutually consis-

tent, the algorithm terminates. The reason for this

apparent inconsistency in the user responses may be

that the user is trying to deﬁne a relation over multiple

sorts simultaneously. Alternatively, they may desire a

theory not in the repository. Since these cases cannot

be disambiguated, the algorithm simply exits.

Figure 3: The relation between modules (theories) and their

associated sets of models. Moving rightwards, we have

non-conservative extensions.

In the case where Consistent

consisted of a

unique theory in a core hierarchy, then instead of the

chain method, we look directly at the theories above

and below the initialized theory. The hierarchy func-

tions as a “map” which the algorithm navigates, pro-

pelled by user responses to proposed models. Imagine

the user is situated at T

with models “above” and “be-

low” as in Figure 3, then the following algorithm ap-

plies. To ensure that T

is the desired theory, we must

exhaust the search space by constructing models for

those above and combinations of those below. As be-

fore, to account for inadvertent properties in the set of

user models, we need to test the weaker theories. We

may do this by negating T

and constructing a model

for each T

. If any of these models are accepted, we

know that a more general theory is required, and we

reset T

to one of those above.

If we can no longer generalize, then we look to

prune those below T

. We may construct as many

models corresponding to those areas in M

above. In

this case, we learn through rejection. If these mod-

els are accepted, then the proposed axioms do not

change. A rejection however, results in the addition

of ¬T

to the proposed axioms. In this process, as

illustrated in the steps below, we may ensure that the

strongest axioms from core hierarchy j are selected.

These steps are reﬂected in Figure 4.

Up to the Combine Hierarchies steps, we have

selected the strongest theories for the user’s intended

models from a single hierarchy. Of course, it may

have been the case that the user models satisﬁed the-

ories in more than one hierarchy. The algorithm up to

this point repeats for each core hierarchy which had

at least one theory which were satisﬁed by all the user

models, now we must combine the results.

For each core hierarchy j, which provided full

cover the user models, we now have the set H

0, j

which

are the strongest theories. We recall that our initial

stipulation was that each Core Hierarchy not share

a non-conservative extension with another. Conse-

quently, we need only check if the union of all H

0, j

is consistent. If so, we have determined the strongest

axioms that are consistent with all user models, all

those denoted accepted and inconsistent which those

marked reject. Otherwise, the algorithm terminates

due to possibly conﬂicting inputs by the user.

4.4 Theorem and Correctness Proof

Given user inputs and a modular repository, the cor-

rectness of the algorithm is characterized by the fol-

lowing theorem:

Theorem 1. The algorithm Axiom-Generation gen-

erates a set of the strongest theories H

that satisfy

the following properties:

1. H

is a composite of the theories from the ontology

repository

2. H

is consistent with all user generated models.

3. H

is consistent with all selected models that the

user denoted Accept

4. H

is inconsistent with all selected models that the

user denoted Reject

The full correctness is too long for this paper, here

we only provide a sketch. We ﬁrst need to prove four

lemmata, the ﬁrst (lemma 1) showing that the algo-

rithm applies i.e. ensuring that there is at least one

theorem in some core hierarchy that satisﬁes all the

user models. If such a theory exists, then the algo-

rithm may continue, otherwise it terminates as shown

in Figure 2 above. Lemma 2 establishes that for

each core hierarchy, the algorithm initializes at the

strongest theories which are satisﬁed by all the user

models. Brieﬂy, using lemma 1, we can show this is

achieved by the Rid Parents sub process.

Lemma 3 shows that for each investigable core hi-

erarchy, we may attain a set of theories H

0, j

which are

KEOD 2009 - International Conference on Knowledge Engineering and Ontology Development

196

1. For every hierarchy, where |Consistent

| > 0

2. If |Consistent

| > 1 and user rejects M

(where

is a model selected for T

(CH

m, j

∈

Consistent

))

(a) Construct all chains, Chain(T

, A), where A ∈

Consistent

(b) For each chain, create M

Ttop

for T

top

(top of

chain k)

i. If M

Ttop

is accepted, M

Ttop

∈ Accept

, end

chain, add T

top

to Propose

ii. If M

Ttop

is rejected, M

Ttop

∈ Re ject

, remove

top element of chain, T

top

is now new top ele-

ment of chain. If top=bottom, end chain, add

top

to Propose

i. If Propose

is not consistent End Algorithm

ii. If Propose

is consistent, check next hierar-

chy, otherwise, goto Combine Hierarchies

Generalize

3. Set T

= Consistent

4. For each A

∈ Above

, Construct M

from

¬Below

(a) If M

is rejected, then remove A

from

Above

and M

∈ Re ject

(b) If M

is accepted, then M

∈ Accept

and set

= A

, generate new Above

Specialize

5. Construct M

∗ from T

∗ = T

¬Below

(a) If accepted, M

To∗

∈ Accept

(b) If rejected, M

To∗

∈ Below

and Propose

Below

6. For every B

∈ Below

o Construct M

∗ where

∗ = B

¬(Below

)

(a) If accepted, M

∗ ∈ Accept

try next B

(b) If rejected, M

∗ ∈ Re ject

, add ¬B

Propose

7. H

0, j

Propose

8. Combine Hierarchies

(a) Let Combine =

0, j

(b) If Combine is consistent, then display: “The

strongest set of axioms from the repository

which correspond to your inputs are Combine”

End Algorithm

Figure 4: The Algorithm Generalize-Models.

the strongest theories in that hierarchy that are consis-

tent with all the elements of Accept

and inconsistent

with all elements of Re ject

. Finally, lemma 4 ensures

that the set Combine is the union of the strongest theo-

ries from the repository that are consistent with every

and inconsistent with every Re ject

With these lemmata, we may prove the correctness

theorem, since by lemma 1 we know the algorithm

engages only if there is a hierarchy in the repository

which satisﬁes all the user models (hence satisfying

property 1 and 2). Lemma 2 shows that we can always

select the strongest theories in a core hierarchy, while

lemma 3 shows that these theories will be consistent

with Accept

and inconsistent with Re ject

. Finally,

lemma 4 shows that we may extend this result to all

Accept and Reject sets, otherwise the algorithm termi-

nates. Combining these results satisﬁes the ﬁnal two

properties of the theorem.

5 USE CASE

In this section we will brieﬂy show how this algo-

rithm would apply for a real world concept. We

take as given the existence of an ontology for par-

tially ordered sets organized as a core hierarchy. We

aim to add axioms to the ﬂows relation from SUMO,

which aside from categorization axioms, only asserts

its anti-symmetry and transitivity (Nichols, 2004).

User models have been constructed by looking at

a map and selecting rivers as nodes and edges as the

ﬂows relation. Figure 5 illustrates two such depictions

of models for ﬂows. Each model is converted into a

complete diagram and tested against the poset hierar-

chy to see which theories are satisﬁed by them.

Axioms for posets, comparability graphs, down

forests and down trees are all satisﬁed by these mod-

els. However we initialize only at down tree since all

the other theories have children in Consistent

. Since

we have a unique theory as the current lower bound,

we do not invoke the chain investigation and instead

try to generalize and then specialize.

In this case, Above

downtree

= {Down Forest,

Bounded Meet Semi Lattice}. The algorithm selects a

model for each that is not a down tree. The ﬁrst model

proposed is a series of down trees (a down forest). As

we are acting as the user in this case, our understand-

ing is that most uses of ﬂow have every river or body

of water ﬂowing into a unique body of water.

Hence,

we reject this model.

The next model is that of a bounded meet semi lat-

tice that is not a down tree (i.e. a child may have more

not necessarily so, but assumed for this use case

ONTOLOGY DESIGN THROUGH MODULAR REPOSITORIES

197

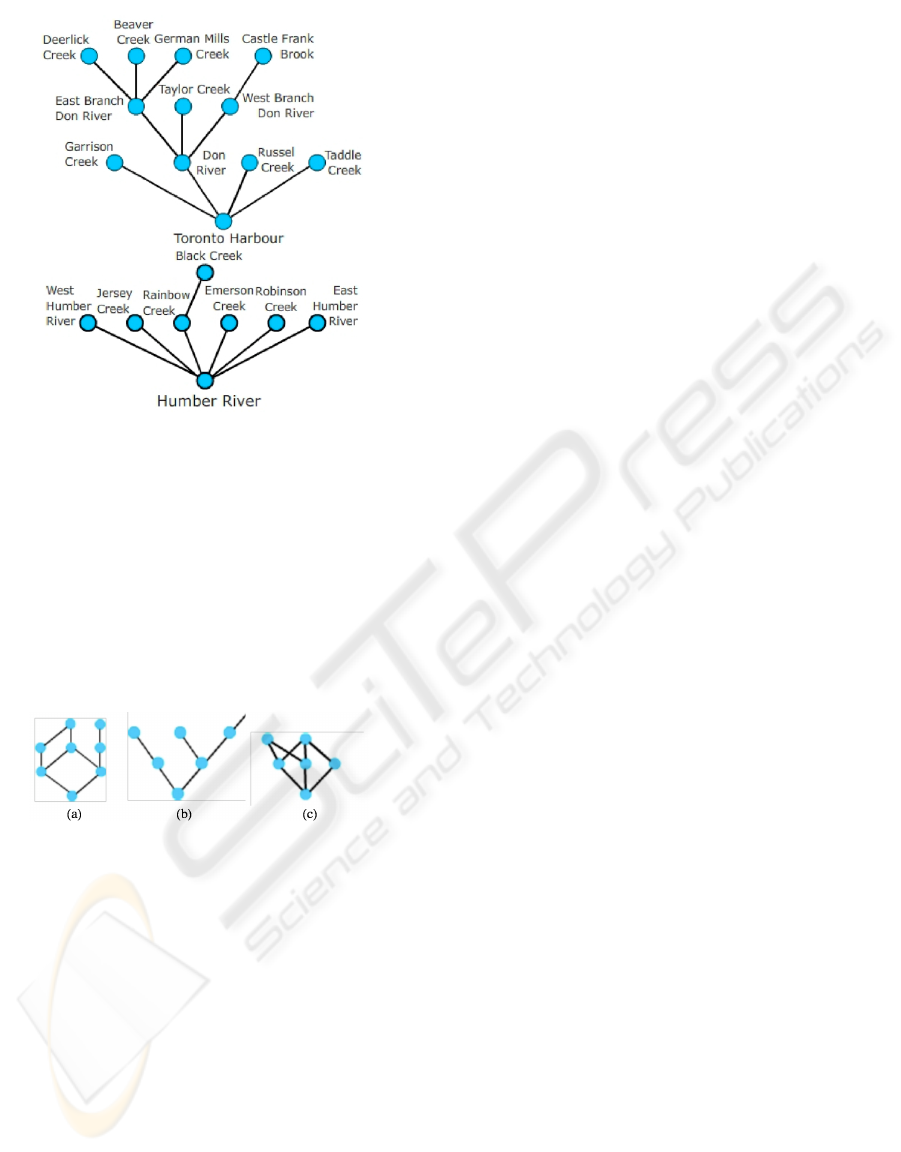
Figure 5: Hasse diagram conventions for two user models.

Nodes are names of rivers, edges are the ﬂows relation.

than one parent). This seems acceptable since rivers

may bifurcate then join up again, so it is accepted.

The algorithm now has a new T

, namely, bounded

meet semi lattice. We create a new Above

o = poset

in this case and again, we the present the user with a

model for a poset which is not a bounded meet semi

lattice. This model is rejected because it admits rivers

ultimately ﬂowing into more than one body of water.

Figure 6: Several software proposed models: (a) uniquely a

bounded meet semi lattice; (b) down tree; (c) bounded meet

semi lattice that is not a down tree.

We now try to “Prune Specialize” by investigating

Below

= {Down Tree, Meet Semi Distributive Lat-

tice, Meet Pseudo-complemented Lattice, Meet Semi

Modular Lattice}. The ﬁrst model presented is thus a

uniquely bounded meet semi lattice that does not ex-

hibit the properties of any of its children. This seems

plausible so we click accept. Next, the algorithm se-

lects a model which satisﬁes each element of Below

exclusively. Every model seems like a potential mod-

els of rivers ﬂowing into one another, so we accept

each and they are all added to Accept

. As there are

no other combinations to try, nor other core hierar-

chies to investigate, we have H

= H

0, j

= Propose

{Bounded-Meet-Semi-Lattice} and Accept

is the set

of all the user models plus those we accepted, while

Re ject

is the set of all the rejected models. We note

that the axioms for bounded meet semi lattice were

satisﬁed by all the models in Accept

and not by those

in Re ject

. Thus we have provided axioms for ﬂows

by reusing axioms for leq as constrained by the theory

for bounded meet semi lattices.

6 DISCUSSION

In this paper we have presented two basic design prin-

ciples for any ontology repository which enables an

ontology design algorithm. The algorithm uses the

repository as a “map” of theories through which it

navigates to identify the most appropriate character-

ization of the user’s intended models.

It relies on the structure of the repository and the

nature of non-conservative extensions. User models

initialize the algorithm within one or more core hier-

archies in a single abstraction layer. The algorithm

then tries to determine whether there were acciden-

tal properties in the user models by exploring weaker,

more general theories. It does so by proposing mod-

els which do not exhibit the stronger qualities. Once

these have been exhausted, the algorithm attempts to

identify the strongest possible theories, by exploring

the set of modules below the selected theory. The al-

gorithm uses falsiﬁcation to drive its navigation of the

repository. It selects models based on the interesting

areas as shown in Figure 3. Each region in the “model

space” is an interesting one which is accounted for

and tested by the algorithm.

In its current guise, the algorithm only formalizes

one relation at a time. A Sandbox Tool has been de-

veloped for graphs, which allows users to depict mod-

els for binary relations while explicitly specifying the

translation conventions. Again, given adequate speci-

ﬁcation, a non-alpha numeric representation may be

converted into a complete diagram for a model, in

any sensory arrangement. The only restriction is that

such depictions must have a clear, unambiguous and

repeatable translation into complete diagrams. This

process is suited for relations with arity of 2-5 - any

higher and it becomes difﬁcult to ﬁnd a suitable repre-

sentation for the models. Some relations with higher

valence may be projected into a smaller dimension

given a contextual framing.

The precision and accuracy of the proposed ax-

ioms of the algorithm are dependent on the breadth

and depth of the reference repository. There may al-

ways be some additional axioms which the designer

wishes but are not present in the repository. While

the algorithm is necessarily silent about these axioms,

should they be formalized, the repository can grow to

KEOD 2009 - International Conference on Knowledge Engineering and Ontology Development

198

accommodate these novel learnings.

The algorithm relies on a theorem prover and/or

satisﬁability checker to verify that a particular model

indeed satisﬁes the axioms of an ontology. It is im-

portant to realize that the algorithm is not dynami-

cally constructing new models of the axioms (which

in general is undecidable). Since the repository is a

(relatively) static entity and we know which theories

are above and below any other theory, we can con-

struct all the necessary models before engaging the

algorithm. We need only convert the diagrams into

the desired representation convention on the ﬂy.

7 CONCLUSIONS

The work presented here only scratches the surface of

a novel way of axiom generation - that of conversing

at the semantic level. It greatly reduces the burden on

subject matter experts to intimately learn a formal lan-

guage. Moreover, it skirts many of the issues of Up-

per Ontologies by not taking positions on the nature

of “reality,” but by capturing the logical structures that

underlie many concepts. Consequently, user concepts

do not necessarily map into particular conceptualiza-

tions of space and time, but rather the more abstract

concepts of “properties of binary (or higher arity) re-

lations.”

Moreover, as interrelations between layers of ab-

stractions become formalized, more natural model

representations might also be used. For example

a molecular biologist might be able to draw mod-

els based on actual molecules instead of abstracted

graphs. Similar to how users can customize skins for

software graphical user interfaces, model representa-

tions may be skinned, so as to reﬂect a representation

more natural to a subject matter expert’s domain (i.e.

a molecular biologist might look at spatial conﬁgura-

tions of molecules.)

Closely related, are questions of representing high

arity relations, or models of inﬁnite size. Contexts

and/or project may address the former, while ellipses

and/or navigable fractals may be promising depic-

tions. Explicit conventions would mitigate some of

these issues, but these ideas are preliminary at the mo-

ment.

Similarly, we currently axiomatize structures that

are isomorphic to the extensions of a single relation.

Extending this work to multiple relations presents an

interesting challenge. How does the interaction of re-

lations affect which models to propose?

Lastly, an extension to the repository would see

it retain the relation names when a user engages the

algorithm to axiomatize a relation. In this way, we

might be able to enrich the user browse experience by

presenting different, previously user deﬁned notions

of say, time. One could then compare time as deﬁned

by A vs. B and see whether either of those deﬁnitions

corresponds to the time they wish to axiomatize.

In this paper we have shown how the organiza-

tion of theories within an ontology repository can be

exploited to provide an axiomatization of a class of

models. Furthermore, such a repository structure pro-

vides the foundation for many other applications in

ontological engineering. One such example is an al-

gorithm for the generation of semantic mappings for

ontologies consistent with those in the repository - the

repository serves as a central family of interlingua on-

tologies through which alignment may be achieved.

REFERENCES

Delugach, H. (2007). Common logic (cl) - a framework for

a family of logic-based languages. Technical report,

Geneva.

Guarino, N. (1998). Formal ontologies and information sys-

tems. In Formal Ontology in Information Systems.

Proceedings of FOIS’98, pages 3–15. IOS Press.

Hou, C. J., Musen, M., and Noy, N. F. (May 2005). Ez-

pal: environment for composing constraint axioms

by instantiating templates. International Journal of

Human-Computer Studies, 62:578 596.

Luettich, K. and Mossakowski, T. (2004). Speciﬁcation of

ontologies in casl. In Formal Ontology in Informa-

tion Systems Proceedings of the Third International

Conference (FOIS-2004), pages 140–150. IOS Press.

Nichols, D. (2004). Ontology of geography.

http://sigmakee.cvs.sourceforge.net/*checkout*/sigma-

kee/KBs/Geography.kif.

Presutti, V. and Gangemi, A. (2008). Content ontology de-

sign patterns as practical building blocks for web on-

tologies. In 27th International Conference on Con-

ceptual Modeling, pages 128–141. Springer.

Staab, S. and Maedche, A. (2000). Ontology engineer-

ing beyond the modeling of concepts and relations.

In 14th European Conference on Artiﬁcial Intelli-

gence; Workshop on Applications of Ontologies and

Problem-Solving Methods.

ONTOLOGY DESIGN THROUGH MODULAR REPOSITORIES

199