AN IMPROVED FREQUENT PATTERN-GROWTH APPROACH TO

DISCOVER RARE ASSOCIATION RULES

R. Uday Kiran and P. Krishna Reddy

International Institute of Information Technology-Hyderabad, Hyderabad, Andhra Pradesh, India

Keywords:

Data mining, Rare knowledge patterns, Rare association rules, Frequent patterns.

Abstract:

In this paper we have proposed an improved approach to extract rare association rules. The association rules

which involve rare items are called rare association rules. Mining rare association rules is difﬁcult with sin-

gle minimum support (minsup) based approaches like Apriori and FP-growth as they suffer from “rare item

problem” dilemma. At high minsup, frequent patterns involving rare items will be missed and at low minsup,

the number of frequent patterns explodes. To address “rare item problem”, efforts have been made in the lit-

erature by extending the “multiple minimum support” framework to both Apriori and FP-growth approaches.

The approaches proposed by extending “multiple minimum support” framework to Apriori require multiple

scans on the dataset and generate huge number of candidate patterns. The approach proposed by extending the

“multiple minimum support” framework to FP-growth is relatively efﬁcient than Apriori based approaches,

but suffers from performance problems. In this paper, we have proposed an improved multiple minimum sup-

port based FP-growth approach by exploiting the notions such as “least minimum support” and “infrequent

leaf node pruning”. Experimental results on both synthetic and real world datasets show that the proposed

approach improves the performance over existing approaches.

1 INTRODUCTION

Data mining represents techniques for discovering

knowledge patterns hidden in large databases. Several

data mining approaches are being used to extract in-

teresting knowledge (G. Melli and Kitts, 2006). Like,

association rule mining techniques (R. Agrawal and

Swami, 1993) (Agrawal and Srikanth, 1994) discover

association between the entities, clustering techniques

(Xu, 2005) to group the unlabeled data into clusters

such that there exists high inter similarity and low in-

tra similarity between the clusters, classiﬁcation tech-

niques (Weiss and Kulikowski, 1991) to identify the

different classes existing in categorical labeled data.

It can be observed that most of the data min-

ing approaches discover the knowledge pertaining to

frequently occurring entities. However, real-world

datasets are mostly non-uniform in nature contain-

ing both frequent and relatively infrequent or rarely

occurring entities. (Referring an entity as either fre-

quent or rare is a subjective matter depending on the

user and/or type of application etc.) In literature, it

has been reported that rare knowledge patterns i.e.,

knowledge pertaining to rare entities may contain in-

teresting knowledge useful in decision making pro-

cess (Weiss, 2004) (B. Liu and Ma, 1999). The rare

knowledge patterns are more difﬁcult to detect be-

cause they present in fewer data cases. In the litera-

ture, research efforts are being made to investigate ef-

ﬁcient approaches to extract rare knowledge patterns

like rare association rules and rare class identiﬁcation

(Weiss, 2004).

In this paper, we have proposed an improved ap-

proach to extract rare association rules. Association

rule mining (Agrawal and Srikanth, 1994) is a popular

knowledge discovery technique and has been exten-

sively studied in (J. Hipp and Nakhaeizadeh, 2000).

The basic model of association rule mining is as fol-

lows. Let I = {i

, i

, ..., i

} be a set of items. Let

T be a set of transactions (dataset), where each trans-

action t is a set of items such that t ⊆ I. A pattern

(or an itemset) X is a set of items {i

, i

, ..., i

} (1≤

k ≤ n) such that X ⊆ I. Pattern containing k num-

ber of items is called k-pattern. An association rule

is an implication of the form, A ⇒ B, where A ⊂ I,

B ⊂ I and A ∩ B =

0. The rule A ⇒ B holds in T

with support s, if s% of the transactions in T contain

A ∪ B. Similarly rule A ⇒ B holds in T with con-

Uday Kiran R. and Krishna Reddy P. (2009).

AN IMPROVED FREQUENT PATTERN-GROWTH APPROACH TO DISCOVER RARE ASSOCIATION RULES.

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval, pages 43-52

DOI: 10.5220/0002299600430052

 SciTePress

ﬁdence c, if c% of transactions in T that support A

also support B. Given T, the objective of association

rule mining is to discover all association rules that

have support and conﬁdence greater than the user-

speciﬁed minimum support (minsup) and minimum

conﬁdence (minconf). The patterns which satisfy the

minsup value are called frequent patterns. The rules

that satisfy the minsup value and minconf value are

called strong rules.

Rare association rule refers to an association rule

forming between frequent and rare items or among

rare items. Rare associations may contain useful

knowledge. For example, consider the set of items

{bread, jam, bed, pillow} being sold in a super mar-

ket. It can be observed that the items in the set {bread,

jam} are frequently purchased items while the items

in the set {bed, pillow} are infrequently or rarely pur-

chased items. Even though {bed, pillow} contains

rare items, it is interesting as it may generate more

revenue in this case.

Mining rare association rules is an issue, because

single minimum support (minsup) based approaches

like Apriori (Agrawal and Srikanth, 1994) and FP-

growth (H. Jiawei and Runying, 2004) suffer from

“rare item problem” dilemma (Mannila, 1997). That

is, at high minsup value, frequent patterns involving

rare items could not be extracted as rare items fail to

satisfy the minsup value. To facilitate participation of

rare items in generating frequent patterns, the minsup

value has to be set low. However, low minsup may

result in combinatorial explosion of frequent patterns.

To address “rare item problem”, efforts have been

made in the literature by extending the “multiple min-

imum support” framework to both Apriori and FP-

growth approaches. In this framework, each item is

speciﬁed a minsup value called minimum item sup-

port (MIS) and frequent patterns are discovered if a

pattern satisﬁes the lowest MIS value of an item in it.

The approaches (B. Liu and Ma, 1999) (Kiran and

Reddy, 2009) proposed by extending “multiple mini-

mum support” framework to Apriori require multiple

scans on the dataset and generate huge number of can-

didate patterns.

In (Ya-Han Hu, 2004) an approach called Condi-

tional Frequent Pattern-growth (CFP-growth) is pro-

posed by extending the “multiple minimum support”

framework to FP-growth. In this approach the MIS

value of each item is used to construct MIS-tree in-

stead of FP-tree. From the MIS-tree, compact MIS-

tree is derived with the items having support values

greater than the lowest MIS value among all items in

transaction dataset (the details are discussed in Sec-

tion 2).

The CFP-growth approach improves performance

over Apriori based approaches. However, it suffers

from performance problems. To generate frequent

patterns involving rare items, it carries out computa-

tion involving those items which do not generate any

frequent patterns. In this paper, we propose an im-

proved CFP-growth approach referred as Improved

Conditional Frequent Pattern-growth (ICFP-growth)

approach by exploiting the notions such as “least min-

imum support” and “infrequent leaf node pruning”.

The notion “least minimum support” is used to con-

sider only those items which generate frequent pat-

terns and the notion “infrequent leaf node pruning” is

used to prune the leaf nodes belonging to infrequent

items, so that the size of compact MIS-tree can be

reduced. Experimental results on both synthetic and

real world datasets show that the proposed approach

improves the performance over CFP-growth.

The paper is organized as follows. In Section

2, we discuss the mining of frequent patterns using

CFP-growth approach. In Section 3, we present the

proposed ICFP-growth approach and the algorithm to

mine frequent patterns. In Section 4, we present the

experiment results conducted on synthetic and real

world datasets. In the last section we discuss con-

clusions and future work.

2 CFP-GROWTH APPROACH

We ﬁrst deﬁne the terms “minimum item support”

and “sorted closure property”. Next, we brieﬂy

explain the CFP-growth approach along with the

performance problem.

Minimum Item Support. In multiple minimum sup-

port based frequent pattern mining, each item is spec-

iﬁed with a minsup value called minimum item sup-

port (MIS). Frequent items are the items having sup-

port greater than or equal to their respective MIS val-

ues. Infrequent items are the items having support

less than their respective MIS values.

Frequent pattern is a pattern that satisﬁes the low-

est MIS value of the item in it. (See Equation 1.)

S(i

, i

, ..., i

) ≥ min



MIS(i

), MIS(i

)

..., MIS(i

)



(1)

where S(i

, i

, ···, i

) represents the support for an

itemset {i

, i

, ···, i

} and MIS(i

) represents the

minimum item support for item i

Sorted Closure Property. The frequent patterns dis-

covered using multiple minsup values follow “sorted

closure property”. The “sorted closure property”

says, if a sorted k-pattern h i

, i

, ..., i

i, for k ≥

KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval

2 and MIS(i

) ≥ MIS(i

) ≥ ... ≥ MIS(i

), is frequent,

then all of its subsets involving item having lowest

MIS value (i

) need to be frequent and the subsets in-

volving rest of the items i

, where j ≥ 2, need not nec-

essarly be frequent patterns. So the multiple minsup

based frequent pattern mining algorithms have to con-

sider both frequent and infrequent items (complete set

of items I) to generate further frequent patterns.

For example, consider a transaction dataset in-

volving three items i

, i

and i

, each having MIS

values 5%, 10% and 20% respectively. If a sorted 3-

pattern {i

, i

} has support 6% then it is a frequent

pattern. In this frequent pattern, the supersets of item

i.e., {{i

}, {i

, i

}, {i

, i

}} are to be frequent.

However, the supersets of items i

and i

, say {i

, i

}

may still be infrequent by having support as 8%. For

this pattern to be frequent, the support it should have

is 10% (min(10%, 20%)).

The CFP-growth approach extends “pattern-

growth” methodology to multiple minimum support

values.

In this approach, it is assumed that the information

regarding the MIS values for the items will be the pro-

vided by the user prior to its execution. The MIS-tree

is constructed as follows. First, the items are sorted in

descending order of their MIS values, say L

and their

frequency values are set at zero. Next, a root node of

the tree is constructed by labeling with ”null”. Next,

for each transaction in the dataset the following steps

are performed to generate MIS-tree. They are:

1. The items in each transaction are sorted in L

or-

der. Next, update the frequencies of the items

which are present in the transaction by increment-

ing the frequency value of the respective item by

2. A branch is created for each transaction such that

nodes represent the items, level of nodes in a

branch is based on the sorted order and the count

of each node is set to 1. However, in construct-

ing the new branch for a transaction, the count of

each node along a common preﬁx is incremented

by 1, and nodes for the items following the pre-

ﬁx are created, linked accordingly and their values

are set to 1.

To facilitate tree traversal, an item header table

is built so that each item points to its occurrences

in the tree via a chain of node-links. From the item

frequencies, the respective support values are calcu-

lated. Using the lowest MIS value among all the items

(MIS), the tree-pruning process is performed on the

item header and MIS-tree to remove the items hav-

ing support less than the lowest MIS value among

all items. After tree-pruning, tree-merging process is

performed to generate the compact MIS-tree.

Table 1: Transaction dataset.

TID Items

1 bread, jam

2 bread, jam, ball

3 bread, jam, pen

4 bread, jam, pencils

5 bread, bat, ball

6 bed, pillow

7 bed, pillow

8 ball, bat

9 ball, bat

10 ball, bat

The compact MIS-tree is mined as follows. Each

item in L

is considered as a sufﬁx pattern, next its

conditional pattern base, which is a set of preﬁx-

paths in the MIS-tree is constructed and mining is per-

formed recursively on such a tree. The pattern growth

is achieved by the concatenation of the sufﬁx pattern

with the frequent patterns generated from the condi-

tional pattern.

For the dataset shown in Table 1, the extraction

of frequent patterns using CFP-growth algorithm is

illustrated using Example 1. For ease of explaining

this example we refer the support and MIS values of

the items in terms of support counts and MIS counts.

Example 1. For the transaction dataset shown in

Table 1, the itemset I = {bread, ball, jam, bat, pil-

low, bed, pencil, pen}. Let the MIS values (in

count) for bread, ball, jam, bat, pillow, bed, pen-

cil and pen be 4, 4, 3, 3, 2, 2, 2 and 2 respec-

tively. Now, using the MIS values for the items,

the CFP-growth approach sorts the items in de-

scending order of their MIS values and assigns the

frequency value of zero to every item. Thus, L

contain {{bread:0}, {ball:0}, {jam:0}, {bat:0},

{pillow:0}, {bed:0}, {pencil:0}, {pen:0}}. In the

ﬁrst scan of the dataset shown in Table 1, the ﬁrst

transaction “1: bread, jam” containing two items

is scanned in L

order i.e., {bread, jam} and the

frequencies of items “bread” and “jam” are up-

dated by 1 in L

. Next, a ﬁrst branch of tree is con-

structed with two nodes, hbread: 1i and hjam: 1i,

where “bread” is linked as a child of the root and

“jam” is linked as a child of “bread”. The second

transaction “2: bread, jam, ball” containing three

items “bread, ball, jam” in L

order and the fre-

quencies of the items are updated by incrementing

by 1. Next, the items in second transaction, or-

dered in L

, will result in a branch where “bread”

is linked to root, “ball” is linked to “bread” and

“jam” is linked to “ball”. However, this branch

shares the common preﬁx, “bread”, with the ex-

isting path for ﬁrst transaction. Therefore, the

AN IMPROVED FREQUENT PATTERN-GROWTH APPROACH TO DISCOVER RARE ASSOCIATION RULES

count of “bread” node is incremented by 1 and

new nodes are created for items “ball and jam”

such that “ball” is linked to “bread” and “jam” is

linked to “ball” and their node values are set to

1. The process is repeated until all the transac-

tions are completed. A node link table is built for

traversal. The constructed MIS-tree is shown in

Figure 1. Next, CFP-growth identiﬁes the lowest

MIS value among all the items i.e., 2 and try to

remove the items whose support value is less than

2. From the node table, ﬁrst, item “pencil” is re-

moved. Next, tree pruning is preformed on MIS-

tree to remove all the nodes pertaining to item

“pencil”. Next, the item “pen” is removed from

the node-link table and MIS-tree. After that, tree-

merging is performed to merge the branches. The

ﬁnal and compact MIS-tree is shown in Figure 1

with bold letter and think lines.

Mining the constructed MIS-tree is shown in Ta-

ble 2 and is summarized as follows. Start from

the last item in the item header table i.e., “bed”,

as the sufﬁx item. Then construct its conditional

pattern base for this sufﬁx item is as follows. In

the MIS-tree shown in Figure 1, “bed” occurs in

one node. The path formed from this node is

hpillow, bed: 2i. Therefore, considering “bed” as

sufﬁx, its corresponding preﬁx paths are hpillow:

2i, which form its conditional pattern base. Its

conditional MIS-tree contains only a single path,

hpillow: 2i. The single path generates all the

combinations of frequent patterns {pillow, bed:

2}. Next, by considering every item one after

another in the ascending order of their MIS val-

ues, the corresponding conditional pattern bases

and conditional MIS-tree are constructed to gen-

erate all frequent patterns are generated. The ﬁ-

nally generated frequent patterns are {{ bread},

{ball}, {jam}, {bat}, {pillow}, {bed}, {bread,

jam}, {bat, ball}, {pillow, bed}}.

The performance problem in the CFP-growth

approach is as follows. The CFP-growth constructs

compact MIS-tree involving the items having support

greater than the lowest MIS value among all the items.

The intuition behind this selection process is that no

frequent pattern will have support less than the lowest

MIS value among all the items. However, by consid-

ering the lowest MIS value among all items this ap-

proach considers certain infrequent items which will

never generate any frequent patterns. This results in

increased memory and runtime requirements. We il-

lustrate this scenario in Example 2.

Example 2. Let the set of items {U, V, W, X,

Y, Z} have support values {10%, 8%, 6%, 4%,

2%, 1%} respectively. Let the respective MIS val-

Item NL

Bread

Ball

Jam

&Bat

Pillow

Bed

MIS

Pen 1 2

Pencil 1 2

null{}

= |

Figure 1: MIS-tree. The compact MIS-tree is represented

with bold letters (ﬁrst six rows in the table) and the corre-

sponding think lines and circles in the tree.

ues be {9%, 9%, 7%, 4%, 3%, 2%}. Since the

lowest MIS value is 2%, any frequent pattern will

have support not less than 2%. Therefore, CFP-

growth considers set of items {U, V, W, X, Y} for

generating frequent patterns. The CFP-growth do

not consider item Z for generating frequent pat-

terns because its support (1%) is less than lowest

MIS value among all items (2%). However, it can

be observed that the infrequent item Y will never

generate any frequent pattern. The reason is that

any pattern involving item Y can have support at

most equivalent to 2%, which is less than the MIS

value of Y i.e., 3%.

3 PROPOSED APPROACH

In this section, we ﬁrst present the basic idea of the

proposed approach. Next, the algorithm is discussed.

Subsequently, we discuss how the proposed approach

is different from CFP-growth approach.

3.1 Basic Idea

In the proposed approach, we exploit the following

notions: “least minimum support” and “infrequent

leaf node pruning”.

Least Minimum Support. The frequent patterns

mined using multiple minsup values follow “sorted

closure property”. According to “sorted closure prop-

erty”, all the supersets involving the item having low-

est MIS value should be frequent in a frequent pattern.

So in every frequent pattern, frequent item represents

the item having the lowest MIS value. Therefore, it

can be argued that every frequent pattern will have

support greater than or equal to lowest MIS value

among all the frequent items. Thus, if we remove

KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval

Table 2: Mining the MIS-tree by creating conditional pattern bases in CFP-growth.

Item MIS Conditional Conditional Frequent patterns

pattern base MIS-tree generated

bed 2 {{pillow: 2}} hpillow: 2i {pillow, bed: 2}

pillow 2

bat 3 {{bread, ball: 1}, hball:4i {ball, bat: 4}

{ball:3}}

jam 3 {{bread,ball: 1}, hbread:4i {bread, jam: 4}

{bread: 3}}

ball 4 {{bread: 2}} hbread:2i {bread, ball: 2}

all the items whose support is less than the lowest

MIS value of the frequent item, no frequent pattern

will be missed. This notion is called “least minimum

support” (LMS) and it refers to the lowest MIS value

among all the frequent items. The signiﬁcance of this

notion is illustrated in Example 3.

Example 3. Continuing with the Example 2, it

can be observed that the set of items {U, X} are

frequent items. The lowest MIS value among

these items is 4%. Therefore, using LMS value

as 4%, the proposed approach prunes the set of

items {Y, Z} and considers {U, V, W, X} for fre-

quent pattern mining.

Let I be the set of all items in the transaction

dataset. Let C be the set of items considered by

CFP-growth approach for mining frequent patterns.

Let F be the set of items considered by ICFP-growth

approach for mining frequent patterns. Then, the

relation between I, C and F is as follows: F ⊆ C ⊆ I.

Infrequent Leaf Node Pruning: In the process of

mining compact MIS-tree using conditional pattern

bases, the sufﬁx item (or pattern) represents the item

having lowest MIS value. So if a sufﬁx item is an

infrequent item, based on “sorted closure property”,

it can be said that all the preﬁx paths of the respec-

tive sufﬁx item will also be infrequent. Therefore, the

ICFP-growth approach skips the construction of con-

ditional pattern bases for the infrequent sufﬁx items.

In the compact MIS-tree, the leaf nodes belong to in-

frequent items have no signiﬁcance because its preﬁx

paths (conditional pattern bases) are not used. The re-

sultant MIS-tree will still preserve the transaction de-

tails pertaining to frequent patterns even if we prune

the leaf nodes belonging to infrequent items. There-

fore, we propose that “infrequent leaf node pruning”

is performed such that every branch ends with the

node of a frequent item. We illustrate the “infrequent

leaf node pruning” in Example 4.

Example 4. Continuing with the Example 2 and

Example 3, let the MIS-tree derived after per-

forming a single scan on the dataset contain three

branches, say hU, Vi, hV, Wi and hW, Xi. Among

the set of items {U, V, W, X}, we know that

items V and W are infrequent items. First, let

us consider the item W, having relatively lowest

MIS value for pruning. In the MIS-tree gener-

ated, the branch hU, Vi do not contain any item

W and hence no pruning is performed. In the sec-

ond branch hV, Wi, there exists leaf node with

item W. Therefore, pruning is performed to gen-

erate a new branch hVi. In the third branch hW,

Xi, though there exists node of the item W, it is

not the leaf node. So no pruning is performed.

Thus the resulted MIS-tree contains hU, Vi, hVi

and hW, Xi. Next, select another infrequent item

i.e., V for pruning. In the newly generated MIS-

tree, the branch hU, Vi contains the leaf node V.

So pruning is performed to create a new branch

hUi. In the second branch hVi, the node V is a

leaf node. So the node is pruned from compact

MIS-tree. Since no node exists in the branch the

branch is deleted. In the third branch, hWi, exists

no node with the item V. So no pruning is per-

formed. Thus the ﬁnal resulted MIS-tree contains

only two branches hUi and hW, Xi.

3.2 The Algorithm

The ICFP-growth pre-assumes that for every item,

user speciﬁes the MIS values priori to its execution.

Therefore, using the priori information i.e., MIS val-

ues of the items, the frequent patterns are generated

with a single scan on the dataset. The proposed algo-

rithm generalizes the CFP-growth algorithm for ﬁnd-

ing frequent patterns. This approach involves three

steps. They are constructing the MIS-tree, extracting

compact MIS-tree and mining the compact MIS-tree

to mine frequent patterns. We now discuss each of

these steps in detail.

3.2.1 Constructing MIS-tree

The construction of MIS-tree in ICFP-growth algo-

rithm is shown in Algorithm 1 and described as fol-

AN IMPROVED FREQUENT PATTERN-GROWTH APPROACH TO DISCOVER RARE ASSOCIATION RULES

lows. The ICFP-growth algorithm accepts transaction

dataset (Trans), Itemset (I) and minimum item support

values (MIS) of the items as input parameters. Using

the input parameters, the ICFP-growth creates an ini-

tial MIS-tree which is similar to MIS-tree created by

CFP-growth (Lines 1 to 7 in Algorithm 1). (Refer to

Section 2 for knowing the construction of initial MIS-

tree using CFP-growth approach.)

3.2.2 Extracting Compact MIS-tree

Next, starting from the last item in the item-header ta-

ble (i.e., item having lowest MIS value) perform tree-

pruning operating by calling MisPruning procedure

(See, procedure 3) to remove the infrequent items

from the item-header table and MIS-tree. After one

item is pruned, move to immediate next item in item-

header table and perform tree-pruning. However, stop

tree-pruning process when the frequent item is en-

countered. The MIS value of this frequent item rep-

resents the LMS value. Let the resultant item header

table be MinFrequentItemHeaderTable. The items in

this header table may contain both frequent and in-

frequent items having support greater than the low-

est MIS value among all frequent items. The items

in the header table are referred as “quasi-frequent

items”. Call MisMerge procedure (See, procedure

4) to merge the tree. Finally, call InfrequentLeafN-

odePruning procedure (See, procedure 5) to prune the

infrequent leaf nodes in the MIS-tree. The resultant

MIS-tree is the compact MIS-tree.

3.2.3 Mining Frequent Patterns from Compact

MIS-tree

Mining the frequent patterns from the compact MIS-

tree is shown in Algorithm 6. The process of min-

ing the compact MIS-tree in ICFP-growth is almost

same as mining the compact MIS-tree in CFP-growth.

However, the variant between the two approaches is

that before generating conditional pattern base and

conditional MIS-tree for every item in the header of

the Tree, the ICFP-growth approach veriﬁes whether

the sufﬁx item in the header of the Tree is a frequent

item (Line 2 in Algorithm 6). If an sufﬁx item is not

a frequent item (or pattern) then the construction of

conditional pattern base and conditional MIS-tree are

skipped. The reason is as follows. In every frequent

pattern, the item having lowest MIS value should be

a frequent item (sorted closure property). In con-

structing the conditional pattern base for a sufﬁx item,

the sufﬁx item represents the item having lowest MIS

value. Therefore, if the sufﬁx item is an infrequent

item then all its preﬁx-paths (the patterns in which it

Algorithm 1. MIS-tree (Tran:transaction dataset, I:

itemset containing n items, MIS: minimum item sup-

port values for n items).

1: Let L represent the set of items sorted in nonde-

creasing order of their MIS values.

2: create the root of a MIS-tree, T, and label it as

“null”.

3: for each transaction t ∈ Tran do

4: sort all the items in t in L order.

5: count the support values of any item i, denoted

as S(i) in t.

6: Let the sorted items in t be [p|P], where p is the

ﬁrst element and P is the remaining list. Call

InsertTree([p|P], T).

7: end for

8: for j=n-1; j ≥ 0; –j do

9: if S[i

] < MIS[i

] then

10: Delete the item i

in header table.

11: call MisPruning(Tree, L[i

]).

12: else

13: break; //come out of pruning step.

14: end if

15: end for

16: Name the resulting table as MinFrequentItem-

HeaderTable.

17: Call MisMerge(Tree).

18: Call InfrequentLeafNodePruning(Tree).

Procedure 2. InsertTree ([p|P, T).

1: while P is nonempty do

2: if T has a child N such that p.item-

name=N.item-name then

3: N.count++.

4: else

5: create a new node N, and let its count be 1.

6: let its parent link be linked to T.

7: let its node-link be linked to the nodes with

the same item-name via the node-link struc-

ture;

8: end if

9: end while

Procedure 3. MisPruning (Tree, i

1: for each node in the node-link of i

in Tree do

2: if the node is a leaf then

3: remove the node directly;

4: else

5: remove the node and then its parent node

will be linked to its child node(s);

6: end if

7: end for

KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval

Procedure 4. MisMerge (Tree).

1: for each item i

in the MinFrequentItemHead-

erTable do

2: if there are child nodes with the same item-

name then then

3: merge these nodes and set the count as the

summation of these nodes’ counts.

4: end if

5: end for

Procedure 5. InfrequentLeafNodePruning(Tree).

1: choose the last but one item i

in MinFrequen-

tItemHeaderTable. That is, item having second

lowest MIS value.

2: repeat

3: if i

item is infrequent item then

4: using node-links parse the branches of the

Tree.

5: repeat

6: if i

node is the leaf of a branch then

7: drop the node-link connecting through

the child branch.

8: create a new node-link from the node

in the previous branch to node in the

coming branch.

9: drop the leaf node in the branch.

10: end if

11: until all the branches in the tree are parsed

12: end if

13: choose item i

which is next in the order.

14: until all items in MinFrequentItemHeaderTable

are completed

represents the item having lowest MIS value) will also

be infrequent.

After mining frequent patterns, the method give

in (Agrawal and Srikanth, 1994) can be used to ﬁnd

association rules.

4 EXPERIMENTAL RESULTS

4.1 Experimental Details

In this section, we present the performance compari-

son of CFP-growth and ICFP-growth approaches. We

are not comparing the ICFP-growth with MSApri-

ori and IMSApriori approaches. The reason being

that, CFP-growth is relatively efﬁcient than MSApri-

ori approach (Ya-Han Hu, 2004). The IMSApriori ap-

proach uses “iterative level-wise search” to discover

Algorithm 6. ICFP-growth (Tree: MIS-tree, L: set

of quasi-frequent items, MIS: minimum item support

values for the items in L).

1: for each item i

in the header of the Tree do

2: if i

is a frequent item then

3: generate pattern β = i

∪ α with support =

.support;

4: construct β’s conditional pattern base and

β’s conditional MIS-tree Tree β.

5: if Tree β 6=

0 then

6: call CpGrowth(Tree β, β, MIS(i

7: end if

8: end if

9: end for

Procedure 7. CpGrowth(Tree, α, MIS(α)).

1: for each i

in the header of Tree do

2: generate pattern β = i

∪ α with support =

.support.

3: construct β’s conditional pattern base and then

β’s conditional MIS-tree Tree

4: if Tree

0 then

5: call CpGrowth(Tree

, β, MIS(α)).

6: end if

7: end for

frequent patterns. So, the CFP-growth is relatively ef-

ﬁcient than IMSApriori approach.

We have evaluated the performance of proposed

approach by considering two kinds of datasets: syn-

thetic and real world datasets. The synthetic dataset

T10.I4.D100K, is generated with the data generator

(Agrawal and Srikanth, 1994), which is widely used

for evaluating association rule mining algorithms. It

contains 1,00,000 number of transactions, 886 items,

maximum number of items in a transaction is 29 and

the average number of items in a transaction is 12.

Another dataset is a real world dataset referred as re-

tail dataset. It contains 88,162 number of transac-

tions, 16,470 items, maximum number of items in a

transaction is 76 and the average number of items in

each transaction is 5.8.

4.2 Experiment 1

In this experiment, we present the results pertaining to

construction of compact MIS-tree by only exploiting

the “least minimum support” notion and not consider-

ing the “infrequent leaf node pruning” notion. In the

next subsection, we discuss the results by exploiting

both notions.

For this experiment, we need a method to assign

AN IMPROVED FREQUENT PATTERN-GROWTH APPROACH TO DISCOVER RARE ASSOCIATION RULES

400

500

600

700

800

900

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

LMS

ICFP-growth

CFP-growth

2(a)

Items participated

1500

1600

1700

1800

1900

2000

2100

2200

2300

0.1 0.105 0.11 0.115 0.12 0.125 0.13 0.135 0.14

LMS

ICFP-growth

CFP-growth

2(b)

Items participated

Figure 2: Number of items participated at different LMS values in (a) Synthetic and (b) Retail datasets.

9000

10000

11000

12000

13000

14000

15000

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

Compact MIS-tree size (KB)

LMS

ICFP-growth

CFP-growth

3(a)

0.14

Compact MIS-tree size (KB)

6500

7000

7500

8000

8500

9000

9500

10000

0.1 0.105 0.11 0.115 0.12 0.125 0.13 0.135

LMS

ICFP-growth

CFP-growth

3(b)

Figure 3: The size of the compact MIS-tree at different LMS values in (a) Synthetic and (b) Retail datasets.

MIS values to items in the dataset. We use the sup-

ports of the items in the dataset as the basis for as-

signing MIS values. Specially, we use the following

formulas:

MIS(i

) =











M(i

) if M(i

) > LMS

LMS else if M(i

) < LMS

and S(i

) > LMS

LMIS else











(2)

M(i

) = S(i

) − SD

where, SD is a user-speciﬁed support difference

value varied between 0% to 1%, S(i

) refers to sup-

port of an item equal to f(i

)/N, (f(i

) represents fre-

quency of i

and N is the number of transactions

in a transaction dataset), LMS corresponds to user-

speciﬁed lowest minimum support value, which rep-

resents lowest MIS value of a frequent item and

LMIS corresponds to user-speciﬁed least minimum

item support value, which represents the lowest MIS

value among all items in the transaction dataset. The

LMS value will be always be greater than or equal to

LMIS value.

For both T10.I4.D100k and Retail datasets, the

SD and LMIS values are set at 0.1% and 0.1% re-

spectively. By varying the LMS values, the com-

pact MIS-tree is constructed using the proposed ap-

proach. It can be observed that in the CFP-growth

approach there is no scope to vary LMS values. (In

order to make the chosen MIS value to represent the

LMS value, the items which are having support values

less than the LMS value are converted into infrequent

items.)

Both Figure 2(a) and Figure 2(b) show the number

of items participated in generating frequent patterns at

different LMS values in both T10.I4.D100k and Re-

tail datasets. It can be observed that as the LMS value

increases the number of items which haveparticipated

in generating the frequent patterns also got reduced in

ICFP-growth approach. However, in CFP-growth the

number of items participating in generating frequent

patterns remains the same.

Both Figure 3(a) and Figure 3(b) provide the in-

formation regarding the size of compact MIS-tree

generated at different LMS values in both datasets. It

can be observed that as the LMS value increases the

size of the compact MIS-tree gets reduced in ICFP-

growth approach. The reason being that the num-

ber of items participating in generating frequent pat-

terns also get reduced. However, the size of the com-

pact MIS-tree generated by CFP-growth do not get

KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval

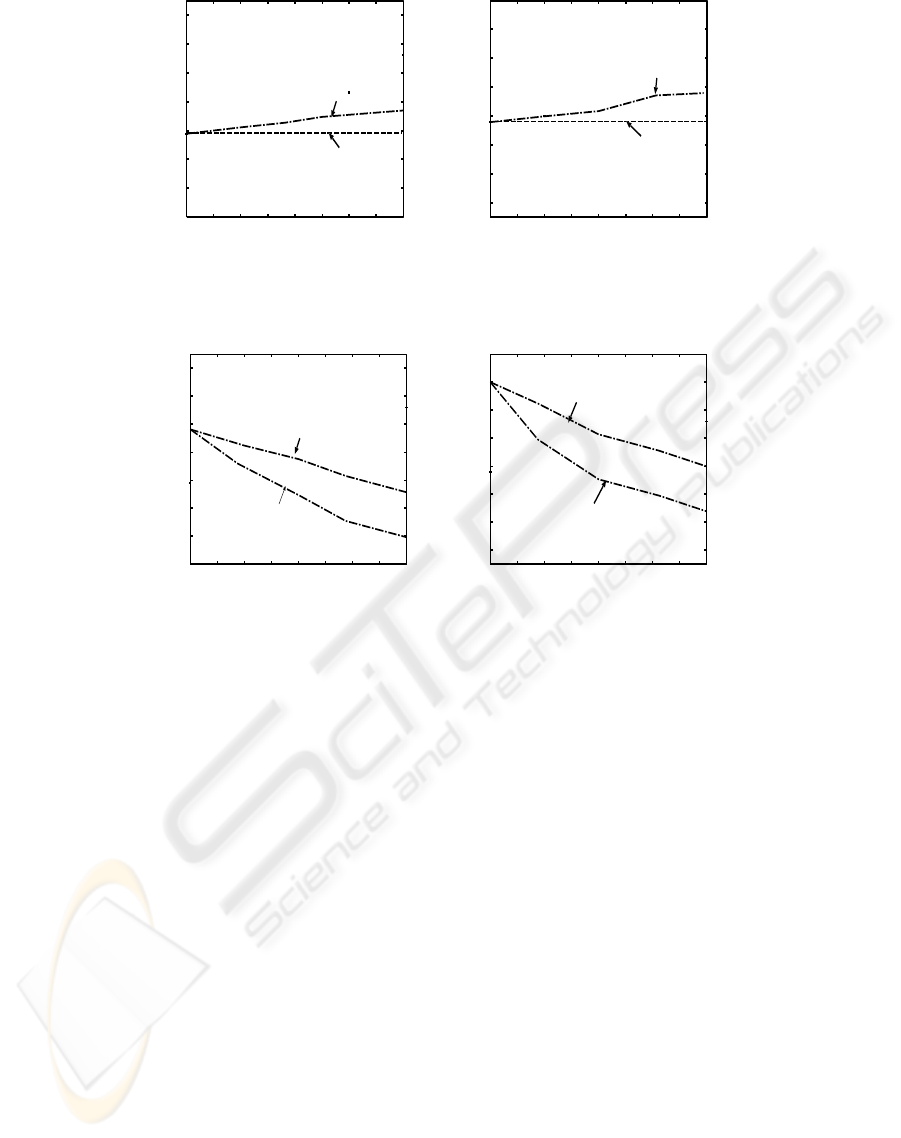
4(a)

100

110

120

130

140

150

160

170

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

runtime (sec)

LMS

ICFP-growth

CFP-growth

100

110

120

130

140

150

0.1 0.105 0.11 0.115 0.12 0.125 0.13 0.135 0.14

runtime (sec)

ICFP-growth

CFP-growth

4(b)

LMS

Figure 4: Runtime for generating compact MIS-tree at different LMS values in (a) Synthetic and (b) Retail datasets.

5(a)

300

310

320

330

340

350

360

370

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

runtime (sec)

LMS

ICFP-growth

CFP-growth

230

240

250

260

270

280

290

300

0.1 0.105 0.11 0.115 0.12 0.125 0.13 0.135 0.14

runtime (sec)

ICFP-growth

CFP-growth

5(b)

LMS

Figure 5: Runtime for generating compact MIS-tree and frequent patterns at different LMS values in (a) Synthetic and (b)

Retail datasets.

reduced. The reason is that CFP-growth fails to prune

the items which will not generate any frequent pat-

terns.

Both Figure 4(a) and Figure 4(b) provide the in-

formation regarding the “runtime” taken to generate

compact MIS-tree at different LMS values in both

datasets. It can be observed that the ICFP-growth re-

quires relatively more runtime than CFP-growth ap-

proach. The reason is ICFP-growth approach has

to prune relatively more number of items from the

header table and MIS-tree as compared with CFP-

growth.

Both Figure 5(a) and Figure 5(b) provide the in-

formation regarding the “runtime” taken to construct

compact MIS-tree and generate frequent patterns at

different LMS values in both datasets. In this exper-

iment the ICFP-growth takes relatively less runtime

than CFP-growth approach. It can be noted that even

though ICFP-growth takes more time for constructing

compact MIS-tree over CFP-growth approach, over-

all it takes less time to extract frequent patterns. The

reason is the ICFP-growth approach skips construc-

tion of conditional pattern bases for the sufﬁx items

(or patterns) which are infrequent.

4.3 Experiment 2

In this experiment, we present the results by exploit-

ing both “least minimum support” and “infrequent

leaf node pruning” notions.

The experiment is conducted as follows. In this

experiment, the MIS value for the each item is ﬁxed

equal to a random number between 0.1% to 1% of

the number of transactions in the dataset. We ran-

domly select some percentage of items which vary

from 0% to 20% and made them infrequent by setting

MIS values greater than their support values. By ﬁx-

ing LMS values at 0.1% and 0.25%, we compute the

size of compact MIS-tree by varying percentage of in-

frequent items under both the approaches. The corre-

sponding results are shown in Figure 6(a) and Figure

6(b) for the datasets T10.I4.D100kand Retail datasets

respectively. The results show that the size of the

compact MIS-tree remains the same at different per-

centage values of infrequent items under CFP-growth

approach, whereas the size of the compact MIS-tree

reduces signiﬁcantly at different percentage values of

infrequent items under ICFP-growth approach. The

reason is the ICFP-growth approach pruned the leaf

AN IMPROVED FREQUENT PATTERN-GROWTH APPROACH TO DISCOVER RARE ASSOCIATION RULES

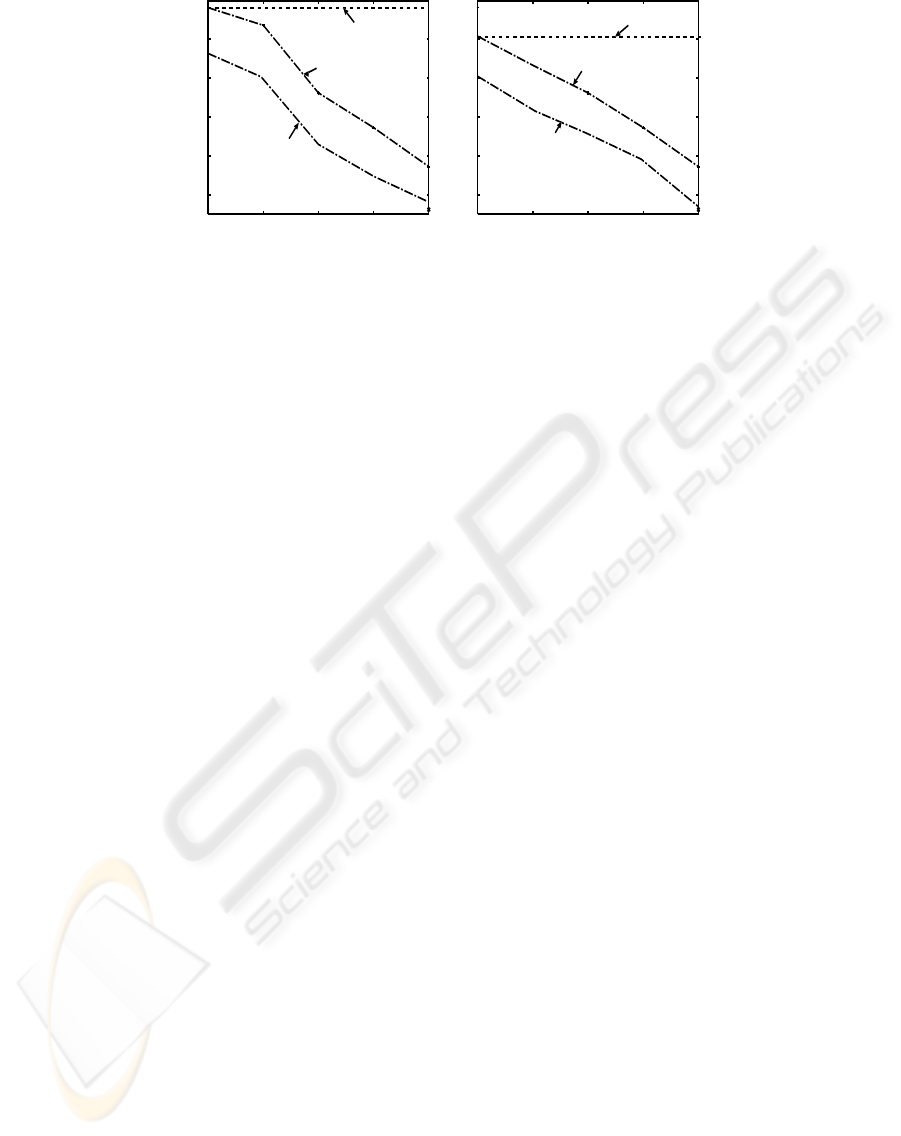
6000

8000

10000

12000

14000

16000

0 5 10 15 20

Compact MIS-tree size (KB)

% of infrequent items

CFP-growth

ICFP-growth

(LMS=0.1)

ICFP-growth

(LMS=0.25)

7500

8000

8500

9000

9500

10000

0 5 10 15 20

Compact MIS-tree size (KB)

% of infrequent items

CFP-growth

ICFP-growth

(LMS=0.1)

ICFP-growth

(LMS=0.25)

6(a) 6(b)

Figure 6: Compact MIS-tree sizes at different percentage of infrequent items in (a) Synthetic and (b) Retail datasets.

nodes belonging to infrequent items.

5 CONCLUSIONS AND FUTURE

WORK

To extract rare association rules, efforts are being

made in the literature by extending the “multiple min-

imum support” framework to FP-growth approach. In

this paper, we have proposed an improved FP-growth

approach with “multiple minimum support” frame-

work by exploiting the notions such as “least min-

imum support” and “infrequent leaf node pruning”.

The proposed approach reduces the memory for con-

structing conditional frequent pattern tree and runtime

for generating frequent patterns. The experimental re-

sults on both synthetic and real world datasets show

that the proposed approach improves the performance

over the existing approaches.

As a part of future work, we are going to inves-

tigate appropriate methodology for assigning conﬁ-

dence values in a dynamic manner to generate rare

association rules. We are also going to investigate

appropriate methodology for automatic calculation of

MIS values for the items.

ACKNOWLEDGEMENTS

The work has been carried out with the support from

Nokia Global University Grant.

REFERENCES

Agrawal, R. and Srikanth, R. (1994). Fast algorithms for

mining association rules. In International Conference

on Very Large Databases.

B. Liu, W. H. and Ma, Y. (1999). Mining association rules

with multiple minimum supports. In ACM Special In-

terest Group on Knowledge Discovery and Data Min-

ing Explorations.

G. Melli, R. Z. O. and Kitts, B. (2006). Introduction to

the special issues on successful real-world data min-

ing applications. In ACM Special Interest Group on

Knowledge Discovery and Data Mining Explorations,

volume 8, Issue 1.

H. Jiawei, P. Jian, Y. Y. and Runying, M. (2004). Min-

ing frequent patterns without candidate generation: A

frequent-pattern tree approach. In ACM SIGMOD

Workshop on Research Issues in Data Mining and

Knowledge Discovery.

J. Hipp, U. G. and Nakhaeizadeh, G. (2000). Algorithms for

association rule mining a general survey and compar-

ision. In ACM Special Interest Group on Knowledge

Discovery and Data Mining, Volume 2, Issue 1.

Kiran, R. U. and Reddy, P. K. (2009). An improved multiple

minimum support based approach to mine rare asso-

ciation rules. In IEEE Symposium on Computational

Intelligence and Data Mining.

Mannila, H. (1997). Methods and problems in data mining.

In International Conference on Database Theory.

R. Agrawal, T. I. and Swami, A. (1993). Mining association

rules between sets of items in large databases. In ACM

Special Interest Group on Management Of Data.

Weiss, G. M. (2004). Mining with rarity: A unifying frame-

work. In ACM Special Interest Group on Knowledge

Discovery and Data Mining Explorations.

Weiss, S. and Kulikowski, C. A. (1991). Computer systems

that learn: Classiﬁcation and prediction models from

statistics. In Neural Nets, Machine Learning, and Ex-

pert Systems. Morgan Kaufmann.

Xu, R. (2005). Survey of clustering algorithms. In IEEE

Transactions on Neural Networks.

Ya-Han Hu, Y.-L. C. (2004). Mining association rules with

multiple minimum supports: A new algorithm and a

support tuning mechanism. In Decision Support Sys-

tems.

KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval