SELECTING CATEGORICAL FEATURES IN
MODEL-BASED CLUSTERING
Cl´audia M. V. Silvestre
Escola Superior de Comunicac¸˜ao Social, Lisboa, Portugal
Margarida M. G. Cardoso
ISCTE, Business School, Lisbon University Institute, Lisboa, Portugal
M´ario A. T. Figueiredo
Instituto de Telecomunicac¸ ˜oes, Instituto Superior T´ecnico, Lisboa, Portugal
Keywords:
Cluster analysis, Finite mixture models, Feature selection, EM algorithm, Categorical variables.
Abstract:
There has been relatively little research on feature/variable selection in unsupervised clustering. In fact, feature
selection for clustering is a challenging task due to the absence of class labels for guiding the search for
relevant features. The methods proposed for addressing this problem are mostly focused on numerical data.
In this work, we propose an approach to selecting categorical features in clustering. We assume that the data
comes from a finite mixture of multinomial distributions and implement a new expectation-maximization (EM)
algorithm that estimate the parameters of the model and selects the relevant variables. The results obtained on
synthetic data clearly illustrate the capability of the proposed approach to select the relevant features.
1 INTRODUCTION
Clustering techniques are commonly used in several
research and application areas, with the goal of dis-
covering patterns (groups) in the observed data. More
and more often, data sets have a large number of fea-
tures (variables), some of which may be irrelevant
for the clustering task and adversely affect its perfor-
mance. Deciding which subset of the complete set of
features is relevant is thus a fundamental task, which
is the goal of feature selection (FS). Other reasons
to perform FS include: dimensionality reduction, re-
moval of noisy features, providing insight into the un-
derlying data generation process. Whereas FS is a
classic and well studied topic in supervised learning
(i.e., in the presence of labelled data), the absence of
labels in clustering problems makes unsupervised FS
a much harder task, to which much less attention has
been paid. A recent review and evaluation of several
FS methods in clustering can be found in (Steinley
and Brusco, 2008).
Most work on FS for clustering has focused on
numerical data, namely on Gaussian-mixture-based
methods (Constantinopoulos et al., 2006), (Dy and
Brodley, 2004), (Law et al., 2004); work on FS for
clustering categorical data is much rarer. In this work,
we propose an embedded approach (as opposed to a
wrapper or a filter (Dy and Brodley, 2004)) to FS in
categorical data clustering. We work in the common
frameworkfor categorical data clustering in which the
data is assumed to originate from a multinomial mix-
ture. We assume that the number of mixture com-
ponents is known and use an EM algorithm, together
with an MML (minimum message length) criterion to
estimate the mixture parameters (Figueiredo and Jain,
2002), (Law et al., 2004). The noveltyof the approach
is that it avoids combinatorial search: instead of se-
lecting a subset of features, the probabilities that each
feature is relevant are estimated. This work extends
that of (Law et al., 2004), (which was restricted to
Gaussian mixtures) to deal with categorical variables.
The paper is organized as follows. Section 2 re-
views the EM algorithm, introduces the notion of
feature saliency, and describes the proposed method.
Section 3 reports experimental results. Section 4 con-
cludes the paper and discusses future research.
303
M. V. Silvestre C., M. G. Cardoso M. and A. T. Figueiredo M. (2009).
SELECTING CATEGORICAL FEATURES IN MODEL-BASED CLUSTERING.
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval, pages 303-306
DOI: 10.5220/0002303203030306
Copyright
c
 SciTePress

2 SELECTING CATEGORICAL
FEATURES
Law, Figueiredo and Jain (Law et al., 2004) devel-
oped a new EM variant to estimate the probability that
each feature is relevant, in the context of (Gaussian)
mixture-based clustering. That algorithm estimates a
Gaussian mixture model, based on the MML criterion
(Wallace and Boulton, 1968). Their approach seam-
lessly merges estimation, model, and feature selec-
tion in a single algorithm. Our work is based on that
approach and implements a new version for cluster-
ing categorical data via the estimation of a mixture of
multinomials.
Let y =
n
y
1
,...,y
n
o
be a sample of n indepen-
dent and identically distributed random variables,
Y = {Y
1
,...,Y
n
} with Y
i
= {Y
i1
,...,Y
iL
} is a L-
dimensional random variable. It is said that Y follows
a K component finite mixture distribution if its log-
likelihood can be written as
log
n
∏
i=1
f(y
i
|θ) =
n
∑
i=1
log
K
∑
k=1
α
k
f(y
i
|θ
k
)
where α
1
,...,α
K
are the mixing probabil-
ities (α
k
≥ 0,k = 1,..,K and
∑
K
k=1
α
k
= 1),
θ = (θ
1
,..,θ
K
,α
1
,..,α
K
) is the set of the param-
eters of the model, and θ
k
is the set of parameters
defining the k-th component. In our case, for
categorical data, f(.) is the probability function
of a multinomial distribution. Assuming that the
features are conditionally independent given the
component-label, the log-likelihood is
log
n
∏
i=1
f

y
i
|θ

=
n
∑
i=1
log
K
∑
k=1
α
k
L
∏
l=1
f(y
il
|θ
kl
).
2.1 EM Algorithm
The EM algorithm (Dempster et al., 1997) has been
often used as an effective method to obtain maximum
likelihood estimates based on incomplete data. As-
suming that observed variable Y
i
for i = 1,...,n (the
incomplete data) is augmented by a cluster-label vari-
able Z
i
which is a set of K binary indicator latent vari-
ables, the complete log-likelihood is
log
n
∏
i=1
f

y
i
,z
i
|θ

=
n
∑
i=1
K
∑
k=1
z
ik
log

α
k
f(y
i
|θ
k
)

Each iteration of the EM algorithm consists of two
steps
• E-step: calculates the expectation of the complete
log-likelihood, whit respect to the conditional dis-
tribution of Z given y under the current estimates
of the parameter
E
h
log f(y,Z|θ)|y,
ˆ
θ
(t)
i
= log f

y,E
h
Z|y,
ˆ
θ
(t)
i
|θ

,
where the equality results from the fact that the
complete log-likelihood is linear with respect to
the elements of Z.
• M-step: finds the parameters which mazimize
ˆ
θ
(t+1)
= argmax
θ

log f

y,E
h
Z|y,
ˆ
θ
(t)
i
|θ

2.2 The Saliency of Categorical
Features
There are different definitions of feature irrelevancy;
Law et al (Law et al., 2004) adopt the following one:
a feature is irrelevant if its distribution is independent
of the cluster labels, i.e., an irrelevant feature has a
density which common to all clusters. The probabil-
ity functions of relevantand irrelevant features are de-
noted by p(.) and q(.), respectively. For categorical
features, p(.) and q(.) refer to the multinomial distri-
bution. Let B = (B
1
,...B
L
) be the binary indicators of
the features, where B
l
= 1 if the feature l is relevant
and zero if irrelevant.
Defining feature saliency as the probability of
the feature being relevant, ρ
l
= P(B
l
= 1) the log-
likelihood is (the proof is in Law et al., 2004)
log
n
∏
i=t
f

y
i
|θ

=
n
∑
i=1
log
K
∑
k=1
α
k
L
∏
l=1
h
ρ
l
p

y
il
|θ
kl

+ (1− ρ
l
)q

y
l
|θ
l
i
The feature saliencies are estimated using an EM
variant based on the MML criterion which encourages
the saliencies of the relevant features to go to 1 and
the irrelevant features to go to zero, thus pruning the
feature set.
2.3 The Proposed Method
We adopt the approach proposed by Law et al (Law
et al., 2004) which is based on the MML criterion
(Figueiredo and Jain, 2002). This criterion chooses
the model providing the shortest description (in an in-
formation theory sense) of the observations (Wallace
and Boulton, 1968). Under the MML criterion, for
categorical features, the estimate of θ is the one that
minimizes the following description length function:
KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval
304

Initialization: set the parameters of the mixture components randomly and the common distribution to cover all the data
set the feature saliency of all features to 0.5
store the initial log-likelihood and the initial message length (mindl is initialized with this value)
continue ← 1
while continue do
while differences on likelihood are significant do
M-step
E-step
if ρ
l
= 1,q(y
l
|θ
l
) is pruned
if ρ
l
= 0,p(y
l
|θ
kl
) is pruned for all k
Compute the log-likelihood and the current message length (ml)
end while
if ml < mindl
mindl ← ml
update all the parameters of the model
end if
if there are saliencies /∈ {0,1}
prune the variable with the smallest saliency
else
continue ← 0
end if
end while
Figure 1: The algorithm.
l(y,θ) = − log f(y|θ) +
K + L
2
logn
+
L
∑
l=1, ρ
l
6=0
c
l
− 1
2
K
∑
k=1
log(nα
k
ρ
l
)
+
L
∑
l=1, ρ
l
6=1
c
l
− 1
2
log(n(1− ρ
l
))
where c
l
is the number of categories of feature l. Us-
ing a Dirichlet-type prior for the saliencies,
p(ρ
1
,...,ρ
L
) ∝
L
∏
l=1
ρ
−kc
l
2
l
(1− ρ
l
)
c
l
2
and from a parameter estimation point of view, l(y,θ)
is equivalent to a posterior density. Since Dirichlet-
type prior is conjugate with the multinomial, the EM
algorithm to maximize −l(y,θ) is
E-step: Compute the following quantities
P[Z
ik
= 1|Y
i
,θ]
=
α
k
∏
L
l=1
h
ρ
l
p

y
il
|θ
kl

+ (1− ρ
l
)q

y
l
|θ
l
i
∑
K
k=1
α
k
∏
L
l=1
h
ρ
l
p

y
il
|θ
kl

+ (1− ρ
l
)q

y
l
|θ
l
i
u
ikl
=
ρ
l
p

y
il
|θ
kl

ρ
l
p

y
il
|θ
kl

+ (1− ρ
l
)q

y
il
|θ
l

P[Z
ik
= 1|Y
i
,θ]
v
ikl
= P[Z
ik
= 1|Y
i
,θ] − u
ikl
M-step: Update the parameter estimates accord-
ing to
ˆ
α
k
=
∑
i
P[Z
ik
= 1|Y
i
,θ]
n
,
ˆ
θ
klc
=
∑
i
u
ikl
y
ilc
∑
c
∑
i
u
ikl
y
ilc
,
ˆ
ρ
l
=
∑
ik
u
ikl
−
K(c
l
−1)
2
!
+
∑
ik
u
ikl
−
K(c
l
−1)
2
!
+
+
∑
ik
v
ikl
−
c
l
−1
2
!
+
where (·)
+
is defined as (a)
+
= max{a,0}.
If, after convergence of EM, all the saliencies are
zero or one the algorithm stops. Otherwise, we check
if pruning the feature which has the smallest saliency
produces a better message length. This procedure
is repeated until all the features have their saliencies
equal to zero or one. At the end, we choose the model
with the minimum value of l(y,θ). The algorithm is
summarized in Fig. 1.
3 EXPERIMENTS
We use two types of synthetic data: in the first type,
the irrelevant features have exactly the same distri-
bution for all components. Since with real data, the
irrelevant features can have similar (but not exactly
equal) distributions within the mixture components,
we consider a second type of data where we simu-
late irrelevantfeatures with “similar” distributions be-
tween the components. In both cases, the irrelevant
SELECTING CATEGORICAL FEATURES IN MODEL-BASED CLUSTERING
305

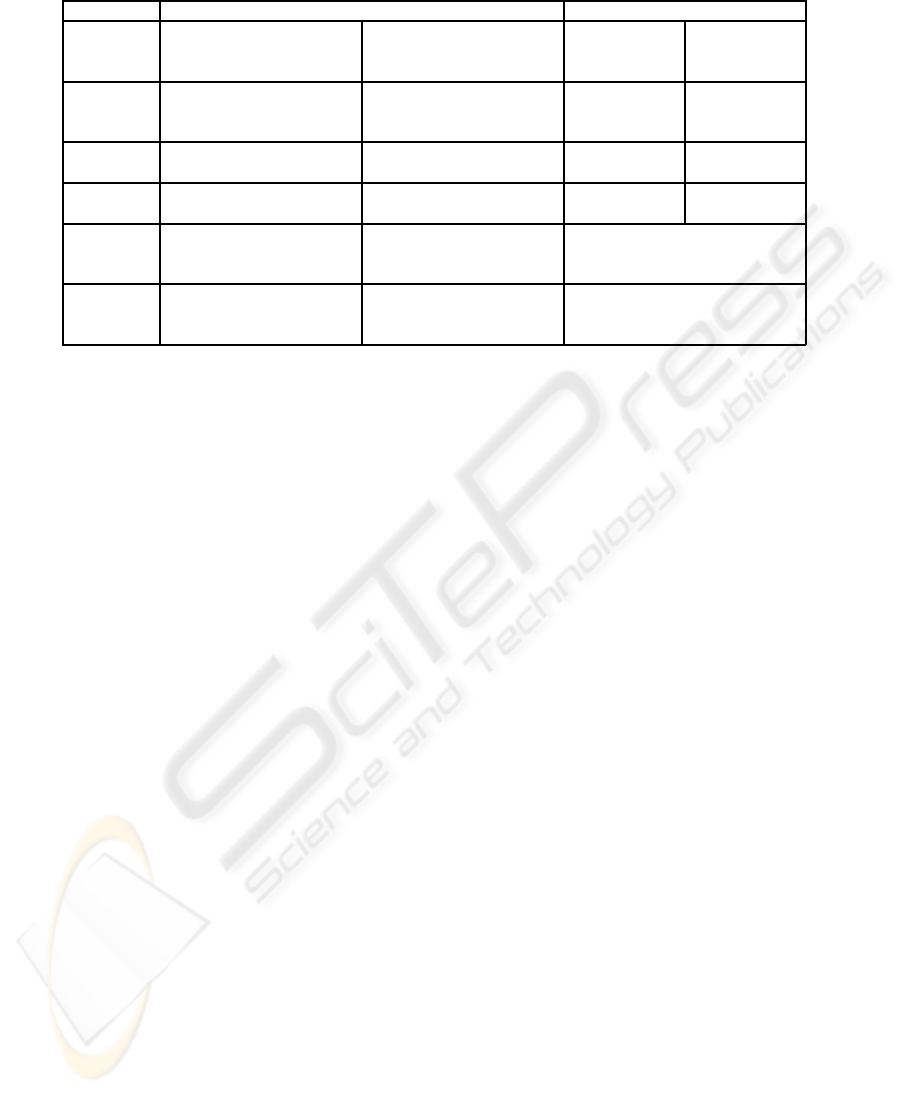
Table 1: Probabilities of the clustering five base variables categories.
Synthetic data Estimated parameters
Component 1 Component 2 Component 1 Component 2
Number of samples: 400 Number of samples: 500
α
1
= 0.4444 α
2
= 0.5556
b
α
1
= 0.4444
b
α
2
= 0.5556
Variable 1 0.7 0.1 0.6953 0.0988
0.2 0.3 0.2013 0.3024
0.1 0.6 0.1034 0.5988
Variable 2 0.2 0.7 0.2007 0.6936
0.8 0.3 0.7994 0.3064
Variable 3 0.4 0.6 0.4029 0.5996
0.6 0.4 0.5971 0.4004
Variable 4 0.5 0.49 0.4946
0.2 0.22 0.2049
0.3 0.29 0.3005
Variable 5 0.3 0.31 0.3119
0.3 0.30 0.2999
0.4 0.39 0.3882
features are also distributed according to a multino-
mial distribution. The numerical experiments refer
to 8 simulated data sets. According to the obtained
results using the proposed EM variant, the estimated
probabilities corresponding to the categorical features
almost exactly match the actual (simulated) probabil-
ities. In Table 1 we present results which refer to one
data set with 900 observations and 5 categorical vari-
ables (features). The first three variables are relevant
and the last two are irrelevant, with “similar” distribu-
tions between components. The variables 1, 4 and 5
have 3 categories each and the variables 2 and 3 have
2 categories.
4 CONCLUSIONS AND FUTURE
RESEARCH
In this work, we describe a feature selection method
for clustering categorical data. Our work is based on
the commonly used framework which assumes that
the data comes from a multinomial mixture model
(we assume that the number of components of the
mixture model is known). We adopt a specific defini-
tion of feature irrelevancy, based on the work of (Law
et al., 2004), which we believe is more adequate than
alternative formulations (Talavera, 2005) that tends to
discard features which are uncorrelated. We use a new
variant of the EM algorithm, together with an MML
(minimum message length) criterion, to estimate the
parameters of the mixture and select the relevant vari-
ables.
The reported results clearly illustrate the ability of
the proposed approach to recover the ground truth on
data concerning the features’ saliency. In future work,
we will implement the simultaneous selection of fea-
tures and the number of components, based on a sim-
ilar approach and illustrate the proposed approach us-
ing real data sets.
REFERENCES
Constantinopoulos, C., Titsias, M. K., and Likas, A. (2006).
Bayesian feature and model selection for gaussian
mixture models. IEEE Transactions on Pattern Anal-
ysis and Machine Intelligence, 28:1013–1018.
Dempster, A., Laird, N., and Rubin, D. (1997). Maxi-
mum likelihood estimation from incomplete data via
the em algorithm. Journal of Royal Statistical Society,
39B:1–38.
Dy, J. and Brodley, C. (2004). Feature selection for unsu-
pervised learning. Journal of Machine Learning Re-
search, 5:845–889.
Figueiredo, M. and Jain, A. (2002). Unsupervised learning
of finite mixture models. IEEE Transactions on Pat-
tern Analysis and Machine Intelligence, 24:381–396.
Law, M., Figueiredo, M., and Jain, A. (2004). Simultaneous
feature selection and clustering using mixture models.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 26:1154–1166.
Steinley, D. and Brusco, M. (2008). Selection of variables
in cluster analysis an empirical comparison of eight
procedures. Psychometrika, 73:125–144.
Talavera, L. (2005). An evaluation of filter and wrapper
methods for feature selection in categorical clustering.
Advances in Intelligent Data Analysis VI, 3646:440–
451.
Wallace, C. and Boulton, D. (1968). An information
measure for classification. The Computer Journal,
11:195–209.
KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval
306