MULTI-SEMANTIC APPROACH TOWARDS A GENERIC FORMAL

SOLVER OF TOOL PLACEMENT FOR PERCUTANEOUS SURGERY

Caroline Essert-Villard, Claire Baegert and Pascal Schreck

LSIIT - Universit

e de Strasbourg, Boulevard Sebastien Brant, 67412 Illkirch, France

Keywords:

Constraint solving, Surgery planning, Meta-programming.

Abstract:

In this paper, we study the multiple points of view when generalizing a method based on many criteria opti-

mization, in the framework of percutaneous surgery planning. The aim of the prototype is to ﬁnd an optimal

position of surgical tools to help the surgeons in planning the intervention. We explain how, with a formal

geometric solver and meta programming, we intend to build a modular tool, capable of being extended to new

interventions, with few programming efforts.

1 INTRODUCTION

Nowadays, an increasing number of cancers are

treated by using minimally invasive techniques, such

as percutaneous radiofrequency, cryoablation, or mi-

crowave. These treatments have many advantages,

but an important drawback is that the process gener-

ally involves a difﬁcult and tedious planning phase,

mainly relying on the study of the images of the pa-

tient (MRI, CT, ...), acquired before the intervention.

Sometimes, a secure planning can not be found, pro-

hibiting such an intervention.

In previous works, we presented a speciﬁc method

to assist the surgeon in planning percutaneous Ra-

dioFrequency Ablations (RFA) for liver tumors,

thanks to an automatic computation of an optimal

needle trajectory. We observed a lot of similarities

between the planning of this intervention and other

percutaneous procedures (cryoablation), or kinds of

surgery (e.g. Deep Brain Stimulation (DBS)).

This paper exposes how we analyzed similarities

that leaded us to a generalization of our method, us-

ing a geometric formalization of the data and a formal

geometric constraint solver. In the following section,

after a brief review of other related works in the ﬁelds

of surgery planning, we ﬁrst recall our previous re-

sults. Then, we expose our analysis of the framework

and explain our approach to extend the solver, and ex-

plain our choice of meta programming.

2 RELATED WORKS

In the domain of assistance to surgery planning,

among which percutaneous interventions, various

tools already exist. Most of them are simulators, mod-

elling what will be the effect of a treatment, for a

given placement of tools proposed by the surgeon.

However, this forces the surgeon to perform him-

self/herself the trial and error search. Other authors

proposed interesting attempts of automatic methods,

but they have important drawbacks. In (Altrogge

et al., 2006), authors do not take into account the pres-

ence of surrounding organs. Authors of (Lung et al.,

2004) and (Adhami and Coste-Mani

ere, 2003) con-

fess a long computation time, and the ﬁrst one algo-

rithm is only in 2D. In (Brunenberg et al., 2007), au-

thors restrict the research to a limited set of possible

entry points, avoiding possibly good trajectories to be

discovered. To our knowledge, very few automatic

methods exist, and they are all very speciﬁc to one

type of intervention. In this study, we focus on the

genericity of the solving process for a set of percuta-

neous interventions sharing a lot of similarities.

In previous papers (Baegert et al., 2007a; Baegert

et al., 2007b), we explained our method for provid-

ing automatically an optimal needle placement, in the

framework of percutaneous RFA preoperative plan-

ning. The rules governing these interventions are col-

lected from literature, observations, discussions with

experimented surgeons. They are implemented in the

program as functions, and solved using the patients

443

Essert-Villard C., Baegert C. and Schreck P. (2009).

MULTI-SEMANTIC APPROACH TOWARDS A GENERIC FORMAL SOLVER OF TOOL PLACEMENT FOR PERCUTANEOUS SURGERY.

In Proceedings of the International Conference on Knowledge Engineering and Ontology Development, pages 443-446

DOI: 10.5220/0002303804430446

 SciTePress

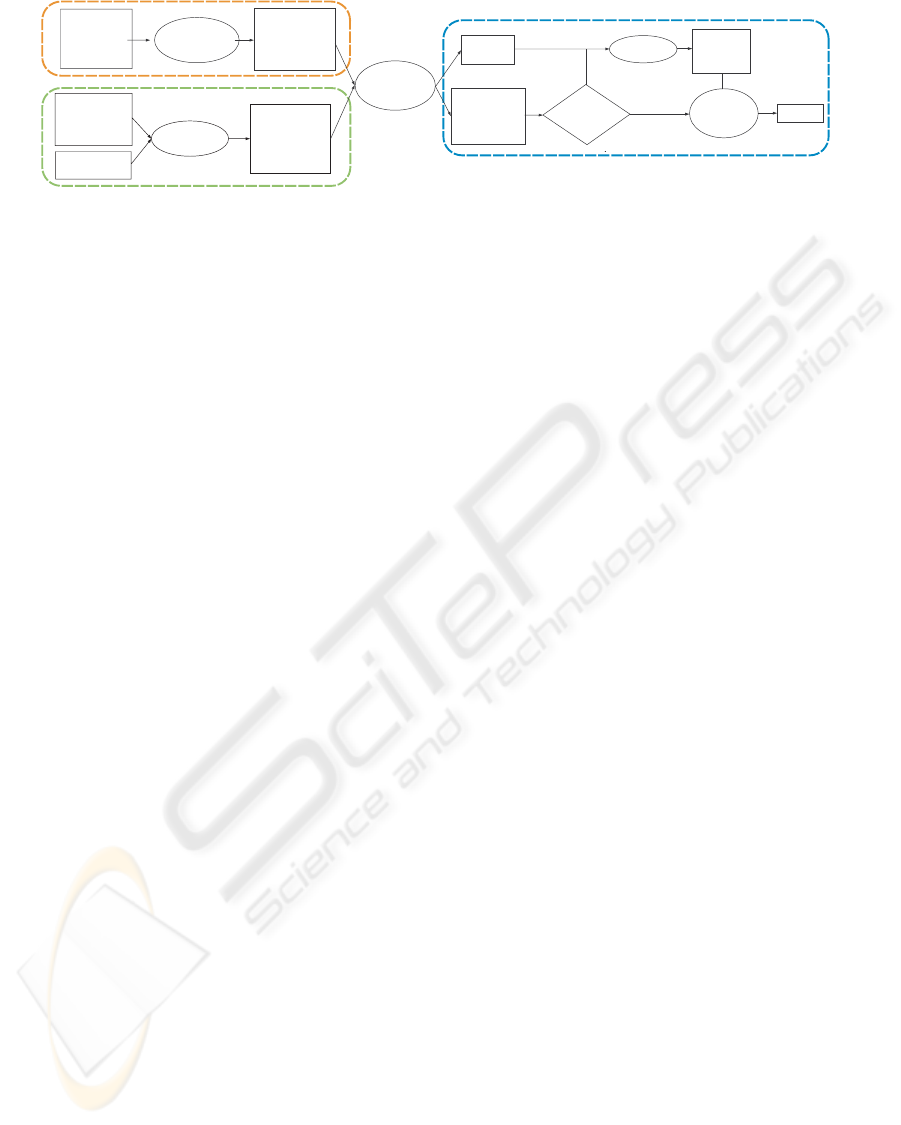
Intervention

Technique

(Literature,Surgeon's

Expertise,Case Studies)

Set of

Geometric and

Mathematic

Rules

(constraints)

Formalization

Devices

Specifications

Patient

Images

(MRI, CT, ...)

Patient Data

(3D

reconstructed

structures)

Reconstruction

Solution

Space

Optimal

Solution

(automatically

proposed)

Proposed

Solution

is OK

Navigation

Validation

Solution

Optimal

Solution

(manual)

yes

Solution

Geometric

Constraint

Solving

Patients data

Interventions data

Solution treatment

Figure 1: Process diagram.

images as input data. “Avoiding vital structures”, and

“minimizing the damages on healthy cells” are exam-

ples of rules that are translated into “eliminating solu-

tions crossing any organ mesh”, and “choosing those

minimizing the volume of the effect of the treatment”.

The output is a solution space constituted by the set

of possible solutions, and an optimal solution among

them. In Fig.1, a diagram showing the overall work-

ﬂow is shown. The data speciﬁc to a type of interven-

tion is deﬁned once for all for a type of intervention,

and is currently included in the code of the solver.

3 PERCUTANEOUS

INTERVENTIONS

3.1 Motivation

Our previous method and the associated software

were designed for a speciﬁc kind of intervention. The

only modiﬁable parameters were the weighting coef-

ﬁcients applied to the different constraints. We aim

at generalizing our approach, in order to be able to

easily take into account: new constraints, new kinds

of interventions, according to the different points of

views of the actors of the process.

3.2 Different Points of View

In this ﬁeld of application, we have to keep in mind

that the ﬁnal user as well as the main expertise con-

tributor is a surgeon who is not necessarily a specialist

in computer programming. So the description of the

rules of the intervention, and the visualization, have

to be adapted to the surgeon’s vocabulary and habits.

Another point of view is the solver’s one: we have to

provide our solver with a language and some data it

is able to understand. A third point of view concerns

the visualization. The computer needs useful under-

standable information for a proper display. Therefore,

various points of view coexist, and it is necessary that

the application deals with them.

3.3 Analysis of Knowledge

Many procedures involving the placement of one or

more tools that can be assimilated to rays, with the

aim of reaching and treating a target, have a lot of

common points in their planning procedures. The

two main similarities are the deﬁnitions of what

constitutes a tool and what is a solution. We will

illustrate our explanations with different examples:

placement of needles for RFA and cryoablation, and

DBS electrodes.

Deﬁnition. A tool is deﬁned by 3 features: its

geometrical shape, the geometrical shape of the effect

it produces, and the relative placement of the shape

of the effect according to the shape of its support.

For instance the cryoablation’s tool is a needle, its

effect is ellipsoidal and is centered at the location of

the decompression chamber. All other information on

the tool can be deduced from these 3 data.

The expert describes the tool with a speciﬁc

terminology, for example “needle”, “electrode”, etc.,

and is able to make an approximative description of

the effect. He can use either a geometric vocabulary

like “cylindric shape, with a length of 5mm and

a section of 3mm”, or a more fuzzy vocabulary

such as “the effect looks like an olive”. The solver

and the visualization module need a more concrete

description of the tool and its effect, such as sets

of voxels or meshes. Therefore all the information

about the tool have to be collected, or deduced one

from the other in any way.

Deﬁnition. A solution is a placement of a tool. A

placement is composed of a direction (2 degrees of

freedom (DOF)), an origin (3 DOF), and an extra

value, for instance the intensity of the effect (1 DOF).

KEOD 2009 - International Conference on Knowledge Engineering and Ontology Development

444

Table 1: Examples of complex operators, with comprehensive names, and their proﬁles.

lengthOfTool: tool → ﬂoat distToolOrgan: tool * solution * shape → ﬂoat

volumeOfEffect: tool * solution → ﬂoat distEffectOrgan: tool * solution * shape → ﬂoat

centerOfGravity: shape → point coverZoneOrgan: tool * solution * shape → bool

dist2Pts: point * point → ﬂoat toolInsertionPoint: shape * solution → point

Table 2: Our current geometric universe.

Types Examples

point insertion point, intersection organ/tool

shape organ, zone of effect

tool electrode, needle

solution possible solution, optimal solution

For RFA, a solution is a position of the tip of a nee-

dle, a direction of the main axis of the needle, and the

power sent by the generator (size of the effect).

Here again, we have various points of view. The

application (solver and visualization) works with 3D

Cartesian coordinates, whereas the surgeon deals with

various other position references: an insertion point

on the skin, or another coordinate system such as Lek-

sell coordinates in neurosurgery.

Another common point is that all the constraints

we consider are based on the same constants: the im-

ages of the patient, that are segmented providing a set

of organs (3D masks and meshes).

4 GEOMETRIC UNIVERSE

The meta programming approach we chose to use in-

cludes a geometric universe, and operators that can

be combined to deﬁne the geometric constraints rep-

resenting the rules of the surgical intervention.

4.1 Types

As a geometric universe, apart from usual types such

as integers, ﬂoating numbers and booleans, we also

use composed types, as we describe in Table 2. Those

types are used for our constants and unknowns in the

construction of our constraints.

Those composed types allow us to include for

each entity all necessary information for the differ-

ent points of view, and the different uses. For exam-

ple, the “shape” type includes a 3D voxel mask (seg-

mented from CT or MRI images) and a 3D mesh (re-

construction from a mask (organs), or by simple syn-

thesis (effect)). Other properties such as the volume

of a shape, can be deduced from these ones.

4.2 Operators

The differences between each surgical intervention

are the values we give for the elements that deﬁne

a tool, and the constraints to be solved. These con-

straints are expressed under the form of a combination

of (predeﬁned) operators, constants, and unknowns.

We currently use very basic operators (such as plus,

minus, multiply, and, or, etc.) as well as complex op-

erators like the ones shown on Table 1. The terms

that are formed using those operators and the con-

stants can directly be written in the XML ﬁle describ-

ing the surgical intervention, that can be read by the

interpreter.

5 APPLICATION TO

RADIOFREQUENCY

PLANNING

Our methodology for RFA planning explained in

(Baegert et al., 2007a; Baegert et al., 2007b) was orig-

inally implemented in a speciﬁc solver. In order to

validate our new approach, we transformed our orig-

inal solver into a new generic solver, extracting the

speciﬁc functions and replacing them by generic op-

erators. The solver takes as an input trees of oper-

ators representing constraints, and performs a depth-

ﬁrst solving of the operators. We wrote the constraints

using an XML syntax in a ﬁle dedicated to RFA inter-

ventions. An example of XML constraint is written

in Table 3. In this example, the term constrains the

trajectory (distance from insertion point to target) to

be shorter than the length of the needle.

Finally, we experimented the solver to compare

the solutions. The generic solver was tested on 10

patients cases we had already solved with the original

version, and that were already validated by an expert

(see (Baegert et al., 2007a) for detailed results). The

resolution consists in ﬁnding the optimal position for

the RFA needle, given a 3D scene representing the

patient’s anatomy, and given the constraints ﬁle for

RFA interventions.

As expected, for each tested patient case, the re-

sults are identical in terms of precision of the solu-

tion (identical positions of tool and sizes of effect).

MULTI-SEMANTIC APPROACH TOWARDS A GENERIC FORMAL SOLVER OF TOOL PLACEMENT FOR

PERCUTANEOUS SURGERY

445

Table 3: Example of XML constraint, for Percutaneous RFA treatment.

lower(dist2Pts(centerOfGravity(target), toolInsertionPoint(skin, solution)), lengthOfTool(tool))

</strict constraint>

The reason is that the whole computation operation

used in the solver did not change, we only splitted the

functions into small operators which combination de-

scribed in the XML constraints ﬁle recreates the same

computation scheme. The only difference in the re-

sults is in terms of computation time, that is a little

bit slower with the generic version. We also expected

this result, as an gain in genericity often comes with a

performance loss. However, given that in both cases

the total computation time of this planning process is

performed in an average time of a few seconds (maxi-

mum experimental time for the worst case 2mn.), this

increase in the computation time was considered as

negligible and perfectly acceptable by the surgeons.

6 FUTURE REQUIREMENTS FOR

MODULARITY

We presently dispose of a tested generic solver, di-

rectly able to ﬁnd an optimal placement planning for

RFA, but also for other percutaneous interventions

with very similar tools and processes, if the appropri-

ate constraint ﬁle is written. We are currently working

on the constraint ﬁle for DBS in neurosurgery, with

appropriate validation by experts.

For a more open genericity, we also need in future

works to make sure of more extensions capabilities, in

order to be able to include more surgical interventions

types. We deﬁned 3 categories of extensions, imply-

ing 5 different stages of various level of difﬁculty in

the improvement of modularity of our method: new

constraints using new operators, similar interventions

using more than one needle (e.g. cryoablations), and

interventions having other shapes of effect (e.g. ra-

diotherapy).

7 CONCLUSIONS AND FUTURE

WORKS

We described how we abstracted an existing solver

of geometric constraints aiming at computing auto-

matically an optimal placement of surgical tools for a

speciﬁc intervention, to obtain a generic solver. We

implemented a system loading a ﬁle describing the

constraints of the surgical intervention for which a

planning is required. The use of meta-programming

allows us to describe the geometric constraints rep-

resenting the rules of the surgical intervention with

a language more accessible than a programming lan-

guage, and with a geometric universe and operators

that could be redeﬁned on the ﬂy in the future.

Further works remain to be done in order to be

even more generic and to extend to more surgical

interventions. This study showed us that it will be

feasible in a reasonable time, and with a reasonable

amount of work. Besides the future extensions of the

solver, we will also have to write the constraints of the

other aimed surgical interventions, and validate them

with experts.

REFERENCES

Adhami, L. and Coste-Mani

ere, E. (2003). Optimal plan-

ning for minimally invasive surgical robots. IEEE

Transactions on Robotics and Automation : Special

Issue on Medical Robotics, 19(5):854–863.

Altrogge, I., Kr

oger, T., Preusser, T., B

uskens, C., Pereira,

P., Schmidt, D., Weihusen, A., and Peitgen, H. (2006).

Towards optimization of probe placement for radio-

frequency ablation. In MICCAI’2006, volume 4190

of LNCS, pages 486–493.

Baegert, C., Villard, C., Schreck, P., and Soler, L. (2007a).

Multi-criteria trajectory planning for hepatic radiofre-

quency ablation. In MICCAI’2007, volume 4791 of

LNCS, pages 584–592.

Baegert, C., Villard, C., Schreck, P., and Soler, L. (2007b).

Trajectory optimization for the planning of percuta-

neous radiofrequeny ablation on hepatic tumors. Com-

puter Aided Surgery.

Brunenberg, E., Vilanova, A., Visser-Vandewalle, V.,

Temel, Y., Ackermans, L., Platel, B., and ter

Haar Romeny, B. (2007). Automatic trajectory plan-

ning for deep brain stimulation: A feasibility study.

In MICCAI’2007, volume 4791 of LNCS, pages 584–

592.

Lung, D., Stahovich, T., and Rabin, Y. (2004). Comput-

erized planning for multiprobe cryosurgery using a

force-ﬁeld analogy. Computer Methods in Biome-

chanics and Biomedical Engineering, 7(2):101–110.

KEOD 2009 - International Conference on Knowledge Engineering and Ontology Development

446