
REDUCED IMPLICATE TRIES AND LOGICAL OPERATIONS
∗
Andrew Matusiewicz, Neil V. Murray
ILS Inst., Department of Computer Science, State University of New York, Albany, NY 12222, U.S.A.
Erik Rosenthal
Department of Mathematics, University of New Haven, West Haven, CT 06516, U.S.A.
Keywords:
Knowledge compilation, Reduced implicate trie, Updates.
Abstract:
The reduced implicate trie (ri-trie), introduced in (Murray and Rosenthal, 2005), is a target language for
knowledge compilation. It has the property that any query can be processed in time linear in the size of the
query. In this paper, conjunction and negation are developed as update operations for ri-tries that do not
require recompilation. Conjunction has been implemented, and experimental results, though preliminary, are
promising. Conjoining a formula to an existing ri-trie by compiling the new formula and conjoining the tries
is generally more efficient than compiling the conjunction of the two formulas.
1 INTRODUCTION
Several investigators have represented knowledge
bases as propositional theories, typically as sets of
clauses. However, since the question, Does N P = P ?
remains open — i.e., there are no known polyno-
mial algorithms for problems in the class N P — the
time to answer queries is (in the worst case) expo-
nential. The reduced implicate trie was developed
(Murray and Rosenthal, 2005) as a solution to a prob-
lem posed by Kautz and Selman (Kautz and Selman,
1991). Their idea, known as knowledge compilation,
was to pay the exponential penalty once by compil-
ing the knowledge base into a target language that
would guarantee fast response to queries. They speci-
fied that the size of the target language be polynomial
in the size of the original theory, and that query re-
sponse time be polynomial in the size of the compiled
theory. The result would then be polynomial response
time to all queries.
The reduced implicate trie (ri-trie) takes a dif-
ferent approach: Admit large compiled theories on
which queries can be answered quickly. It has been
shown that ri-tries guarantee response time linear in
the size of the query. Thus queries of any knowledge
base that can be “practically compiled” — i.e., can be
∗
This research was supported in part by the National
Science Foundation under grants IIS-0712849 and IIS-
0712752.
built in reasonable time and space
2
— can always be
answered quickly.
In this paper, three update operations for the ri-
trie that do not require recompilation are described.
They are negation — i.e., finding the ri-trie of ¬F
from the ri-trie of F , conjunction and union — i.e.,
finding, respectively, the ri-trie of the conjunction and
the union of two ri-tries.
Reduced implicate tries are reviewed in Section 2.
In Sections 3.1 and 3.2, operations on and between ri-
tries are introduced, and in Section 3.4, a preliminary
implementation is described.
2 REDUCED IMPLICATE TRIES
The reader is assumed to be familiar with the terms
atom, literal, clause, conjunctive normal form (CNF),
implicate, and prime implicate. Recall that asking
whether a given clause is entailed by a formula is
equivalent to the question, Is the clause an implicate
of the formula? The reader is also assumed to be
familiar with the trie data structure, which has been
used to represent logical formulas, including sets of
prime implicates (Reiter and de Kleer, 1987). The
nodes along each branch represent the literals of a
2
Reasonable is a subjective term, presumably defined by
the end user.
456
Matusiewicz A., V. Murray N. and Rosenthal E. (2009).
REDUCED IMPLICATE TRIES AND LOGICAL OPERATIONS.
In Proceedings of the International Conference on Knowledge Engineering and Ontology Development, pages 456-459
DOI: 10.5220/0002305204560459
Copyright
c
SciTePress

clause, and the conjunction of all such clauses is a
CNF equivalent of the formula represented by the trie.
A tautology is logically equivalent to the empty
sentence (empty conjunction) and thus has no impli-
cates. A contradiction, on the other hand, is logi-
cally equivalent to the empty clause (empty disjunc-
tion). Thus a contradiction implies all clauses, and the
empty clause is its only prime implicate.
In this paper, we assume that a variable ordering
has been selected, and that nodes along a branch are
labeled consistently with that ordering.
A reduced implicate trie (ri-trie) is a trie whose
branches represent the relatively prime implicates
(Murray and Rosenthal, 2007a): If F is a logical
formula, then a relatively prime implicate is one for
which no proper prefix (with respect to the variable
ordering) is also an implicate. If the leaf node of a
branch in an ri-trie is labeled p
i
, then every extension
with variables of index greater than i is a branch in the
complete implicate trie of F . These extensions corre-
spond to implicates of F that are not relatively prime
and that are represented implicitly by that branch in
the ri-trie.
The ri-trie of a logical formula F can be obtained
with the recursively defined RIT operator, introduced
in (Murray and Rosenthal, 2005).
RIT(F ,V ) =
F V =
/
0
v
i
∨ RIT(F [0/v
i
],V − {v
i
})
∧
¬v
i
∨ RIT(F [1/v
i
],V − {v
i
})
∧
RIT((F [0/v
i
] ∨ F [1/v
i
]),V − {v
i
})
v
i
∈ V
Note that the third conjunct of RIT is RIT of the
disjunction of the first two. As a result, the next
lemma tells us that the branches of the third subtrie
are precisely those that appear in both of the first two.
The notation Imp(F ) is used for the set of all impli-
cates of F .
Lemma 1. Given logical formulas F and G,
Imp(F ) ∩ Imp(G) = Imp(F ∨ G).
Given two formulas F and G, fix an ordering of
the union of their variable sets, and let T
F
and T
G
be the corresponding ri-tries. The intersection of T
F
and T
G
is defined to be the ri-trie (with respect to the
given variable ordering) that represents the intersec-
tion of the implicate sets. The intersection of two tries
(with the same variable ordering) is produced by the
INT operator introduced in (Murray and Rosenthal,
2007b).
Theorem 1. Let T
F
and T
G
be the respective ri-tries
of F and G (with the same variable ordering). Then
INT(T
F
,T
G
) is the intersection of T
F
and T
G
; in par-
ticular, INT(T
F
,T
G
) is the ri-trie of F ∨ G (with re-
spect to the given variable ordering).
Theorem 1 provides a formal basis for a definition
of the RIT operator that produces ri-tries using inter-
section. It is obtained from the earlier definition by re-
placing the third conjunct by INT(RIT(F [0/v
i
],V −
{v
i
}), RIT(F [1/v
i
],V − {v
i
})).
3 UPDATING ri-TRIES
It is typical in the knowledge compilation paradigm
to assume that the intractable part of the processing is
done only once (or at least not very often). In the ab-
sence of an efficient updating technology, this favors
knowledge bases that are stable; i.e., a single compi-
lation is expected to provide a repository that remains
useful over a large number of queries. The original
knowledge base can always be modified and then re-
compiled, but in general this is expensive. As a result,
updates that can be installed into the compiled knowl-
edge base without recompiling have the potential to
widen applicability considerably.
Four update operations for ri-tries were intro-
duced in (Murray and Rosenthal, 2007b): Intersec-
tion, substitution of a truth constant, variable reorder-
ing, and conjunction with a clause. Two update oper-
ations are described in Sections 3.1 and 3.2: negation
and conjunction.
3.1 Negation
The RIT operator by itself produces a trie for a for-
mula F in which every leaf is labeled 0 or 1. Truth
functional simplifications then yield the desired ri-
trie. Without the simplifications, the trie is called a
constant leaf trie (cl-trie). Merely swapping the 0’s
and 1’s in a cl-trie will produce a representation of
¬F , but this is not the cl-trie of ¬F . The difficulty
is the third conjunct. The NEG operator recursively
simplifies the first two conjuncts and then applies the
INT operator to produce the third. Below, the formal
definition of NEG uses the representation of the trie
T rooted at p
i
as the 4-tuple hp
i
, T
+
, T
−
, T
0
i, see
(Murray and Rosenthal, 2007b).
NEGhr,
/
0,
/
0,
/
0i = h¬r,
/
0,
/
0,
/
0i
NEGhr, p,
/
0,
/
0i = hr,
/
0,¬p,
/
0i
NEGhr,
/
0,¬p,
/
0i = hr, p,
/
0,
/
0i
NEGhr, p, h¬p,T
+
,T
−
,T
0
i,h0,T
+
,T
−
,T
0
ii =
hr,
/
0,NEGh¬p,T
+
,T
−
,T
0
i,
/
0i
REDUCED IMPLICATE TRIES AND LOGICAL OPERATIONS
457

NEGhr,hp,T
+
,T
−
,T
0
i,¬p,h0,T
+
,T
−
,T
0
ii =
hr,NEGh¬p,T
+
,T
−
,T
0
i,
/
0,
/
0i
NEGhr,hp,T
+
,T
−
,T
0
i,
/
0,
/
0ii =
hr,NEGhp,T
+
,T
−
,T
0
i,¬p,NEGh0,T
+
,T
−
,T
0
i,i
NEGhr,
/
0,h¬p,T
+
,T
−
,T
0
i,
/
0ii =
hr, p, NEGh¬p,T
+
,T
−
,T
0
i,NEGh0,T
+
,T
−
,T
0
ii
otherwise NEGhr,T
+
,T
−
,T
0
i =
hNEG(T
+
),NEG(T
−
),INT(NEG(T
+
),NEG(T
−
))i
For example, the ri-trie for p ∨ q is shown on the
left In Figure 1, and the cl-trie is on the right. The
constants of the cl-trie are toggled on the left In Fig-
ure 2, and the cl-trie of ¬(p ∨q) is shown on the right.
q
q
p
p
0
1
0
1
q
p
0
Figure 1: The ri-trie and cl-trie for p ∨ q.
q
q
p
p
0
1
0
0
q
q
p
p
0
1
0
0
0
q
Figure 2: Negating the cl-trie for p ∨ q.
Theorem 2. Let T
F
be the ri-trie for formula F un-
der a given variable ordering. Then NEG(T
F
) is the
ri-trie for ¬F .
3.2 Conjunction
Suppose we have ri-tries T
F
and T
G
for formulas F
and G, respectively. We would like to compute the
ri-trie for F ∧ G.
In the case of a conjunction, any implicate of ei-
ther conjunct is an implicate of the conjunction. How-
ever, the conjunction may have implicates that are en-
tailed by neither of the conjuncts. (E.g., f alse is an
implicate of A ∧ A but not of A nor of A.) In general,
the implicates of a conjunction are a superset of the
union of the implicate sets of the conjuncts.
In order to conjoin the ri-tries for formulas F and
G, first suppose that their first two subtries can be con-
joined pairwise. By definition, their intersection must
represent the third subtrie of the ri-trie for (F ∧ G).
This subtrie represents all implicates of (F ∧ G) that
do not contain p.
The operator INT takes two ri-tries as arguments
under the assumption that they have the same vari-
able ordering. The CONJ operator below employs the
same convention and 4-tuple notation.
CONJ(T
F
,T
G
) =
T
G
T
F
=
/
0 ∨ leaf (T
G
)
T
F
T
G
=
/
0 ∨ leaf (T
F
)
hr, B
+
,B
−
,B
0
i otherwise
with r as the root label of both T
F
and T
G
, and
B
+
= CONJ(T
+
F
,T
+
G
)
B
−
= CONJ(T
−
F
,T
−
G
)
and B
0
= INT(B
+
,B
−
)
Theorem 3. Let T
F
and T
G
be the ri-tries for formu-
las F and G, respectively. Then CONJ(T
F
,T
G
) is the
ri-trie for F ∧ G.
3.3 Structure Sharing
It is often convenient to assume that ri-tries are repre-
sented as trees. Consider however, an atomic formula
whose variable has a high index. If the full ri-trie is
represented as a tree, the size is exponential, as can be
seen in the following lemma.
Lemma 2. The ri-trie of a formula F = v
j
with vari-
ables ordered by index has 3
j−1
+
3
j
−1
2
nodes.
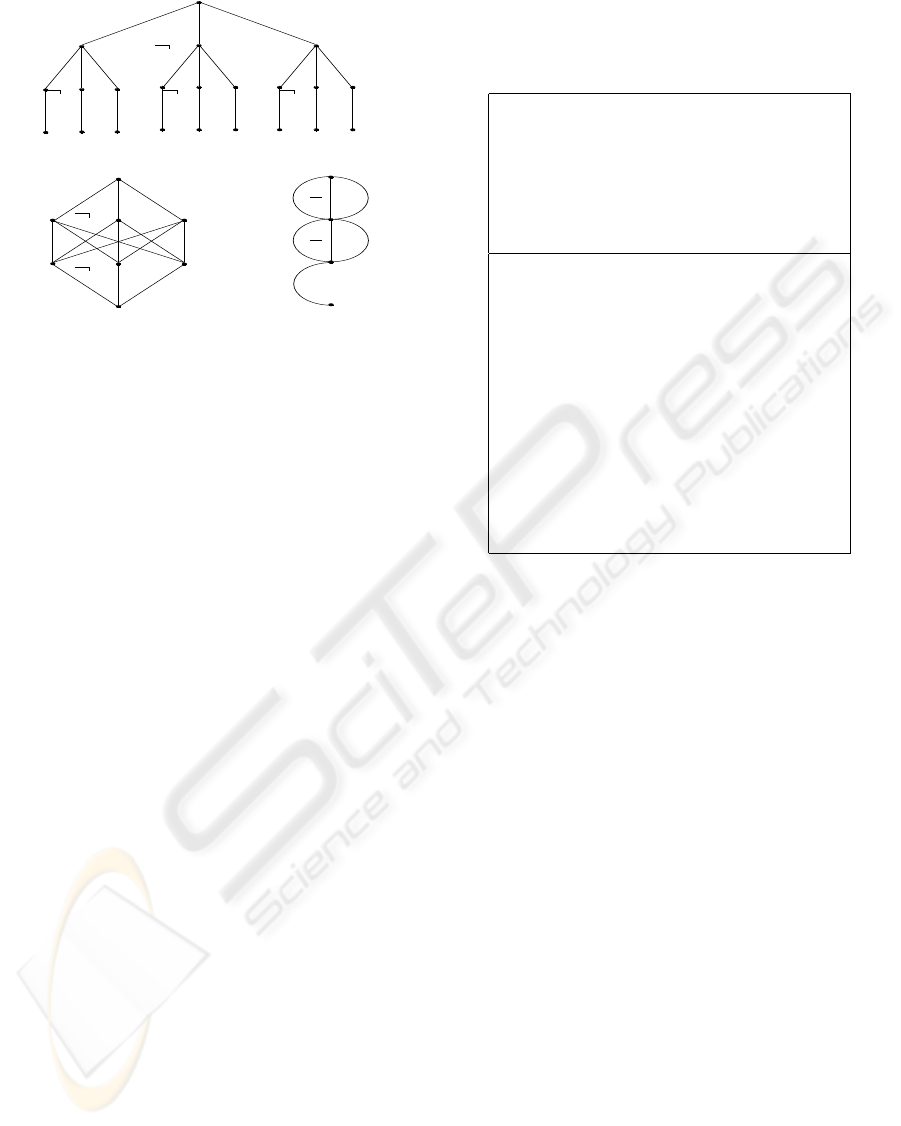
In Figure 3, the ri-trie for v
3
is shown under each
of the three representation schemes discussed in this
section. The variable ordering is by index number.
Structure sharing was applied to all identical sub-
tries in the development of our prototype compiler,
and the resulting reduction in size was orders of mag-
nitude. In some cases, such as that of Lemma 2, this
greedy structure sharing may make the difference be-
tween linear and exponential size.
Lemma 3. The ri-trie of a formula F = v
j
with vari-
ables ordered by index has, under greedy structure
sharing, 3 j + 1 nodes.
Formally, the nodes in an ri-trie are labeled with
literals or the constant 0. The labeling scheme used
in our implementation forgoes node labeling and in-
stead uses edges labeled with ‘+’,‘−’, or ‘0’; variable
indices for the nodes are inferred by the length of the
path traversed in arriving at the node. The root is al-
ways labeled ‘0’. The child of a ‘+’ edge at level j
has an inferred label of v
j−1
, the child of a ‘−’ edge at
KEOD 2009 - International Conference on Knowledge Engineering and Ontology Development
458
v
3
v
0
0
v
2
1
v
1
2
v
0
0
0
+
+
+
1
v
v
1
v
2
v
2
v
2
v
2
v
2
v
2
3
v
3
v
3
v
3
v
3
v
3
v
3
v
3
v
3
v
0 0
0
0
0
Figure 3: The three ri-trie representations for v
3
.
level j has an inferred label of ¬v
j−1
, and the child of
any ‘0’ edge has an inferred label of ‘0’. We will refer
to such a representation as a label-inferred ri-trie.
This convention allows more than just the merging
of identical subtries; subtries that represent distinct
formulas but that are structurally identical can some-
times also be merged. What is required is that one
formula can be obtained by a renaming of the other,
and that the renaming can be done merely by adding
a constant to the indices of all variables.
Lemma 4. The label-inferred ri-trie of a formula
F = v
j
with variables ordered by index, has, under
greedy structure sharing, j + 1 nodes.
3.4 Experiments
The logical operations discussed in Sections 3.1 and
3.2 were added to the prototype compiler. (Disjunc-
tion is provided by the INT operator.) The system
employs greedy structure sharing with label-inferred
ri-tries. In Table 1, each row represents the average
time in milliseconds of five runs involving two ran-
dom 3-CNF formulas over 25 variables.
The first two columns are the number of clauses
in the two formulas. The next three columns are time
in milliseconds for compiling the first formula, com-
piling the second formula and conjoining it to the ri-
trie for the first, and conjoining the two formulas and
compiling the conjunction. The last column is the size
of the compiled ri-trie in nodes.
In all but one case, it is less costly to update the trie
than to recompile with the new formula. The advan-
tage improves as the number of clauses in the first for-
mula increases. The conjecture is that smaller clause
sets are, in a sense, more satisfiable; their ri-tries are
larger, but the cost of computing them is closer to
linear than exponential. Larger clause sets lead to
smaller ri-tries that require much more computation,
compile times increase and update times decrease.
Table 1: Update Experiments
# Clauses, 1
st
formula
# Clauses, 2
nd
formula
Compile time, 1
st
formula
Compile 2
nd
formula
& conjoin
Conjoin both formulas
& compile
# Nodes
40 1 4898 4336 5320 139295
40 5 4754 2722 5702 127324
40 20 4822 4442 4364 70350
50 1 5520 2750 5766 82349
50 5 5538 1408 6294 56549
50 20 5626 2434 4740 12497
75 1 3056 958 2968 14971
75 5 3070 240 3038 8928
75 20 3072 1444 2356 1615
85 1 2244 78 2112 1963
85 5 2276 66 2348 1692
85 20 2260 1360 1794 159
100 1 1886 24 1826 219
100 5 1866 28 1698 79
100 20 1860 1332 1754 8
These results are based on a prototype only and
are very preliminary. But they indicate (not surpris-
ingly) that updating operations are a potentially useful
alternative to recompiling.
REFERENCES
Kautz, H. and Selman, B. (1991). A general framework for
knowledge compilation. In Proc. International Work-
shop on Processing Declarative Knowledge (PDK),
Kaiserslautern, Germany, July, 1991.
Murray, N. and Rosenthal, E. (2005). Efficient query pro-
cessing with compiled knowledge bases. In Proc. In-
ternational Conference TABLEAUX 2005 – Analytic
Tableaux and Related Methods, Koblenz, Germany,
September 2005, pages 231–244. In Lecture Notes
in Artificial Intelligence, Springer-Verlag, Vol. 3702.
Murray, N. and Rosenthal, E. (2007a). Efficient query pro-
cessing with reduced implicate tries. Journal of Auto-
mated Reasoning, 38(1-3):155–172.
Murray, N. and Rosenthal, E. (2007b). Updating reduced
implicate tries. In Proceedings of the International
Conference TABLEAUX 2007 - Analytic Tableaux and
Related Methods, Aix en Provence, France, July 2007,
pages 183–198. In Lecture Notes in Artificial Intelli-
gence, Springer-Verlag. Vol. 4548.
Reiter, R. and de Kleer, J. (1987). Foundations of
assumption-based truth maintenance systems: prelim-
inary report. In Proc. 6th National Conference on Ar-
tificial Intelligence, Seattle, WA, (July 12-17, 1987),
pages 183–188.
REDUCED IMPLICATE TRIES AND LOGICAL OPERATIONS
459
