UNSUPERVISED DISCRIMINANT EMBEDDING IN CLUSTER

SPACES

Eniko Szekely, Eric Bruno and Stephane Marchand-Maillet

University of Geneva, 7 Route de Drize, Geneva, Switzerland

Keywords:

Dimension reduction, Clustering, High dimensionality.

Abstract:

This paper proposes a new representation space, called the cluster space, for data points that originate from

high dimensions. Whereas existing dedicated methods concentrate on revealing manifolds from within the

data, we consider here the context of clustered data and derive the dimension reduction process from cluster

information. Points are represented in the cluster space by means of their a posteriori probability values

estimated using Gaussian Mixture Models. The cluster space obtained is the optimal space for discrimination

in terms of the Quadratic Discriminant Analysis (QDA). Moreover, it is shown to alleviate the negative impact

of the curse of dimensionality on the quality of cluster discrimination and is a useful preprocessing tool for

other dimension reduction methods. Various experiments illustrate the effectiveness of the cluster space both

on synthetic and real data.

1 INTRODUCTION

Data mining and knowledge discovery are concerned

with detecting relevant information or knowledge in

data. Structures or clusters constitute such type of

information and their detection, performed with the

goal of better understanding the data that is being an-

alyzed, represents an active research area of data min-

ing. Therefore two aspects become important here:

structure detection - the algorithms - and structure

understanding - by humans. The importance of both

these aspects has led our work to concentrate on pro-

viding a cluster-driven dimension reduction method

capable of jointly accounting for both these aspects.

Reducing the dimensionality of the data is a prob-

lem that is capturing more and more attention of the

data mining and machine learning communities due

to the necessity of understanding data in ﬁelds like

image analysis, information retrieval, bioinformatics,

market analysis. Dimension reduction is motivated

by: 1) the supposition that data lies in spaces of lower

dimensionality than the original spaces; 2) the need of

reducing the computational load of high-dimensional

data processing and 3) the necessity of visualizing

data.

In many datasets, data is naturally organised into

clusters. Taking the ﬁeld of information retrieval and

givena query, a document’s relevanceto the query can

be associated to the document-cluster membership (a

document is more relevant to a query if it belongs to

the same cluster). In such a context, when reducing

the dimensionality of the data, cluster preservation

becomes critical for efﬁcient retrieval. However, the

preservation of clusters, despite its importance in nu-

merous ﬁelds, has still received only little attention.

1.1 Motivation and Contributions of the

Paper

We consider to be given a set of N data points X =

, x

, ..., x

} that are assumed to come from a mul-

timodal distribution, that is, they are organised into K

clusters.

Problem. We search for a new representation

space S - the cluster space - that can discriminate

and emphasize clusters in case they exist.

Data points are considered to originate from a D-

dimensional space R

where each point x

is rep-

resented by the D-dimensional feature vector x

, x

, ..., x

} for all i = 1..N. Generally, the num-

ber of clusters K is (a lot) smaller than the number of

original dimensions D.

Existing dimension reduction methods are blind

to the structure of the data making identiﬁcation of

clusters in reduced spaces difﬁcult. Nevertheless, the

need for structure preserving during the process of re-

duction is important as, apart from a continuous in-

Szekely E., Bruno E. and Marchand-Maillet S. (2009).

UNSUPERVISED DISCRIMINANT EMBEDDING IN CLUSTER SPACES.

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval, pages 70-76

DOI: 10.5220/0002306500700076

 SciTePress

spection of the reduced space, recovering the struc-

tures existing in the original space is of importance in

a number of applications: medecine (recovering the

groups of diseases), information retrieval (recovering

the groups of information (image, text)) etc.

Therefore, we propose an embedding in the clus-

ter space, where point coordinates are calculated by

means of their relative distances to each of the clus-

ters. The algorithm starts with a ﬁrst step of clus-

tering. Once the cluster information is collected in

the original space using a Gaussian Mixture Model,

the discriminant functions provide the coordinates of

points in the cluster space. Moreover, considering

that the estimation of the GMM parameters is opti-

mal, the cluster space represents the optimal space for

discrimination.

The next section revisits related work. Section 3

formally deﬁnes the cluster space. Experiments on

artiﬁcial and real data and comparisons with other di-

mension reduction methods are described in Section

4. The paper ends with discussions and conclusions

in Section 5.

2 RELATED WORK

Many different approaches were proposed for the em-

bedding high-dimensional data into low-dimensional

spaces. Among the coordinate-based methods, the

linear method of Principal Components Analysis is

the most commonly used. It tries to linearly capture as

much as possible from the variance in the data. Meth-

ods based on pairwise distance matrices were de-

signed either: 1) to preserve as faithfully as possible

the original Euclidean interpoint distances (Multidi-

mensional Scaling (MDS) (Borg and Groenen, 2005),

Sammon Mapping (Sammon, 1969) - which increases

the weight given to small distances) or 2) to pre-

serve non-linear transformation of distances (Nonlin-

ear MDS (Borg and Groenen, 2005)) or 3) to un-

fold data that lies on manifolds (Isomap (Tenenbaum

et al., 2000), Curvilinear Component Analysis (CCA)

(Demartines and H´erault, 1997), Curvilinear Distance

Analysis (CDA) (Lee et al., 2000)).

Manifolds are non-linear structures where two

points, even if close with respect to the Euclidean

distance, can still be located far away on the man-

ifold. Isomap and CDA use the geodesic distance,

that is, the distance over the manifold and not through

the manifold. Both CCA and CDA weight the dis-

tances in the output space and not in the input space

like MDS, Isomap or Sammon Mapping do. Differ-

ent from Isomap, which is a global method, Locally

Linear Embedding (Roweis and Saul, 2000) is a lo-

cal method which tries to preserve the local structure

- the linear reconstruction of a point from its neigh-

bours. Similar to LLE, Laplacian Eigenmaps (Belkin

and Niyogi, 2002) build a neighborhood graph and

embed points with respect to the eigenvectors of the

Laplacian matrix. Stochastic Neighbour Embedding

(Hinton and Roweis, 2002) rather than preserving

distances, preserves probabilities of points of being

neighbours of other points. The methods presented

are not capable of projecting new testing points in the

reduced space, since the embedding has to be recom-

puted each time a new point is added.

In the introduction we discussed the importance

of preserving cluster information in reduced spaces.

Clustering is generally approached through hierarchi-

cal or partitional methods. Hierarchical clustering

generates a tree (a dendrogram) with each node be-

ing connected to its parent and with nodes at lower

levels being more similar than nodes at higher lev-

els. Partitional methods partition the data into differ-

ent clusters by doing a hard assignement - each point

belongs to exactly one cluster. Soft clustering, on the

other side, assigns to each point different degrees of

belonging to clusters. The most common example of

soft clustering is the probabilistic Gaussian Mixture

Model, which assumes that data comes from a mix-

ture of gaussians with different covariance matrices.

The idea of representing points in the space of the

clusters was discussed in (Gupta and Ghosh, 2001)

and in (Iwata et al., 2007). In (Gupta and Ghosh,

2001) the authors propose a Cluster Space model in

order to analyze the similarity between a customer

and a cluster in the transactional application area. The

solution uses hard clustering on different datasets and

then maps the results of the different clustering algo-

rithms into a common space, the cluster space, where

analysis is further performed to model the dynam-

ics of the clients. In (Iwata et al., 2007) a Paramet-

ric Embedding is proposed that embeds the poste-

rior probabilities of points to belong to clusters in a

lower-dimensional space using Kullback-Leibler di-

vergence (here posterior probabilities are considered

to be given as input to the algorithm). Our approach

differs from the above ones in that it proposes a solu-

tion that captures the discriminant information in the

embedding space.

3 CLUSTER SPACE

Let us consider that the dataset is grouped into clus-

ters and model it using a full Gaussian Mixture Model

(F-GMM). F-GMM makes the general assumption

that clusters follow Gaussian distributions and they

UNSUPERVISED DISCRIMINANT EMBEDDING IN CLUSTER SPACES

have different general covariances Σ

GMM models the data as a mixture of Gaussians

of the form:

p(x

) =

∑

k=1

N (x

| µ

, Σ

) (1)

The a posteriori probabilities in the GMM are

given as follows:

p(k|x

) =

N (x

| µ

, Σ

)

∑

N (x

| µ

, Σ

)

(2)

Applying the logarithm to the a posteriori proba-

bilities from (2) gives:

log p(k|x

) = log

N (x

| µ

, Σ

)

∑

N (x

| µ

, Σ

)

= log π

−

log(2π) −

log |Σ

−

− µ

)

−1

− µ

)

− log

∑

N (x

| µ

, Σ

)

(3)

Equation (3) can be related to the quadratic dis-

criminant function (see (Hastie et al., 2001) for the

Quadratic Discriminant Analysis) given by:

) = −

log |Σ

| −

− µ

)

−1

− µ

) + log π

(4)

where π

, µ

and Σ

are estimated from the train-

ing data, in a supervised context, and new (testing)

points are assigned to the cluster for which the value

of the discriminant function δ

from (4) is the highest

according to:

argmax

) (5)

To capture the discriminant information in the di-

mension reduction process, we propose the following

deﬁnition of the cluster space:

Deﬁnition 1. The cluster space is a common space

S = {c

} with point coordinates c

given by the values

of the discriminant functions:

= δ

) (6)

To obtain the values of the discriminant functions

and therefore of the coordinates in the cluster space,

in an unsupervised context, the priors π

, means µ

and covariances Σ

can be estimated with a GMM.

The initialization of GMM may be performed with

any clustering algorithm such as partitional or hier-

archical clustering, graph-based clustering etc. The

quality of the embedding is sensitive to a wrong esti-

mation of the mixture parameters, therefore this ini-

tialisation step is important. Subspace clustering may

be a good choice, especially for high-dimensional

data.

The log-scaling of the probabilities that appears in

the equation of the discriminant function from (4) is

important in the cluster space as it corresponds to the

Mahalanobis distance value D

between each point

and each cluster center:

) = −

log |Σ

| −

− µ

)

−1

− µ

)

| {z }

+log π

(7)

The Mahalanobis distance from a point to a cluster

is the distance of that point to the center of the cluster

divided by the width of the ellipsoid along the direc-

tion of the point. As the Mahalanobis distance takes

into account the shapes of the clusters through the co-

variance matrices Σ

, it is well suited for the cluster

space as it allows the capturing of cluster information

contained not only in the interdistances between clus-

ters but in their shapes too. Thus, a point close to a

cluster in the Euclidean sense may be very far away

in the Mahalanobian sense.

The dimensionality of the cluster space is given

by the number of assumed clusters K. Each point x

is thus represented by K coordinates c

(coordinate

of point x

in dimension k) which correspond to the

distances of the point x

to the center of cluster k.

The cluster space given by equation (6) is the op-

timal space for discrimination in the framework of

QDA given that the parameters of the GMM (π

, µ

and Σ

) are optimally estimated.

The cluster space can also be used as a gauge for

clustering tendency since the more the clusters are

separated, the larger the distances to the other clus-

ters will be. Therefore the density of points around

boundaries is a good indicator of class separability. A

high density indicates a weak separation between the

clusters, a low density indicating a high separability.

Thus, further algorithms may be designed that use the

cluster space as a mean for cluster tendency evalu-

ation by analyzing the distribution of points around

boundaries.

3.1 The Algorithm

The algorithm for ﬁnding the cluster space is pre-

sented in Table 1. The algorithm takes as input the

dataset X and the number of clusters K and provides

as output the new coordinates in the cluster space S .

In Step 1 the priors π

, means µ

and covariances

are estimated using the Expectation-Maximization

(EM) algorithm. The values of the discriminant func-

tions δ

) in Step 2 are given by Equation (7). Fi-

nally, in Step 3, the coordinates of points in the new

space S are given by the values computed in Step 2.

KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval

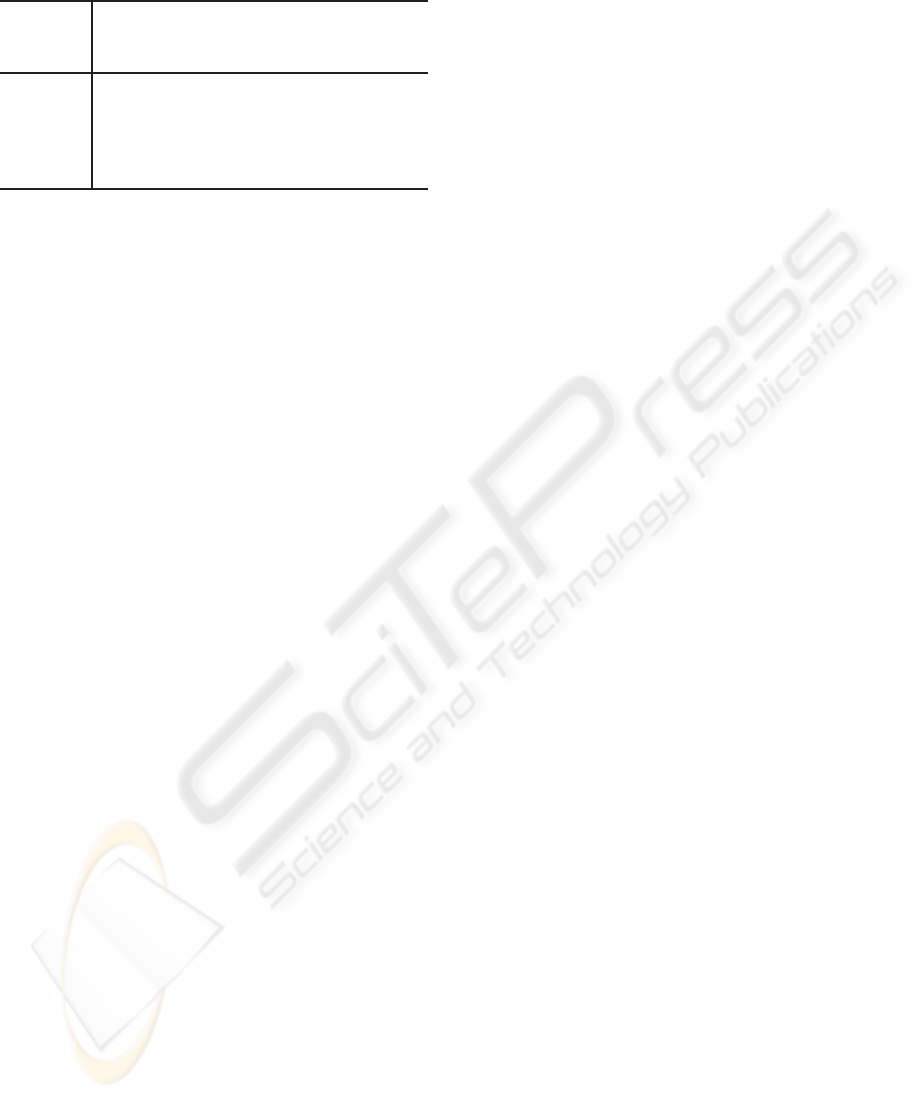
Table 1: The algorithm for the Cluster Space.

Input: X = {x

, x

, ..., x

}, i = 1..N, x

∈ R

K-number of clusters

Output: S = {c

}, i = 1..N, k = 1..K

Step1: Estimate the priors π

, means µ

and

covariances Σ

Step2: Compute the discriminant functions

)

Step3: c

= δ

)

4 EXPERIMENTS

4.1 Artiﬁcial Data

Experiment 1. We generate artiﬁcial data from 3

Gaussians in 3 dimensions as shown in Fig.1. The

Gaussians are given by N

(µ

, Σ

) of 200 points,

(µ

, Σ

) of 200 points, N

(µ

, Σ

) of 200 points

with µ

= [0 0 0], µ

= [1.5 0 0], µ

= [1.5 0 1] and

the covariances:

= Σ





0.01 0 0

0 1 0

0 0 0.01





, Σ





1 0 0

0 0.01 0

0 0 0.01





(8)

Results. We see in Figure 1 that algorithms like PCA

(d) and MDS (f) are not capable of separating the 3

clusters that are well separated in (a). In the cluster

space (b) the clusters are well separated. A further

dimension reduction in this space using Isomap with

a Manhattan distance shows in (c) that the clusters

are separated. Isomap (e) also gives good results but

is dependent on the number of neighbours given to

build the fully connected graph (in such cases - of well

separated clusters - the number of neighbours should

be quite high).

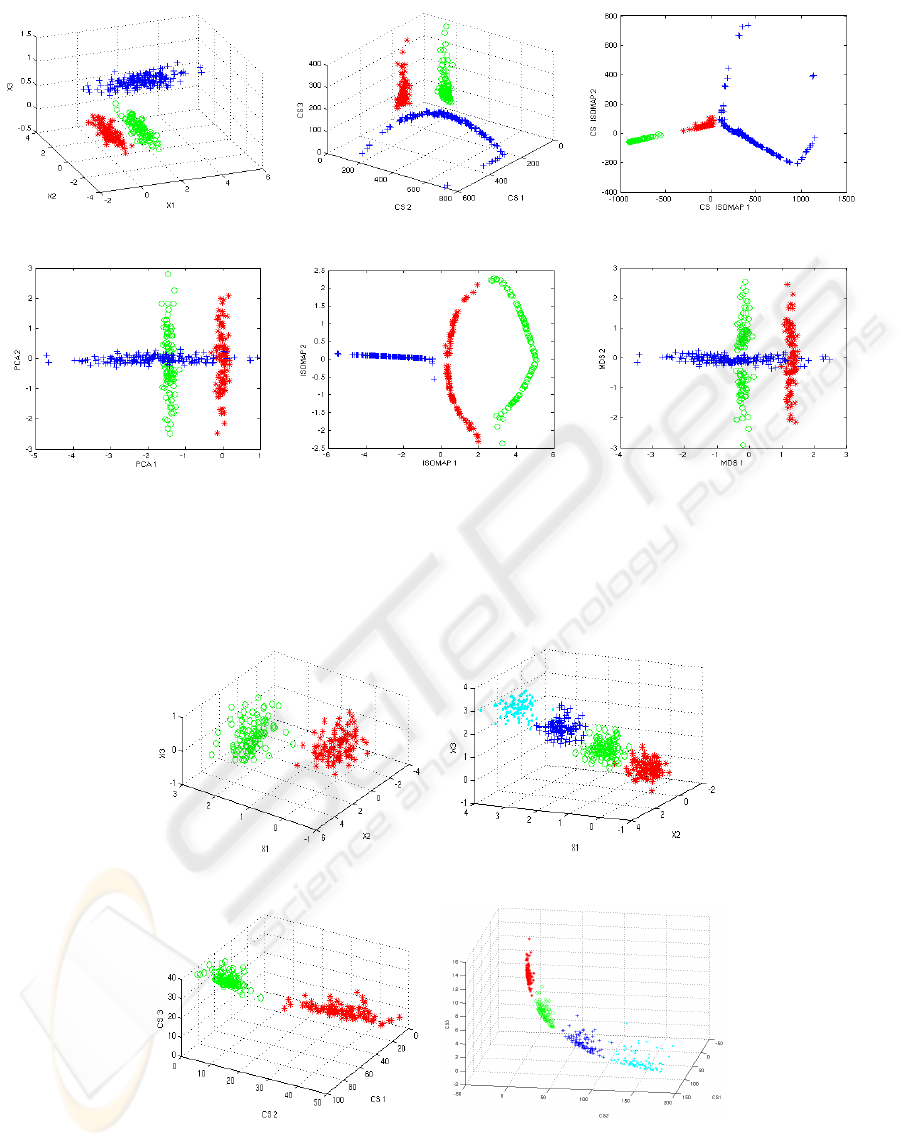
Experiment 2. The choice of K (the number of clus-

ters, and implicitly the dimension of the cluster space)

plays an important role on the quality of the embed-

ding in the cluster space. Figure 2 presents two cases

when the number of chosen K is different from the

number of real clusters in the data. The goal is to

conﬁrm that the choice of K does not force unclus-

tered data to be clustered. K is kept ﬁxed (K = 3) and

the number of clusters varies. We chose K = 3 to be

able to visualize the results in a 3D space.

Results. In the ﬁrst example of Figure 2, (a) and (c),

K is higher than the number of clusters and we ob-

serve that a higher K does not force clusters to break.

This is an important aspect since the embedding, even

if based on an initial clustering, should not artiﬁcially

create structures that do not exist inside the data itself.

Using a soft clustering like GMM avoids forcing clus-

ters to break, like it would happen in a hard clustering

approach (k-means). In the second example, (b) and

(d), K is lower that the number of clusters and we

observe that two of the clusters are embedded in the

same plane but they are however kept separated. In

conclusion, the choice of K is important but a num-

ber of situations work well even with different val-

ues. However, as observed during experimentation, a

lower K inﬂuences more drastically the quality than

a higher K, thus using higher estimates for K is pre-

ferred.

4.2 Real Data

Experiment 1. We give a ﬁrst example using the

Wine dataset from the UCI Machine Learning Repos-

itory. The dataset contains 3 clusters with 178 data

points in a 13-dimensional space. The embedding of

the dataset in a 3-dimensional space is showed in Fig-

ure 3. For evaluation we estimated the Mean Average

Precision (MAP), the purity of the clustering obtained

with k-means and the error of the k-Nearest Neigh-

bour with k = 5. Results appear in Table 2.

Results. We observe that the cluster space captures

all clusters well as opposed to other dimension reduc-

tion method like PCA or Sammon. The new represen-

tation space also allows for a clear visualization in a

3-dimensional space.

Experiment 2. One of the main application of the

cluster space can be seen as a preprocessing step

for further data analysis. The cluster space is use-

ful as a preprocessing step especially when a lower-

dimensional space of dimension 2 or 3 is desired for

example for visualization. In this case, a dimension

reduction in the cluster space can be performed us-

ing a metric that preserves the geometry of the clus-

ter space especially cluster separability. To illustrate

this we use a high-dimensional dataset (MNIST digit

dataset originally embedded in a 784-dimensional

space). Features are extracted from the data with PCA

and the dimension reduction methods that we imply in

the following apply in this space. The examples pre-

sented in Figure 4 show that the preprocessing in the

cluster space helps Isomap to separate clusters in the

2-dimensional space.

In high-dimensional spaces, estimating all the pa-

rameters necessary for a full covariance model is dif-

ﬁcult due to the sparsity of the data. Multiple so-

lutions are possible. One is provided by parsimo-

nious models. Multiple parsimonious models have

been proposed with varying complexities according

UNSUPERVISED DISCRIMINANT EMBEDDING IN CLUSTER SPACES

(a) Original data (b) Cluster space (c) Isomap in the CS

(d) PCA (e) Isomap on the original data (f) MDS

Figure 1: Artiﬁcial data from 3 gaussians in 3 dimensions reduced using dimension reduction methods: a) Original data

projected in the 3 dimensions; b) Data projected in the cluster space using an EM with full covariances, K = 3 and the

Euclidean distance; c) Data from b) reduced using Isomap with the Manhattan distance and 30 neighbours to build the graph;

d) PCA in the original space; e) Isomap in the original space with the Euclidean distance and 30 neighbours; f) MDS in the

original space with the Euclidean distance.

(a) Original data - 2 clusters (b) Original data - 4 clusters

Figure 2: Examples on the quality of the embedding in the cluster space for cases when the assumed number of clusters K

(here K = 3) is different from the real number of clusters.

KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval

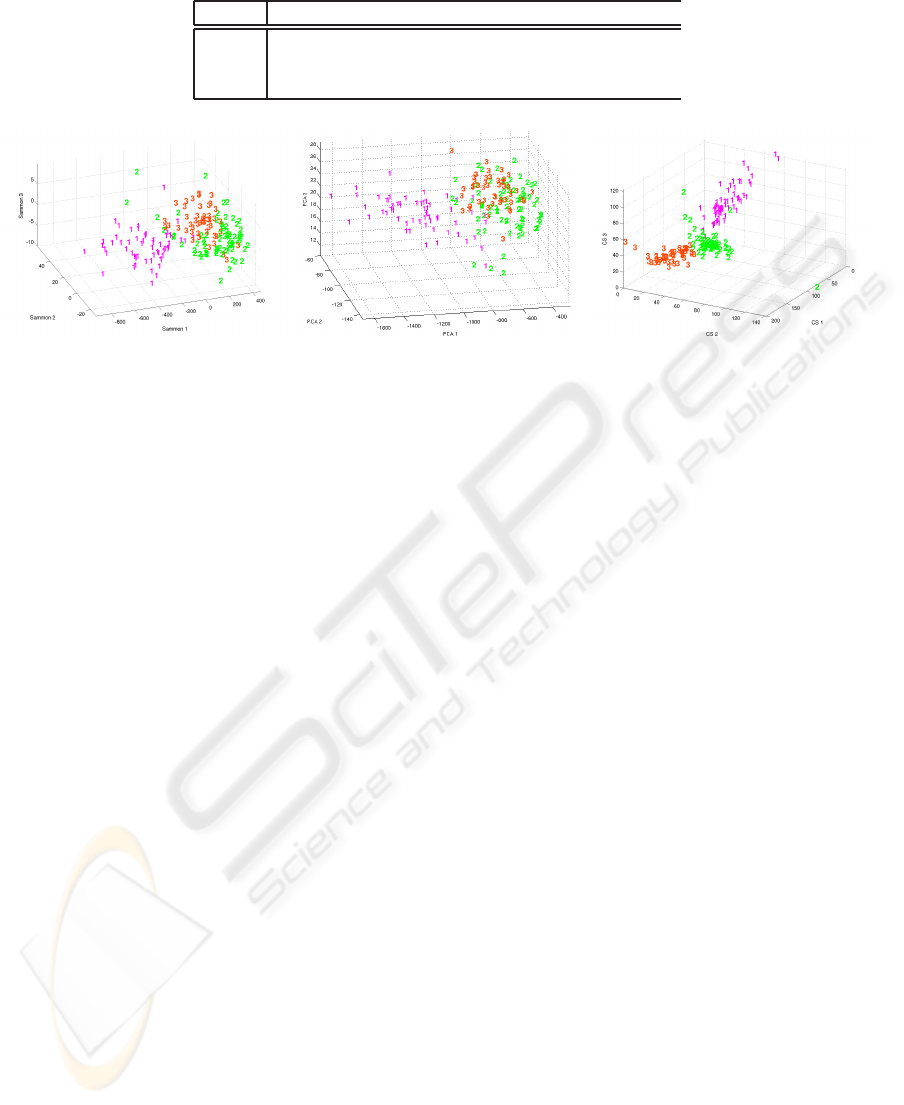
Table 2: Evaluation of the Wine dataset.

Wine Orig PCA Sammon Isomap CS

Purity 67.42 70.22 69.29 69.28 84.83

MAP 0.6433 0.6422 0.6429 0.6424 0.8499

kNN 69.66 69.66 69.66 68.54 94.94

(a) Wine-Sammon (b) Wine-PCA (c) Wine-Cluster Space

Figure 3: Dimension reduction for Wine with different methods.

to the speciﬁc models (intracluster and intercluster)

of the covariance matrices chosen: full different co-

variances, full common covariance, spherical covari-

ance (see (Fraley and Raftery, 2002) for a review). A

second solution is given by truncated Singular Value

Decomposition (T-SVD). The covariancematrix is ill-

conditioned in high-dimensional spaces. The estima-

tion of the inverse matrix can be resolved by using T-

SVD with the ﬁrst t eigenvectors Σ

−1

= U

−1

. A

third solution, that we applied, is possible by ﬁrst de-

noising the high-dimensional data with a method such

as PCA, and further start the analysis in this reduced

space.

5 DISCUSSION AND

CONCLUSIONS

The current construction of the cluster space leads to

the representation of the data in a lower-dimensional

space that emphasizes clusters. However, at least two

issues still need to be addressed to make this construc-

tion generic:

• the presence of clusters is mapped onto the choice

of an initial parameter K, directing both the mod-

eling of the data and the dimensionality of the re-

sulting cluster space. We have shown with differ-

ent experiments (Figure 2) that our process is not

drastically sensitive to a wrong estimation of this

parameter (higher values are to be preferred).

• our model is based on clustering, and therefore the

initialization of cluster centers is very important.

However, due to the sparsity of high-dimensional

spaces, a correct unsupervised initialization re-

mains an open issue. We wish to further inves-

tigate methods for subspace clustering whose per-

formances overcome those of traditional cluster-

ing algorithms as our results in the present reside

on outputs of k-means in the initialization of the

EM.

One advantage of the model is that new points

can be projected in the cluster space (as long as they

do not represent new clusters), their embedding be-

ing computed from the distances to all the clusters.

The model can be further developed to estimate the

parameters of the GMM in a supervised manner.

In this paper, we proposed a new representation

space for embedding clustered data. Typically, the

data is mapped onto the space of dimensionality K

where K is givenby the number of clusters and the co-

ordinates are given by the values of the discriminant

functions estimated in an unsupervised manner. We

call this reduced space the cluster space. This space

is optimal for discrimination in terms of QDA when

the parameters of the GMM are optimally estimated.

The cluster space is a good preprocessing step before

applying other dimension reduction methods. In con-

clusion, the model that we propose is designed with

the goal of embedding data into a low-dimensional

space - the cluster space - where structure is to be

preserved (e.g. cluster emphasis and separability).

UNSUPERVISED DISCRIMINANT EMBEDDING IN CLUSTER SPACES

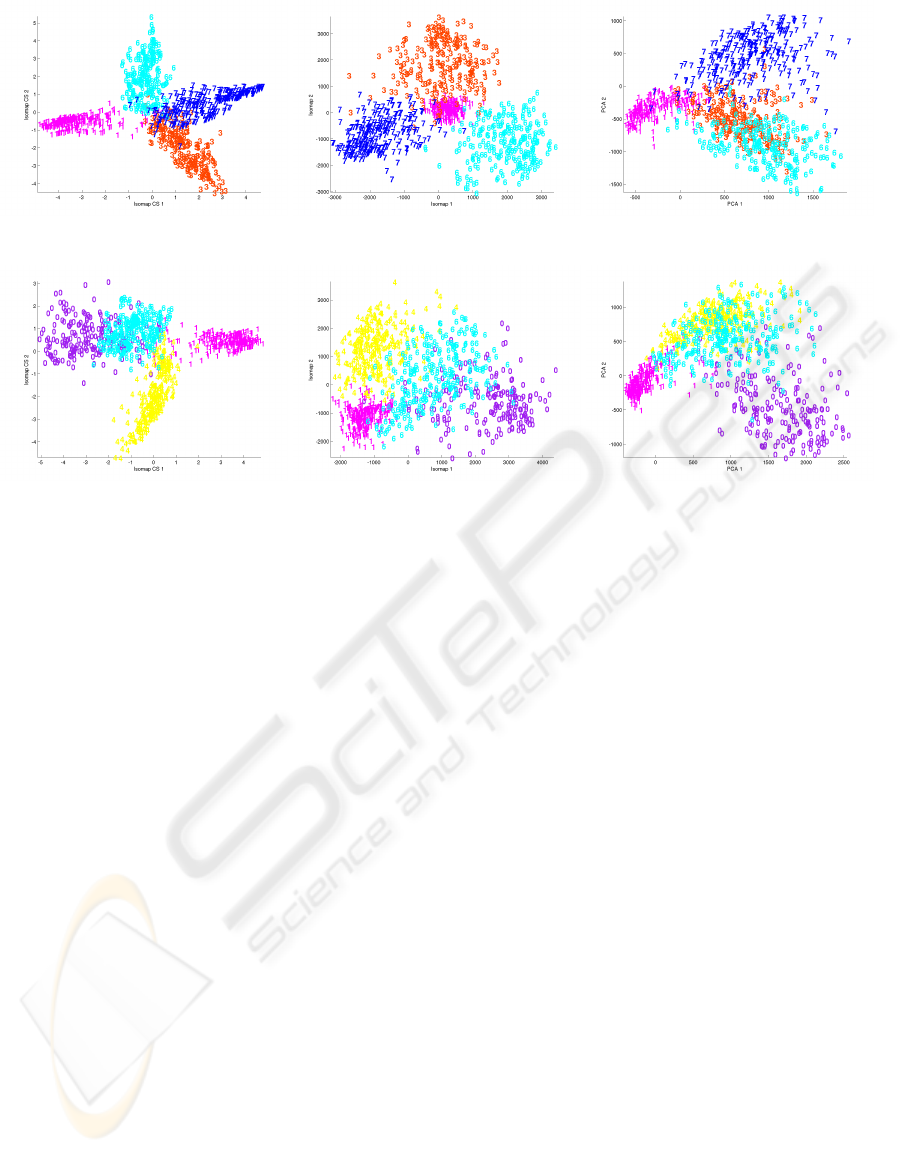
(a) Isomap in the CS (b) Isomap (c) PCA

(d) Isomap in the CS (e) Isomap (f) PCA

Figure 4: Dimension reduction for 1000 MNIST digits (1, 3, 6, 7) and 1000 MNIST digits (0, 1, 4, 6).

ACKNOWLEDGEMENTS

This work has been partly funded by SNF fund

No. 200020-121842 in parallel with the Swiss

NCCR(IM)2.

REFERENCES

Belkin, M. and Niyogi, P. (2002). Laplacian eigenmaps and

spectral techniques for embedding and clustering. Ad-

vances in Neural Information Processing Systems, 14.

Borg, I. and Groenen, P. (2005). Modern multidimensional

scaling: Theory and applications. Springer.

Demartines, P. and H´erault, J. (1997). Curvilinear com-

ponent analysis: A self-organizig neural network for

nonlinear mapping of data sets. IEEE Transactions on

Neural Network.

Fraley, C. and Raftery, A. (2002). Model-based clustering,

discriminant analysis and density estimation. Journal

of American Statistical Association, pages 611–631.

Gupta, G. and Ghosh, J. (2001). Detecting seasonal

trends and cluster motion visualization for very high-

dimensional transactional data. In Proceedings of the

First International SIAM Conference on Data Mining.

Hastie, T., Tibshirani, R., and Friedman, J. (2001). The

elements of statistical learning. Springer-Verlag.

Hinton, G. and Roweis, S. (2002). Stochastic neighbor em-

bedding. In Advances in Neural Information Process-

ing Systems.

Iwata, T., Saito, K., Ueda, N., Stromsten, S., Grifﬁths, T.,

and Tenenbaum, J. (2007). Parametric embedding for

class visualization. Neural Computation.

Lee, J., Lendasse, A., and Verleysen, M. (2000). A ro-

bust nonlinear projection method. In Proceedings of

ESANN’2000, Belgium, pages 13–20.

Roweis, S. and Saul, L. (2000). Nonlinear dimensional-

ity reduction by locally linear embedding. Science,

290:2323–2326.

Sammon, J. W. (1969). A nonlinear mapping for data struc-

ture analysis. IEEE Transactions on Computers, C-18.

Tenenbaum, J., de Silva, V., and Langford, J. (2000). A

global geometric framework for nonlinear dimension-

ality reduction. Science, 290:2319–2323.

KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval