TOWARDS A GENERAL TEMPORAL ONTOLOGY FOR

KNOWLEDGE INTEGRATION

Yi Qiang,

Femke Reitsma and

Nico Van de Weghe

CartoGIS Cluster, Department of Geography, Ghent University, Ghent, Belgium

Department of Geography, University of Canterbury, New Zealand

Keywords: Temporal ontology, Fundamental ontology, GTO, OWL.

Abstract: Practically, temporal information is related to every aspect of our world. A temporal ontology may

effectively negotiate the meanings between different time concepts. Though some temporal ontologies have

been developed, their uses are still narrow and cannot apply into a broader range of knowledge domains.

Our work aims to develop a general ontology of time which can negotiate the heterogeneities in different

time conceptualizations. It is not only a framework for annotating everyday temporal terms on the Web but

also lays a foundation for knowledge infrastructures with more domain-specific time concepts.

1 INTRODUCTION

Practically, temporal information can be found in

every aspect in our daily life. However,

heterogeneities in time conceptualizations cause

ambiguities when people are exchanging time-

related information. For example, if you are

searching through the Web for holiday promotions

this summer, errors may occur when searching from

the Northern Hemisphere for countries in the

Southern Hemisphere. Also, temporal information in

ancient documents is recorded using different

calendars and year-marking systems, which may

cause misunderstandings when they are integrated

together. In recent years, the development of

Semantic Web and ontologies has greatly improved

information sharing and interoperation in many

fields such as Web Services interoperation (Traverso

and Pistore 2004), knowledge management (Takeda

2004; Brodaric et al. 2008) and information retrieval

(Jones et al. 2001). Many ontologies have been

developed and proved their advantages in facilitating

the communication between various information

domains (Hiramatsu and Reitsma 2004; Bard et al.

2005; Raimond et al. 2007; Brodaric et al. 2008).

Also, some attention has been paid to developing

temporal specifications or ontologies for temporal

information on the Web, such as KSL-time (Zhou

and Fikes 2000), OWL-Time (Hobbs and Pan 2006),

TimeML specification (Pustejovsky et al. 2003) and

temporal parts of fundamental ontologies (Navigli et

al. 2003; Herre et al. 2006). The most complete

work of temporal ontology is OWL-Time developed

by Hobbs and Pan (2006), which represents the

commonly-used temporal concepts as well as

temporal aggregates composed of simple time

entities. OWL-Time restricted to temporal concepts

that are frequently used in Web content and Web

Services, but is insufficient in representing time

concepts in some particular domains such as

archaeology, geology and music.

The goal of our work is building a General Temporal

Ontology (GTO) in order to overcome this problem.

The idea of GTO is similar to that of most

fundamental ontologies (e.g. DOLCE

, BFO

, GFO

SUMO

) which attempt to describe very general

concepts that are the same across all domains. These

fundamental ontologies are designed for integrating

heterogeneous knowledge coming from different

sources, most of which already involve very basic

temporal portions. Similarly, GTO is also built at the

most general level of abstraction, but particularly for

time conceptualizations (Figure 1). In other words,

GTO can be understood as a temporal portion of a

fundamental ontology. With GTO, heterogeneous

temporal semantics can be negotiated. Extensions or

sub-ontologies can be developed from it in order to

http://www.loa-cnr.it/DOLCE.html

http://www.ifomis.org/bfo

http://www.onto-med.de/ontologies/gfo/

http://www.ontologyportal.org/

275

Qiang Y., Reitsma F. and Weghe N. (2009).

TOWARDS A GENERAL TEMPORAL ONTOLOGY FOR KNOWLEDGE INTEGRATION.

In Proceedings of the International Conference on Knowledge Engineering and Ontology Development, pages 275-280

DOI: 10.5220/0002307402750280

 SciTePress

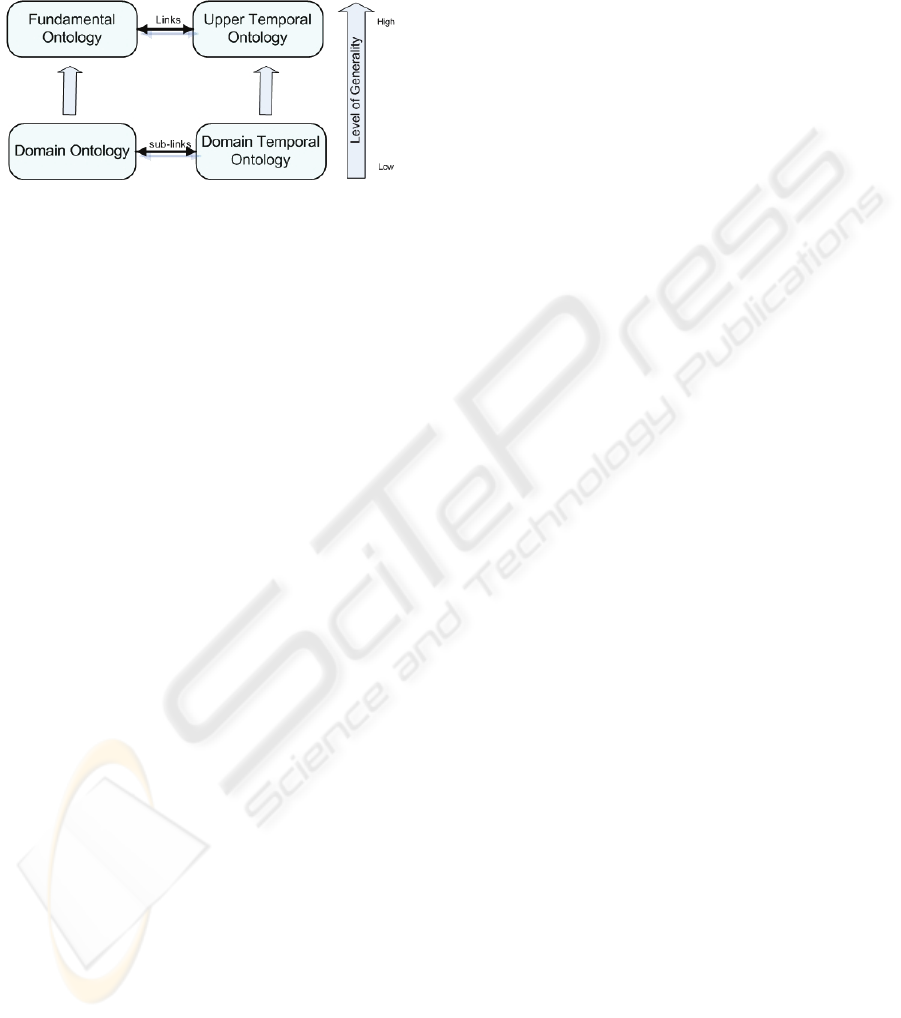
annotate domain-specific time concepts. Since the

goal of our work is implementing GTO with the

most prevalent ontology language (i.e. OWL), the

expressiveness of the ontology is restricted to

Description Logic.

Figure 1: GTO plays similar role as fundamental

ontologies.

The paper is structured as follows: the paper starts

with introducing the basic theories and general

taxonomy of GTO. And then some issues in GTO

have been discussed specifically. Finally,

conclusions are drawn and future work is pointed

out.

2 BASICS OF GTO

2.1 Time Theory Adopted by GTO

Two of the most fundamental questions in building a

temporal ontology are choices of time models and

time primitives. Considering the purpose of GTO is

annotating temporal information rather than

answering complex temporal queries, GTO puts

more emphasis on the representation of temporal

semantics than maintaining reasoning

inconsistencies. GTO is mainly based on the linear

model of time. Cyclic time concepts (such as month,

season, day etc.) are viewed as recurring concepts on

the infinite time line. For example, in the sentence

‘flowers bloom in spring’, ‘spring’ is treated as a

period that regularly reoccurs every year, which is a

kind of non-convex time region in GTO.

In terms of time primitives, GTO adopts both time

instant and time interval. The relation and distinction

between time interval and instance are always

controversial. In one view, a time instant is

considered as an infinitesimal point which is only

used in dividing two time intervals. In the other view,

whether a time region is viewed as an instant or an

interval is a granularity decision that may vary

according to the context of use. A time instant is

undividable and occupies the minimum time unit

under a certain granularity, while a time interval is a

dividable segment of time line and contains more

than one instant. GTO adopts the latter view because

people prefer to use time instants to describe those

instantaneous events such as shooting a gun, turning

off a light. An interval starts at an instant and ends at

an instant, which are called beginning point and end

point respectively. In other words, an interval is

defined by two instants. This time theory may cause

inconsistencies in temporal reasoning such as

Divided Instant Problem (DIP) but is more

expressive in representing temporal semantics in the

natural language.

2.2 Taxonomy of GTO

In many fundamental ontologies (e.g. DOLCE and

BFO), time entities are viewed as regions in time

space, which is the root of temporal concepts.

Convex region and non-convex region are the most

general classes of time regions. Convex regions are

connected and have no gap in it. Non-convex

regions are not connected regions with gaps in it,

which can be further categorized into regular non-

convex regions and irregular non-convex regions.

Non-convex regions are useful in representing time

concepts like ‘the opening hour of the clinic is 9am

to 6pm, from Monday to Friday’. All cyclic time

concepts can be represented by regular non-convex

regions, for example, every spring, every Monday.

Irregular non-convex regions are used to describe

irregularly scattered time regions. Each temporal

region may be described by one or more temporal

descriptions. The general taxonomy of GTO is

illustrated in the form of UML diagram (Figure 2).

With UML diagram, not only the hierarchy of the

ontology is shown, properties, objects of properties

and cardinalities are also shown. Take Instant as an

example, the upper part of the box contains the title

of the class (i.e. Instant), the lower part of the box

contains its properties (DescribedBy) and the object

class (TemporalDescription). The number in []

denotes the cardinality of properties. For example,

[1] denotes that the property has one objects and

[1..] denotes that the property has at least one objects.

For saving space, the diagram only displays some

important properties of classes.

3 ISSUES IN REPRESENTING

TEMPORAL SEMANTICS

GTO aims to providing a general and widely-

applicable framework for representing temporal

KEOD 2009 - International Conference on Knowledge Engineering and Ontology Development

276

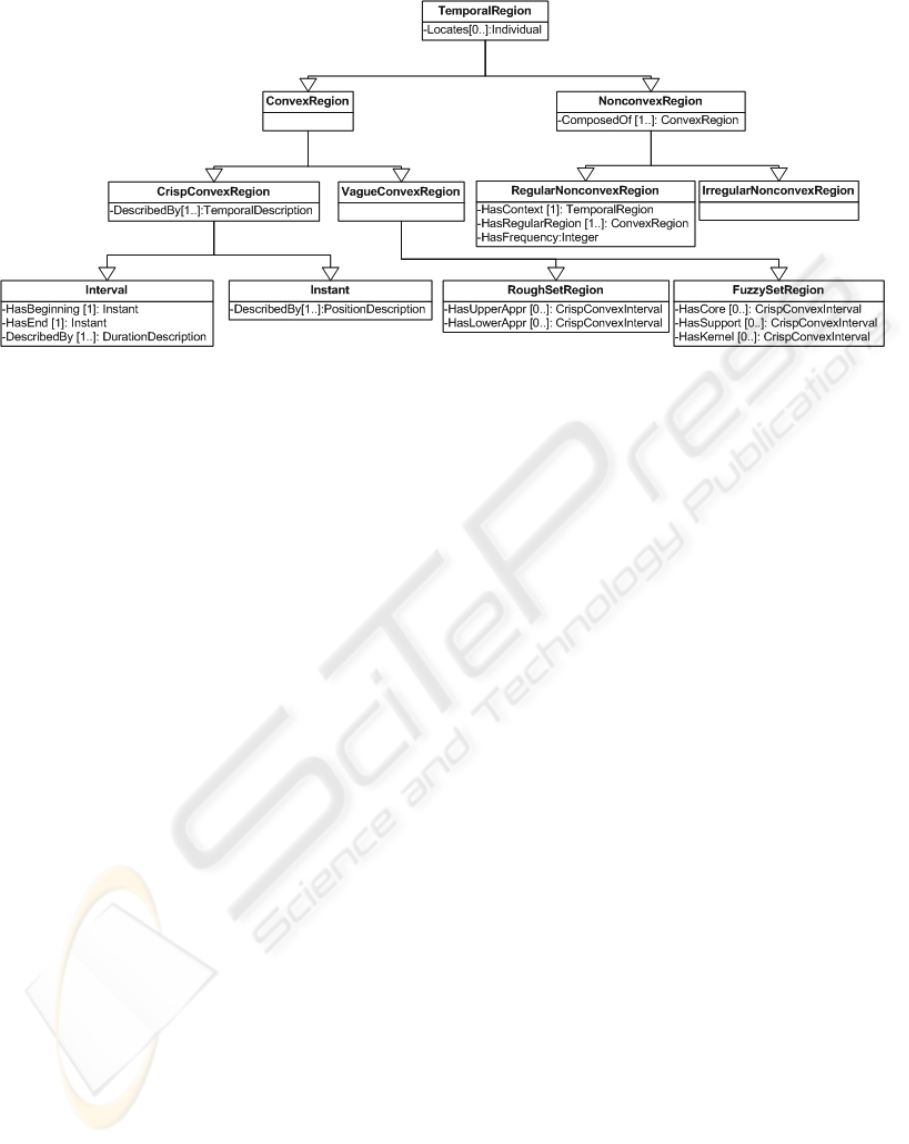
Figure 2: General taxonomy of the temporal ontology.

semantics. We have attempted to make GTO

adoptable to temporal concepts in a broad range of

domains. We adopted merits from relevant work (e.g.

KIF-Time, OWL-Time and fundamental ontologies),

but also posed our solutions on some issues (e.g.

time description, non-convex regions, vague time

regions and links between time and other

individuals). This section discusses about how GTO

solves these specific issues.

3.1 Time Description

Position and duration are the two main properties of

time regions. These two properties can be described

differently. For instance, ‘the first Monday in 2009’

and ‘5

January 2009’ actually point to the same day;

‘7 days’ and ‘1 week’ are intervals of the same

length. Similar to OWL-Time, we defined a class of

temporal descriptions to describe time position and

duration (Equation 1). In this way, time regions may

have diverse position or duration descriptions. We

only create the description class for crisp convex

region (i.e. instant and interval) because all other

time regions can be described by instant and interval

descriptions in some ways. Instants have position

descriptions but no duration description (Equation 2).

Intervals have duration descriptions but no position

description (Equation 3). The positions of intervals

are derived from position descriptions of their

beginning and end instants. Class

TemporalDescription uses integer data properties to

describe time regions. For example, in Figure 2 the

ISPositionDescription (i.e. international standard

time position description) uses properties such as

Year, Month, Date and so on to describe time

positions. For instance, 1

Jan 2009 can be

represented as [Year (2009), Month (1), Date (1)].

However, if you look at some ancient text in China,

time positions and durations are described

differently from that in western world. GTO is also

open for adding classes for such special time

descriptions. Additionally, each position description

has a property HasGranularity to denote the

granularity of the instant.

(,) (, )Describes D T DescribedBy T D

≡

(1)

() () ( )[ (, )

()]

i Instant i p DescribedBy i p

PositionDescription p

∀

≡∃ ∧

(2)

() () ( )[ (, )

()]

I Interval I d DescribedBy I d

DurationDescription d

∀

≡∃ ∧

(3)

Most time regions can be located in the absolute

time line of the real world, in the most common

knowledge, started from the Big Bang and flowing

to the infinite future. But there are some exceptions.

For example, when we say there is a drum beat at

the 13

second in a music track, it is impossible to

locate the drum beat in the time line of the world.

Therefore, we defined a class of time lines where

position descriptions can be located (Equation 4).

Instances of Class TimeLine could be the time line in

a music track, a workflow of automatic control or

the 90 minutes of a football game. Then we are able

to express the temporal semantics in the sentence

like ‘the rocket discard its fuel container at the 15

minute after fire’ or ‘the manager usually substitutes

the No.10 player at the 75 minute in a football game’.

Here actions take place in the time line of the rocket

launching process or the football game.

The taxonomy of temporal descriptions is illustrated

in Figure 3. ISDurationDescription and

ISPositionDescription stand for international

standard time duration description and international

standard time position description respectively.

TOWARDS A GENERAL TEMPORAL ONTOLOGY FOR KNOWLEDGE INTEGRATION

277

More parallel subclasses can be developed at the

same level in order to describe time durations and

positions in diverse time systems.

()[ ()

( )[ ( , ) ( )]]

d PositionDescription d

InTimeLine d s TimeLine s

∀→

∃∧

(4)

Figure 3: The sub-ontology of time descriptions.

3.2 Temporal Relations

In GTO, temporal relations are represented as

properties between classes. Because we take account

of the time granularity, the temporal relations

between time regions under different granularity are

getting complicated. For example, two instants can

only be equal when they not only have the same

position but also have the same granularity

(Equation 5). More complicated situations may arise

for other relations. Considering the purpose of GTO

is not performing complex reasoning about temporal

relations, we only represent temporal relations as

properties between time regions but have not given

complete definitions. This task will be left in the

future work. The thirteen relations between interval

and interval are based on Allen’s model (Allen

1983). Additionally, three relations (before, equal

and after) are defined between instants and instants,

eight relations (before, starts, during, finishes, after

and the inverse ones) are defined between instant

and interval.

1212

11 1

22 2

12 11

22 1 2

() () (, )

(, ) ( )

() (,)

(, ) ( )

Instant i Instant i Equal i i

HasDescription i d PositionDescription d

d d HasGranularity i g

HasGranularity i g g g

∧∧ ≡

∧∧

=∧ ∧

∧=

(5)

3.3 Non-Convex Time Regions

Non-convex time regions have gaps in them. In

other words, non-convex time regions are composed

of many convex time regions. Hobbs (2006) also

proposed representations for this kind of temporal

regions (called temporal aggregate in his work).

However, the representation in GTO is simpler but

more expressive. Non-convex time regions are

categorised into regular non-convex regions and

irregular non-convex regions. Zhou and Fikes (2000)

also used this distinction but gave no concrete

representation for them. Irregular non-convex

regions are composed of irregularly scattered convex

regions. To the contrary, regular non-convex

intervals are composed of regularly scattered regions,

for example, ‘every Monday in May of 2009’ and

‘every Christmas’. In GTO, a regular non-convex

region consists of a regular region and a context

region. The regular region is the regularly recurring

region, while the context region is the range in

which the regular region is recurring. Taking ‘every

Monday during May 2009’ as an example, ‘every

Monday’ is the regular region recurring in the

context region ‘May 2009’. The frequency of the

regular region is set by a float data property (i.e.

HasFreqency). This property is used to describe the

semantics like ‘every other Monday in May of 2009’

where the frequency of the regular region is 0.5.

There may be more than one regular region in a

context region, for example, ‘every Monday,

Wednesday and Friday in May 2009’. Additionally,

context regions can be convex intervals or non-

convex intervals. Non-convex context regions are

used to represent nested regular non-convex

intervals such as ‘every Monday in May’. Here, May

(actually means May every year) is the context

which itself is a regular non-convex interval. Non-

convex regions can be described on the basis of

convex regions. Thus we did not create a description

class especially for non-convex regions. Following

is pseudocode of “every Monday in May”.

EveryMondayinMay

Type: RegularNonconvexRegion

HasRegularRegion: Monday

HasContextRegion: EveryMay

HasFrequency: “1”

EveryMay

Type: RegularNonconvexRegion

HasRegularRegion: May

HasContextRegion: Null

HasFrequency: “1”

May

Type: Interval

HasDescription: 1Month

KEOD 2009 - International Conference on Knowledge Engineering and Ontology Development

278

HasEnd: EndofMay

HasBeginning: BeginningofMay

3.4 Vague Time Intervals

Many domains (geology, history and geography) are

faced with the problem of having vague temporal

information. In these cases, instants have no precise

position and intervals have no precise beginning and

end. This may also refer to the granularity issue. A

crisp time interval may become vague when the

working context shifts from a coarser granularity to

a finer granularity. In GTO, the class of vague

convex regions is used for representing the vague

temporal information (Figure 2). Rough set (Pawlak

1982) and fuzzy set (Zadeh 1965; Pawlak 1982) are

currently the most frequently used theories in

dealing with vague temporal information. The main

difference between them is that fuzzy set has

gradually-changing confidence (between 0 and 1)

according to a function while rough set only has

triplex value (0, 1 or uncertain). In GTO rough set

regions have properties such as upper approximation,

lower approximation whilst fuzzy set regions have

properties such as core, support and kernel (Figure

2).

3.5 Linking Time and Individuals

Because temporal information only makes sense

when it is associated with atemporal individuals (e.g.

process, event or object), it is important to formalise

the links between time and individuals. Currently,

most fundamental ontologies accept the distinction

between endurant individuals and perdurant

individuals, which are called differently in

fundamental ontologies (Table 1). The difference

between endurants and perdurants derives from their

relations to time (Bittner et al. 2004). Endurants are

wholly present at any time they are present, for

example, a book, a lake. Perdurants are wholly

present at any time they are present but extend in

time by accumulating different time parts (Navigli et

al. 2003), for example, a war, a storm. All

individuals are located in time regions that are

similar to spatial locations in the physical space. In

most fundamental ontologies, there is a basic link

between time and individuals (Table 1). For example,

GFO and SUMO only defines the most general link

between time and individual. DOLCE views time as

a subtype of quality like colour, size or weight. This

representation is unintuitive and also problematic

because other qualities also (e.g. colour, size) exist in

time. In our view, both endurants and perdurants are

located in time regions. More specifically, endurants

are wholly present during intervals or present at

instants, whilst perdurants persist during intervals

(e.g. state, process) or happen at instants (e.g. event,

changes). All other specific links between time and

individuals can be developed from them.

Table 1: Distinction of Individuals in Fundamental

Ontologies.

Fundamental

Ontology

Perduring

Individual

Enduring

Individual

Links between Time and

Individuals

DOLCE Perdurant Endurant has-quality (individuals,

temporal-quality)

q-location (temporal-quality,

temporal region)

GFO Process Persential project-to (entities, temporal

region)

BFO Occurrent Continuant N/A

SUMO Process Object when (Individuals, Time)

4 CONCLUSIONS AND FUTURE

WORK

This paper sketched GTO, which is a framework of

an upper ontology for temporal concepts. We

integrated merits from existing temporal ontologies

but also proposed our view on some specific issues

(general taxonomy, time description and non-convex

region, granularity and vague time intervals).

Compared with existing temporal ontologies, GTO

aims to provid a more complete framework of time

abstraction that can be applied into in a broad range

of domains. It not only can annotate everyday

temporal terms on the Web, but can also be further

extended for temporal concepts in particular domains

such as history, geography and archeology. Thus,

GTO may be useful in a knowledge infrastructure

which stores temporal information in different time

systems, for example, cooperating with the SKI

ontology (Brodaric et al. 2008). GTO emphasizes on

the representation of more complete temporal

semantics but ignores some reasoning problems such

as granularity and topological relations.

In the next step, more work is needed for improving

the GTO ontology, including defining temporal

relations, representing more complex non-convex

regions and coupling GTO with fundamental

ontologies. Additionally, some use cases will be

developed to assess the utility of GTO in negotiating

different temporal semantics. Its applications in

knowledge management will be further studied,

which may lay a foundation for a temporally robust

knowledge infrastructure.

TOWARDS A GENERAL TEMPORAL ONTOLOGY FOR KNOWLEDGE INTEGRATION

279

ACKNOWLEDGEMENTS

The research work of Yi Qiang is funded by the

Research Foundation – Flanders.

REFERENCES

Allen, J. F. 1983. Maintaining Knowledge about Temporal

Intervals. Communications of the ACM 26(11): 832-

843.

Bard, J., S. Y. Rhee and M. Ashburner 2005. An ontology

for cell types. Genome Biology 6(2).

Bittner, T., M. Donnelly and B. Smith 2004. Endurants

and perdurants in directly depicting ontologies. AI

Communications 17(4): 247-258.

Brodaric, B., F. Reitsma and Y. Qiang 2008. SKIing with

DOLCE: toward an e-Science Knowledge

Infrastructure. In proceedings of 5th international

conference on formal ontology in information systems,

Saarbrücken, Germany.

Herre, H., B. Heller, P. Burek, R. Hoehndorf, F. Loebe

and H. Michalek 2006. General Formal Ontology

(GFO): A Foundational Ontology Integrating Objects

and Processes. Part I: Basic Principles (Version 1.0),

University of Leipzig.

Hiramatsu, K. and F. Reitsma 2004. GeoReferencing the

Semantic Web: ontology based markup of

geographically referenced information.

EuroSDR/EuroGeographics workshop on Ontologies

and Schema Translation Services. Paris.

Hobbs, J. R. and F. Pan. 2006. Time Ontology in OWL.

W3C Working Draft 27 September 2006, from

http://www.w3.org/TR/2006/ WD-owl-time-

20060927/.

Jones, C. B., H. Alani and D. Tudhope 2001. Geographical

Information Retrieval with Ontologies of Place. In

proceedings of the International Conference on

Spatial Information Theory: Foundations of

Geographic Information Science.

Navigli, R., P. Velardi and A. Gangemi 2003. Sweetening

Ontologies with DOLCE. Intelligent Systems, IEEE

18(1): 22-31.

Pawlak, Z. 1982. Rough Sets. International Journal of

Information and Computer Science 11(5): 341-356.

Pustejovsky, J., J. Castano, R. Ingria, R. Sauri, R.

Gaizauskas, A. Setzer, G. Katz and D. Radev. 2003.

TimeML: Robust specification of event and Temporal

Expressions in Text In proceedings of the IWCS-5

Fifth International Workshop on Computational

Semantics, Stanford, CA.

Raimond, Y., S. Abdallah, M. Sandler and F. Giasson

2007. The Music Ontology. In proceedings of the First

Conference on Social Semantic Web.

Takeda, H. 2004. Semantic web: a road to the knowledge

infrastructure on the internet. New Generation

Computing 22(4): 395-413.

Traverso, P. and M. Pistore 2004. Automated Composition

of Semantic Web Services into Executable Processes.

In proceedings of the 3rd International Semantic Web

Conference – ISWC 2004, Hiroshima, Japan.

Zadeh, L. A. 1965. Fuzzy Sets. Information and Control 8:

338-353.

Zhou, Q. and R. Fikes 2000. A Reusable Time Ontology.

In proceedings of the AAAI workshop on Ontologies

for the Semantic Web

KEOD 2009 - International Conference on Knowledge Engineering and Ontology Development

280