
INTERESTINGNESS – A UNIFYING PARADIGM
Bipolar Function Composition
Iaakov Exman
Software Engineering Dept., Jerusalem College of Engineering, POB 3566, Jerusalem, 91035, Israel
School of Engineering, Bar-Ilan University, Ramat-Gan, 52900, Israel
Keywords: Interestingness, Function Composition, Paradigm, Bipolar, Relevance, Unexpectedness.
Abstract: Interestingness is an important criterion by which we judge knowledge discovery. But, interestingness has
escaped all attempts to capture its intuitive meaning into a concise and comprehensive form. A unifying
paradigm is formulated by function composition. We claim that composition is bipolar – i.e. composition of
exactly two functions – whose two semantic poles are relevance and unexpectedness. The paradigm
generality is demonstrated by case studies of new interestingness functions, examples of known functions
that fit the framework, and counter-examples for which the paradigm points out to the lacking pole.
1 INTRODUCTION
Interestingness is an important criterion by which we
judge discoveries, in particular knowledge
discovery. But, interestingness has eluded all
attempts to capture its intuitive meaning into a
widely accepted formal framework.
There are many proposals for the meaning of
interestingness. Most of them fit our intuition to a
greater or lesser extent. Some of them even correctly
express one aspect or another of what should be
interestingness. Though, none has convincingly
covered the whole issue in a fundamental way.
This work starts with concepts firmly based upon
our intuition to reach a unifying paradigm for
interestingness. It is stated in terms of mathematical
composition of exactly two functions, no less and no
more. It enables grouping apparently disparate
empirical formulas into a common paradigm.
Once its formal framework is made explicit, one
can use it as a guide to propose functions to
calculate interestingness and integrate them into
novel knowledge discovery protocols.
A first example of interestingness composition
involves a matching coefficient of a result as the
relevance to an interest field, multiplied by the
unexpectednes, given by a mismatch coefficient of
the result to the same interest field. It simultaneously
optimizes relevance and novelty of each result.
Moreover, the formal framework serves to check
whether existing functions fit the unifying paradigm,
or it points out to some required kind of addition.
An existing criterion to rank search data is given
by the
TfIdf formula. It perfectly fits the
interestingness paradigm, as our analysis clarifies.
For each of the functions presented, we provide
case studies, in a Web search setting, to demonstrate
that they actually produce interesting results.
The remainder of the paper presents the unifying
paradigm (section 2), introduces match-&-mismatch
as an interestingness function pair (section 3), offers
low-&-high-threshold computational functions
(section 4), shows TfIdf in the new paradigm light
(section 5), and ends with a discussion.
2 INTERESTINGNESS: THE
UNIFYING PARADIGM
Interestingness, within knowledge discovery, is not
an absolute quantity. It is variable along time and
always relative to a field of interest. Here it is argued
that it is bipolar, combining exactly two functions in
a unifying paradigm for interestingness.
2.1 Exactly Two Functions:
Unexpectedness and Relevance
Knowledge discovery means that we acquire new
knowledge that we did not have previously. We use
the term Unexpectedness, rather than the more
neutral novelty, to emphasize that what is new is not
strictly contained in any sense in the previously
196
Exman I. (2009).
INTERESTINGNESS – A UNIFYING PARADIGM - Bipolar Function Composition.
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval, pages 196-201
DOI: 10.5220/0002308401960201
Copyright
c
SciTePress

known.
The very meaning of Unexpectedness, as stated
before, implies that it is relative to previously
existing knowledge. We use the term Relevance,
rather than relativity, to stress that the particular
frame of reference is a chosen field of interest, e.g.
material properties of metals, migratory birds, or
software design patterns.
These two concepts, Unexpectedness and
Relevance, are not just two faces of the same coin,
one relative to the other, but two really independent
functions. Indeed, they are separately quantified.
The previous knowledge exists whether or not
new knowledge is acquired. Thus, the chosen field
of interest can be characterized – say, by some kind
of metadata – before and independently of any
knowledge discovery event. In particular, the
Relevance of any piece of knowledge, say a search
result – be it novel or not – can be quantified relative
to the reference metadata.
New knowledge is not determined by the
previously known. In fact, one can acquire two
pieces of new knowledge, having quite distinct
contents, thus differently quantified, The
Unexpectedness of one of them could be larger than
the other one’s, even with the same previous
knowledge.
The first sense of interestingness is Relevance to
the field of interest. In this sense, an item is
interesting because it fits the field for which one has
a rather stable interest, either professional or
amateur. For instance, metals conduct heat, conduct
electricity and have a shiny appearance. Copper
concerns people interested in metals because it fits
the context metadata.
The second sense of interestingness is
Unexpectedness. In this second sense, an item is
interesting because it calls one’s attention by marked
deviation from the typical item in the context. For
instance, mercury is the only metal which is liquid at
room temperature.
But, mercury is really interesting when one
comes across it, because it is both a typical metal –
conducting and shiny – and has unexpected
properties – a liquid forming spherical drops.
Thus, we really have two functions, viz.
Unexpectedness and Relevance.
2.2 No More than Two Functions
We now argue that there are no more than two
functions related to interestingness.
Suppose that we acquire a new piece of
knowledge that by genetic modification, an
agricultural station has developed yellow tomatoes,
instead of the usual red ones. Yellowness certainly is
a function that can be quantified by colorimetric
methods and by accepted standards.
Should we include yellowness – or for that
matter any other intrinsic property of the new
knowledge – in the calculation of its interestingness?
The answer is negative.
Let us look at the time dependence of
interestingness, after such a knowledge discovery.
At the discovery time, that piece of knowledge has a
certain quantifiable amount of Unexpectedness.
The typical action after knowledge discovery is
to incorporate the new piece into the body of
knowledge available in the respective field of
interest. The Unexpectedness of that piece of
knowledge decreases dramatically. Interestingness
decreases accordingly.
The situation is totally different with yellowness.
A short time afterwards, the yellow tomatoes are still
yellow. The time dependence of yellowness has
nothing to do with one’s knowledge of it.
Obtaining again the same piece of knowledge – a
short time interval afterwards – will not be
considered a discovery anymore. This is analogous
to the registration of a new patent. Once a patent is
registered, its contents are not novel anymore and it
cannot be registered again.
Interestingness – through its Unexpectedness – is
not an intrinsic property of any knowledge piece. It
is a function of the discovery process.
2.3 The Formal Framework
The unifying paradigm for interestingness is
formally expressed by the following equation:
Interest = R
U
(2-1)
where Interest is an expression of interestingness, U
is an Unexpectedness function, R is a Relevance
function,
is the symbol for function composition,
meanimg either mathematical or computational
function composition.
In equation (2-1) one should first apply the
Unexpectedness function on the search results. On
the respective output, one then applies the Relevance
function, in this order. In its most general form,
function composition is not commutative, in analogy
to matrix multiplication.
One could conceivably think of other pairs of
functions for which rather U R is the appropriate
order. But as long as the operator between functions
is
the generic function composition, whatever is
the order it cannot be reversed.
In certain particular cases, composition may be
just multiplicative, and therefore commutative:
INTERESTINGNESS - A UNIFYING PARADIGM - Bipolar Function Composition
197
U *
R = R *
U
(2-2)
Particular cases of importance are selection
functions, that select items from the search result
itemset, by specified criteria.
3 MATCH & MISMATCH
In our first example, a Match coefficient has the role
of a Relevance function and a Mismatch coefficient
is the Unexpectedness function. They are multiplied
as in eq. (2-2) to obtain Interestingness values.
The case study illustrates these functions within
a weblog recommendation system.
3.1 Match & Mismatch Coefficients
The Match coefficient is calculated by comparing
the similarity between the field of interest context
metadata and the current item.
The simplest Match coefficient is a boolean
variable. It has value 1 if at least one keyword is
common to both the field context and the current
item. Otherwise it has a zero value.
A slightly more sophisticated Match coefficient
uses an integer variable. Here one counts the
common words of the context and current item.
A more complex Match coefficient calculation
would involve in some way the edges in the
metadata graph (say an ontology), where the vertices
are keywords.
A Mismatch coefficient counts the dissimilarity
between the field context metadata and the current
item. It is an integer variable.
Assume the field metadata is a set F of keywords
and the current item is a set C. In more precise
terms, the mismatch is calculated as the symmetric
difference of these sets:
Mismatch = F Δ C = (F - C) ∪ (C - F)
(3-1)
Note that mismatch terms can also be weighted,
either by known keyword statistical factors or by the
edges of an ontology graph.
Finally the expression for the Interestingness is:
Interest = Match * Mismatch / NormF
(3-2)
where NormF is a normalization factor that
compensates for differences in the total number of
keywords along result items.
3.2 Case Study: Weblog
Recommendation
This is a case study of weblog recommendation, e.g.
(Fujimura, 2005), (Glance, 2004). The user chooses
a field of interest, here “sports”. A context metadata
is obtained from pre-defined data and user input.
Search was performed with the Yahoo search
engine with the keywords: “Euro 2008 results and
fixtures blog”. Search results were post-processed to
calculate values of Interestingness in equation (3-2).
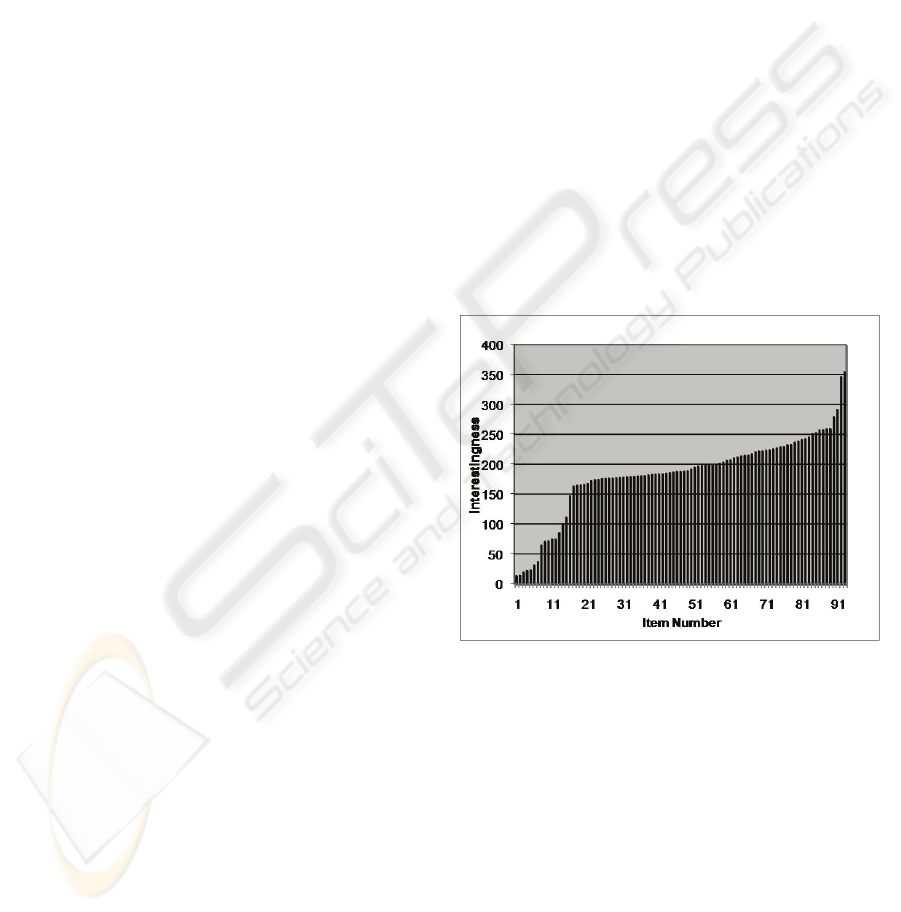
The sorted outcome is plotted in Figure 1.
The outcome is satisfactory for two reasons.
First, there are few “interesting” results, so that one
can make recommendations with confidence. These
are seen in the graph of Figure 1. It clearly
highlights only two results out of 93. One could set a
threshold for automatic decision making.
Second, the Interestingness ranking is
significantly different from the engine search
ranking, which is based on very different
considerations from interestingness. For instance,
the two highest results by interestingness are ranked
by Yahoo search in positions 29 and 67 respectively.
Figure 1: Interestingness plotted against item numbers for
“sports” weblog items. Exactly two items have sharply
higher values (around 350) than others.
4 LOW & HIGH THRESHOLDS
Our second example of interestingness calculation
involves composition of computational functions as
in eq. (2-1). This composition is not commutative.
The low threshold appears within the
Unexpectedness function, while the high threshold is
related to the Relevance function.
KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval
198
4.1 Low & High Computational
Thresholds
The context here is discovery of new keywords. One
first performs regular search in a field of interest for
the user, using a standard search engine.
From the search result item-set one extracts all
the non-trivial words and sorts them by frequency of
appearance. Trivial words are articles, pronouns,
propositions, etc., found in a “stopwords” file.
The Unexpectedness function U outputs all
words below a low-frequency threshold lowT.
These candidate words are then tested by the
Relevance function R as follows: repeat regular
search with the same original keywords and each
candidate word. The candidate is a new keyword if it
is now above a high-frequency threshold highT.
Thus, the interestingness expression in this
example has the same form as equation (2-1):
Interest = R(highT)
U(lowT)
(4-1)
4.2 Case Study: Keyword Discovery
This case study refers to keyword discovery
techniques, see e.g. (Arimura, 2000), (Moukas,
1997).
Samples of result sets with a size of 100 items
were obtained from Yahoo web search of the
keyword combination “migratory birds water swim”.
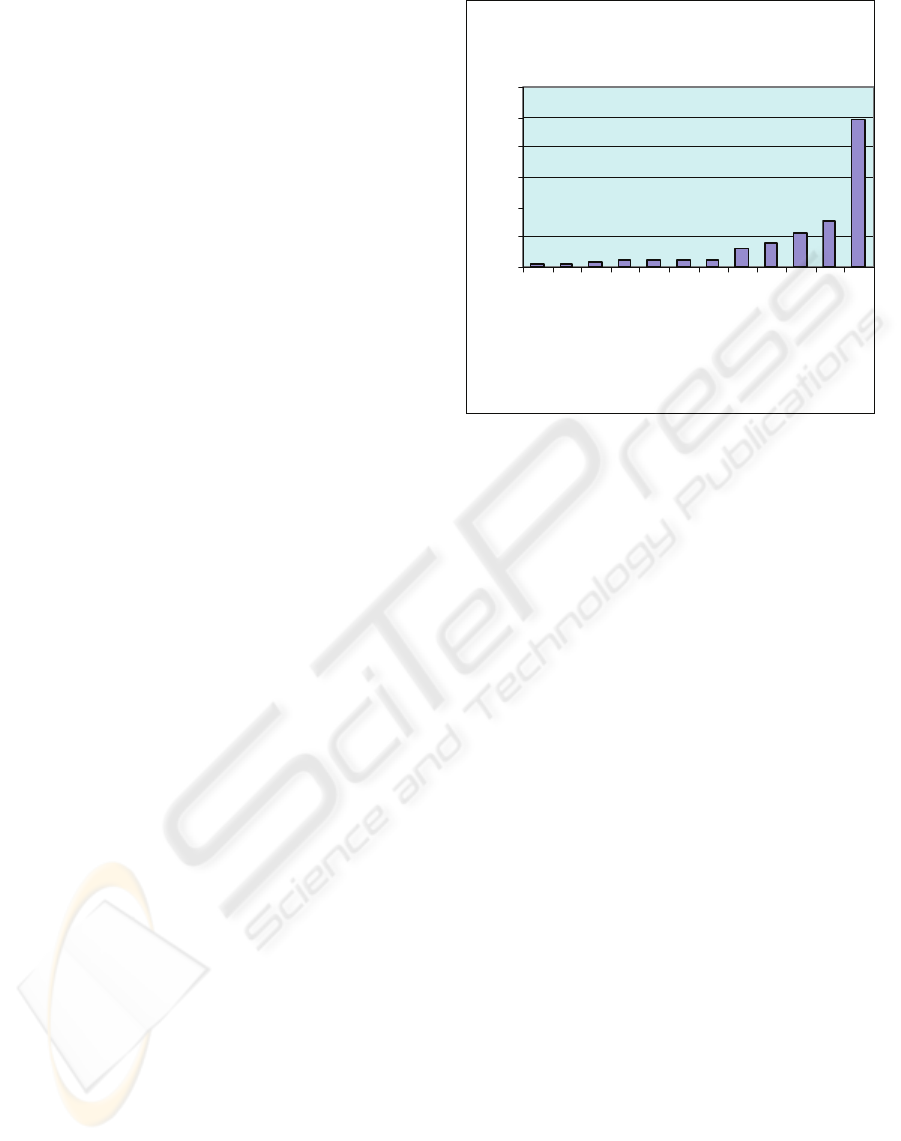
The Unexpectedness function produced among
the numerous low-frequency words appearing only
once the word “phalarope” – previously unknown to
us, as we are not ornithologists.
The Relevance function was applied next, with
the candidate keyword “phalarope” added as input to
the same keyword combination. The outcome shows
this new keyword clearly above the higher threshold.
This is seen in Figure 4.1, for results starting at
result index i=1, up to i=100.
As counter-examples, the same threshold check
for most other low-frequency words does not
succeed.
5 FREQUENCY & INVERSE
FREQUENCY
TfIdf is a well-known ranking criterion for
documents, given keywords of relevance – see e.g.
(Yuwono, 1995). Here it is shown that it perfectly
fits the generic framework for interestingness.
Its application is illustrated in reciprocal mode:
to discover keywords of relevance, when given
interesting documents.
Word Count - 100 Results from 1
0
20
40
60
80
100
120
bi
r
d
s
w
e
bs
ter
tr
i
c
o
l
o
r
b
i
r
dw
e
b
w
at
er
w
ha
tb
i
r
d
ph
al
ar
opu
s
ne
c
k
ed
pr
i
c
eg
r
a
bb
er
w
i
l
s
on
r
ed
p
h
al
ar
ope
Figure 2: Relevance function highlights phalarope – In this
histogram of selected words appearance, the candidate
word is very prominent. Indeed it even appears in two
forms (phalarope, phalaropus).
5.1 Tf for Relevance
The so-called Term Frequency Tf
jk
of keyword k in
document j is:
Tf
j
k
= n
j
k
/ T
j
(5-1)
where n
jk
is the number of appearances of k in
document j, and T
j
, the total number of appearances
of all terms t in document j, serves as a
normalization factor.
Tf
jk
is directly proportional to the number of
keyword k appearances. When k is high-frequency
in documents – as it is typical of keywords used to
characterize a field of interest – the value of Tf
jk
is
accordingly large.
Thus, Tf
jk
has the common behavior of a
Relevance function. It indeed plays this role, when
TfIdf is used to rank documents, with given
characteristic keywords.
5.2 Idf for Unexpectedness
The Inverse Document Frequency Idf of keyword k
is usually given by:
Idf
k
= log (N / df
k
) (5-2)
where N is the total number of documents in the
sub-space under consideration and df
k
is the number
of documents containing keyword k.
Idf
k
is inversely proportional to the number of
documents of interest. The value of Idf
k
increases
INTERESTINGNESS - A UNIFYING PARADIGM - Bipolar Function Composition
199

when there are fewer documents containing the
keyword k, rewarding document rarity. With this
respect, the logarithm serves as a scaling factor,
which does not change the Idf
k
meaning.
Thus, Idf
k
plays the role of an Unexpectedness
function within the TfIdf criterion.
5.3 Interesting Uses of TfIdf
TfIdf has the form of a multiplicative composition,
of the type of eq. (2-2):
TfIdf = Tf
j
k
* Idf
k
(5-3)
The TfIdf criterion is bipolar since it has exactly
two functions pulling frequencies in opposite senses.
The common use of TfIdf is that of a ranking
criterion for documents of interest, given keywords
of relevance.
But, TfIdf can also be used the other way round.
If TfIdf is indeed a valid criterion for interesting
documents, given those documents it can be applied
to find keywords which characterize the chosen field
of interest. This is illustrated in the next case study.
5.4 Case Study: Finding Keywords of
Relevance
This case study refers to software reuse of models
and code found in the Web. In particular we were
interested in cases that combine two design patterns,
such as Observer and Mediator in the same code.
Search with the Google search engine started
with keywords fetched from a target file containing
both general words and keywords associated to
specific design patterns.
Table 1: TfIdf values for Selected Keywords.
Keyword
TfIdf
patterns 14.14
mediator 12.47
concatenate 10.48
observer 6.27
The purpose of the TfIdf calculation was to find
new keywords of relevance to the chosen field of
software pattern reuse. In this context a document is
the title and summary of each item in the search
results. The candidate keywords were all words
appearing in the search results.
Sorting the words by their TfIdf value produced
the outcomes as seen in Table 1 – for a search of
“observer mediator design patterns”.
Although the number of appearances of the word
“observer” is much higher than the word
“concatenate”, TfIdf values reverse their order and
actually highlight new words of relevance, such as
“concatenate”. These new keywords were
incorporated in the target file, for posterior use.
6 DISCUSSION AND RELATED
WORK
The most striking feature of the vast literature on
interestingness that we wish to convey in this very
short literature review is the diversity of concepts
and formulas: a broadly accepted framework is still
lacking.
Deviation – in a statistical sense – has been used
to characterize interestingness for automatic
knowledge discovery in relatively early works – see
e.g. (Piatetsky-Shapiro and Matheus, 1994).
A good source of references is the survey by
Tuzhilin (Tuzhilin, 2000) in the Handbook of Data
Mining and Knowledge Discovery (Klosgen and
Zytkow, 2002), and references therein, e.g.
(Padmanabhan and Tuzhilin, 1999).
Tuzhilin refers to three subjective measures of
interestingness and ways to integrate them.
Unexpectedness is explicitly mentioned. Another
measure, interestingness templates reflects to a
certain extent a form of relevance. The third one,
actionality – another name for usefulness – is
orthogonal to this paper’s claim.
Arimura in reference (Arimura, 2000) uses the
notion of important instead of interesting keywords.
Among other techniques it mentions Shannon’s
entropy as a measure to discover important patterns.
Information entropy is found in a variety of works –
see e.g. (Li, 2006) and references therein.
A more recent survey of interestingness
measures for knowledge discovery is found in
(McGarry, 2005), from which one can infer that
heterogeneity still characterizes the discipline.
6.1 A Unifying Paradigm
Against the background of so much diversity of
content and form, this work offers a unifying
conceptual paradigm of interestingness.
The unifying paradigm has a concise formal
framework. Interestingness is the mathematical
composition of exactly two functions: one standing
for relevance to a chosen field of interest; the other
for the unexpectedness that calls our attention to
specific newly acquired knowledge.
This formal framework is clear enough to enable
judgment relative to our intuitive notions and to the
prevalent trends of research in the area.
On the other hand, the formal framework of this
KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval
200

paradigm is not too restrictive. It encompasses
functions currently used in practice and serves to
stimulate findings of novel functional forms that fit
the paradigm, as discussed next.
6.2 Varieties of Bipolar Composition
To esablish the viability of the unifying paradigm
and its formal framework, it is important to show
that many functional forms obey the paradigm.
We offered three examples, with their respective
case studies: a multiplicative Match*Mismatch
bipolar expression; a non-commutative pair of
computational functions with application of Low
and High thresholds; the well-known Tf*Idf
criterion, which is also multiplicative. Each of them
is bipolar in the sense that they involve exactly two
functions, standing for Relevance and
Unexpectedness.
As a counter-example to stimulate further
research, we mention algebraic similarity vectors.
Any such vector clearly represents the Relevance
side of a possible bipolar expression. By itself it is
not enough to express interestingness as required by
the unifying paradigm.
One could define a kind of dissimilarity vector to
represent unexpectedness, which is a subject for
future investigation.
6.3 Main Contribution
The main contribution of this work is a unifying
conceptual paradigm of interestingness for
knowledge discovery:
-Mathematical composition of exactly two
functions pulling in opposite directions, viz.
Relevance and Unexpectedness.
REFERENCES
Arimura, H. et al., “Text Data Mining: Discovery of
Important Keywords in the Cyberspace”, Int. Conf. on
Digital Libraries: Research and Practice, pp. 220-226,
Kyoto, Japan (2000).
Fujimura, K., et al., “The EigenRumor Algorithm for
Ranking Blogs”, in WWW2005 Conf., Chiba, Japan
(May 2005).
Glance, N. S. et al., "BlogPulse: Automated Trend
Discovery for Weblogs", in WWW2004, New York,
NY USA, (May 2004).
Klosgen, W. and Zytkow, J.M. (eds.), “Handbook of Data
Mining and Knowledge Discovery”, Oxford
University Press, Oxford, Japan (2002).
Li, G, et al., “Shortening retrieval sequences in browsing-
based component retrieval using information entropy”,
J. Systems and Software, 79, pp. 216-230, (2006).
McGarry, K., “A survey of interestingness measures for
knowledge discovery”, Knowledge Engineering
Review J., 20 (1), 39-61 (2005).
Moukas, A., “Amalthea: Information Discovery and
Filtering using a Multiagent Evolving Ecosystem”,
Applied Artificial Intelligence, Vol. 11, Number 5, 1
pp. 437-457 (1997).
Padmanabhan, B. and Tuzhilin, A., “Unexpectedness as a
measure of interestingness in knowledge discovery”,
Decision Support Sys., Vol. 27, (3) (1999).
Piatetsky-Shapiro, G. and Matheus, C.J., “The
Interestingness of Deviations”, KDD-94, AAAI-94
Knowledge Discovery in Databases Workshop (1994).
Tuzhilin, A., “Usefulness, Novelty, and Integration of
Interestingness Measures”, chapter 19.2.2 in reference
[Klosgen and Zytkow], pp. 496-508 (2002).
Yuwono, B. et al., “A WWW Resource Discovery
System”, in 4
th
Int. WWW Conf., Boston, MA., USA
(December 1995).
INTERESTINGNESS - A UNIFYING PARADIGM - Bipolar Function Composition
201
