CHARACTERIZING THE TRAFFIC DENSITY AND ITS

EVOLUTION THROUGH MOVING OBJECT TRAJECTORIES

Ahmed Kharrat, Karine Zeitouni, Iulian Sandu-Popa

PRiSM Laboratory, University of Versailles 45, Avenue des Etats-Unis - 78035 Versailles, France

Sami Faiz

LTSIRS, Ecole Nationale D’ingénieurs de Tunis, B.P. 37, 1002 Tunis-Belvédère, Tunisia

Keywords: Moving object databases, Spatiotemporal data mining, Similarity, Clustering, Density analysis.

Abstract: Managing and mining data derived from moving objects is becoming an important issue in the last years. In

this paper, we are interested in mining trajectories of moving objects such as vehicles in the road network.

We propose a method for discovering dense routes by clustering similar road sections according to both

traffic and topology in each time period. The traffic estimation is based on the collected object trajectories.

We also propose a characterization approach of the temporal evolution of dense routes by a graph

connecting dense routes over consecutive time periods. This graph is labeled by the degree of evolution. We

have implemented and tested the proposed algorithms, which have shown their effectiveness and efficiency.

1 INTRODUCTION

Managing the location of moving objects is an

important issue in several applications mainly in

transport. Some applications meant to monitor and

forecast the traffic use fleets of vehicles equipped

with GPS as probe vehicles, generating Floating Car

Data. In this paper, we focus on moving objects

(MO) that follows a (road) network - so-called

network constraint MO- predominant is real world.

An effective and scalable analysis of such large size

dataset is a great challenge today. This has

motivated research on spatio-temporal data mining

aiming at discovering meaningful knowledge from

this MO data. Trajectory clustering (Lee et al., 2007)

is part of these researches and is one subject of this

paper. The other part is the use of the clusters in

assessing the traffic density and tracking its

evolution over the time. Indeed, with the predictable

availability of trajectory databases, we believe this

could be a better alternative to the analysis of other

traffic sounders (such as under-the-road magnetic

field sensors). First, it covers all the roads. Second, it

does not require any installation or maintenance on

the road network and then has a minimal cost.

Some approaches exist for trajectory data mining

(Li et al., 2007). However, most of them do not

exploit the topology of the underlying network that

has an obvious impact of the density propagation.

Moreover, they do not account for the evolution of

the density over time. Highlighting this evolution

results in a meaningful knowledge – as far as we

know- has not been peered through before.

Our approach is based on two assumptions: the

first is that knowing the statistics on the traffic

density on the network would enable to orient the

grouping road sections by density resulting in dense

routes, then the second is that the dense routes

interact with each other in time, which may fully

describe the evolution of the network density.

In (Kharrat et al., 2008), we presented a

clustering algorithm applied to road sections in order

to discover dense routes, though without considering

the time aspect. As an extension of this algorithm,

we propose here a method to discover dense routes

by clustering nearby sections that show similar

traffic density for each time interval. The traffic is

assessed thanks to the collected spatiotemporal

trajectories. Moreover, we deal with the time

evolution of dense routes and characterize it through

a labeled graph.

Basically, the main contributions of this paper are

those mentioned below:

− We define some new similarity functions

319

Kharrat A., Zeitouni K., Sandu-Popa I. and Faiz S. (2009).

CHARACTERIZING THE TRAFFIC DENSITY AND ITS EVOLUTION THROUGH MOVING OBJECT TRAJECTORIES.

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval, pages 319-322

DOI: 10.5220/0002309403190322

 SciTePress

− We propose a method to cluster the road sections

based upon the network density statistics. Unlike

some existing work, this clustering takes into

account the orientation of the trajectory. Besides,

this method utilizes the network topology to create

relevant clusters.

− We propose a model to assess the evolution for

dense route pairs at two consecutive time intervals.

− We propose a graph conveying the evolution as a

mean to describe the information in a synthetic

manner and to question the evolution of the density

through the whole network.

The rest of the paper is structured as follows. We

describe a few preliminary concepts in section 2. In

section 3, we present the first step concerning the

clustering of road sections. The second step related

to the evolution graph construction is presented in

section 4. In section 5, we present the result of our

experimental study. Finally, section 6 concludes this

paper and sketches some future orientations.

2 PRELIMINARIES

The representation of the network is given by the set

of road sections. The road section is represented

through a graph NG (N, S). S is the set of directed

segments, where each one represents the smallest

unit of road section. N is the set of nodes, where

each one represents a road junction.

Besides, knowing the set of trajectories, we

compute a matrix of transitions for the road network

at each time interval. This tells how many times the

junction have been taken for each turning movement

(i.e. between each pair of adjacent sections), by

reporting the number of moving objects going from

one section to another at each time interval. This

matrix is denoted M and M(i,j) represents the

number of moving objects passing through S

section S

within the interval It

(n ∈ {1,…,k}, k

stands for the number of time intervals). We also

denote S

the transition (or turning movement) from

to S

We adopt a symbolic representation of the

trajectories as in (Du Mouza C. and P. Rigaux,

2004), (Wan T., K. Zeitouni, 2005). In this model, a

moving object trajectory tr is described by an

identifier (tid) and a sequence of symbols where

each one refers to a road section (S

), followed by a

temporal identifier (t

) referring the time of entry of

the trajectory tid to S

tr = (tid , <(S

), (S

), …, (S

)>) with S

∈ S

The order of symbols in the sequence above shows

the movement direction.

Concerning the similarity measure adopted in

this work, we define the similarity (Trans_sim) at

the level of the network for two adjacent transitions

and S

as the difference of their density values:

While the similarity between nonadjacent

transitions is null:

Trans_sim (S

, S

) = 0 if i≠v and j≠u

(2)

We define another similarity measure between dense

routes (Route_sim). It allows comparing the dense

route. Two routes are considered similar (with a

similarity equal to 1) if they share at least one road

section that corresponds to two successive time

intervals. Otherwise, their similarity is null.

3 SECTION CLUSTERING

We call our proposed algorithm NETSCAN. It

carries out the clustering of dense sections and

incorporates them by forming dense routes. It is

inspired from the density based clustering principle

introduced with DBSCAN algorithm (Ester et al.,

1996), while applying it to road sections. It takes as

input the set of sections that constitute the road

network, the spatiotemporal transitions matrix

associated with each time interval, a density

threshold α and a similarity threshold ε between the

transition densities. NETSCAN finds firstly the

dense transitions, i.e. those having maximum value.

Afterwards, for each dense transition, it groups the

connected segments and transitions that have similar

densities, thus creating dense routes.

The process begins with the transition having the

maximal density. Then, it begins searching the

connected transitions in both ways in order to find

those with a density ε near to the maximal one. To

insure the non reuse of transitions that are included

in dense routes, they are marked at the first

assignment.

The extension of a dense route is done in both

ways if the constraints are verified, i.e., the

candidate transition is only marked if it respects the

α and ε thresholds. The obtained segment clusters

correspond to the densest routes in the network. This

procedure is performed again for each time interval.

The dense routes are represented as a sequence of

segments, the same as with the trajectories. Each

segment is identified by an associated symbol.

Trans_sim (S

, S

)= |M(i,j) – M(j,k)| (1)

KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval

320

4 DENSE ROUTE EVOLUTION

This section presents our second algorithm called

DENSITYLINK corresponding to discovered links

between dense routes on successive periods of time.

Algorithm DENSITYLINK allows characterizing

the evolution of the dense road network. For

example, to reveal displacement, extension,

reduction, appearance or disappearance of density

zones along time. It is based on the dense routes

obtained by NETSCAN algorithm, presented in the

previous section. The algorithm builds a graph G

that binds the dense routes. Two routes are directly

linked in this graph if they share the same route in

the network at consecutive periods. Thus, it is

possible to find the origin of a density zone (in order

to avoid it, for example) or to know its effects in

order to predict the future density. Formally, we

define the evolution graph as a labeled graph

G(C,E,W) where C is the set of nodes, each node is

a dense route (i.e. a cluster of road sections). E is the

set of edges where E = (c, c’) means an evolution

link from c to c’. W is a set of labels w that

represents the evolution weight of edge E.

The algorithm takes as input the set of dense

routes distributed on the different time intervals.

This part will be used to follow the evolution of

these routes during time. It will then seek for each

dense route in a time interval it

those that are

similar in the interval it

n+1

. This similarity is based

on the Route_sim definition given in section 2. The

final result is a density graph where each node

represents a state of a dense route at a given time

interval and each transition represents the passage

from a time interval towards the following interval.

Each transition is labeled by two measurements

concerning the evolution. The first represents the

decrease percentage of road sections, compared to

the previous state and the second is the increase

percentage of road sections. These measurements

indicate the degree of change of a dense route:

extension, reduction, displacement or absence of

change.

5 TESTS AND VALIDATION

The experimentation uses synthetic trajectory data

simulated on real map of a road network, which

have thanks to the data generator of Brinkhoff

(Brinkhoff, 2002). Based on the road network of

San Joaquin (24123 segments of roads and 18496

nodes) and that of Oldenburg (7035 segments of

roads and 6105 nodes), we produced various data

files of moving objects trajectories to these two

roads networks. To show the various densities over

time we divided the whole time interval into five

partitions. We calculated the density matrices for

each data file and each time interval. More precisely,

in each matrix, we count the occurrences of the

moving objects crossing it to calculate the transition

M(i,j). The NETSCAN algorithm was implemented

and tested according to various configurations. We

varied the number of moving objects between 1000

and 10000 for each city network.

We notice that the number of transitions having

a dense traffic (a high value of transitions) is very

limited. Figure 1 shows the concentration of the

traffic road on the Oldenburg network for the first

and the last time intervals. The full number of

moving objects in this case is approximately 3500.

One can visually notice on the figure that the density

decreases while going from the first time interval to

the last one.

a – Time interval 1 e – Time interval 5

Figure 1: Density evolution on the Oldenburg network.

Generally, the density on the network is sensitive to

several criteria. First of all, the number of moving

objects on the network, then, the importance and the

shape of the network, we had to notice a difference

in density by taking the same number of moving

objects, but on two different networks. Indeed,

figure 2 shows that with 1000 trajectories, the

number of dense routes is completely different, in

Oldenburg city this number is 119 and in the San

Joaquin city this number is rather 55. Lastly, the

density also depends on the input parameters chosen

by the user, as shown in the figure 2b. The first

parameter α specifies the minimum required density

in a transition of a route and the second ε specifies

the maximum variation of density between

connected sections.

CHARACTERIZING THE TRAFFIC DENSITY AND ITS EVOLUTION THROUGH MOVING OBJECT

TRAJECTORIES

321

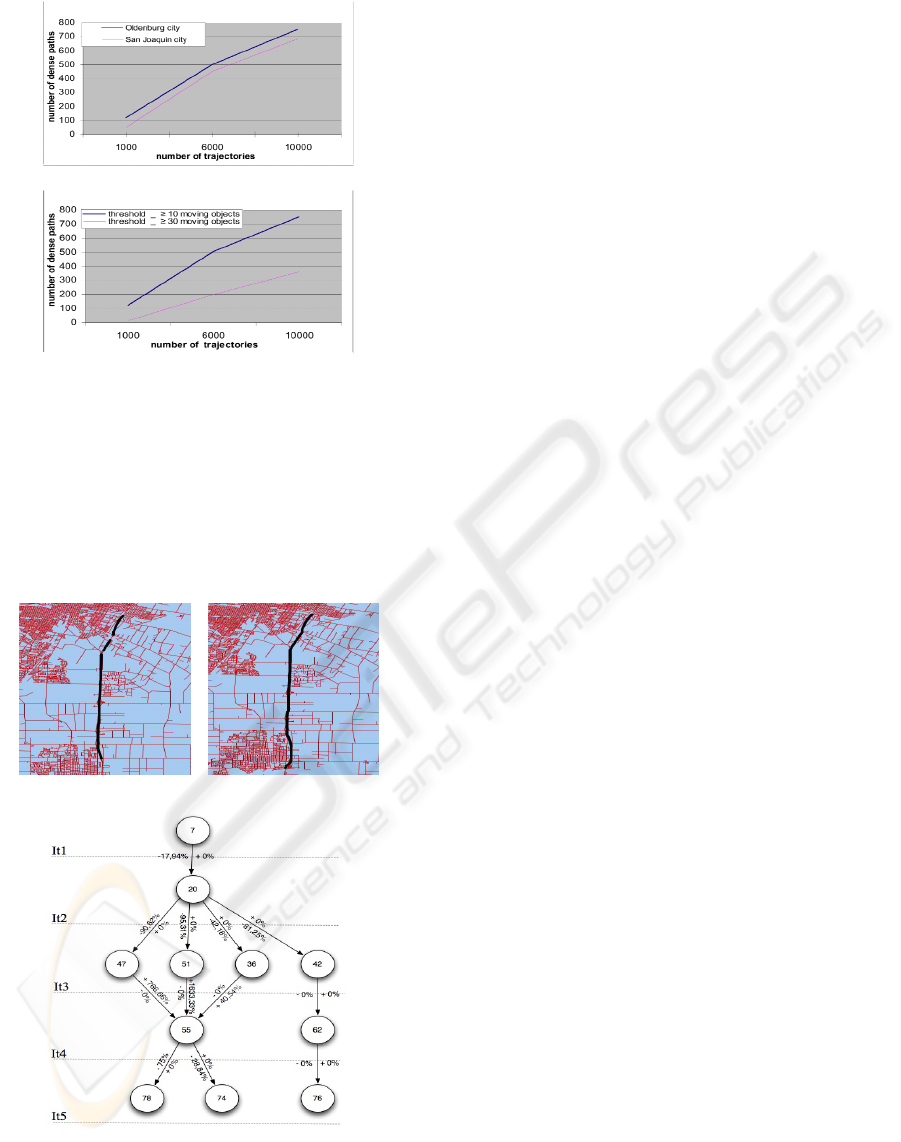
a – Impact of the network on the number of dense routes

b – Impact of parameter α on the number of dense routes

Figure 2: Sensitivity of the dense routes.

By using the same dataset for the two

algorithms, the obtained results in this

experimentation -represented in the form of graphs-

trace the evolution of a dense route through time.

Figure 3 shows the state of a part of the network San

Joaquin during the first (a) and the third (b) time

interval as well as the corresponding graph (c).

a- Time interval 1 b- Time interval 3

c- Evolution graph

Figure 3: Evolution graph starting from the dense route 7.

6 CONCLUSIONS

AND PERSPECTIVES

This paper proposes a new approach for

spatiotemporal data mining. More precisely, it

adapts the clustering density based technique to

network constraint moving objects and organizes the

clusters (dense routes) through a graph of temporal

evolution. This approach performs in two steps. The

first deals with the moving object statistics on the

road network and its topology in order to derive the

densest routes in predefined time intervals. The

second part compares the intersected dense routes in

order to organize them as a graph of density

evolution. In future, we will explore further analysis

of this graph, such as transitive closure to highlight

indirect impact of the density and its propagation in

the network over the whole day. Another issue is to

automatically partition data to relevant time

intervals, and to characterize the periodicity of the

density and its propagation.

REFERENCES

Brinkhoff T., A Framework for Generating Network-

Based Moving Objects, GeoInformatica, Vol. 6, No. 2,

Kluwer, 2002, pp. 153-180.

Du Mouza C. and P. Rigaux. Mobility Patterns. In Proc.

Intl. Workshop on Spatiotemporal Databases

(STDBM'04).

Ester M., H.-P. Kriegel, J. Sander and X. Xu (1996) A

Density-Based Algorithm for Discovering Clusters in

Large Spatial Databases with Noise. In Proc. 2

Int'l

Conf. on Knowledge Discovery and Data Mining,

Portland, Oregon, pp. 226-231.

Lee J-G, J. Han and K-Y. Whang (2007) Trajectory

Clustering: A Partition-and-Group Framework. In

Proc. of SIGMOD'07, Beijing, China.

Kharrat A., K. Zeitouni, I. Sandu-Popa and S. Faiz (2008)

Clustering Algorithm for Network Constraint

Trajectories, In 13th International Symposium on

Spatial Data Handling, SDH, Montpellier, France, pp.

631-647.

Li X., Han J., Lee J. and Gonzalez H. (2007) Traffic

Density-Based Discovery of Hot Routes in Road

Networks. In Proc. of the 10th International

Symposium on Spatial and Temporal Databases

(SSTD), Boston, pp. 441-459.

Wan T. and Zeitouni K., An OLAP System for Network-

Constraint Moving Objects. In Proc. of the 22

Annual ACM Symposium on Applied Computing

(SAC’07), Seoul, Korea, pp. 13-18.

KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval

322