
ARTIFICIAL DATA GENERATION FOR ONE-CLASS
CLASSIFICATION
A Case Study of Dimensionality Reduction for Text and Biological Data
Santiago D. Villalba and P
´
adraig Cunningham
School of Computer Science and Informatics, University College Dublin, Ireland
Keywords:
Dimensionality reduction, One-class classification, Novelty detection, Locality preserving projections, Text
classification, Functional genomics.
Abstract:
Artificial negatives have been employed in a variety of contexts in machine learning to overcome data avail-
ability problems. In this paper we explore the use of artificial negatives for dimension reduction in one-class
classification, that is classification problems where only positive examples are available for training. We
present four different strategies for generating artificial negatives and show that two of these strategies are
very effective for discovering discriminating projections on the data, i.e., low dimension projections for dis-
criminating between positive and real negative examples. The paper concludes with an assessment of the
selection bias of this approach to dimension reduction for one-class classification.
1 INTRODUCTION
Sometimes in practical classification problems we are
given a sample in which only one of the classes, typ-
ically called the “positive” or “target” class, is well
represented, while the examples for the other classes
are not statistically representative or simply do not ex-
ist. That can be the case when the negatives space is
too broad (e.g., the writings of Cervantes against any
other possible writing), when it is expensive to label
the negatives (e.g., multimedia annotation) or when
negative examples have not yet arisen (e.g., industrial
process monitoring). In these cases building a dis-
criminative model using the ill-defined negatives sam-
ple will lead to very poor generalization performance
and therefore conventional supervised techniques are
not appropriate (when usable).
One-class classification (OCC) techniques (Tax,
2001), designed to construct discriminative models
when the training sample is representative of only one
of the classes, emerge as a solution to this kind of
problem. The difference is operational, while the task
is still to accept or reject unseen examples, this can
be done only based on their similarity to the known
positives. Consequently OCC approaches can oper-
ate with no or very few negative training examples,
handling the “no-counter-example” and “imbalanced-
data” problems by considering only positive data.
Many of the domains where one-class classifica-
tion is appealing are characterized by high dimen-
sional datasets. This high dimensionality poses sev-
eral challenges to the learning system and so dimen-
sionality reduction becomes desirable. In this paper
we propose a simple technique that aims to introduce
a discriminative bias in dimensionality reduction for
one-class classification. The algorithm is as follows:
1- enrich the training set by creating a second sample
that will act as a contrast for the actual positives 2- ap-
ply dimensionality reduction in the enriched dataset
and 3- use the low-dimensional representation found
to train a one-class classifier. This idea follows a re-
cent trend in the relevant literature where OCC is cast
as a conventional supervised problem by sampling
artificial negatives from a reference distribution (see
section 3). In this way we try to bridge the gap be-
tween supervised classification and one-class classifi-
cation
However, the gap is wide. Formally when tack-
ling the classification task in a supervised way we
are given a training set Z = {z
(1)
, . . . , z
(n)
} where
z
(i)
= (x
(i)
, y
(i)
) is an input-output pair, x
(i)
∈ X is
an input example and y
(i)
∈ Y is its associated out-
put from a set of classes. Usually X ⊆ R
m
so x
(i)
=
(x
i
1
, x
i
2
, . . . , x
i
m
) is an m-dimensional real vector. Us-
ing Z we infer a classification rule h ∈ H : X → Y
which maps inputs x to predicted outputs h(x) = ˆy ∈
Y . Given the usual 01 loss L
01
(h, x) = I( f (x) 6= y)
we are endeavor to find
ˆ
h that minimizes the risk
202
D. Villalba S. and Cunningham P. (2009).
ARTIFICIAL DATA GENERATION FOR ONE-CLASS CLASSIFICATION - A Case Study of Dimensionality Reduction for Text and Biological Data.
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval, pages 202-210
DOI: 10.5220/0002310202020210
Copyright
c
SciTePress

functional R(h) =
R
L
01
(h, x)p(x)dx. The primary as-
sumption in this learning setting is that Z is represen-
tative of the concept to be learnt, in this case the clas-
sification rule, which means that both the distribution
of the inputs p(x) and the conditional distribution of
the classes given the inputs p(y|x) can be estimated
from Z.
Conceptually one-class classification is very at-
tractive. In practice it is very hard. Due to the absence
of a well-sampled second class, the learning system
cannot get comprehensive feedback and therefore un-
certainty governs the whole process. The fundamen-
tal machine learning assumption that the training set
is representative of the concept to be learnt does not
hold and by definition neither p(x) nor p(y|x) can be
estimated. From an OCC perspective we call the in-
complete information on p(x) the lack of Knowledge
of the Inputs Distribution (KID). The incomplete in-
formation on p(y|x) means we lack an Estimatable
Loss Function (ELF) that might be used in parameter
setting or model selection.
The rest of the paper is organized as follows. In
section 2 we introduce the problem of dimensional-
ity reduction in OCC and describe Locality Preserv-
ing Projections, the dimension reduction technique
we will use in combination with our artificial sam-
ples. In section 3 we present a brief review of the rel-
evant literature for artificial negative generation and
describe four simple strategies for generating artifi-
cial negatives. In section 4 we show the promising
results of our approach in a comprehensive set of text
classification problems and a biological dataset. We
bring the paper to a conclusion in section 5.
2 DIMENSIONALITY
REDUCTION
2.1 Dimensionality Reduction for
One-Class Classification
The curse of dimensionality poses several challenges
for data analysis tools (Franc¸ois, 2008). In practice,
one-class problems are typically of high dimension
so dimensionality reduction (DR) is an important pre-
processing step. In fact, the evaluation on text classi-
fication presented by Manevitz and Yousef (Manevitz
and Yousef, 2001) shows that one-class Support Vec-
tor Machine (SVM) performance is quite sensitive to
the number of features used. This contrasts with two-
class SVMs which are generally considered to be ro-
bust to high data dimensionality. Although the liter-
ature on the topic is quite sparse, it is necessary to
study methods for combating high dimensionally in
the one-class setting.
Using dimensionality reduction prior to one-class
classification should follow this rationale: find a dis-
criminative representation (by feature selection or
transformation) that will improve the classification
performance of the model describing the positive
class. Due to the ELF problem, conventional super-
vised and semi-supervised DR techniques cannot be
used for one-class classification. This is unfortunate
because, clearly, supervision is more effective at dis-
covering discriminative representations. On the other
hand, unsupervised alternatives, relying on assump-
tions like locality or variance preservation, can be ir-
relevant or even harmful for classification, especially
in the absence of actual negatives.
Unsupervised techniques can prove very useful
when their bias are correct for the problem at hand
and are well synchronized with the classifier being
used (Villalba and Cunningham, 2007). Conventional
techniques for unsupervised dimensionality reduction
can do so as a byproduct of the underlying assump-
tions, but the KID problem has an important impact
in their application. For example, consider the case
of principal components analysis (PCA), perhaps the
most popular feature transformation technique. PCA
finds decorrelated dimensions in which the data vari-
ance is large, that is, where the data has a large spread.
Theoretically spreading the data has nothing to do
with finding discriminative directions, yet there are
numerous scenarios where PCA enhances classifica-
tion accuracy. However, based on geometrical intu-
itions and an assumption of solvability for the clas-
sification problem, we can distinguish two different
scenarios when predicting the effectiveness of PCA
for classification – if it has access to positives only or
if it can see both positives and negatives.
This conjecture of solvability is based on this ob-
servation: in the real world, we will usually face types
of classification problems where there will be class
separability in at least some subspace. Often sepa-
rability comes together with high variability between
the classes and so, with a large spread in the whole
data. If projecting into those discriminative subspaces
will spread the data as a side effect, in practice we
can take the reverse path and find high variability sub-
spaces with the hope that they will lead to class sepa-
rability. See figure 1 for a toy example.
On the other hand, in the pure one-class setting,
with no negatives at all at training time, spreading the
data can be regarded as a bad idea. Because of our
total ignorance of the negatives, the approach should
be to maximize the chance that, whatever is their dis-
tribution, we will accept as few of them as possible.
ARTIFICIAL DATA GENERATION FOR ONE-CLASS CLASSIFICATION - A Case Study of Dimensionality Reduction
for Text and Biological Data
203

-5 -4 -3 -2 -1 0 1 2 3 4 5
-10
-8
-6
-4
-2
0
2
4
6
8
10
x
1
x
2
86%
-5 -4 -3 -2 -1 0 1 2 3 4 5
-10
-8
-6
-4
-2
0
2
4
6
8
10
x
1
x
2
76%
-5 -4 -3 -2 -1 0 1 2 3 4 5
-10
-8
-6
-4
-2
0
2
4
6
8
10
x
1
x
2
52%
-5 -4 -3 -2 -1 0 1 2 3 4 5
-10
-8
-6
-4
-2
0
2
4
6
8
10
x
1
x
2
63%
Figure 1: PCA over an artificial 2-dimensional example.
We generate three mirroring data clouds by sampling from
Gaussian distributions with diagonal covariance, the vari-
ance in x
1
(“horizontal dimension”) is three times that in x
2
(“vertical dimension”), and the means differ only in x
2
. We
label the central cloud as the positives examples and the up-
per and lower clouds as the negatives, where the total num-
ber of positives and negatives is the same. When computing
PCA only with the positive data, the first principal compo-
nent is x
1
, accounting for a 75% of the variance. This is
clearly a bad option. On the right side of each plot we indi-
cate the direction of the first principal component found by
using both positives and negatives, labelled with the amount
of variance it accounts for. We move the negative clouds
so that they get closer and, eventually, overlap the positive
cloud. In this case PCA finds ”the right direction” until it is
no longer possible to do so because both classes overlap.
This is achieved by projections that make the positive
data occupy as little space as possible (collapsing),
which in PCA corresponds to those explaining less
variance (Tax and Muller, 2003).
In previous experiments with a wide range of high
dimensional datasets, PCA was found, indeed, not
as useful in a setting without actual negatives (Vil-
lalba and Cunningham, 2007). It can still help when
the aim is to reduce the dimensionality while keep-
ing as much information as possible, but the discrim-
inative aspect that emanates from class separability
completely disappears when training with just one
class. Related to the KID problem, the usefulness of
unlabeled data in classification is one of the central
questions of the semi-supervised approach to learn-
ing (Chapelle et al., 2006, sect. 1.2); while in semi-
supervised classification the effect of unlabeled data
can be negligible from a theoretical point of view, un-
labeled data plays a principal role in semi-supervised
one-class classification (Scott and Blanchard, 2009).
2.2 Locality Preserving Projections
In this paper we focus on the interactions between
one-class classification and Locality Preserving Pro-
jections (LPP) (He and Niyogi, 2003). LPP belongs
to the family of spectral methods, where the low di-
mensional representations are derived from the eigen-
vectors of specially constructed matrices. The idea
behind LPP is that of finding subspaces which pre-
serve the local structure in the data. LPP has its roots
in spectral graph theory (Chung, 1997), and the algo-
rithmic details along with the specific setup used in
our experiments are as follows:
1. Construct the Adjacency Graph: let X be the
training set and G denote a graph with n nodes.
We put an edge between nodes i and j if x
(i)
and
x
( j)
are “close”. When mixing with artificial gen-
eration techniques (sec. 3) we use a supervised
k-nearest neighbors approach, where nodes i and
j are connected if i is among the k-nearest neigh-
bors of j or vice-versa and y
(i)
= y
( j)
, that is, we
only allow links between examples of the same
class. We also use self-connected graphs.
2. Choose the Weights for the Graph Edges. W
is the adjacency matrix of G, a symmetric n × n
matrix with W
i j
having the weights of the edge
joining vertices i and j, and 0 if there is no such
edge. In this paper we use the simple approach of
putting W
i j
= 1 when nodes i and j are connected.
3. Eigenmaps. Compute the eigenvectors and
eigenvalues for the generalized eigenvector prob-
lem:
XLX
T
e = λXDX
T
e (1)
where D is a the degree matrix and L is the Lapla-
cian matrix (Chung, 1997). The embedding is de-
fined by the bottom eigenvectors in the solution of
Equation 1.
It can be shown that by solving 1 we find the direc-
tion e that minimizes
∑
i, j
(e
T
x
(i)
− e
T
x
(j)
)
2
W
i j
. This
objective function incurs a high penalty if neighbor
points x
(i)
and x
( j)
are mapped far apart. Therefore
the bias of LPP is that of collapsing neighbor points.
This seems appropriate for one-class classification,
where collapsing the target class so that it occupies
as little space as possible should account for many
“attacking” distributions. LPP can prove effective for
one-class classification in domains with high redun-
dancy and low irrelevancy between dimensions, for
example chemical spectra or data coming from multi-
ple sensors. However, when using LPP with one-class
classification we still miss the discriminative aspect,
so we will be collapsing neighborhoods inside the tar-
get class without necessarily creating a discriminating
representation.
KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval
204

3 ARTIFICIAL NEGATIVES
GENERATION
A possible solution to incorporate a discriminative
bias into OCC is to constrain the nature of the neg-
atives by studying what are the relevant negative dis-
tributions that can appear in practice. In this way, we
could generate artificial negatives (ANG) that could
be used to help train the system. Our data would then
come from a mixture distribution Q :
X ∼ Q = (1 − π)P + πA (2)
where P is the distribution for the positives, A is the
assumed distribution for the negatives and π ∈ [0, 1]
controls their proportion. Paradoxically, with this ap-
proach the distribution we know is that of the nega-
tives while P is to be estimated from data.
This notion of arbitrarily generating negative data
to enable the application of supervised techniques in
unsupervised problems seems very na
¨
ıve, but it is ad-
vocated by well respected statisticians (Hastie et al.,
2001, pg. 449). Recent theoretical studies in one-
class classification also provide justification for this
approach. El-Yaniv and Nisenson study the decision
aspect of one-class classification, when to accept a
new example, in an hypothetical setting where P is
fully known (El-Yaniv and Nisenson, 2006). Using a
game-theoretic, “foiling the adversary” analysis, they
conclude that the optimal strategy to deal with an un-
known “attacking distribution” is to use randomiza-
tion at the decision level (i.e., incorporate a random
element in the classifier outputs). They also justify the
common heuristic of using the uniform for A, when
defining negatives as examples in low density areas of
positives, as a worst-case attacking distribution in this
scenario.
Estimating density level sets has been cast as su-
pervised problems with contrasting examples sam-
pled from a reference distribution (Scott and Nowak,
2006; Steinwart et al., 2005). Again, these are applied
to one-class classification by defining negatives as ex-
amples in low density areas. Related heuristics have
been used in one-class classification for tasks such as
model selection by volume estimation (Tax and Duin,
2002). These use the volume as a proxy to estimate
the error. Other fully supervised approaches for one-
class classification by the generation of artificial neg-
ative samples and the use of supervised classifiers can
also be found in the literature (Fan et al., 2004; Abe
et al., 2006).
3.1 Non-parametric Artificial Negatives
Generation
Actual negatives could live anywhere in the input
space, thus the space of actual classification problems
for a given set of positive data samples is very large.
In high dimensional spaces, we can generate nega-
tives anywhere and the generation method chosen will
bias the resulting classifier. So the question is, what
are appropriate principles to drive the generation pro-
cess?
Ultimately we want to train a classifier that will
be prepared for mischievous and adversarial attacking
distributions of negatives. A principled way to do that
is to try to generate negatives that resemble the pos-
itives - mimicking some aspects found in P - as that
will create hard but solvable problems. By solvable
we mean that there should be a way of discriminat-
ing P from A, while by hard we mean, for example,
looking for boundary cases or for negative samples
in which the correlations between the features present
in the positives are kept. In layman terms, our moti-
vation is to generate artificial negatives that look like
the positives without being positives so that the dis-
criminating dimensions that are chosen stress the real
essence of the positives.
In fact, for the ANG based technique proposed
in (Hempstalk et al., 2008) it is shown that an ideal
solution is to generate negatives by sampling from
the very same distribution of the positives. Paramet-
ric models fitted to the positives (e.g., a Multivariate
Gaussian) could be a useful ANG. However, in high-
dimensional spaces fitting a parametric model seems
futile. Therefore we turn our attention towards non-
parametric and geometrically motivated ANG tech-
niques. The following are four simple methods for
generating artificial negatives:
Uniform. Negatives coming from the uniform distri-
bution are commonly used in the literature. As indi-
cated previously, the rationale for sampling the nega-
tives from the uniform is that of low-density rejection.
This method can perform poorly when the distribu-
tion of the actual negatives is far from uniform while
still having a big overlap with P (Scott and Blanchard,
2009), and it has important computational problems
when trying to cover high dimensional spaces.
Marginal. Generating negatives by random sam-
pling from the empirical marginal distribution of the
positives, that is, to randomly permute the values
within each feature, breaks the correlation between
the features while maintaining the artificial negatives
in dense areas of positives (Francois et al., 2007).
Breiman and Cutler, in their random forest implemen-
ARTIFICIAL DATA GENERATION FOR ONE-CLASS CLASSIFICATION - A Case Study of Dimensionality Reduction
for Text and Biological Data
205

tation (Breiman, 2001), apply this method to allow
the construction of forests which, as a byproduct, pro-
duce an emergent measure of proximities between ex-
amples and a ranking of features (Shi and Horvath,
2006).
Left-right. This method simple translates each ex-
ample in one of two directions, “left” or “right”. The
translation in each dimension depends on the ob-
served range of that dimension and is scaled by a
parameter ρ ∈ R, chosen a priori. Formally a
(i)
=
p
(i)
+ ρ
(i)
r, where r = (r
1
, r
2
, . . . , r
m
) is the vector of
features ranges (r
k
= |max(x
i
) − min(x
i
)|)and ρ
(i)
is
selected at random from −ρ (“to the left”) and ρ (“to
the right ”). See figure 2.
x
y
z
ρ = 1
y
z
x
ρ = 8
Figure 2: From the many directions possible, the LeftRight
generator displaces each positive point to the left (translate
each coordinate by a negative amount) or to the right (trans-
late each coordinate by a positive amount). By choosing to
translate in these two unique directions, we are generating
two clouds of points that are arbitrarily far from the original
sample of positives. Translation is an affine transformation
and so all the distances ratios get preserved in each of the
two clouds, so each cloud accounts for a different stochas-
tic view of the neighborhoods present in the positives. This
gives different related goals for LPP and also forces it to
“collapse” the positives, as the graph W is made up of at
least three connected components that arise from analogous
clouds of points in the original Euclidean space. Our arbi-
trary choice to scale up the translation by the range in each
dimension makes the distances between clouds larger in di-
mensions with high variance, in this case z.
Normalizer. This another simple transformation is
based on normalization. It projects the positives onto
the surface of the unit-L1 “sphere” to produce the
negatives (a
(i)
= kx
(i)
k
−1
1
x
(i)
) and then projects them
again onto the surface of the unit-L2 sphere (p
(i)
=
kx
(i)
k
−1
2
x
(i)
) to produce the normalized positives. See
figure 3.
4 RESULTS
In this section we study the behaviour of LPP applied
over samples of positives enriched with the negatives
Figure 3: Effect of the normalizer generator in two and
three dimensions. The normalizer ANG maps the posi-
tives (black) onto the unit-L1-sphere to produce the artifi-
cial negatives (internal simplex, green) and then maps them
again into the unit-L2-sphere (external circle, blue) to gen-
erate the normalized positives. This transformation keeps
in-class neighborhood relations and feature correlations be-
tween the two samples. It also generates two close clouds
of points, as it is easy to show that the Euclidean distance
between p
(i)
and a
(i)
is bounded by 1 and likely to be close
to 1. In high dimensions this usually generates interesting
contrasting distributions where the negatives are closer to
negatives and the positives are also closer to the negatives
than to other positives. It is difficult to illustrate this last ef-
fect in two or three dimensions, but it happens consistently,
for example, in the experiments described in section 4.
generated in the four ways explained in the previous
section. We do so over a suite of datasets, for which
it is known that dimensionality reduction is possible
and desirable, in two domains: text classification and
functional genomics.
4.1 Experimental Setup
In order to avoid complex experimental setups, we
will consider only reducing to one-dimension through
a linear transformation, represented by e. It is known
that this kind of dramatic dimensionality reduction is
possible for the text classification task (Kim et al.,
2005). In this way we avoid the problem of selecting
the optimal dimensionality and the threat of reporting
overoptimistic results due to multiple testing effects.
For the ANG we set the proportion π to 0.5, gener-
ating the same number of artificial negatives as train-
ing positives. For the left-right ρ parameter we use 20
that always generates well separated clouds of points.
As baseline for dimension reduction techniques we
apply the standard unsupervised LPP (using 5 as the
number of nearest neighbors), PCA and a Gaussian
random projection. Apart from those we also project
over the direction defined by the standard deviation
of each feature, that is, e = (σ
1
, σ
2
, . . . , σ
m
) where σ
k
is the standard deviation of feature k. The rationale
for this last technique, that we call StdDevPr, will be-
come clear when reading the experiments with text
classification. We also report the results got when ap-
plying OCC without dimensionality reduction. The
KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval
206

following are the two one-class classifiers we use:
Gaussian Model (Tax, 2001). Fit a unimodal mul-
tivariate normal distribution to the positives. When
applied to 1-dimensional data, this classifier simply
returns the distance to the mean.
One-class SVM. We use the one-class ν-SVM
(Sch
¨
olkopf et al., 2001) method, that computes hyper-
surfaces enclosing (most of) the positive data. We
set ν, the regularization parameter that controls how
much we expect our training data to be contaminated
with outliers, to 0.05. As it is common practice
in OCC we use the Gaussian kernel, initializing the
width of the kernel to the average pairwise Euclidean
distance in the training set.
In order to select an operating point for the classi-
fiers we compute a threshold by assuming that a 5%
of the training data are outliers. This is a common
choice in the one-class literature. The role of thresh-
old selection by train-rejection lies in one or both of
these two assumptions (a) the presence of noise and
some counterexamples in the train data, (b) our clas-
sifier is not powerful enough as to accommodate all
positive examples. Another underlying assumption is
that in the training data we have boundary cases, so
that the threshold will not be too tight as for reject-
ing too many positives. A more practical view is that,
probably, this is the most straightforward way of se-
lecting the operating point.
Threshold selection is directly related to the ro-
bustness and capital for one-class classifiers general-
ization capabilities. If it is too tight the number of
false negatives will be increased; this can happen if
the noise level specified by the user is too high. If it is
too loose, the number of false positives will increase;
this will happen if the noise level specified is too low.
In either case one-class classifiers become reject-all
or accept-all machines, which is a very common and
undesirable effect.
For each target class we perform a 10-fold cross-
validation, except for those classes with less than 10
examples, which we ignore, and those with sample
sizes between 10 and 15, for which we perform a
leave-one-out cross validation (in OCC this means
constructing a model using all positives to classify
all negatives, and constructing a model leaving out
each of the positives). Of course, the ANG sampling
and DR computations are also included in the cross-
validation loop, only granting them access to the train
data in each fold. We report the area under the ROC
curve (AUC) and the Balanced Accuracy Rate (BAR)
defined as the average of the True Positive (sensitiv-
ity) and True Negative (specificity) Rates.
4.2 Text Classification
We use a suite of text classification problems provided
by Forman (Forman, 2003)
1
. Those come from sev-
eral well-known text classification corpora (ohsumed,
reuters, trec...). In total this accounts for 265 different
classification tasks. These are high dimensional (from
2000 to 26832 features) low sample size datasets,
therefore the data is sparse. We use the Bag-of-Words
(BoW) representation that embodies a simplistic as-
sumption of word independence, and normalize each
document to unit-L2 norm, as is usual practice in in-
formation retrieval.
There is a fundamental trap when working with di-
mensionality reduction for text classification in OCC.
Due to the sparsity, many of the words do not appear
at all in any of the documents of the class. These
words are unobserved features, features that are con-
stant zero in the training set of a class. Unobserved
features are highly discriminative, but cannot be used
in a principled way for training one-class classifiers.
This phenomenon is pervasive, with unobserved ra-
tios per class ranging between 5% and 95% of the fea-
tures in the datasets evaluated. Unobserved features
can make a big difference in performance. For ex-
ample, using the Gaussian classifier the average AUC
varies from 0.9 when allowing unobserved features
in the training set to 0.68 when using only observed
features. In the present experiments we only use ob-
served features.
The results are shown in figure 4. The baseline
AUC for no dimension reduction is a poor 0.68. Nei-
ther PCA nor LPP provide useful projections when
trained with positive examples only. They are even
harmful performing worse than random projection,
which also performs poorly in this evaluation. In the
ANG realm we realize that both the Uniform and the
Marginal, while still improving over the baseline of
LPP, does not provide the best performance. There-
fore we focus on the three best techniques: Normal-
izer and LeftRight + LPP and the StdDevPr.
The StdDevPr is the best technique in our
test-bench. Its computation is extremely efficient
(O(mn)), requiring only a single pass over the pos-
itive examples. To the best of our knowledge it is
novel and have not been used before, although related
biases can be found in the literature (e.g., the term fre-
quency variance, where in a feature selection context
each word is scored by its variance in the whole cor-
1
Available for download at http://jmlr.csail.mit.edu/
papers/v3/forman03a.html. We used an extra data-
set, new3s, also supplied by Forman and available
at http://prdownloads.sourceforge.net/weka/19MclassText-
Wc.zip?download
ARTIFICIAL DATA GENERATION FOR ONE-CLASS CLASSIFICATION - A Case Study of Dimensionality Reduction
for Text and Biological Data
207

90.0
100.0
Gauss
60.0
70.0
80.0
x
100)
ocSVM
20.0
30.0
40.0
50.0
AUC(
x
0.0
10.0
Marginal Uniform Normalizer LeftRight LPP PCA RandomPr StdDevPr NoDR
SupervisedLPP+ANG NoANG
80 0
90.0
Gauss
60.0
70.0
80
.
0
0
0)
ocSVM
30.0
40.0
50.0
BAR(x1
0
0.0
10.0
20.0
Marginal Uniform Normalizer LeftRight LPP PCA RandomPr StdDevPr NoDR
SupervisedLPP+ANG NoANG
Figure 4: Cross-validation AUCs (top) and BARs (bottom)
averaged over 265 datasets/ classes in text classification.
pus of positives and negatives (Dhillon et al., 2003)).
It accounts for a very simple rationale: a dimension
(word) is promoted inside a class when it is used a
lot in several of the training documents (modelling
phenomena such as word burstiness (Madsen et al.,
2005)), always in relation to the size of these doc-
uments (recall that we work with normalized docu-
ments).
We came to consider using StdDevPr almost by
accident and only after carefully analyzing the ac-
tual reasons behind the success of LeftRight and the
Normalizer ANGs. We realized that the embeddings
found by LPP using these two ANG techniques where
highly correlated, so it became obvious that LPP was
responding to the same characteristic of our positives
in both cases. It was obvious too that because of the
range-based scaling on the translation part of the Left-
Right ANG, we were artificially stretching dimen-
sions with high variance. These embeddings are also
highly correlated with those found by StdDevPr, so
the the success when applying these ANGs techniques
is mainly attributed to their similarity to the StdDevPr
technique.
In the bottom part of Figure 4 the performance
of the simple threshold selection technique used is
shown. It is clear that only the StdDevPr enhanced
AUC is well used while both the ranking enhance-
ments provided by LeftRight and Normalizer, in spite
of having the same potential, are lost because of a
poor threshold selection strategy. The target dimen-
sionality (the dimensionality of the data after the ap-
plication of the DR technique) can be regarded as
a regularization parameter (Mosci et al., 2007). In
classification, when fixing the thresholding policy, it
controls the trade-off between sensitivity and speci-
ficity; overfitting and underfitting can be easily pro-
voked by a wrong selection of the target dimension-
ality. Studying the interactions between the threshold
and target dimension selection and the DR and clas-
sification techniques is essential, but lies beyond the
aims of this paper.
4.3 Translation Initiation Site
Prediction
We applied the same experimental setup to an impor-
tant biological problem: recognizing translation initi-
ation sites (TIS) in a genomic sequence. We used the
dataset described in (Liu and Wong, 2003)
2
. It has
3312 positive examples and 10063 negatives. These
examples have 927 features that represent counts (rep-
etitions) of k-grams in the DNA sequence. In this
case we do not normalize to unit-L2 norm, but instead
normalize each feature to be in [0, 1] in our training
set. Therefore this time the LeftRight ANG will not
promote high variance directions using the range as a
proxy, since all ranges are the same.
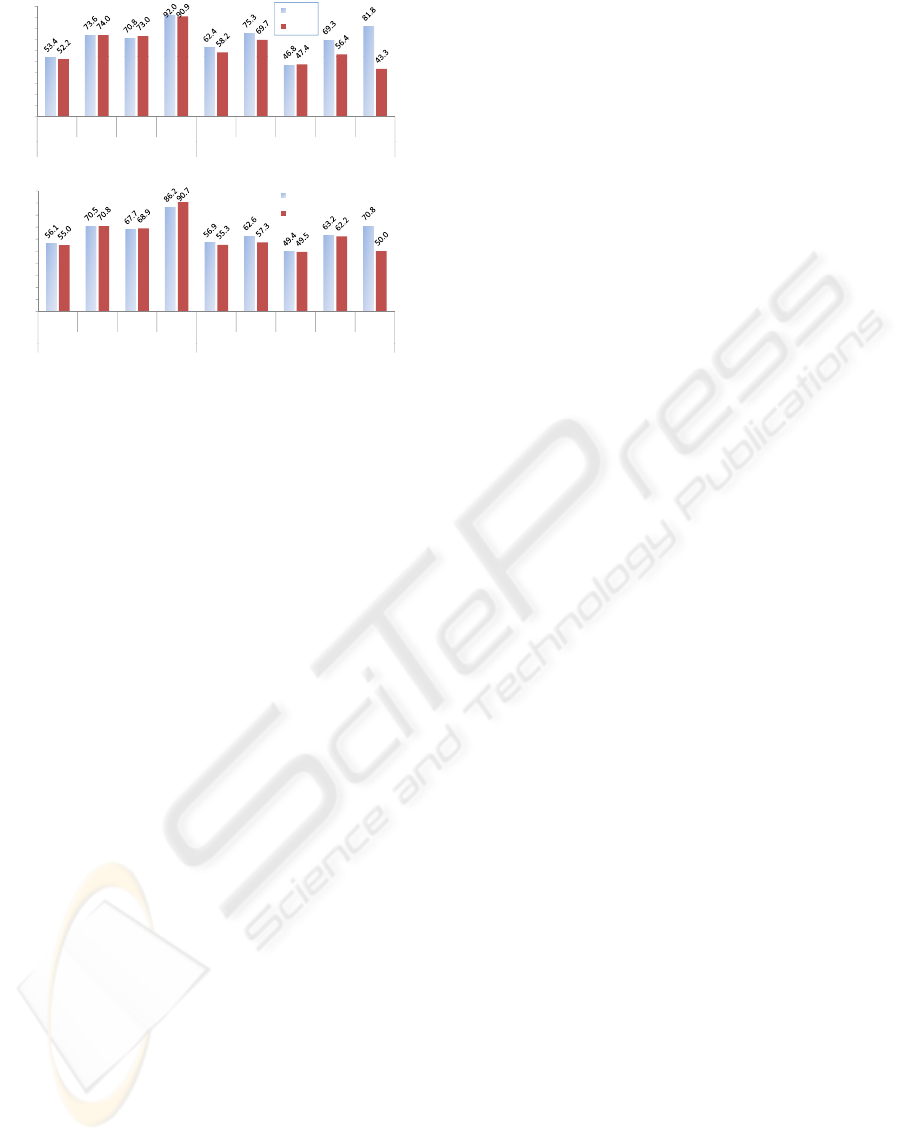
The results are shown in figure 5. In these results
we see two dominant techniques: using the original
feature set (AUC = 0.82) and the LeftRight + LPP
(AUC=0.92). That accounts for an increase of a 10%
by reducing the dimensionality to 1. Surprisingly,as
shown in the bottom part of the figure, by using our
simple thresholding technique we get classification
accuracies that are competitive with most of the re-
sults in the literature got by using supervised tech-
niques (Liu and Wong, 2003).
We still don’t have conclusive answers for why
LeftRight works so well in this case. Our hypothe-
sis is that our motivation when we designed the sim-
ple LeftRight ANG to collaborate with LPP in order
to “collapse the class” works. Referring to the dis-
tances of the embedded points, LPP does a good job
on getting them very close to zero in the training sets,
and getting similar effects in the test sets. The Uni-
form generator has an analogous effect on the training
sets but the embeddings are not so good at test time
(as reflected by its performance in figure 4), which is
probably due to LPP responding to specific stochastic
interactions in the artificial uniform sample.
5 CONCLUSIONS
We have explored the feasibility of artificial negative
generation techniques in the context of dimensional-
2
Available for download at http://datam.i2r.a-
star.edu.sg/datasets/krbd/SequenceData/TIS.html
KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval
208
100.0
Gauss
60.0
70.0
80.0
90.0
1
00)
ocSVM
20.0
30.0
40.0
50.0
AUC(x
1
0.0
10.0
Marginal Uniform Normalizer LeftRight LPP PCA RandomPr StdDevPr NoDR
SupervisedLPP+ANG NoANG
100.0
Gauss
70.0
80.0
90.0
)
Gauss
ocSVM
40.0
50.0
60.0
B
AR(x100
)
10.0
20.0
30.0
B
0.0
Marginal Uniform Normalizer LeftRight LPP PCA RandomPr StdDevPr NoDR
SidLPP ANG
N ANG
S
uperv
i
se
d
LPP
+
ANG
N
o
ANG
Figure 5: Cross-validation AUCs (top) and BARs (bottom)
for the TIS dataset.
ity reduction for one-class classification. Applying
very simple artificial negative generation techniques
working together with a locality preserving dimen-
sion reduction has shown promising results in a ex-
periment with a comprehensive set of text classifica-
tion datasets and a genomics dataset. This area of re-
search is by its very nature speculative, as ultimately
one always needs to rely on the relations between the
artificial sample and the actual negatives, the latter be-
ing unknown. It is also the case that for each ANG
mechanism we can find the corresponding unsuper-
vised bias. In the case of text classification we found
via this indirect approach that stretching up the di-
rections - words - which account for more variance
within the class once the documents are normalized
is a fast, reliable and class-dependent bias for dimen-
sion reduction in one-class classification. For the ge-
nomics dataset one of our proposed techniques excels
at finding discriminative representations and all seems
to indicate that this is due to our algorithm-design ra-
tionale working as expected.
This work can be extended by studying synergies
between ANG and corresponding supervised tech-
niques. For example, for text classification, apply-
ing Linear Discriminant Analysis together with para-
metric ANG techniques has shown consistent good
performance. We are also exploring the potential to
incorporate the other bit of information we have in
OCC, the testing point, to guide the creation of our ar-
tificial negatives. Artificial negatives could also lead
to data-driven techniques for other tasks in the clas-
sification system, like the threshold or target dimen-
sionality selections.
REFERENCES
Abe, N., Zadrozny, B., and Langford, J. (2006). Outlier
detection by active learning. In KDD: International
Conference on Knowledge Discovery and Data Min-
ing, pages 767–772.
Breiman, L. (2001). Random forests. Machine Learning,
45(1):5–32.
Chapelle, O., Sch
¨
olkopf, B., and Zien, A., editors (2006).
Semi-Supervised Learning. The MIT Press, Cam-
bridge, MA.
Chung, F. R. K. (1997). Spectral Graph Theory (CBMS
Regional Conference Series in Mathematics, No. 92).
American Mathematical Society.
Dhillon, I., Kogan, J., and Nicholas, C. (2003). Feature se-
lection and document clustering. In A Comprehensive
Survey of Text Mining, pages 73–100. Springer.
El-Yaniv, R. and Nisenson, M. (2006). Optimal single-class
classification strategies. In NIPS: Advances in Neural
Information Processing Systems.
Fan, W., Miller, M., Stolfo, S., Lee, W., and Chan, P.
(2004). Using artificial anomalies to detect unknown
and known network intrusions. Knowledge and Infor-
mation Systems, 6(5):507–527.
Forman, G. (2003). An extensive empirical study of fea-
ture selection metrics for text classification. Journal
of Machine Learning Research, 3:1289–1305.
Franc¸ois, D. (2008). High-dimensional Data Analysis:
From Optimal Metrics to Feature Selection. VDM
Verlag.
Francois, D., Wertz, V., and Verleysen, M. (2007). The
concentration of fractional distances. IEEE Trans. on
Knowl. and Data Eng., 19(7):873–886.
Hastie, T., Tibshirani, R., and Friedman, J. H. (2001). The
Elements of Statistical Learning. Springer.
He, X. and Niyogi, P. (2003). Locality preserving projec-
tions. In NIPS: Advances in Neural Information Pro-
cessing Systems.
Hempstalk, K., Frank, E., and Witten, I. H. (2008). One-
class classification by combining density and class
probability estimation. In ECML: European Confer-
ence of Machine Learning.
Kim, H., Howland, P., and Park, H. (2005). Dimension re-
duction in text classification with support vector ma-
chines. Journal of Machine Learning Research, 6:37–
53.
Liu, H. and Wong, L. (2003). Data mining tools for biolog-
ical sequences. Journal of Bioinformatics and Com-
putational Biology, 1(1):139–167.
Madsen, R. E., Kauchak, D., and Elkan, C. (2005). Model-
ing word burstiness using the dirichlet distribution. In
ICML: International Conference on Machine Learn-
ing, pages 545–552.
Manevitz, L. M. and Yousef, M. (2001). One-class SVMs
for document classification. Journal of Machine
Learning Research, 2:139–154.
ARTIFICIAL DATA GENERATION FOR ONE-CLASS CLASSIFICATION - A Case Study of Dimensionality Reduction
for Text and Biological Data
209

Mosci, S., Rosasco, L., and Verri, A. (2007). Dimension-
ality reduction and generalization. In ICML: Interna-
tional Conference on Machine Learning, pages 657–
664.
Sch
¨
olkopf, B., Platt, J. C., Shawe-Taylor, J. C., Smola, A. J.,
and Williamson, R. C. (2001). Estimating the support
of a high-dimensional distribution. Neural Computa-
tion, 13(7):1443–1471.
Scott, C. and Blanchard, G. (2009). Novelty detection: Un-
labeled data definitely help. In AISTATS: Artificial In-
telligence and Statistics, JMLR: W&CP 5.
Scott, C. D. and Nowak, R. D. (2006). Learning minimum
volume sets. Journal of Machine Learning Research,
7:665–704.
Shi, T. and Horvath, S. (2006). Unsupervised learning with
random forest predictors. Journal of Computational
& Graphical Statistics, 15:118–138.
Steinwart, I., Hush, D., and Scovel, C. (2005). A classifi-
cation framework for anomaly detection. Journal of
Machine Learning Research, 6:211–232.
Tax, D. M. J. (2001). One-class classification. Concept
learning in the absence of counterexamples. PhD the-
sis, Delft University of Technology.
Tax, D. M. J. and Duin, R. P. W. (2002). Uniform object
generation for optimizing one-class classifiers. Jour-
nal of Machine Learning Research, 2:155–173.
Tax, D. M. J. and Muller, K.-R. (2003). Feature extrac-
tion for one-class classification. In ICANN/ICONIP:
Joint International Conference on Artificial Neural
Networks and Neural Information Processing.
Villalba, S. D. and Cunningham, P. (2007). An evaluation of
dimension reduction techniques for one-class classifi-
cation. Artificial Intelligence Review, 27(4):273–294.
KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval
210
