
FUZZY SET THEORY BASED STUDENT EVALUATION
Zsolt Csaba Johanyák
Institute of Information Technology, Kecskemét College, Izsáki út 10, Kecskemét, Hungary
Keywords: Fuzzy grading system, Student performance evaluation.
Abstract: The evaluation of students’ learning achievements contains in several cases a lot of decisions that are based
on the expertise and the opinion of the evaluator. Often this opinion is from nature vague and therefore this
field is a good application area for fuzzy set theory based supporting methods and software
implementations. In this paper, a new method called FUSBE (Fuzzy Set Theory Based Evaluation) is
presented. It supports the scoring and grading of the students allowing the evaluator to express his or her
judgment by the means of fuzzy sets that are later aggregated using fuzzy arithmetic. The method is
transparent and easy-to-implement.
1 INTRODUCTION
The evaluation of student’ assignments, homeworks,
software, narrative answers, etc. when a fully
automated scoring is not possible involves a lot of
decisions that are from nature subjective and
therefore usually the deviation between the marks or
grades given by different evaluators and on different
occasions for the same answers could be very high.
The subjectivity can be reduced in several cases
using standardized scoring criteria, specific
examples of responses to the questions, or even
sample software solutions but none of these
approaches can solve all the problems. Besides, the
more specific a guide is the more time consumable
its learning and its application is. Furthermore, it is
not always an applicable solution.
Another approach for dealing with subjectivism
arises from the fuzzy set theory. The application of
linguistic terms and related fuzzy sets is common to
the human thinking and can result in decreasing the
evaluation’s sensitivity to “noisy” scoring data. In
this case the relation between the linguistic terms
and the traditional marks is established by the means
of membership functions.
Starting from the early 1990s several ideas have
been developed in order to find a better evaluation
technique by the help of fuzzy techniques. Biswas
(1994) proposed a particular (FEM) and a
generalized (GFEM) method that were based on the
vector representation of fuzzy membership functions
and a special aggregation of the grades assigned to
each question of the student’s answerscripts. Chen
and Lee (1999) suggested a simple (CL) and a
generalized (CLG) method that produced
improvements by applying a finer resolution of the
scoring interval and by including the possibility of
weighting the four evaluation criteria. Nolan (1998)
introduced a fuzzy classification model for
supporting the grading of student writing samples in
order to speed up and made more consistent the
evaluation.
All the mentioned methods have their advantages
and disadvantages that will be discussed in details in
section 2 along with their short presentation. All of
the methods contain heuristic elements and therefore
there is always a possibility to develop new
techniques that could bring advantages from one or
more aspects.
In this paper, a new approach is suggested that
tries to induce improvements by reducing the
computational needs as well as by eliminating the
summarization of the potential errors caused by the
application of the similarity measure and quasi
defuzzification at the evaluation of each question.
The rest of this paper is organized as follows.
Section 2 contains the presentation and discussion of
some well known methods followed by the
introduction of the new technique in section 3.
53
Csaba Johanyák Z. (2009).
FUZZY SET THEORY BASED STUDENT EVALUATION.
In Proceedings of the International Joint Conference on Computational Intelligence, pages 53-58
DOI: 10.5220/0002312300530058
Copyright
c
SciTePress

2 FUZZY SET THEORY BASED
EVALUATION METHODS
This section presents a short review of the basic
ideas and key features of some student evaluation
methods that apply elements of fuzzy set theory in
order to facilitate the grading of the students’
academic performance.
2.1 FEM and GFEM
The key idea of the Fuzzy Evaluation Method
(FEM) (Biswas, 1994) is that each question in the
student answerscript is evaluated independently with
a discrete fuzzy set containing membership values
for six uniformly distributed predefined points (X) of
the traditional percentage based evaluation scale
[0,100].
{}
100,80,60,40,20,0=X
(1)
The resulting fuzzy set is compared to all of the
so called Standard Fuzzy Sets (SFSs). The SFSs are
defined on the same universe of discourse [0,100]
corresponding to the grading standard of the
university. Each SFS corresponds to a traditional
grade (e.g. Excellent). The comparison is made by
the means of a similarity degree that is calculated by
()
()
jjii
ji
j
ii
SFSSFSEE
SFSE
SFSES
⋅⋅
⋅
=
,max
,
,
(2)
where the index i denotes the ordinal number of
the question,
i
E is the vector containing the
membership values of the evaluation and
j
SFS is
the j
th
standard fuzzy set, and “.” denotes the dot
product. Further on, the degree corresponding to the
SFS with maximum similarity will represent the
evaluation of the actual question.
After processing all the questions a total score is
determined by calculating the weighted average of
the representative values (midpoints) of the fuzzy
sets corresponding to the individual grades assigned
to the questions by
() ()()
100
1
∑
=
⋅
=
n
i
ii
gPQT
TS
,
(3)
where
()
100
1
=
∑
=
n
i
i
QT ,
(4)
where the index i denotes the ordinal number of
the question, n is the total number of questions,
i
Q
is the question,
(
)
i
QT is the weight of the question,
i
g is the degree assigned to the question,
(
)
i
gP is
the representative value of the degree, and “.”
symbolizes the dot product.
The Generalized Fuzzy Evaluation Method
(GFEM) (Biswas, 1994) evaluates each answer from
four different points of view, namely the accuracy of
information, the adequate coverage, the conciseness,
and the clear expression. The arithmetic mean of the
midpoints of the fuzzy sets representing the four
grades assigned will represent the evaluation of the
given question expressed with marks between 0 and
100
()
4
4
1
∑
=
=
k
ik
i
gP
E
,
(5)
where k identifies the point of view. One
calculates the total score (TS) as a weighted average
of the individual marks
()()
100
1
∑
=
⋅
=
n
i
ii
EQT
TS
.
(6)
The applied weighting is the same as in the case
of FEM.
The advantage of FEM and GFEM is their easy-
to-understand and easy-to-implement character.
Their disadvantage is that they determine separate
grades for each question applying a rounding to the
most similar grade, which introduces an error in
each evaluation step. The error summarizes in
course of the evaluation of the answerscript and at
the end it can lead to a quite strange final result.
The use of the midpoints in the total score
calculation is a quasi defuzzification before the final
aggregation, which also can mislead the evaluation.
Besides, the relation between the SFSs and the
values of the midpoints is not defined clearly.
However, the SFS based concept can soften the
difference between the final scores given by
independent evaluators owing to the feature that
slightly differing evaluations can result in the same
grade.
2.2 CL and CLG
The CL method proposed by Chen and Lee (1999)
has several similar elements to FEM. However, they
use a slightly different terminology. The method
IJCCI 2009 - International Joint Conference on Computational Intelligence
54

defines a finer resolution of the scoring scale, which
is in this case the interval [0,1] by using eleven so
called satisfaction levels that are crisp similar to the
traditional grade based evaluation. Here one uses an
extended grade sheet for the evaluation’s
documentation, which contains for each question
eleven cells that have to be filled in by the evaluator
with values between 0 and 1. They describe in what
amount the answer given by the student belongs to
the predefined satisfaction levels. They can be
considered also as membership values. After filling
in the eleven cells of the current row a degree of
satisfaction
()
i
QD is calculated for the current
question
i
Q by
()
()
∑
∑
=
=
⋅
=
11
1
11
1
j
ij
j
jij
i
y
SLTy
QD
,
(7)
where
ij
y is the membership value assigned for
the j
th
satisfaction level
j
SL
, and
(
)
j
SLT
is the
upper bound of the score interval corresponding to
j
SL
.
Finally, the total score of the student is
calculated as a weighted average of the individual
degrees of satisfaction
()
∑
=
⋅=
n
i
ii
QDsTS
1
,
(8)
where the weights have to satisfy the equation
100
1
=
∑
=
n
i
i
s .
(9)
Chen and Lee also published in (Chen & Lee,
1999) a generalized version of their method (CLG).
The applied approach is similar to GFEM; it uses the
same four criteria for evaluation of each question
from different points of view. Thus one calculates
four degrees of satisfaction for each question. The
overall mark
()
i
QP of the response is calculated as
a weighted average of the four degrees of
satisfaction
()
()
∑
∑
=
=
⋅
=
4
1
4
1
,
k
k
k
ik
i
w
kQDw
QP
,
(10)
where
k
w is the weight of the k
th
criteria, and
(
)
kQD
i
, is the degree of satisfaction of the k
th
criteria. CLG determines the total score by
substituting
(
)
i
QP for
(
)
i
QD in (8).
The CL and CLG methods are in several ways
similar to the FEM-GFEM pair. They introduce
improvements by a finer resolution of the scoring
interval and by allowing the weighting of the four
criteria. These modifications increase the
computational need, however, this not a great
problem owing to the fact that the methods are
applicable in practice only when a software support
is ensured.
2.3 Evaluation Based on Fuzzy
Classification
Nolan (1998) reports the successful development,
implementation and application of a fuzzy rule based
model called Expert Fuzzy Classification System
(EFCS). EFCS was developed in order to support the
evaluation of fourth grade students’ writing samples
in case of narrative response exams. The system
supports a well defined rating process aiming the
reduction of the time needed for the evaluation as
well as making the results more consistent.
The underlying rule base was created using the
rules of the scoring guide applied in case of the
traditional way of evaluation. The antecedent parts
of the rules examine the existence of some skills like
character recognition, text understanding, etc., which
are represented by the input linguistic variables. The
rules infer the measure of skills like reading
comprehension, etc. that are represented by the
consequent linguistic variables. An example rule is
IF understanding is high
AND character-recognition is strong
THEN reading-comprehension is high.
The resolution of the scoring universe is not
high; the partitions usually consist of three fuzzy
sets. The membership functions were developed
based on the interval definitions given by a group of
expert teacher graders.
In course of the evaluation the rater assigns one
score for each dimension of the antecedent universe
of discourse (input linguistic variables) and the
system determines a final score using a Mamdani-
type (Mamdani & Assilian, 1975) inference
mechanism.
Although EFCS is an application specific system
its concept easily can be used for evaluation tasks
where there is available a clear defined rule system
FUZZY SET THEORY BASED STUDENT EVALUATION
55
(scoring guide) based on symbolic statements in the
antecedent and consequent parts of the rules.
The advantage of EFCS is that it achieved both
of the aims of its developer, namely the evaluation
time reduction and the increase of the consistence of
the grading given by different raters.
The drawback of EFCS is that it requires a
tedious preparation work. The original system
contained 200 rules and the participation of a group
of expert grader was necessary for the determination
of the fuzzy partitions.
3 FUZZY SET THEORY BASED
EVALUATION
This section reports the development of a fuzzy set
theory based evaluation model for student writing
exams. The first subsection will describe the
traditional approach applied in our institute. The
proposed fuzzy solution for this task and the
software based on it will be presented in the second
subsection.
3.1 The Traditional Approach
Although there is no standardized scoring guide in
our institute usually the rating of the assignments
with narrative responses happens as follows. The
total number of marks for an assignment or group of
consecutive assignments is 100. This number is
divided between the questions of the assignment(s).
Table 1: Relation between scores and grades.
Score intervals Grades
0 - 50
Unsatisfactory
51 - 60
Satisfactory
61 - 75
Average
76 - 85
Good
86 - 100
Excellent
Thus the lecturer that prepares the question sheet
assigns marks between 1 and 25 to each question,
viz. each sheet contains at least four questions.
Unlike the previously presented methods our
institute does not use explicit weight number set, the
significance of a question is expressed by the
number of marks a student can achieve in case of a
perfect response. The assignment of the actual
number of marks is based on the expertise of the
evaluator. At the end we calculate a total score
calculated by summarizing the individual scores
achieved in case of each question, and the final score
is mapped to a five-graded scale. The grades are
“unsatisfactory”, “satisfactory”, “average”, “good”,
and “excellent”. The mapping is standardized; the
score intervals corresponding to the grades are
presented in Table
1. They also can be described by
the crisp sets on Figure
1.
0
20
40
60
80
100
0
2
4
6
8
1
unsatisfactory
satisfactory average good excellent
0 51617686100
x
μ
1
Figure 1: Traditional grades represented as crisp fuzzy
sets.
3.2 Fuzzy Set Based Evaluation
In course of the development of the Fuzzy Set Based
Evaluation (FUSBE) method the following demands
were taken into consideration:
Although computational complexity may not be
an issue owing to the capabilities of the
nowadays available computers, the method
should be as simple as possible in order to be
understandable for both the students and the
evaluators; all participants of the evaluation
process have to consider it as a fair deal;
The method should enable for the evaluator to
express the vagueness in her or his opinion in
form of fuzzy sets in case of each question;
In case of one-valued scoring (singleton fuzzy
sets) the model should lead to the same result
as the traditional approach.
In order to fulfil the above mentioned
requirements the application of fuzzy arithmetic as
score aggregation tool and the use of Centre Of Area
(Kóczy & Tikk, 2000) defuzzification method has
been selected.
Thus the evaluation process is the following. In
case of each question the evaluator determines the
fuzzy score by the means of a fuzzy number.
Theoretically from the rating model’s point of view
the set of applicable membership function types is
not limited as far as they fulfil the CNF (convex and
normal fuzzy set) criteria. However, like any other
fuzzy approach based evaluation model FUSBE is
practically applicable only when the calculations are
IJCCI 2009 - International Joint Conference on Computational Intelligence
56
done by a computer. Therefore the cardinality of the
selectable membership function types becomes an
implementation detail.
For now the piece wise linear membership
functions that can be described by a trapezoid (i.e.
trapezoid, square, rectangle, triangle, and singleton)
are supported by our program. Other fuzzy set shape
types like piece wise linear forms with more than
four vertices and non-linear forms like bell shaped,
sigmoid, Π, L-R, etc. will be included in future
versions of the software.
The input of the fuzzy scores does not require
any typing. The graphical user interface (GUI) is so
designed that the parameters of the fuzzy sets can be
set by the help of controls using the mouse. We
consider only CNF sets as fuzzy scores of a
question. All of the parameters have default values;
the evaluation starts with a trapezoid situated at the
middle of the scoring interval. In case of the
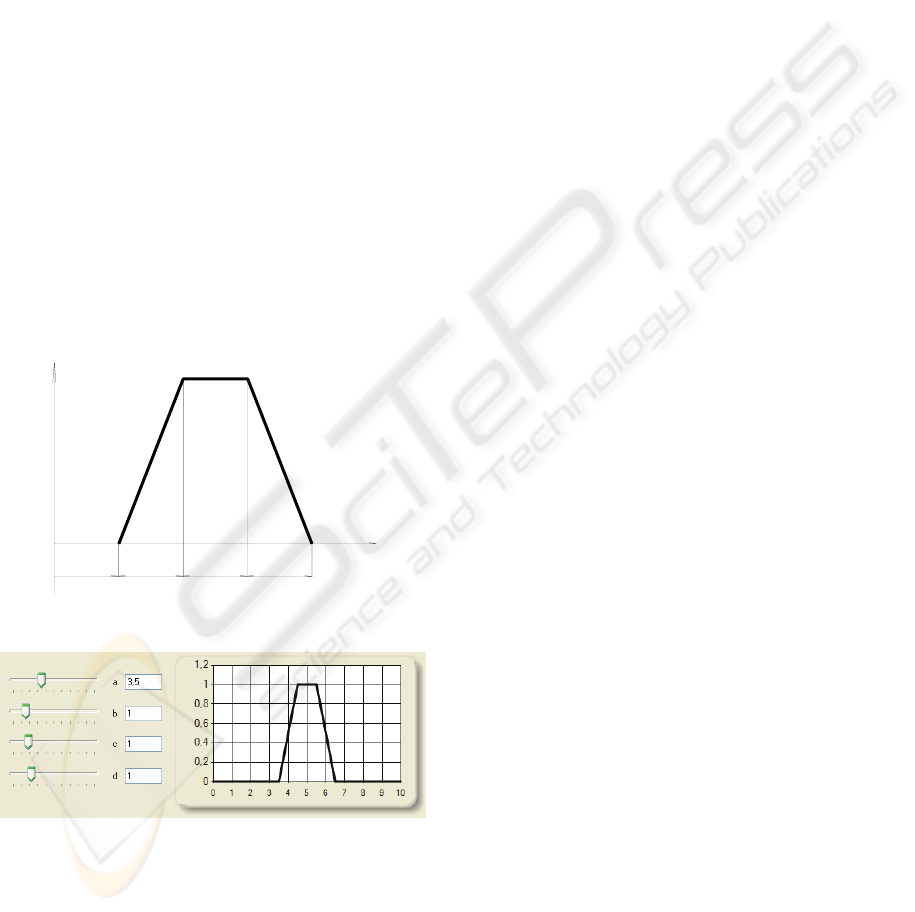
trapezoid shaped membership functions (Figure
2)
one needs to specify at most four parameters that
define the position (a) of the set and the three width
values (b, c, and d). One modifies the default
parameters with trackbars using the mouse (Figure
3).
b c da
x
μ
Figure 2: Parameters of a trapezoidal shaped fuzzy score.
Figure 3: Input of the fuzzy score.
The total fuzzy score is calculated as a sum of
the fuzzy scores given to the individual responses.
Conform to the theory of the fuzzy arithmetic it is
calculated α-cut wise, where an α-cut of a fuzzy set
is defined by
[
]
(
)(
]
{
}
1,0;| ∈≥∈=
ααμ
α
xXxA
A
.
(11)
Thus an α-cut of the total fuzzy score (
TFS )
will be
[] []
∑
=
=
n
i
i
FSTFS
1
α
α
,
(12)
where
n is the number of questions and
i
FS is
the fuzzy score of the
i
th
question. The calculations
are done by the help of the lower and upper
endpoints of the
α-cut
[
][]
{}
{
[]
{}}
,sup
,inf|
α
αα
TFSx
TFSxXxTFS
≤
≥∈=
(13)
where
[]
{}
[]
{}
α
α
i
n
i
FSTFS
∑
=
=
1
infinf ,
(14)
[]
{}
[]
{}
α
α
i
n
i
FSTFS
∑
=
=
1
supsup .
(15)
In the general case the resulting fuzzy set
determined as a union of its α-cuts by
[]
U
1
0+=
=
α
α
TFSTFS
(16)
requires a high number of α-cuts depending on
the demanded accuracy of the result. However, in
case of trapezoidal shaped membership functions
one can simplify the calculations by using the two
relevant
{
}
1,0
+
α levels.
Owing to the fact that we have been bound to the
total score – grades mapping presented in section 3.1
one has to defuzzify the TFS. FUSBE uses Center
Of Area (Kóczy & Tikk, 2000) type defuzzification
for this task. Thus the method fulfils all the demands
set at the beginning of the section.
4 CONCLUSIONS
The evaluation of the students’ performance in cases
when the process cannot be fully automated contains
and will always contain subjective elements that can
lead to different scorings depending on the
evaluator, on the time of the evaluation, and on other
known or unknown factors.
FUZZY SET THEORY BASED STUDENT EVALUATION
57

Recently several computational intelligence
based methods have been published in order to deal
with this subjectivism or to reduce its negative
effects. Three of them are presented and examined
shortly in the first part of the paper. The second part
of the paper introduces a new approach that also
possesses a software support.
The method FUSBE is simple, easy-to-
understand, and fulfils the conditions demanded on
this kind of evaluation approaches. Conform our
experience it is accepted by both concerned parties
the students and the teachers.
Further research plans cover the development
and implementation of a student evaluation method
based on fuzzy inference (Kovács, 2006)(Hladek et
al., 2008) including the automatic fuzzy model
identification (Botzheim et al., 2001)(Gál & Kóczy,
2008) (Precup et al., 2008) as well.
ACKNOWLEDGEMENTS
This research was supported by the National
Scientific Research Fund Grant OTKA K77809 and
the Kecskemét College, GAMF Faculty Grant
1KU16.
REFERENCES
Biswas, R. (1995). An application of fuzzy sets in
students’ evaluation. Fuzzy Sets and System, 74(2),
187–194.
Botzheim, J., Hámori, B., & Kóczy, L.T. (2001).
Extracting trapezoidal membership functions of a
fuzzy rule system by bacterial algorithm, 7th Fuzzy
Days, Dortmund 2001, Springer-Verlag, 218-227.
Chen, S. M., & Lee, C. H. (1999). New methods for
students’ evaluating using fuzzy sets. Fuzzy Sets and
Systems, 104(2), 209–218.
Gál, L., & Kóczy, L.T. (2008). Advanced Bacterial
Memetic Algorithms, Acta Technica Jaurinensis,
Series Intelligentia Computatorica, Vol. 1. No. 3.,
225-243.
Hládek, D., Vaščák, J., & Sinčák, P. (2008). Hierarchical
fuzzy inference system for robotic pursuit evasion
task, in Proc. of the 6th International Symposium on
Applied Machine Intelligence and Informatics (SAMI
2008), January 21-22, Herľany, Slovakia, 273-277.
Kóczy, L. T. & Tikk, D. (2000). Fuzzy rendszerek,
Typotex Kft., Budapest.
Kovács, Sz. (2006). Extending the Fuzzy Rule
Interpolation "FIVE" by Fuzzy Observation, Advances
in Soft Computing, Computational Intelligence,
Theory and Applications, Bernd Reusch (Ed.), S
pringer Germany, 485-497.
Mamdani, E. H. & Assilian, S. (1975). An experiment in
linguistic synthesis with a fuzzy logic controller.
International Journal of Man Machine Studies, Vol. 7,
1-13.
Nolan, J. R. (1998). An expert fuzzy classification system
for supporting the grading of student writing samples.
Expert Systems With Applications, 15, 59-68.
Precup, R.E., Preitl S., Tar, J. K. , Tomescu, M. L.,
Takács, M., Korondi, P. Baranyi, P. (2008). Fuzzy
control system performance enhancement by Iterative
Learning Control. IEEE Transactions on Industrial
Electronics, vol. 55, no. 9, 3461-3475.
IJCCI 2009 - International Joint Conference on Computational Intelligence
58
