EVOLUTION STRATEGIES COMPARED TO GENETIC

ALGORITHMS IN FINDING OPTIMAL SIGNAL TIMING

FOR OVERSATURATED TRANSPORTATION NETWORK

Ali Hajbabaie and Rahim F. Benekohal

Civil and Environmental Engineering, University of Illinois at Urbana Champaign

205 N Mathew ave, Urbana, Illinois, U.S.A.

Keywords: Traffic Signal Optimization, Oversaturated Network, Evolution Strategies, Genetic Algorithms.

Abstract: This paper compares the performance of Evolution Strategies (ES) with simple Genetic Algorithms (GAs)

in finding optimal or near optimal signal timing in a small network of oversaturated intersections with

turning movements. The challenge is to find the green times and the offsets in all intersections so that total

vehicle-mile of the network is maximized. By incorporating ES or GA with the micro-simulation package,

CORSIM, we have been able to find the near optimal signal timing for the above-mentioned network. The

results of this study showed that both algorithms were able to find the near optimal signal timing in the

network. For all populations tested in this study, GA yielded higher fitness values than ES. GA with a

population size of 300, and selection pressure of 10% produced the highest fitness values. In GA for

medium and large size populations, a lower selection pressure produced better results while for small size

population a large selection pressure resulted in better fitness values. In ES for small size population, larger

µ/λ yielded better results, for medium size population both µ/λ ratios produced similar results, and for large

size population smaller µ/λ provided better results.

1 INTRODUCTION

Traffic congestion in major US metropolitan areas

costs $87 billion dollars annually. These costs plus

other negative effects of traffic congestion, calls for

practical methods for managing congestion in

transportation networks. Transportation supply

management can effectively reduce congestion in a

network by determining the optimal signal timing

that provides maximum capacity. In this study, two

different methods, ES and GAs, were used to find

the optimal or near optimal signal timing for a

transportation network consisting of nine

oversaturated intersections with turning movements.

In the past 10 years, much research has been

conducted to optimize signal timing in transportation

networks. A few examples are: Abu-Lebdeh and

Benekohal (2000) considered a two-way arterial

consisting of several intersections and tried to

manage the queues on this oversaturated arterial

using Gas. Chang and Sun (2003) considered a

network of 12 oversaturated and 13 undersaturated

intersections and proposed the Maximal Progression

Possibility method to minimize the delay and total

number of stops in the network by choosing the most

critical intersection and removing congestion from

that. Girianna and Benekohal (2004) considered an

oversaturated network consisting of 20 intersections

with one-way streets and used GAs to solve the

problem. Their algorithm was able to determine a

common cycle for the network and coordinate the

signals to remove congestion from the network.

Sanchez Medina et al. (2008) used GA to determine

optimal signal timing in two urban areas in Spain

and in one of their case studies increased the fitness

by 10% compared to the currently used signal

timing.

Similar to GAs, Evolution Strategies (ES) are

meta-heuristic approaches that start with a

population of candidate answers and try to improve

the fitness of the population over generations. Beyer

and Schwefel (2002) explained different aspects of

ES in their comprehensive introduction to ESs. ES

have been used extensively as an optimization

engine in a variety of scientific fields; however, we

did not find any study using ES to optimize signal

timing in transportation networks. This motivated us

to compare ES with GAs in finding signal

optimization solutions.

298

Hajbabaie A. and Benekohal R. (2009).

EVOLUTION STRATEGIES COMPARED TO GENETIC ALGORITHMS IN FINDING OPTIMAL SIGNAL TIMING FOR OVERSATURATED TRANS-

PORTATION NETWORK.

In Proceedings of the International Joint Conference on Computational Intelligence, pages 296-301

DOI: 10.5220/0002316202960301

 SciTePress

In this study, ES and GAs were used to find the

optimal or near optimal signal timing for a small size

oversaturated transportation network. Different

settings of GAs have been used and compared to

different settings of ES and their benefits and

drawbacks are discussed. The next sections discuss

methodology, results and our conclusions.

2 METHODOLOGY

In this section, the problem statement and

formulation, and the methodology to solve the

problem are presented.

2.1 Signal Optimization Problem

In signal optimization the goal is to find signal

timing such that a measure of effectiveness is

optimized. In this study, we are trying to maximize

total vehicle-mile in the network. The network is

oversaturated meaning that the traffic demand in the

network is more than the capacity. By signal timing,

we mean green times for each movement at the

intersection and the offsets. To study if ES and GAs

are capable of solving the signal optimization

problem, a simulated oversaturated transportation

network is used. This symmetric network consists of

nine intersections forming a rectangular grid as

shown in Figure 1. The length of each street is 2000

ft (including the entry and exit links as well).



Entry

Point

Figure 1: The schematic study network.

Traffic consists of only passenger cars; and they

enter the system at nine entry points shown in Figure

1. At each entry point, the volume is 1000 passenger

cars per hour per lane. It is assumed that 70% of

vehicles go straight, 10% turn right, and the

remaining 20% turn left. A fixed time signal timing

plan is used. All streets are two-way with one

approach lane per direction. At each intersection a

1000 ft long left turn pocket is assumed to avoid the

through lane being blocked by the left turning

vehicles. The traffic signal is assumed to have 4

phases, staring with left turn green arrows and

continued by through traffic green for each

direction.

ES or GAs determines the green times

(consequently the cycle lengths) and the offset for

each intersection to improve the total vehicle-mile

travelled in the entire network.

2.2 Signal Optimization Problem

Formulation

The problem could be formulated as an optimization

problem where we try to maximize total vehicle-

mile in the network. Vehicle-mile depends on the

signal timing of each intersection. In this problem,

the vehicles are moved in the network by CORSIM

simulation model and the vehicle-mile travelled is

tallied by software as well. We assumed that the left

turn green times are between 7 and 15 seconds. A

minimum of 20 seconds and a maximum of 80

seconds of green time are assumed for the through

traffic. The signal optimization problem is

formulated as follows:

(

,Of

)

s.t.

7 ≤ g

≤15

20 ≤ g

, g

≤ 80

0 ≤ Off

≤ C

= g

+ g

4 i

+14

1..9

Where:

),(

iki

Offgf

: is the total vehicle-mile in the

network, i: is the intersection index, g

: are the

left turn green times at intersection i, g

: are the

through traffic green times at intersection i, Off

: is

the offset at intersection i, C

: is the cycle length at

intersection i, and number 14: is the lost time at each

intersection.

2.3 How the Problem is Solved

For signal timing problem, each individual consists

of signal timing for the whole network, and the

fitness function is the total vehicle-mile travelled in

the entire network. The ES Algorithm used in this

study uses three different recombination methods

which are: global intermediary, local intermediary,

and discrete recombination. Each time one of these

recombination operators is chosen randomly with

similar probabilities. In addition, a correlated

mutation is used. For simple GA that is used,

tournament selection with replacement, two-point

crossover with probability of 0.85, and simple

mutation with probability of 0.01 are used.

To solve the problem with ES, the initial

population is randomly generated and the fitness of

all individuals is evaluated (by CORSIM). Using

recombination and mutation, the descendants are

generated and their fitness is evaluated by CORSIM.

Using selection operator, the parents for the next

EVOLUTION STRATEGIES COMPARED TO GENETIC ALGORITHMS IN FINDING OPTIMAL SIGNAL TIMING

FOR OVERSATURATED TRANSPORTATION NETWORK

299

generation are selected and this process is continued

until the termination criteria are met.

To solve the problem by GAs, the initial

population is randomly generated and the fitness of

all individuals is evaluated (by CORSIM). Then

using selection operator, the mating pool is formed

and the individuals are crossed over and mutated to

form the next generation. The fitness of all

individuals in the new generation is evaluated by

CORSIM and this procedure is continued until the

termination criteria are met.

The problem is solved using a PC with Pentium

4 CPU with clock time of 3.2 GHz, and memory of 1

GB. Each run of the algorithm that contains 9000

times fitness function evaluations takes around 8

hours of CPU time. For each setting, three different

seeds are used: 12345701, 52345681, and 92345723

(unique numbers). For each seed, the fitness of each

generation is the maximum fitness of the population

in that generation and the average of these three

fitness values is the reported fitness value.

3 RESULTS

We made both ES and GAs algorithms to evaluate

the objective function 9000 times in order to get

comparable results. In the following sections, details

on fine tuning GA and ES will be presented and then

the two methods will be compared.

3.1 Fine Tuning GA

In order to get good results from GAs, GA

parameters were selected according to Goldberg et

al. (1993). Three different population sizes were

tested: 25, 75, and 300 corresponding to a small,

medium size, and large population respectively. For

all of these three population sizes, tournament

selection with replacement with two different

pressures was tested: 40%, and 10%. These selection

pressures correspond to a high and a low selection

pressure. The values of fitness function versus the

number of fitness function evaluations are presented

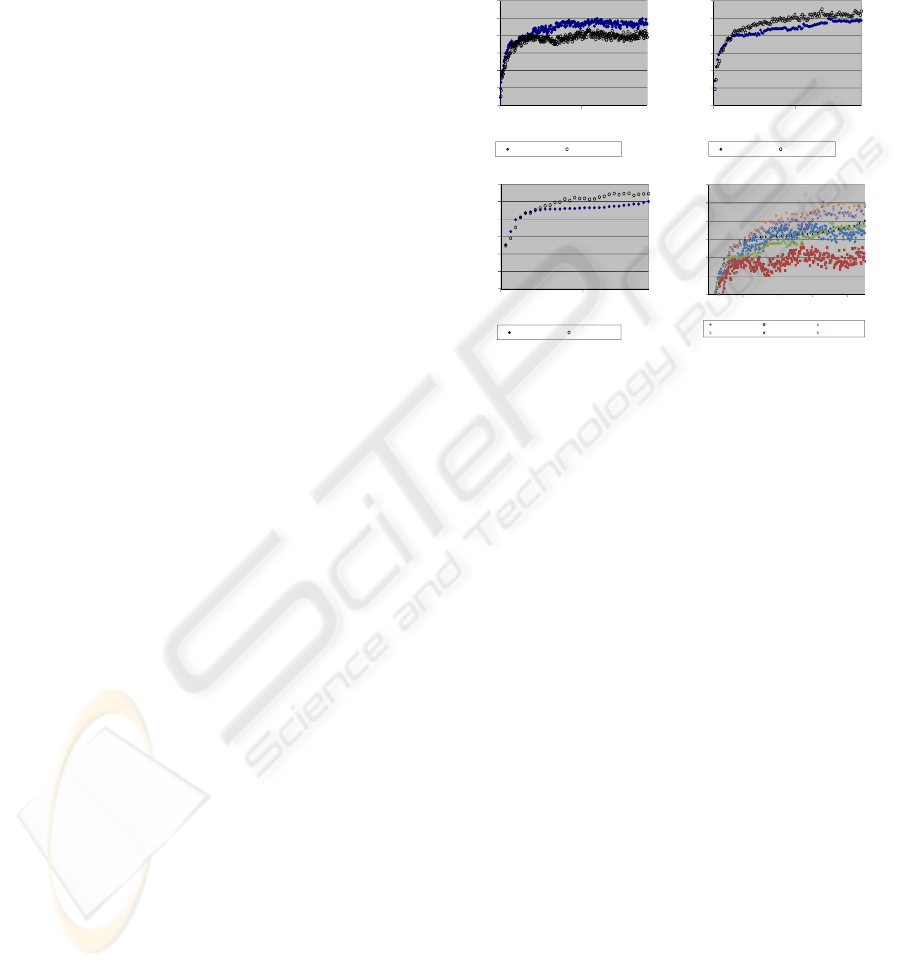
in Figure 2 separately for each population size.

For medium and large size populations (75

and 300 in case study), using a low selection

pressure results in better fitness values. The reason is

that a large selection pressure ends up selecting the

best individuals over and over and does not let other

individuals (that are less fit) to participate in

generating the next population. The less fit

individuals my pass some good genes and end up

creating a descendant with a higher fitness value. In

an extreme case, choosing a selection pressure of

100% forces the algorithm to choose the fittest

individual of the population each time. This setting

does not provide any good result and will be trapped

in a local optimum. On the other hand, a very small

selection pressure results in choosing parents almost

randomly. This way of choosing parents does not

pass the good genes to the next generation and does

not result in a significant increase in fitness value.

3500

3600

3700

3800

3900

4000

4100

0 5000

Fitness Value

No of Fitness Function Evaluations

SP = 40% SP = 10%

3500

3600

3700

3800

3900

4000

4100

0 5000

Fitness Value

No of Fitness Function Evaluations

SP = 40% SP = 10%

a) Population size = 25 b) Population size = 75

3500

3600

3700

3800

3900

4000

4100

0 5000

Fitness Value

No of Fitness Function Evaluations

SP = 40% SP =10%

3800

3850

3900

3950

4000

4050

4100

0 2000 4000 6000 8000

GA 25-40% GA 25-10% GA 75-40%

GA 75-10% GA 300-40% GA 300-10%

NoofFitnessFunctionEvaluations

FtinessValue

c) Population size = 300 d) All settings

Figure 2: Effects of SP on the value of fitness function for

different population sizes (*SP: Selection Pressure).

On the other hand, for a small population size, a

higher selection pressure should be used. The reason

is that when the population size is small (25 in this

case) a relatively small selection pressure (10%)

results in selecting only two individuals each time;

and then selecting the fittest of the two as one of the

parents. Figure 2 supports the above-mentioned

statements. When the population size is equal to 25,

setting selection pressure equal to 40% results in

better fitness values compared to setting selection

pressure equal to 10%. However, when the

population size becomes 75 or 300, choosing a

smaller selection pressure results in better fitness

values. Based on Figure 2, GA setting that provided

numerically better fitness values is GA 300-10%.

This setting has been chosen as the best setting in

GA.

3.2 Fine Tuning ES

Six different settings were tested to fine tune ES.

These settings were chosen corresponding to the

setting used for GA. These six settings are: ES10,25,

ES4,25, ES30,75, ES7,75, ES120,300, and

ES20,300 and correspond to GA25-40%, GA25-

10%, GA75-40%, GA 75-10%, GA300-40%, and

GA300-10% respectively. As presented in Figure 3,

for small and medium size populations, large and

small µ/λ ratios result in very similar fitness values.

IJCCI 2009 - International Joint Conference on Computational Intelligence

300

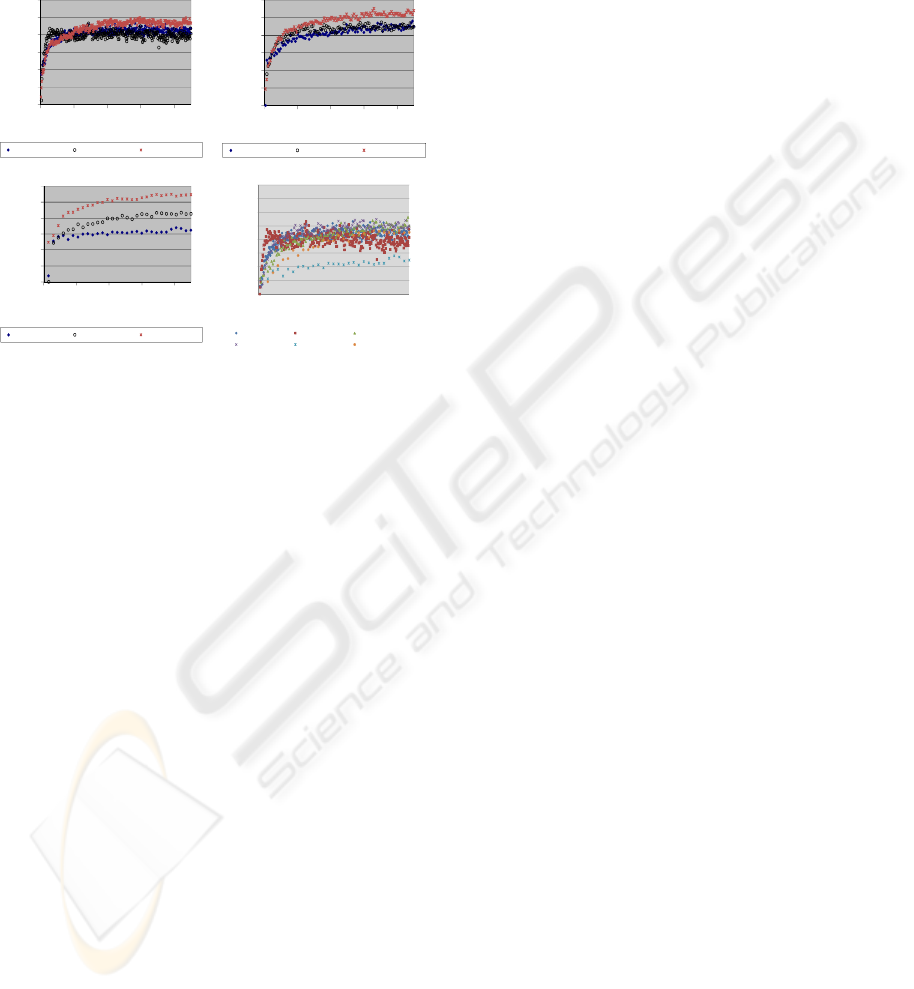
However, when the population size is 300, similar to

GA, a µ/λ ratio of 10% produces a faster increase in

fitness value. Comparing different ES settings

reveals that ES30,75, and ES7,75 produced

numerically higher fitness values compared to the

other settings tested in this study.

3500

3600

3700

3800

3900

4000

4100

0 2000 4000 6000 8000

Fitness Value

No of Fitness Function Evaluations

ES µ/λ=40% ES µ/λ=10% GA SP=40%

3500

3600

3700

3800

3900

4000

4100

0 2000 4000 6000 8000

Fitness Value

No of Fitness Function Evaluations

ES µ/λ=40% ES µ/λ=10% GA SP=10%

a) λ = 25 b) λ = 75

3500

3600

3700

3800

3900

4000

4100

0 2000 4000 6000 8000

Fitness Value

No of Fitness Function Evaluations

ES µ/λ=40% ES µ/λ=10% GA SP=10%

3700

3750

3800

3850

3900

3950

4000

4050

4100

0 2000 4000 6000 8000

Ftiness Value

No of Fi tness Function Evaluati ons

ES 25 µ/λ=40% ES 25 µ/λ=10% ES 75 µ/λ=40%

ES 75 µ/λ=10% ES 300 µ/λ=40% ES 300 µ/λ=10%

c) λ = 300 All settings

Figure 3: Effects of SP on the fitness value for different

population sizes (*GA SP=10%: GA with SP=10%).

3.3 GA vs. ES

In Figure 3 for each ES population size, the

corresponding best GA setting for that population

size is plotted. This plot shows that for all three

population sizes tested in this study, GA

outperforms ES. For small population size (25)

ES10,25 results in higher fitness values during the

first 1000 fitness function evaluations, however, for

the rest of fitness function evaluations GA 25-40%

results in numerically higher fitness values. This

observation shows that for small population sizes,

ES may be able to find a good quality answer faster

than GA. For mid-size and large size populations,

GA with 10% selection pressure clearly produces

higher fitness values than both tested settings of ES.

4 CONCLUSIONS

This paper compares the effectiveness of ES to GAs

in solving signal optimization problem. Both

algorithms were tested on a small transportation

network of nine oversaturated intersections. We

compared six different ES settings with six different

GA settings and found out that both algorithms were

capable of solving the signal optimization problem.

Findings of this study showed that, GA

outperforms ES for all three different populations

sizes tested. The setting that produced the highest

fitness values was GA with 300 population size,

10% selection pressure, two-point crossover with

probability of 85%, and simple mutation with

probability of 1%. For small population size (25),

for the first 1000 fitness function evaluations ES

provided higher fitness values than GA. However,

for the rest of fitness function evaluations (9000

total), GA outperformed ES.

In fine tuning GA, for medium size and large

size population sizes, a low selection pressure (10%)

resulted in higher fitness value due to providing

enough diversity and conducting a more

comprehensive search in the feasibility area.

However, for a small population size, a large

selection pressure (40%) provides higher fitness

values compared to a low selection pressure (10%).

Comparing the fitness values of different settings

numerically indicates that GA with 300 population

size and 10% selection pressure, outperforms all

other GA settings.

In fine tuning ES, for 25 and 75 population sizes,

both selection pressures, 40% and 10%, result in

similar fitness values. For population size equal to

300, selecting a lower selection pressure provides

higher fitness values. Comparing different ES

settings revealed that ES 30,75 and ES 7,75 resulted

in highest fitness values compared to the other

settings.

REFERENCES

Abu-Lebdeh G., Benekohal R. F., 2000. Algorithms for

Traffic Signal Control and Queue Management of

Oversaturated Two-way Arterials. Transportation

Research Record 1727.

Chang T.-H., Sun H.-Y., 2003. Modeling and

Optimization of an Oversaturated Signalized Network.

Transportation Research Part B.

Giriana M., Benekohal R. F., 2004. Using Genetic

Algorithms to Design Signal Coordination for

Oversaturated Networks. Intelligent Transportation

Systems.

Schwefel H. -P., 1992. Imitating Evolution: Collective,

Two-Level Learning Processes. Explaining Process

and Change – Approaches to Evolutionary Economics.

Te University of Michigan Press, Ann Arbor, MI.

Goldberg, D. E., Deb, K., Thierens, D., 1993. Toward a

better understanding of mixing in genetic algorithms.

Journal of the Society of Instrument and Control

Engineers.

H. Beyer, Schwefel H., 2002. Evolution Strategies A

Comprehensive Introduction. Natural Computing.

Cluwer Academic Publishers.

Sanchez Medina J., Moreno M., Royo E., 2008.

Evolutionary Computation Applied to Urban Traffic

Optimization. Advances in Evolutionary Algorithms.

EVOLUTION STRATEGIES COMPARED TO GENETIC ALGORITHMS IN FINDING OPTIMAL SIGNAL TIMING

FOR OVERSATURATED TRANSPORTATION NETWORK

301