PREDICTION OF GROUND-LEVEL OZONE

CONCENTRATIONS THROUGH STATISTICAL MODELS

J. C. M. Pires, F. G. Martins, M. C. Pereira and M. C. M. Alvim-Ferraz

LEPAE, Departamento de Engenharia Química, Faculdade de Engenharia

Universidade do Porto, Rua Dr. Roberto Frias, 4200-465 Porto, Portugal

Keywords: Air pollution modelling, Ground-level ozone, Multiple linear regression, Artificial neural networks, Multi-

gene genetic programming.

Abstract: This study aims to evaluate the performance of three statistical models: (i) multiple linear regression

(MLR), (ii) artificial neural network (ANN) and (iii) multi-gene genetic programming (MGP) for predicting

the next day hourly average ozone (O

) concentrations. O

is an important air pollutant that has several

negative impacts. Thus, it is important to develop predictive models to prevent the occurrence of air

pollution episodes with a time interval enough to take the necessary precautions. The data were collected in

an urban site with traffic influences in Oporto Metropolitan Area, Northern Portugal. The air pollutants data

(hourly average concentrations of CO, NO, NO

, NO

and O

), the meteorological data (hourly averages of

temperature, relative humidity and wind speed) and the day of week were used as inputs for the models.

ANN models presented better results in the training step. However, with regards to the aim of this study,

MGP presented the best predictions of O

concentrations (test step). The good performances of the models

showed that MGP is a useful tool to public health protection as it can provide more trustful early warnings

to the population about O

concentrations episodes.

1 INTRODUCTION

Ground-level ozone (O

) is one of the air pollutants

of most concern in Europe. It is an irritating and

reactive component in atmosphere that has negative

impacts on human health, climate, vegetation and

materials (Pires et al., 2008a). O

is the result of

three basic processes: (i) photochemical production

by the interaction of hydrocarbons and nitrogen

oxides under the action of suitable ambient

meteorological conditions (Guerra et al., 2004;

Zolghadri et al., 2004); (ii) vertical transport of

stratospheric air, rich in ozone, into the troposphere

(Dueñas et al., 2002); and (iii) horizontal transport

due to the wind that brings O

produced in other

regions. Air pollution modelling and prediction take

a great importance in preventing the occurrence of

air pollution episodes with a time interval enough to

take the necessary precautions. With regards to the

prediction of O

concentrations, several studies have

been published (Al-Alawi et al., 2008; Ozdemir et

al., 2008; Sousa et al., 2007). Artificial Neural

Networks (ANN) are often used and presented good

performances due to the nonlinearity that is

associated to the O

formation. As far it is known,

no study was performed to evaluate the performance

of MGP for predicting O

concentrations. In this

study, the aim is to compare the performances of

three models for predicting the next day hourly

average O

concentrations during seven days. The

models developed were: (i) multiple linear

regression (MLR); (ii) feedforward ANN; (iii) multi-

gene genetic programming (MGP).

2 MODELS

MLR is an extension of the simple linear regression

model for data with multiple predictor variables and

one outcome. Thus, this statistical model assumes

that the best approach to estimate the dependent

variable from the explanatory variables is to find the

linear combination of these variables that minimizes

the sum of squared errors (Pires et al., 2008b).

ANN models are characterized by a set of

processing neurons with an activation function that

are distributed in layers (input, hidden and output

layers). The neurons in the different layers are linked

551

Pires J., Martins F., Pereira M. and Alvim-Ferraz M. (2009).

PREDICTION OF GROUND-LEVEL OZONE CONCENTRATIONS THROUGH STATISTICAL MODELS.

In Proceedings of the International Joint Conference on Computational Intelligence, pages 551-554

DOI: 10.5220/0002316505510554

 SciTePress

by synapses, each one storing a weight value. These

weight values are modified during the training step

of ANN model, minimizing the value of a selected

objective function. One of the problems of the

training step is the overfitting. A high number of

iterations lead to decrease the error in the training

set, but the achieved model presents a large error

when applied to a new set. The method often applied

to solve this problem is the early stopping (Nguyen

et al., 2005; Özesmi et al., 2006). Using this method,

the data should be divided into three sets (Chiang et

al., 2004): (i) training set, used to determine the

model parameters; (ii) the validation set, used to

evaluate the performance of ANN model during the

training step and to stop it when the validation error

starts to increase; and (iii) the test set, used to

evaluate the ANN performance when applied to a

new set.

MGP is based on the principles of the simple

genetic programming (GP) algorithm (Koza, 1992).

The models are also encoded in tree structures (tree

expressions). The initial models (first generation) are

created randomly and are modified following an

iterative process, using genetic operations (selection,

crossover and mutation). The tree structures are

continuously evaluated and the fittest ones are

selected to the next iteration (elitism). This

procedure leads to optimize the model structure and

parameters, simultaneously. The iterative process

stops when a termination criterion (the achievement

of the maximum number of generations or a desired

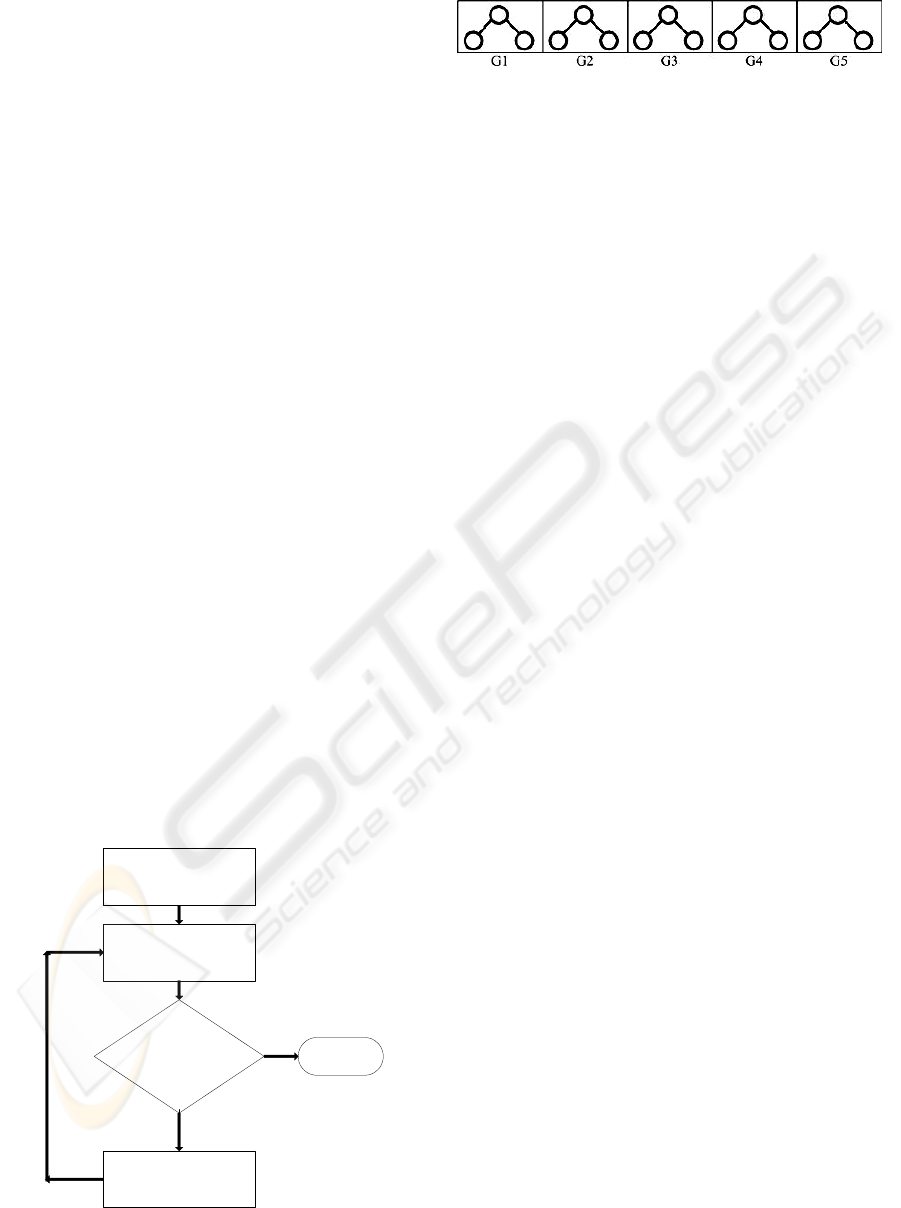
training error) is satisfied. Figure 1 summarises the

GP procedure. The main differences between GP

and MGP are: (i) a model is composed by several

tree structures, called genes, and not a single one

(see Figure 2); and (ii) the output value is calculated

Randomize the initial

population

Evaluation

Apply the genetic

operations

End

Termination

criterion satisfied?

Figure 1: GP procedure.

bbG

∑

Figure 2: MGP model codification.

through the linear combination of the outputs of the

different genes belonging to the same model (in this

study, 5 genes were applied).

3 DATA

The models considered 10 input variables: the

hourly average concentrations (in μg m

-3

) of carbon

monoxide (CO), nitrogen oxides (NO, NO

and

) and O

; hourly averages of air temperature (T),

solar radiation (SR), relative humidity (RH) and

wind speed (WS); the day of week (DW; the O

behaviour is different on weekdays and on

weekend). All environmental and meteorological

inputs corresponded to the same hour of the previous

day. The air pollution data were collected in an

urban site (Antas) with traffic influences situated in

Oporto, Northern Portugal. This site belongs to air

quality monitoring network of Oporto Metropolitan

Area that is managed by the Regional Commission

of Coordination and Development of Northern

Portugal, under the responsibility of the Ministry of

the Environment. The meteorological data were

recorded on the left edge of the Douro River, at an

altitude of 90 m approximately. These values are

representative of all Oporto Metropolitan Area. The

study period was two weeks of May 2004, where

high O

concentrations were measured and there was

no missing data. The last seven days were used for

the test period and the corresponded O

data of each

one (24 data points) were predicted using the data of

the seven days before (168 data points). For ANN

model, the validation set was 20% of the training

data. The input variables were Z standardized to

have zero mean and unit standard deviation.

4 RESULTS AND DISCUSSION

The determination of MLR models only considered

the regression parameters considered statistically

significant. The statistical significance was

evaluated through a t-test with a significance level of

0.05. The MLR models were determined using a

IJCCI 2009 - International Joint Conference on Computational Intelligence

552

0.0

4.0

8.0

12.0

16.0

20.0

D1 D2 D3 D4 D5 D6 D7

Day

RMSE

MLR

ANN

MGP

0.0

4.0

8.0

12.0

16.0

20.0

24.0

28.0

32.0

36.0

D1 D2 D3 D4 D5 D6 D7

Day

RMSE

MLR

ANN

MGP

(a) (b)

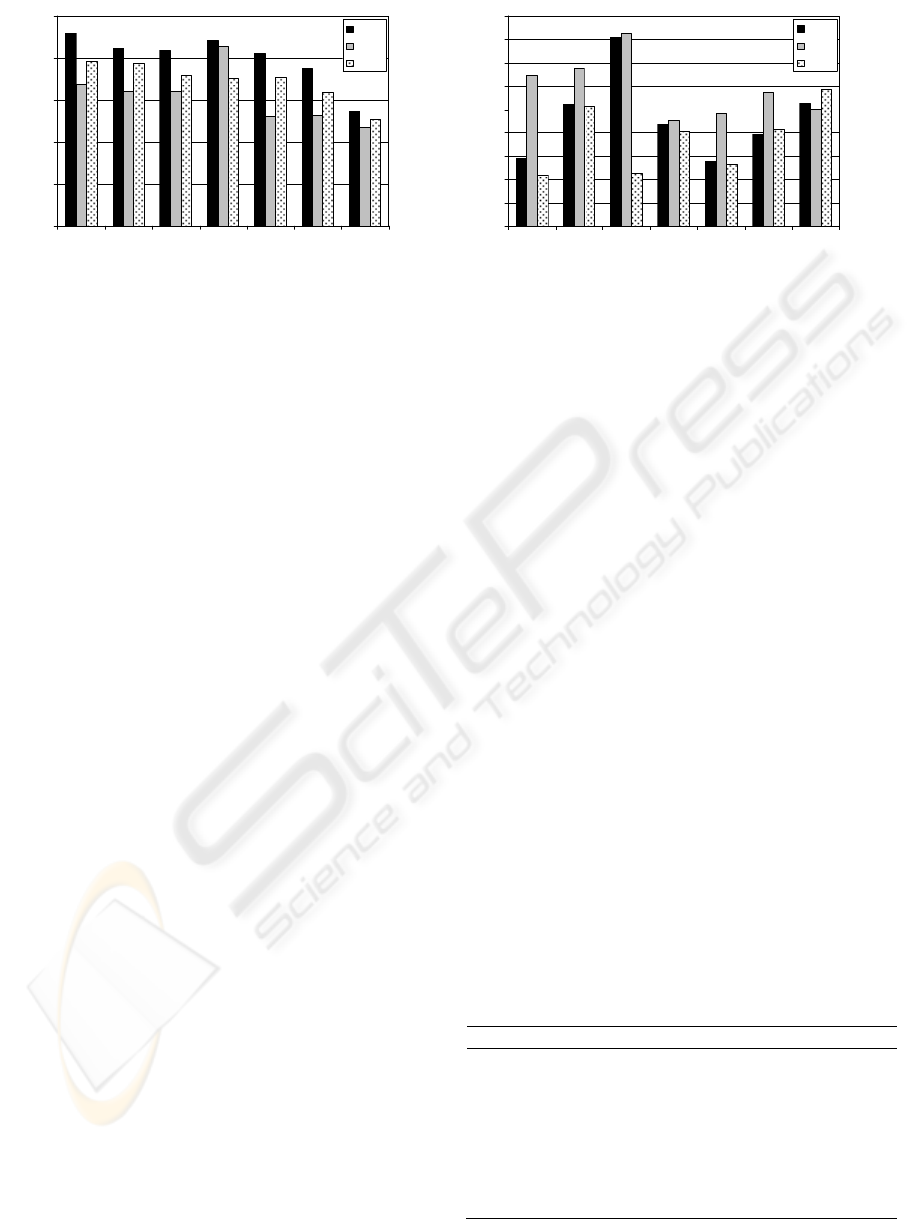
Figure 3: Performance indexes for training (a) and test (b) periods.

VBA subroutine in Microsoft Excel. In the seven

MLR models, the CO, NO, SR, WS and DW were

considered the input variables less important in the

prediction of O

concentrations. Positive correlation

coefficients were found between the predicted

variable and T, RH and O

concentrations of the

previous day, while NO

showed a negative

correlation. NO

presented positive or negative

correlation, when NO

or NO was considered

statistically significant, respectively.

Feedforward ANNs with three layers (10 input

neurons, n hidden neurons and 1 output neuron)

were also determined. Hyperbolic tangent and linear

functions were used as activation functions in hidden

and output neurons, respectively. The objective

function was the minimization of the mean squared

error of the training data. The training algorithm was

the Levenberg-Marquardt optimization. Different

ANN structures were tested, varying the number of

neurons in the hidden layer (1 to 10). For each

structure, 100 runs were performed. The best ANN

model corresponded to the minimum error in the

training and validation data. The ANN models were

determined using Matlab 7.0. In the seven ANN

models, the optimal number of hidden neurons was 5

(1 model), 7 (4 models) and 8 (2 models).

For MGP, several parameters should be defined. The

values proposed in this study are usually applied by

other authors in GP (Koza, 1992). The population

size is the number of individuals in the population;

large number of individuals increases the population

diversity, but it also increases the computation time

effort. The population size was fixed in 200 and the

maximum number of generations was 100. The

crossover and mutation rates define the probability

that an individual is selected for the crossover or

mutation operation, respectively; their values were

0.8 and 0.1. The best 10% of the best individuals (20

individuals) were selected for the next generation

(elitism). The fittest individuals were the ones

presenting the lowest root mean squared error

(RMSE; Pires et al., 2008b) in the training period.

To avoid early convergence, a new dataset for the

evaluation of individuals was created, by random

sampling the original data, with replacement when

the 20 best individuals of the actual generation were

the same of the previous one. However, in the last

10 generations the individuals were evaluated using

the original data.

The performances of all models were evaluated

using the RMSE. Figure 3 shows RMSE values for

all models in the training and test set. ANN

presented almost always the lowest training error.

However, when applied to a new set (test set), its

performance was worse than the others. Table 1

presents the models obtained to predict O

concentrations in the first day of the test set. Figure

4 shows the model predictions for the same period.

Considering whole test period, MGP presented

better predictions of O

concentrations.

Considering the flexibility for creating the

predictive models, MGP is a promising methodology

to estimate environmental complex air pollution

problems.

Table 1: Models achieved for the prediction of O

concentrations in the first day of the test period (D1).

Model

MLR

3| 24 2| |

41.8 20.3 10.5

34.5 8.2 6.0

th t xt

ttt

ONONO

TRHO

=−× +×

+×+×+×

ANN Structure: (10; 5; 1)

MGP

3| 24

24.1 7.6 tanh(cos(exp(cosh( ))))

3.5 log( ) 24.4 12.8

9.5 cosh( sin( ))

th t

tt t

TTNO

TCO

=+×

−× + ×− ×

+× −

PREDICTION OF GROUND-LEVEL OZONE CONCENTRATIONS THROUGH STATISTICAL MODELS

553

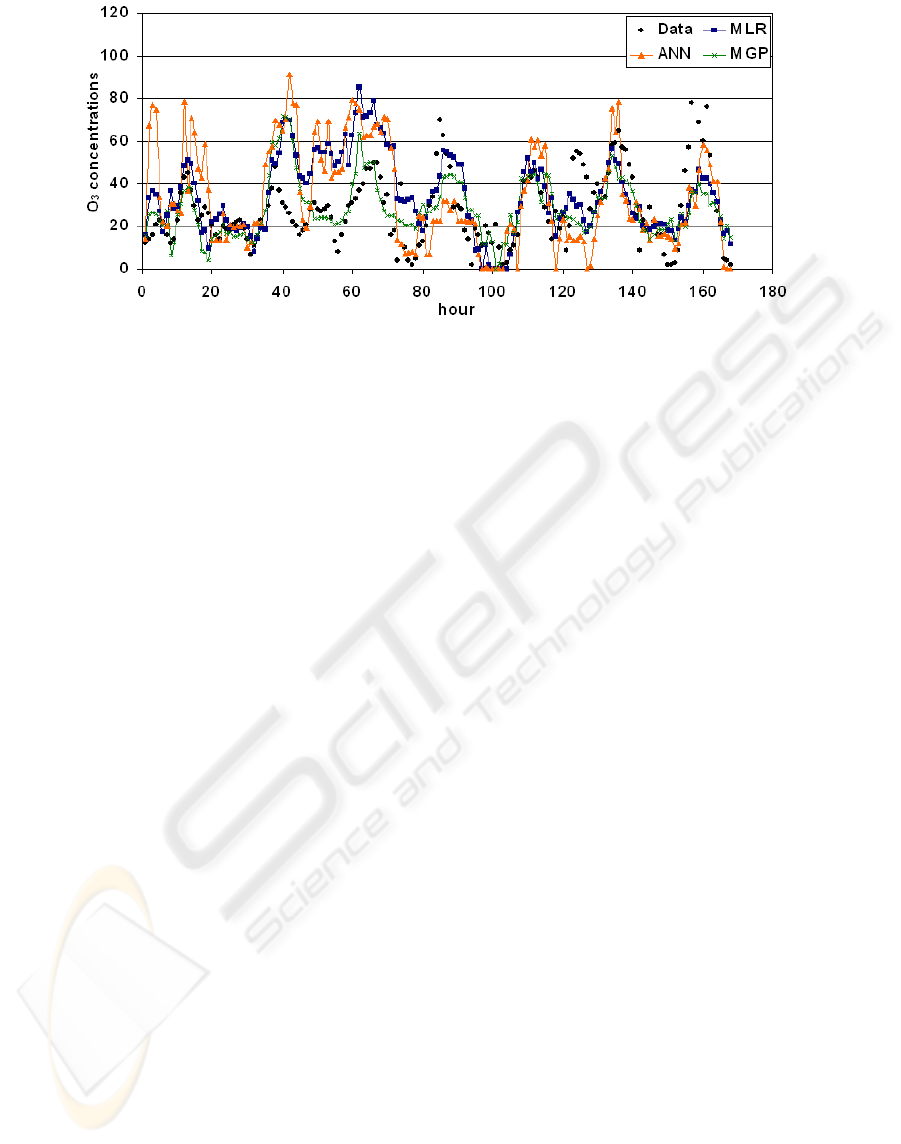
Figure 4: Prediction of O

concentrations for the test period.

5 CONCLUSIONS

Aiming the prediction of the next day hourly

average O

concentrations, the performances of

MLR, ANN and MGP were compared. The

prediction of seven consecutive days tested the

consistence of the models. ANN models presented

better results in the training step. However, with

regards to the aim of this study, MGP presented the

best predictions of O

concentrations (test set). The

good performances of the models showed that MGP

is a useful tool to public health protection as it can

provide early warnings to the population about O

concentrations episodes.

ACKNOWLEDGEMENTS

J.C.M. Pires also thanks the FCT for the fellowship

SFRH/BD/23302/2005.

REFERENCES

Al-Alawi, S.M., Abdul-Wahab, S. A., Bakheit, C. S.,

2008. Combining principal component regression and

artificial neural networks for more accurate

predictions of ground-level ozone. Environmental

Modelling & Software 23(4), 396-403.

Chiang, Y. M., Chang, L. C., Chang, F. J., 2004.

Comparison of static-feedforward and dynamic-

feedback neural networks for rainfall–runoff

modelling. Journal of Hydrology 290 (3-4), 297-311.

Dueñas, C., Fernández, M.C., Cañete, S., Carretero, J., and

Liger, E., 2002. Assessment of ozone variations and

meteorological effects in an urban area in the

Mediterranean Coast. Science of the Total

Environment 299 (1-3), 97-113.

Guerra, J.-C., Rodríguez, S., Arencibia, M.-T., García M.-

D., 2004. Study on the formation and transport of

ozone in relation to the air quality management and

vegetation protection in Tenerife (Canary Islands).

Chemosphere 56, 1157-1167.

Koza, J. R., 1992. Genetic Programming I – On the

Programming of Computers be Means of Natural

Selection, Cambridge, MA, MIT Press.

Nguyen, M. H., Abbass, H. A., McKay, R. I., 2005.

Stopping Criteria for Ensemble of Evolutionary Artifi-

cial Neural Networks. Applied Soft Computing 6 (1),

100-107.

Ozdemir, H., Demir, G., Altay, G., Albayrak, S., Bayat,

C., 2008. Prediction of Tropospheric Ozone Concen-

tration by Employing Artificial Neural Networks.

Environmental Engineering Science 25(9), 1249-1254.

Özesmi, S. L., Tan, C. O., Özesmi, U., 2006.

Methodological issues in building, training, and

testing artificial neural networks in ecological

applications. Ecological Modelling 195 (1-2), 83-93.

Pires, J.C.M., Martins, F.G., Sousa, S.I.V., Alvim-Ferraz,

M.C.M., Pereira, M.C., 2008b. Selection and

Validation of Parameters in Multiple Linear and

Principal Component Regressions. Environmental

Modelling & Software 23 (1), 50-55.

Pires, J.C.M., Sousa, S.I.V., Pereira, M.C., Alvim-Ferraz,

M.C.M., Martins, F.G. 2008a. Management of air

quality monitoring using principal component and

cluster analysis – Part II: CO, NO

and O

Atmospheric Environment 42(6), 1261-1274.

Sousa, S.I.V., Martins, F.G., Alvim-Ferraz, M.C.M.,

Pereira, M.C., 2007. Multiple linear regression and

artificial neural networks based on principal

components to predict ozone concentrations.

Environmental Modelling & Software 22(1), 97-103.

Zolghadri, A., Monsion, M., Henry, D., Marchionini, C.,

Petrique, O., 2004. Development of an operational

model-based warning system for tropospheric ozone

concentrations in Bordeaux, France. Environmental

Modelling & Software 19(4), 369-382.

IJCCI 2009 - International Joint Conference on Computational Intelligence

554