
ASSOCIATIVE SELF-ORGANIZING MAP
Magnus Johnsson, Christian Balkenius
Lund University Cognitive Science, Sweden
Germund Hesslow
Department of Experimental Medical Science, Lund, Sweden
Keywords:
Self-organizing map, Neural network, Associative self-0rganizing map, A-SOM, SOM, ANN, Expectations,
Simulation hypothesis, Cognitive modelling.
Abstract:
We present a study of a novel variant of the Self-Organizing Map (SOM) called the Associative Self-
Organizing Map (A-SOM). The A-SOM is similar to the SOM and thus develops a representation of its input
space, but in addition it also learns to associate its activity with the activity of one or several external SOMs.
The A-SOM has relevance in e.g. the modelling of expectations in one modality due to the activity invoked
in another modality, and in the modelling of the neuroscientific simulation hypothesis. The paper presents
the algorithm generalized to an arbitrary number of associated activities together with simulation results to
find out about its performance and its ability to generalize to new inputs that it has not been trained on. The
simulation results were very encouraging and confirmed the ability of the A-SOM to learn to associate the rep-
resentations of its input space with the representations of the input spaces developed in two connected SOMs.
Good generalization ability was also demonstrated.
1 INTRODUCTION
A dramatic illustration of the interaction of different
modalities can be seen in the McGurk-MacDonald
effect. If you hear a person making the sound /ba/
but the sound is superimposed on a video recording
on which you do not see the lips closing, you may
hear the sound /da/ instead (McGurk and MacDonald,
1976). The neural mechanisms underlying such in-
teraction between different sensory modalities are not
known but recent evidence suggests that different pri-
mary sensory cortical areas can influence each other.
Another familiar example is that the sensory informa-
tion gained when the texture of an object is felt in the
pocket can invoke visual images/expectations of the
object.
An efficient multimodal perceptual system should
be able to associate different modalities with each
other in this way. This provides an ability to activate
the subsystem for a modality even when its sensory
input is limited or nonexistent as long as there are ac-
tivities in subsystems for other modalities, which the
subsystem has learned to associate with certain pat-
terns of activity, which usually comes together with
the patterns of activity in the other subsystems.
This paper explores a novel variant of the Self-
Organizing Map (SOM) (Kohonen, 1988) called the
Associative Self-Organizing Map (A-SOM). The A-
SOM differs from earlier attempts to build associate
maps such as the Adaptive Resonance Associative
Map (Tan, 1995) and Fusion ART (Nguyen et al.,
2008) in that all layers (or individual networks) share
the same structure and uses topologically arranged
representations. Unlike ARTMAP, the A-SOM also
allows associations to be formed in both directions
(Carpenter et al., 1992). The A-SOM is an exten-
sion to the SOM, which learns to associate its activ-
ity with the activities of other SOMs. Previously ver-
sions of the A-SOM has been restricted to association
with only one SOM (Johnsson and Balkenius, 2008).
This work was done in the context of haptic percep-
tion where a bio-inspired self-organizing texture and
hardness perception system automatically learned to
associate the representationsof two submodalities (A-
SOMs) with each other. The system employed a mi-
crophone based texture sensor and a hardness sensor
that measured the compression of the explored ma-
terial while applying a constant pressure. It success-
fully found associated representations of the texture
and hardness submodalities when trained and tested
363
Johnsson M., Balkenius C. and Hesslow G. (2009).
ASSOCIATIVE SELF-ORGANIZING MAP.
In Proceedings of the International Joint Conference on Computational Intelligence, pages 363-370
DOI: 10.5220/0002318403630370
Copyright
c
SciTePress

with multiple samples gained from the exploration of
a set of 4 soft and 4 hard objects of different materials
with varying surface textures. However the version
of the A-SOM used in this context was only able to
associate with one SOM and its generalization ability
was not explored at all.
The A-SOM explored in this paper has been gen-
eralized to enable association with an arbitrary num-
ber of SOMs. We have tested the generalized A-SOM
with training and test sets constructed by selecting
uniformly distributed random points from a subset of
the plane, while employing Voronoi tessellations of
this plane as well as of the grid of neurons constituting
the A-SOM to determine its performance. The imple-
mentation was done in C++ using the neural modeling
framework Ikaros (Balkenius et al., 2008).
2 A-SOM
The A-SOM (Fig. 1) can be considered as a SOM
which learns to associate its activity with addi-
tional ancillary inputs from a number of additional
SOMs. It consists of an I × J grid of neurons with
a fixed number of neurons and a fixed topology.
Each neuron n
ij
is associated with r + 1 weight
vectors, where w
a
ij
∈ R
n
is used for the main in-
put and w
1
ij
∈ R
m
1
,w
2
ij
∈ R
m
2
,...,w
r
ij
∈ R
m
r
are
used for the ancillary intpus. All the elements
of all the weight vectors are initialized by real
numbers randomly selected from a uniform distri-
bution between 0 and 1, after which all the weight
vectors are normalized. At time t each neuron
n
ij
receives r + 1 input vectors x
a
(t) ∈ R
n
and
x
1
(t) ∈ R
m
1
,x
2
(t) ∈ R
m
2
,...,x
r
(t) ∈ R
m
r
.
The main net input s
ij
is calculated using the standard
cosine measurement
s
ij
(t) =
x
a
(t)w
a
ij
(t)
|x
a
(t)||w
a
ij
(t)|
, (1)
The activity in the neuron n
ij
is given by
y
ij
(t) =
y
a
ij
(t) + y
1
ij
(t) + y
2
ij
(t) + ... + y
r
ij
(t)
/(r+ 1)
(2)
where the main activity y
a
ij
is calculated using the soft-
max function (Bishop, 1995)
y
a
ij
(t) =
(s
ij
(t))
m
arg max
k
(s
k
(t))
m
(3)
where k ranges over the neurons in the neural network
and m is the softmax exponent. Like the main activ-
ity, the ancillary activity y
p
ij
(t), p = 1,2,...,r is
calculated by using the standard cosine measurement
between the ancillary inputs and the corresponding
weights.
y
p
ij
(t) =
x
p
(t)w
p
ij
(t)
|x
p
(t)||w
p
ij
(t)|
. (4)
The neuron c associated with the weight vector w
a
c
(t)
most similar to the input vector x
a
(t), i.e. the neuron
with the strongest main activation, is selected:
c = arg max
c
{||x
a
(t)w
a
c
(t)||} (5)
The weights for the main input w
a
ijk
are subsequently
adapted by
w
a
ijk
(t + 1) = w
a
ijk
(t) + α(t)G
ijc
(t)
h
x
a
k
(t) − w
a
ijk
(t)
i
(6)
where 0 ≤ α(t) ≤ 1 is the adaptation strength with
α(t) → 0 when t → ∞ and the neighbourhood func-
tion G
ijc
(t) is a Gaussian function decreasing with
time.
The weights w
p
ijl
, p = 1,2,...,r, for the ancillary in-
puts are adapted by
w
p
ijl
(t + 1) = w
p
ijl
(t) + βx
p
l
(t)
h
y
a
ij
(t) − y
p
ij
(t)
i
(7)
where β is the constant adaptation strength. All
weights w
a
ijk
(t) and w
p
ijl
(t) are normalized after each
adaptation.
3 EXPERIMENTS AND RESULTS
3.1 Associating the A-SOM with Two
Ancillary SOMs
We have evaluated the A-SOM by setting up a system
consisting of one A-SOM and two connected SOMs
(Fig. 2). To this end a set containing 10 training sam-
ples were constructed. This was done by randomly
generating 10 points with a uniform distribution from
a subset s of the plane s = {(x,y) ∈ R
2
;0 ≤ x ≤ 1,0 ≤
y ≤ 1} (Fig. 3, left). The selected points were then
mapped to a subset of R
3
by adding a third con-
stant element of 0.5, yielding a training set of three-
dimensional vectors. The reason for this was that a
Voronoi tessellation of the plane was calculated from
the generated points to later aid in the determination
of were new points in the plane were expected to in-
voke activity in the A-SOM. To make this Voronoi
tessellation, which is based on a Euclidian metric,
IJCCI 2009 - International Joint Conference on Computational Intelligence
364
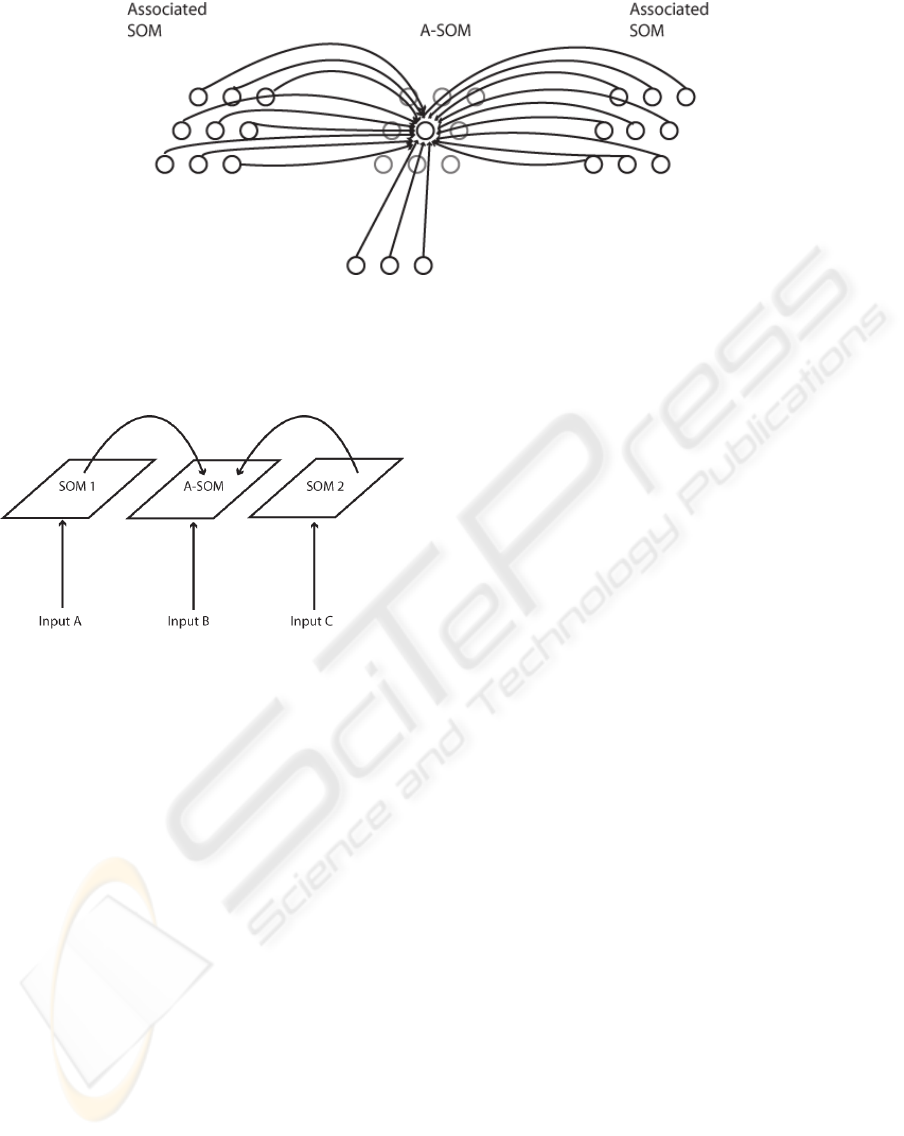
Figure 1: The connectivity of the A-SOM neural network. During training each neuron in an A-SOM receives two kinds of
input. One kind of input is the main (bottom-up) input, which corresponds to the input an ordinary SOM receives. The other
kind of input is the activity of each neuron in one or more associated ancillary SOMs. In the fully trained A-SOM, activity
can be triggered by either main input or by activity in one or several of the ancillary SOMs, or both.
Figure 2: Schematic depiction over the connections be-
tween the two SOMs and the A-SOM in the architecture of
the test system used for this paper. The test system consist
of three subsystems, which develop representations of sam-
ple sets from three input spaces (for simplicity we use the
same input set for all three representations in the study for
this paper). One of the representations (the A-SOM) also
learns to associate its activity with the simultaneous activ-
ities of the two SOMs. This means proper activity can be
invoked in the A-SOM of the fully trained system even if it
does not receive any ordinary input. This is similar to cross-
modal activation in humans, e.g. a tactile perception of an
object can invoke an internal visual imagination of the same
object.
useful for this purpose with the A-SOM, which uses
a metric based on dot product, the set of points in
the plane has to be mapped so that the corresponding
position vectors after normalization are unique. One
way to accomplish such a mapping is by adding a con-
stant element to each vector. The result of this is that
each vector will have a unique angle in R
3
. We chose
the value 0.5 for the constant elements to maximize
the variance of the angles in R
3
.
The A-SOM was connected to two SOMs (using
the same kind of activation as the main activation in
the A-SOM, i.e. dot product with softmax activation)
called SOM 1 and SOM 2, and thus also receive their
respective activities as associative input, see Fig. 2.
The A-SOM, SOM 1 and SOM 2 were then simulta-
neously fed with samples from the training set, dur-
ing a training phase consisting of 20000 iterations.
The two SOMs and the A-SOM could as well be fed
by samples from three different sets, always receiv-
ing the same combinations of samples from the three
sets (otherwise the system could not learn to associate
them). This could be seen as a way of simulating si-
multaneous input from three different sensory modal-
ities when an animal or a robot explores a particu-
lar object. Each of the three representations, the A-
SOM and the two SOMs, consists of 15× 15 neurons.
The softmax exponent for each of them were set to
1000. Their learning rate α(0) was initialized to 0.1
with a learning rate decay of 0.9999 (i.e. multiplica-
tion of the learning rate with 0.9999 in each iteration),
which means the minimum learning rate, set to 0.01,
will be reached at the end of the 20000 training iter-
ations. The neighbourhood radius, i.e. the sigma of
the neighbourhood function, was initialized to 15 for
all three representations and shrunk to 1 during the
20000 training iterations by using a neighbourhood
decay of 0.9998 (i.e. multiplication of the neighbour-
hood radius with 0.9998 in each iteration). All three
representations used plane topology when calculating
the neighbourhood. The β for the associative weights
in the A-SOM was set to 0.35.
After training the system was evaluated by feed-
ing it with samples from the training set again to one,
two or all three representations in all possible combi-
nations. When a representation did not receive any in-
put it was fed with null vectors instead (thus simulat-
ing the input of no signal from sensors of the modality
of that representation). The centers of activity in the
A-SOM as well as in the two SOMs were recorded for
ASSOCIATIVE SELF-ORGANIZING MAP
365

Figure 3: Left: The Voronoi tessellation of the points used when constructing the training set used for the A-SOM and the two
SOMs. This set was constructed by randomly generating 10 points from a subset of R
2
according to a uniform distribution.
To make this Voronoi tessellation, which is based on a Euclidian metric, valid as a measure of proximity the training set had
to be transformed by addition of a constant element to each sample vector. This is because the A-SOM using a dot product
based metric and normalizing its input would consider all position vectors of a particular angle equal. By adding a constant
element each point in the plane becomes a position vector in R
3
with a unique angle. Right: The same Voronoi tesselation
but with the points used in the generalization test depicted. Also this set was mapped to a new set in R
3
by addition of a third
constant element to each sample vector, and for the same reason as for the samples in the training set.
all these tests.
The result was evaluated by using the training set
on the fully trained system. First we recorded the cen-
ters of activation in the A-SOM when fed by main in-
put from the training set only (i.e. the two SOMs were
fed with null vectors) and the centers of activation in
the two SOMs. Then we calculated Voronoi tessel-
lations for the centers of activation in all three repre-
sentations (Fig. 4, uppermost row) to see if they could
separate the samples and in particular if the A-SOM
could separate the samples when fed by the activity
of one or both of the SOMs only. If the center of acti-
vation for a particular sample in the training set were
located in the correct Voronoi cell, this is considered
as a successful recognition of the sample, because this
means the center of activation is closer to the center
of activation of the same object than to the center of
activation of any other sample in the training set when
the A-SOM is fed by main input only like an ordinary
SOM. By comparing the Voronoi tessellations of the
A-SOM and the two SOMs (Fig. 4) and the Voronoi
tessellation of the plane for the training set (Fig. 3)
we can see that the ordering of the Voronoi cells for
the training set are to a large extent preserved for the
Voronoi cells for the centers of activation in the A-
SOM and the two SOMs. In Fig. 4 we can also see
that all, i.e. 100% of the training samples are recog-
nized in the A-SOM as long as at least one of the three
representations received input.
3.2 Generalization
To test if the system was able to generalize to a new
set of samples, which it had not been trained with,
we constructed a new set of 10 samples with the same
method as for the training set. This generalization test
set was used as input to the two SOMs and the A-
SOM, i.e. each of these representations received the
same sample simultaneously (or a null vector).
The generalization ability of the system was eval-
uated by feeding it with samples from the generaliza-
tion set to one, two or all three representations in all
possible combinations. When a representation did not
receive any input it was fed with null vectors instead.
The centers of activity in the A-SOM as well as in the
two SOMs were recorded for all these tests.
The result was evaluated by now using the gener-
alization set on the fully trained system. We recorded
the centers of activation in the A-SOM when each of
the SOMs were the only recipient of input, when both
SOMs received input, when each of the SOMs and the
A-SOM received input, when all three representations
received input, and when only the A-SOM received
input. As before a representation which did not re-
ceive input received null vectors (signifying the lack
of sensory registration for that modality). We then
looked at in which Voronoi cell the centre of activa-
tion was located in the A-SOM and in the SOMs for
each sample of the generalization set. When a gener-
IJCCI 2009 - International Joint Conference on Computational Intelligence
366

Figure 4: The center of activation for different constellations of input to the fully trained system in the A-SOM and in the two
SOMs. The centers of activation for the training samples and the generalization samples are denoted by numbers with normal
and italic typefaces respectively. Upper row left: The A-SOM when only main input to the A-SOM is received. The Voronoi
tessellation for these centers of activation has also been drawn. This is also true for the other images in this figure depicting
activations in the A-SOM. Upper row middle: The SOM1 with the Voronoi tesselation for the training set drawn. Upper row
right: The SOM2 with the Voronoi tesselation for the training set drawn. Middle row left: The A-SOM receiving main input
and the activity of SOM1. Middle row middle: The A-SOM when receiving main input and the activity of SOM2. Middle
row right: The A-SOM when receiving main input and the activities of SOM1 and SOM2. Lower row left: The A-SOM when
receiving the activity of SOM1 only. Lower row middle: The A-SOM when receiving the activity of SOM2 only. Lower row
right: The A-SOM receiving the activities of SOM1 and SOM2.
alization sample belongs to the Voronoi cell for sam-
ple k, k = 1,2, . . . ,10 of the training set (see Fig. 3)
and its activation in the A-SOM or one of the SOMs
is located in the Voronoi cell for the centre of activa-
tion for the same training sample (see Fig. 4), then we
consider the centre of activation for the generalization
sample to be properly located and we consider it to be
successfully generalized.
Leftmost in the upper row of Fig. 4 we can see
that the centers of activation for all the generaliza-
tion samples besides sample 8 is within the correct
Voronoi cell in the A-SOM when it receives main in-
put only. However that sample 8 is outside, and barely
so, the correct Voronoi cell is probably not an indica-
ASSOCIATIVE SELF-ORGANIZING MAP
367

tion that it is incorrect because the A-SOM consists
of 225 neurons and is not a continuous surface but a
discretized representation.
In the middle of the upper row of Fig. 4 we can
see that all centers of activation for the generalization
samples are correctly located in SOM1 besides 1 and
6 which are on the border to the correct Voronoi cell
(but this should probably not be considered an indica-
tion of incorrectnessfor the same reason as mentioned
above), and 2 which is located close to the correct
Voronoi cell.
Rightmost of the upper row of Fig. 4 we can
see that all centers of activation for the generaliza-
tion samples are correctly located in SOM2 besides 2,
which is located close to the correct Voronoi cell.
Leftmost in the middle row of Fig. 4 we can see
that the centers of activation for all the generalization
samples besides sample 8 (which should probably not
be considered an indication of incorrectness for the
same reason as mentioned above) is within the cor-
rect Voronoi cell in the A-SOM when it receives main
input as well as the activity of SOM1 as input.
In the middle of the middle row of Fig. 4 we can
see that the centers of activation for all the generaliza-
tion samples besides sample 8 (which should proba-
bly not be considered an indication of incorrectness
for the same reason as mentioned above) is within the
correct Voronoi cell in the A-SOM when it receives
main input as well as the activity of SOM2 as input.
Rightmost of the middle row of Fig. 4 we can see
that the centers of activation for all the generalization
samples besides sample 8 (which should probably not
be considered an indication of incorrectness for the
same reason as mentioned above) is within the correct
Voronoi cell in the A-SOM when it receives main in-
put as well as the activities of both SOM1 and SOM2
as input.
Leftmost of the lower row of Fig. 4 we can see that
the centers of activationfor all the generalization sam-
ples besides sample 2 and 10, i.e. 80%, is within the
correct Voronoi cell in the A-SOM when it receives
the activity of SOM1 as its only input.
In the middle of the lower row of Fig. 4 we can
see that the centers of activation for all the generaliza-
tion samples besides sample 2, i.e. 90%, is within the
correct Voronoi cell in the A-SOM when it receives
the activity of SOM2 as its only input.
Rightmost of the lower row of Fig. 4 we can see
that the centers of activation for all the generaliza-
tion samples besides sample 2 and 10, i.e. 80%, is
within the correct Voronoi cell in the A-SOM when it
receives the activities of SOM1 and SOM2 as its only
input.
In Fig. 5 we can see a graphical representation of
the activity in the two SOMs as well as total, main
and ancillary activities of the A-SOM while receiving
a sample from the generalization set. The lighter an
area is in this depiction, the higher the activity is in
that area.
4 DISCUSSION
We have presented and experimented with a novel
variant of the Self-Organizing Map (SOM) called the
Associative Self-Organizing Map (A-SOM), which
develops a representation of its input space but also
learns to associate its activity with the activities of
an arbitrary number of ancillary SOMs. In our ex-
periments we connected an A-SOM to two ancillary
SOMs and all these were trained and tested with a
set of random samples of points from a subset of the
plane. In addition we tested the generalization ability
of the system by another set of random points gen-
erated from the same subset of the plane. The algo-
rithm was generalized to enable association with an
arbitrary number of ancillary SOMs. Moreover this
study have also tested the ability of an A-SOM based
system to generalize its learning to new samples. The
ability of the A-SOM proved to be good, with 100%
accuracy with the training set and about 80-90% ac-
curacy in the generalization tests, depending on which
constellation of inputs which was provided to the sys-
tem. It was also observed that the generalization in
the ordinary SOMs was not perfect. If this had been
perfect the generalization ability would probably be
even better. This is probably a matter of optimizing
the parameter settings.
In this experiment we connected an A-SOM with
two SOMs, but we can see no reasons to why it should
not be possible to connect an arbitrary numbers of A-
SOMs to each other. Johnsson and Balkenius success-
fully connected two A-SOMs with each other in the
context of a hardness/texture sensing system (Johns-
son and Balkenius, 2008). In the present study we
used the same training set and the same generaliza-
tion set as input for the A-SOM and for each of the
two SOMs. This was for simplicity reasons and in
particular because it made it easier to present the re-
sults and to relate the organizations of the SOMs and
the A-SOM to each other.
It is interesting to speculate, and later test, whether
there are any restrictions on the sets that are used as
input to the different SOMs and A-SOMs in this kind
of system. A reasonable guess would be that to learn
to associate the activity arising from the training sets
impose no restrictions on the training sets, but when it
comes to generalization there would probably be one
IJCCI 2009 - International Joint Conference on Computational Intelligence
368

Figure 5: Activations at a moment in the simulation. The lighter an area is in this depiction, the higher the activity is in that
area. Upper row left: The activity in SOM1. Upper row right: The activity in SOM2. Lower row left: The total activity in the
A-SOM. Lower row, the second image from the left: The main activity in the A-SOM. Lower row, the third image from the
left: The ancillary activity in the A-SOM due to the activity in SOM1. Lower row right: The ancillary activity in the A-SOM
due to the activity in SOM2.
restriction. The restriction is that there should prob-
ably need to exist a topological function between the
different input spaces so that the sequences of input
samples from the different input spaces will invoke
traces of activities over time in their respective SOM
or A-SOM that in principle would be possible to map
on each other by using only translations, rotations,
stretching and twisting. Otherwise the generalization
would be mixed up at least partially. The same would
be true if the parameter setting implies the develop-
ment of fragmentized representations.
Our system can be seen as a model of a neu-
ral system with two monomodal representations (the
two SOMs) and one multimodal representation (the
A-SOM) constituting a neural area that merges three
sensory modalities into one representation.
The A-SOM actually develops several represen-
tations, namely one representation for its main input
(the main activity) and one representation for each of
the ancillary SOMs it is connectedto (the ancillary ac-
tivities), and one representation which merges these
individual representations (the total activity). One
could speculate whether something similar could be
found in cortex, perhaps these different representa-
tions could correspond to different cortical layers.
Interaction between sensory modalities may also
be important for perceptual simulation. An idea that
has been gaining popularity in cognitive science in
recent years is that higher organisms are capable of
simulating perception. In essence, this means that the
perceptual processes normally elicited by some ancil-
lary input can be mimicked by the brain (Hesslow,
2002). There is now a large body of evidence support-
ing this contention. For instance, several neuroimag-
ing experiments have demonstrated that activity in vi-
sual cortex when a subject imagines a visual stimulus
resembles the activity elicited by a corresponding an-
cillary stimulus (for a review of this evidence see e.g.
(Kosslyn et al., 2001); for a somewhat different inter-
pretation, see (Bartolomeo, 2002).
A critical question here is how simulated percep-
tual activity might be elicited. One possibility is that
signals arising in the frontal lobe in anticipation of
consequences of incipient actions are sent back to
sensory areas (Hesslow, 2002). Another possibility
is that perceptual activity in one sensory area can in-
fluence activity in another. The A-SOM provides a
mechanism whereby sensory activity in an artificial
system might be elicited or modulated by activity in a
different sensory modality.
It should be noted that the model presented here
is consistent with different views of how the sensory
system is organized. The traditional view of sensory
information processing has been that of a hierarchi-
cally organizedsystem. Unimodal neurons in primary
sensory cortex send signals to higher association ar-
eas where information from different modalities are
eventually merged. The model presented in this pa-
ASSOCIATIVE SELF-ORGANIZING MAP
369

per is consistent with such a view. The A-SOM in fig.
2 could be seen as being a step higher in the sensory
hierarchy than SOM-1 and SOM-2 and could project
to other A-SOMs further up the hierarchy. However,
recent neuroscientific evidence suggests that differ-
ent primary sensory cortical areas can influence each
other more directly. For instance, in a recent fMRI
study (Kayser et al., 2007) recently showed that vi-
sual stimuli can influence activity in primary auditory
cortex. The associative SOM can serve as a model
of such an organization as well. As an illustration,
SOM-1 and A-SOM in fig. 2 could be located in an
analog of a primary sensory cortical area, say an audi-
tory area, and be influenced by signals from SOM-2,
which could be located in a different, say visual, area.
In the future we will try to extend the ideas pre-
sented in this paper to beside sensory neural networks
also include motor neural networks. In this way we
hope to be able to explore the neuroscientific simula-
tion hypothesis (Hesslow, 2002).
REFERENCES
Balkenius, C., Mor´en, J., Johansson, B., and Johnsson, M.
(2008). Ikaros: Building cognitive models for robots.
In H¨ulse, M. and Hild, M., editors, Workshop on cur-
rent software frameworks in cognitive robotics inte-
grating different computational paradigms (in con-
junction with IROS 2008), Nice, France, pages 47–54.
Bartolomeo, P. (2002). The relationship between visual
perception and visual mental imagery: a reappraisal
of the neuropsychological evidence. Cortex, 38:357–
378.
Bishop, C. M. (1995). Neural Networks for Pattern Recog-
nition. Oxford University Press.
Carpenter, G., Grossberg, S., Markuzon, N., Reynolds, J.,
and Rosen, D. (1992). Fuzzy ARTMAP: A neural net-
work architecture for incremental supervised learning
of analog multidimensional maps. IEEE Transactions
on Neural Networks, 3:698–713.
Hesslow, G. (2002). Conscious thought as simulation of
behaviour and perception. Trends Cogn Sci, 6:242–
247.
Johnsson, M. and Balkenius, C. (2008). Associating
SOM representations of haptic submodalities. In Ra-
mamoorthy, S. and Hayes, G. M., editors, Towards Au-
tonomous Robotic Systems 2008, pages 124–129.
Kayser, C., Petkov, C. I., Augath, M., and Logothetis, N. K.
(2007). Functional imaging reveals visual modifica-
tion of specific fields in auditory cortex. J Neurosci,
27(1824–1835).
Kohonen, T. (1988). Self-Organization and Associative
Memory. Springer Verlag.
Kosslyn, S., Ganis, G., and Thompson, W. L. (2001). Neu-
ral foundations of imagery. Nature Rev Neurosci,
2:635–642.
McGurk, H. and MacDonald, J. (1976). Hearing lips and
seeing voices. Nature, 264:746–748.
Nguyen, L. D., Woon, K. Y., and Tan, A. H. (2008). A self-
organizing neural model for multimedia information
fusion. In International Conference on Information
Fusion 2008, pages 1738–1744.
Tan, A. H. (1995). Adaptive resonance associative map.
Neural Networks, 8:437–446.
IJCCI 2009 - International Joint Conference on Computational Intelligence
370
