
FUZZY MUTUAL INFORMATION FOR REVERSE ENGINEERING
OF GENE REGULATORY NETWORKS
Silvana Badaloni, Marco Falda, Paolo Massignan and Francesco Sambo
Dept. of Information Engineering Padova, University of Padova, via Gradenigo 6, Padova, Italy
Keywords:
Fuzzy Mutual Information, Conditional Uncertainty, Reverse Engineering.
Abstract:
The aim of this work is to provide a new definition of Mutual Information using concepts from Fuzzy Sets
theory. With this approach, we extended the model on which the well-known REVEAL algorithm for Re-
verse Engineering of gene regulatory networks is based and we designed a new flexible version of it, called
FuzzyReveal. The predictive power of our new version of the algorithm is promising, being comparable with
a state-of-the-art algorithm on a set of simulated problems.
1 INTRODUCTION
One of the main goals of studies on Genomics is
to understand the mechanism of genetic regulation,
which can be modelled as a gene regulatory network,
a graph in which nodes represent genes or proteins
and two or more nodes are connected if a regulatory
relation exists between them. A widely used approach
for inferring regulatory relations is based on the anal-
ysis of the Shannon Entropy and on the Mutual infor-
mation of gene expression signals. This mechanism
constitutes the basis of REVEAL (Liang et al., 1998),
a well-known Reverse Engineering algorithm. This
approach exploits a boolean model to represent gene
regulatory networks in which each gene is modelled
with a boolean variable True/False; its main aim is to
gather boolean relations between time series of quan-
tized gene expression values. However, the Boolean
model on which the classical REVEAL algorithm is
based is limited: a large amount of information is lost,
when a real signal is approximated with just the two
symbols 0 and 1.
In order to represent a real signal in a symbolic
qualitative way, fuzzy methodologies can provide the
basis for a more flexible model. In the present paper
we will provide a new definition of Mutual Informa-
tion in the fuzzy framework that will be used to extend
in a fuzzy direction the REVEAL algorithm. In (Co-
letti and Scozzafava, 2004) the relationship between
the notions of probability and fuzziness is deeply
studied: in particular, an interpretation of fuzzy set
theory in terms of conditional events and coherent
conditional probabilities is proposed. We will apply
this theory to re-define Mutual Information, which
will be used in the core of the REVEAL algorithm:
the modified algorithm will be called FuzzyReveal.
The paper is organized as follows: in Section 2
the concept of classical Mutual Information is re-
called and the REVEAL algorithm described, in Sec-
tion 3 first Conditional Probability is defined in terms
of membership functions, then Mutual Information
is rewritten in the new setting and the classical RE-
VEAL algorithm updated accordingly. Section 4 re-
ports an example of application.
2 MUTUAL INFORMATION AND
THE REVEAL ALGORITHM
Given a discrete random variable x, taking values in
the set X, its Shannon Entropy (Shannon, 1948) is de-
fined as
H(x) = −
∑
¯x∈X
p( ¯x)log p( ¯x),
where p( ¯x) is the probability mass function p( ¯x) =
Pr(x = ¯x), ¯x ∈ X. The joint entropy of a pair of vari-
ables x,y, taking values in the sets X,Y respectively,
is
H(x,y) = −
∑
¯x∈X,¯y∈Y
p( ¯x, ¯y)log p( ¯x, ¯y)
while the conditional entropy of x given y is defined
as
H(x|y) = H(x,y) − H(x)
25
Badaloni S., Falda M., Massignan P. and Sambo F. (2009).
FUZZY MUTUAL INFORMATION FOR REVERSE ENGINEERING OF GENE REGULATORY NETWORKS.
In Proceedings of the International Joint Conference on Computational Intelligence, pages 25-30
DOI: 10.5220/0002318800250030
Copyright
c
SciTePress

The Mutual Information of x,y is defined as
MI(x,y) = H(x) − H(x|y) and can be explicitly ex-
pressed as
MI(x,y) =
∑
¯x∈X,¯y∈Y
p( ¯x, ¯y)log
p( ¯x, ¯y)
p( ¯x)p(¯y)
≥ 0 (1)
When the two variables are independent, the joint
probability distribution factorizes and the MI van-
ishes:
p( ¯x, ¯y) = p( ¯x)p(¯y) ⇒ MI(x, y) = 0.
Mutual Information is therefore a measure of depen-
dence between two discrete random variables and is
used by the REVEAL algorithm (Liang et al., 1998)
to infer causal relations between genes: for each gene
in the genome, a time series of its rate of expression
(called gene profile) is gathered from multiple DNA-
microarray experiments; an example is depicted in
Figure 1, with time samples on the x-axis and inten-
sity of gene expression on the y-axis.
Figure 1: example of time series representing the expression
of a gene.
To apply REVEAL algorithm, gene profiles are
then quantized in two levels, 0 (underexpressed) and 1
(overexpressed), and Mutual Information is computed
between all possible pairs of genes. In the specific
case probabilities are computed as the frequencies of
the symbols 0 or 1 within a given sequence; since the
sum of the probabilities being 0 or 1 must be equal to
unity, p(1) = 1 − p(0) and the formula for the entropy
becomes:
H(x) = −p(0)· log(p(0))− (1 − p(0)) ·log(1− p(0))
The joint probability is computed as a the proba-
bility of co-occurrence of two symbols.
Example 1. Consider two random variables x and y,
representing the quantization of two time series in two
levels, 0 and 1; for each variable, consider two se-
quences of 10 symbols: x
0
= {0,1,1,1,1,1,1, 0,0, 0}
and y
0
= {0,0,0,1, 1,0, 0,1, 1,1}. Then for variable x
we obtain
p(0) = 0.4 and p(1) = 0.6 = 1 − p(0)
that means 40 % of zeros and 60% of ones respec-
tively. As for joint probabilities, in one case out of 10
∃i : x
0
i
= 0 ∧ y
0
i
= 0, therefore
p(0,0) = 0.1
The remaining combinations of symbols are
p(0,1) = 0.3, p(1, 0) = 0.4 and p(1,1) = 0.2.
The algorithm infers causal relations between
pairs whose MI is above a given threshold.
3 FUZZY EXTENSION OF THE
REVEAL ALGORITHM
The classical REVEAL Algorithm is based on a
Boolean model, therefore it has to approximate a real
signal with just two symbols 0 and 1; it is clear that in
this way much information is lost.
Using the Fuzzy Sets framework it is possible to
obtain a more flexible and expressive model.
3.1 Membership Functions and
Conditional Probability
In this paper the point of view of Coletti and Scoz-
zafava (Coletti and Scozzafava, 2002; Coletti and
Scozzafava, 2006) has been adopted.
Let x be a random quantity with range X, the fam-
ily {x = ¯x, ¯x ∈ X} is obviously a partition of the sam-
ple space Ω (de Finetti, 1970); let then ϕ be any prop-
erty related to the random quantity x: notice that a
property, even if expressed by a proposition, does not
single out an event, since the latter needs to be ex-
pressed by a non-ambiguous statement that can be ei-
ther true or false. For this reason the event referred
by a property will be indicated with E
ϕ
, meaning
“You claim E
ϕ
” (in the sense of De Finetti (de Finetti,
1970)).
Coletti and Scozzafava state that a membership
function can be defined as a Conditional Subjective
Probability between two events E
ϕ
and x = ¯x, mean-
ing that “You believe that E
ϕ
holds given x = ¯x”.
µ
E
ϕ
( ¯x) = P(E
ϕ
|x = ¯x)
The membership degree µ
E
ϕ
( ¯x) is just the opin-
ion of a real (or fictitious) person, for instance, a
“randomly” chosen one, which is uncertain about it,
whereas the truth-value of that event x = ¯x is well de-
termined in itself. Notice that conditional probabil-
ity between events E
ϕ
and x = ¯x can be directly in-
troduced rather than being defined as the ratio of the
unconditional probabilities P(E
ϕ
∧ ¯x) and P(x = ¯x).
From the same paper we report also the following ex-
ample.
IJCCI 2009 - International Joint Conference on Computational Intelligence
26

Example 2. Is Mary young? It is natural to think
that You have some information about possible val-
ues of Mary’s age, which allows You to refer to a
suitable membership function of the fuzzy subset of
“young people” (or, equivalently, of “young ages”).
For example, for You the membership function may be
put equal to 1 for values of the age less than 25, while
it is put equal to 0 for values greater than 40; then it
is taken as decreasing from 1 to 0 in the interval from
25 to 40. This choice of the membership function im-
plies that, for You, women whose age is less than 25
are “young”, while those with an age greater than 40
are not. The real problem is that You are uncertain
on being or not “young” those women having an age
between 25 and 40: the interest is in fact directed to-
ward conditional events such as E
young
|x = ¯x, with
E
young
= {You claim that Mary is young}
{x = ¯x} = {the age of Mary is ¯x}
where ¯x ranges over the interval [25, 40]. It
follows that You may assign a subjective probability
P(E
young
|x = ¯x) equal to 0.2 without any need to as-
sign a degree of belief of 0.8 to the event E
young
under
the assumption x 6= ¯x (i.e., the age of Mary is not ¯x),
since an additivity rule with respect to the condition-
ing events does not hold.
3.2 Fuzzy Mutual Information
The objective is to apply Coletti and Scozzafava the-
ory to temporal gene profiles, therefore we introduce a
set of properties Φ which describe qualitative aspects
of the profiles, such as their “height” (high, low) or
their “growth” (increasing, decreasing). Notice that
the formula for Fuzzy Mutual Information that will
be obtained is independent of the specific set chosen.
Exploiting the disintegration formula, the proba-
bility
e
P of a single event for a property ϕ ∈ Φ can be
written as
e
P(E
ϕ∈Φ
) =
∑
¯x∈X
P(E
ϕ
|x = ¯x) · P(x = ¯x)
=
∑
¯x∈X
µ
E
ϕ
( ¯x) · P(x = ¯x)
Since the Mutual Information relates two events
(in our case relates two gene profiles) let, without loss
of generalization, be Φ = {π,ρ}. In the following we
will write E
ϕ
as x = ϕ.
The conjunctive probability for x = π ∧ y = ρ
is now required. According to (Coletti and Scoz-
zafava, 2004; Coletti and Scozzafava, 2006) there is
not an unique definition for the conditional probabil-
ity P(x = π ∧ y = ρ|x = ¯x ∧ y = ¯y), called in the fol-
lowing p, for brevity. The probability p can assume
any value such that
max{µ
E
π
( ¯x) + µ
E
ρ
( ¯y) − 1, 0} ≤ p ≤ min{µ
E
π
( ¯x),µ
E
ρ
( ¯y)}
since it satisfies the coherence hypotheses (Co-
letti and Scozzafava, 2004). Notice that the bounds
for p are indeed T-Norms between the membership
functions µ
E
π
( ¯x) and µ
E
ρ
( ¯y): p may in fact range be-
tween the Lukasievicz T-Norm and the minimum; in
this work we show the results for the minimum, but
good performance was achieved with many other val-
ues, such as product, Lukasievicz or the average be-
tween Lukasievicz and minimum. The probability
that x = π ∧ y = ρ can be defined, again in virtue of
the disintegration property, as
e
P(x = π, y = ρ) =
=
∑
¯x∈X
∑
¯y∈Y
P(x = π ∧ y = ρ|x = ¯x ∧ y = ¯y)
· P(x = ¯x ∧ y = ¯y)
=
∑
¯x∈X
∑
¯y∈Y
p · P(x = ¯x,y = ¯y)
The Fuzzy Mutual Information function can now
be defined in a similar way w.r.t. the one defined
in the Probabilistic setting (Formula 1) by replacing
the probability distributions P with distributions
e
P de-
fined according to Coletti-Scozzafava’s theory.
Definition 1. Given two events x and y and a set of
symbols Φ their Fuzzy Mutual Information is defined
as
f
MI(x,y) =
∑
ϕ∈Φ
∑
ϕ
0
∈Φ
e
P(x = ϕ, y = ϕ
0
) · log
e
P(x = ϕ, y = ϕ
0
)
e
P(x = ϕ) ·
e
P(y = ϕ
0
)
This definition will be used to extend the classical RE-
VEAL algorithm.
3.3 The Algorithm
The structure of the FuzzyReveal algorithm is similar
to the classic REVEAL, but the extended definition of
Fuzzy Mutual Information is used; its pseudo-code is
reported in listing Algorithm 1.
The parameter N can be set hypothesizing a scale-
free topology for the underlying network: scale-free
networks are sparse, with a number of edges that usu-
ally lies between V and 2V , where V is the number of
nodes (Reka and Barab
´
asi, 2002).
FUZZY MUTUAL INFORMATION FOR REVERSE ENGINEERING OF GENE REGULATORY NETWORKS
27

Algorithm 1: Fuzzy Reveal.
Input: G = {x
1
,. ..,x
G
} a set of profile
sequences, Φ the set of symbols, N the
number of pairs to return
Output: the first N top-rated pairs
begin
foreach ¯g in G do
foreach ϕ in Φ do
B compute the membership
function of the profile x = ¯g w.r.t.
the property ϕ
end
end
Rank ←
/
0
foreach x, y in G : x 6= y do
foreach π, ρ in Φ do
B compute
e
P(x = π, y = ρ)
B compute
f
MI(x,x) and
f
MI(x,y)
B compute r
xy
=
f
MI(x,y)/
f
MI(y,x)
end
Rank ← Rank ∪ r
i j
end
B sort the pairs hx, yi according to Rank
return the first N pairs
end
4 EXAMPLE OF APPLICATION
The properties that have been considered to evaluate
the proposed Fuzzy Mutual Information are:
• the value of the profile x at a given point ¯x (high
or low);
• the growth behavior of the profile x (increasing or
decreasing).
For each of these four events a membership function
has been provided.
Definition 2. the set Φ
0
is the set of qualitative aspects
{”high”,”low”, ”increasing”,”decreasing”}.
The membership functions for these qualitative
aspects have been defined as
µ
high
(x) =
x
MAX
µ
low
(x) = 1 − µ
high
(x)
µ
increasing
(x) =
1 if x > S
1
x+S
0
S
1
+S
0
if − S
0
≤ x ≤ S
1
0 otherwise
µ
decreasing
(x) =
1 if x < −S
1
x−S
0
S
1
+S
0
if − S
1
≤ x ≤ S
0
0 otherwise
where MAX is the maximum among all samples;
S
1
,S
2
are thresholds that shape the trapezoids (Fig-
ure 2), and they are applied to the angular coefficients
of the series.
(a) definitions for “increasing” and “decreasing”.
(b) definitions for “high” and “low”.
Figure 2: Membership functions.
With this approach, a set of numerical values that
represent the time series can be quantified using fuzzy
levels, as in Figure 3.
Algorithm 1 has been evaluated using the Preci-
sion and Recall measures, defined as
Precision =
T P
T P + FP
Recall =
T P
T P + FN
Figure 3: Fuzzy values for two time series points.
IJCCI 2009 - International Joint Conference on Computational Intelligence
28
where T P represents the number of relations
among genes that have been correctly identified by
the algorithm (true positives), FP are the relations
found by the algorithm but not representing real re-
lations among genes (false positives), and finally FN
are the real relations that the algorithm has not been
able to find (false negatives).
To evaluate and compare the performance of dif-
ferent reverse-engineering approaches, transcriptional
networks whose interactions are perfectly known
should be used; since at present no biological net-
work is known with sufficient precision to serve as a
standard, quantitative assessment of reverse engineer-
ing algorithms can be accomplished using synthetic
networks (Grilly et al., 2007) or simulation studies
(Smith et al., 2002; Mendes et al., 2003).
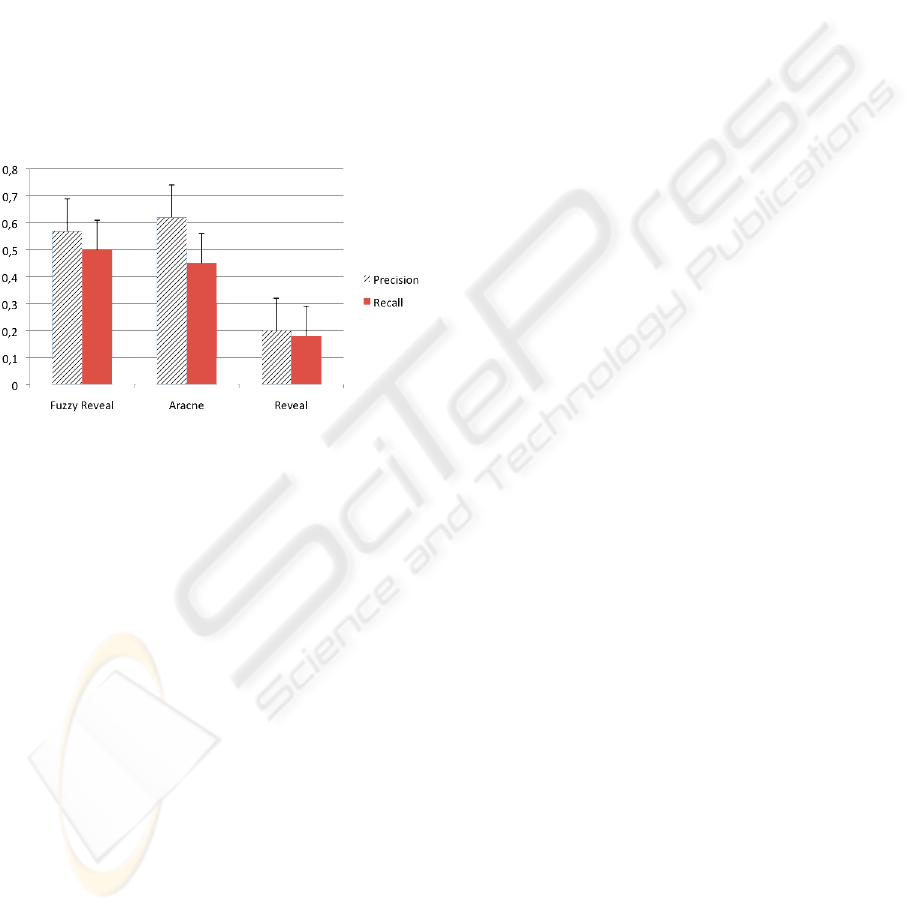
Figure 4: Precision and recall measures of FuzzyReveal,
Aracne and Classical Reveal algorithms.
To show the application of the new definition of
Mutual Information we have generated two datasets
for 12 genes and 50 time-points using an ad hoc sim-
ulator (Di Camillo et al., 2009). In Figure 4 the re-
sults are shown, together with the performances of a
“state-of-the-art” algorithm (Aracne, (Margolin et al.,
2006)) and the classical version of REVEAL. It is
possible to notice that there is a significant improve-
ment w.r.t. the classical algorithm; this is mainly
due to the fact that the classical REVEAL is based
on Boolean networks, and so it uses just two values
to represent gene expressions, while our approach al-
lows describing time series intensity in a much better
way and computing better similarity measures, since
a whole range of values from 0 to 1 is used.
The comparison with Aracne is acceptable, since
while having a slightly lower precision, it has a better
recall rate.
5 RELATED WORKS
In (Zhou et al., 2004), Mutual Information is com-
puted between quantized profiles of gene expression,
which are assigned to a fuzzy set of clusters: each
profile can belong to different clusters, with different
degrees of preference.
Fuzzy rough sets and fuzzy Mutual Information
are used in (Xu et al., 2008) for feature reduction,
when selecting potential cancer genes from DNA-
microarray experiments: given a subset of features,
new features are added to the subset if their addition
significantly increases the Mutual Information.
A Fuzzy Mutual Information measure is proposed
also in (Ding et al., 2007), where the authors follow
the approach pioneered by De Luca and Termini; ac-
cording to De Luca and Termini (De Luca and Ter-
mini, 1972) an entropy function must satisfy four
characteristic axioms, and in this way a Mutual Infor-
mation function can be built. This is similar to what
is done by Shannon using Probability theory instead
of Fuzzy sets theory.
6 CONCLUSIONS
In this paper we have considered the problem of Re-
verse Engineering and we have applied Coletti and
Scozzafava results in order to replace expression pro-
files with qualitative descriptions. These descrip-
tions are defined on a set of qualitative properties,
and can assume different membership degrees w.r.t.
a given property. Since the qualitative description
comes from a random variable whose domain is fi-
nite, all classical results of Information Theory can be
applied. We have extended the classical Mutual Infor-
mation in a fuzzy direction and we have included it in
the REVEAL algorithm thus obtaining the FuzzyRe-
veal algorithm.
As for future directions, the application of this ap-
proach to real Genomics data will be the next step of
the research. This will allow to have a better eval-
uation of performances with respect to both current
biomedical experiments and noise typical of these
data sets. A further possible improvement of this
study could be the integration of a learning module
for the automatic definition of the membership func-
tions that describe the properties of the profiles.
REFERENCES
Coletti, G. and Scozzafava, R. (2002). Probabilistic Logic
in a Coherent Setting. Kluwer Academic Publishers.
FUZZY MUTUAL INFORMATION FOR REVERSE ENGINEERING OF GENE REGULATORY NETWORKS
29

Coletti, G. and Scozzafava, R. (2004). Conditional prob-
ability, fuzzy sets, and possibility: a unifying view.
Fuzzy Sets and Systems, 144(1):227–249.
Coletti, G. and Scozzafava, R. (2006). Conditional proba-
bility and fuzzy information. Computational Statistics
& Data Analysis, 51:115–132.
de Finetti, B. (1970). Teoria della Probabilit
`
a. Einaudi,
Torino.
De Luca, A. and Termini, S. (1972). A definition of a non-
probabilistic entropy in the setting of fuzzy sets the-
ory. Information and Control, 20(3):301–312.
Di Camillo, B., Toffolo, G., and Cobelli, C. (2009). A gene
network simulator to assess reverse engineering algo-
rithms. Ann N Y Acad Sci., 1158:125–142. Annals Of
The New York Academy Of Sciences. ISSN: 0077-
8923. Accepted.
Ding, S.-F., Xia, S.-X., Jin, F.-X., and Shi, Z.-Z. (2007).
Novel fuzzy information proximity measures. Journal
of Information Science, 33(6):678–685.
Grilly, C., Stricker, J., Pang, W. L., et al. (2007). A syn-
thetic gene network for tuning protein degradation in
saccharomyces cerevisiae. Mol. Syst. Biol., 3:127.
Liang, S., Fuhrman, S., and Somogyi, R. (1998). Reveal: a
general reverse engineering algorithm for inference of
genetic network architectures. In Pacific Symposium
on Biocomputing, pages 18–29.
Margolin, A. A., Nemenman, I., Basso, K., Wiggins, C.,
Stolovitzky, G., Dalla Favera, R., and Califano, A.
(2006). Aracne: an algorithm for the reconstruction
of gene regulatory networks in a mammalian cellular
context. BMC Bioinformatics, 7.
Mendes, P., Sha, W., and Ye, K. (2003). Artificial genenet-
works for objective comparison of analysis algo-
rithms. Bioinformatics, 19:122–129.
Reka, A. and Barab
´
asi, A. L. (2002). Statistical mechanics
of complex networks. Reviews of Modern Physics,
74(1):47–97.
Shannon, C. E. (1948). A mathematical theory of commu-
nication. The Bell Systems Technical Journal, 27:379–
423.
Smith, V. A., Jarvis, E. D., and Hartemink, A. J. (2002).
Evaluating functional network inference using simula-
tions of complex biological systems. Bioinformatics,
18:216–224.
Xu, F., Miao, D., and Wei, L. (2008). Fuzzy-rough attribute
reduction via mutual information with an application
to cancer classification. Computers and Mathematics
with Applications.
Zhou, X., Wang, X., Dougherty, E. R., Russ, D., and d Suh,
E. (2004). Gene clustering based on clusterwide mu-
tual information. Journal of Computational Biology,
11(1):147–161.
IJCCI 2009 - International Joint Conference on Computational Intelligence
30
