COMPARISON OF ANFIS AND ORDINARY KRIGING

TO ASSESS HYDRAULIC HEAD DISTRIBUTION

The Orgeval Case Study

Bedri Kurtulus, Nicolas Flipo, Patrick Goblet

Centre de Géosciences, Mines ParisTech, UMR Sisyphe, 35 rue Saint-Honoré, F-77305, Fontainebleau, France

Guillaume Vilain

Université P. et M. Curie & CNRS, UMR Sisyphe 7619

Paris 6, BP 105, Tour 56-55, Etage 4, 4 Place Jussieu, 75005 Paris, France

Julien Tournebize, Gaëlle Tallec

Water Quality and Hydrology Research Unit, Cemagref, P.B. 44, 92163 Antony Cedex, France

Keywords: ANFIS, Ordinary kriging, Hydraulic head, Orgeval.

Abstract: In this study, two methods are evaluated for assessing hydraulic head distribution in an aquifer unit. These

methods consist in Ordinary Kriging (OK) and Adaptive Neuro Fuzzy based Inference System (ANFIS).

Both methods are applied on the same case study: a part of the agricultural basin of the Orgeval located 70

km east of Paris, France. 68 samples were used to predict hydraulic head distribution on a 100 m square -

grid. Cartesian coordinates of the samples were used as inputs of the ANFIS, which gives encouraging

result. Both simulations have realistic pattern (R

> 0.97) even if OK performs slightly better than ANFIS at

sampling site. Simulated hydraulic head distributions present discrepancies because the two methods

capture different patterns. Combined use of the two approaches allow for improving the sampling location

of the observation network.

1 INTRODUCTION

A hydrosystem is defined as a “part of space (where

atmosphere overlap soil surface and subsurface)

through which water flows. Physical and

biogeochemical phenomena occur in all

hydrosystem because of reactions due to water

moving through a media” (Dacharry, 1993). Many

earth scientists (hydrologists, geologists,

biogeochemists,…) do interest in understanding the

behaviour of such a complex system. Usually they

first do experiments/observations in the field at

specific locations and then try to distribute these

observations/measurements in space and time using

modelling techniques which are based on

abstractions.

In this paper our focus is to distribute punctual

hydraulic head measurements on a grid that covers a

part of an experimental basin. One technique often

used in earth sciences and especially in

hydrogeology is kriging (Flipo et al., 2007a; Renard

and Jeannée, 2008; Rivest et al., 2008). For a few

years hydrologists started to apply fuzzy logic to

transform an input signal – precipitation - to an

output signal – discharge at the outlet of a catchment

– with success (Kurtulus and Razack 2007). But

only few hydrogeology studies used soft computing

to solve their problem (Johannet et al., 2007;

Kholghi and Hosseini, 2007). The goal of this work

is to compare ordinary kriging (OK) and Adaptive

Neuro Fuzzy based Inference System (ANFIS) in

their ability to assess a hydraulic head distribution in

a complex aquifer system.

2 EXPERIMENTAL SITE

With an area of 104 km

, the Orgeval experimental

basin (Figure 1) is located 70 km east from Paris

371

Kurtulus B., Flipo N., Goblet P., Vilain G., Tournebize J. and Tallec G. (2009).

COMPARISON OF ANFIS AND ORDINARY KRIGING TO ASSESS HYDRAULIC HEAD DISTRIBUTION - The Orgeval Case Study.

In Proceedings of the International Joint Conference on Computational Intelligence, pages 371-378

DOI: 10.5220/0002319903710378

 SciTePress

Figure 1: Geology of the Orgeval basin. Sampling points (wells and springs) and gauging stations.

(Anctil et al., 2009; Flipo et al., 2007b). Agriculture

takes place on 80% of its surface while the

remaining 20% are forested. The average annual air

temperature is 9.7 ◦C. The annual mean rainfall is

706 mm, and the annual mean potential evaporation

is 592 mm. The hydrological behaviour of the

Orgeval basin is influenced by the aquifer system,

which is composed of two main geological

formations: the Oligocene (see Rupelian limestone,

Fig. 1) and the Eocene (from Priabonian to Ypresian

claystones, Fig. 1). These two aquifer units are

separated by a clayey aquitard. Most of the basin is

covered with table-land loess about 2-3m in

thickness. These unconsolidated deposits are

essentially composed of sand and loam lenses of low

permeability but they seem to be more or less

connected to the Rupelian limestone.

The basin is relatively flat with slopes increasing

near the small valley at the river mouth (80% of the

territory spans between 130 and 170 m above mean

sea level).

In this work we will focus on hydraulic head

distribution in the eastern part of the basin (Fig. 1).

3 DATA

The dataset is composed of two different types of

data (Fig. 1). The first one consists in water levels in

wells. The 61 wells were sampled on april 16, 2009

during a snapshot campaign. Our goal was to

determine the hydraulic head distribution of the

subsurface aquifer unit – silt connected to the

rupelian limestone. Due to the complex geometry of

the aquifer system at the outlet of the Avenelles

basin and in the south-eastern part of the area of

interest (Fig. 1), we needed to complete the wells

dataset in this part of the domain of interest. To do

so we used a digital elevation model (100 × 100 m)

of the top of the Priabonian mudstone. The elevation

of the limit between Priabonian mudstone and

rupelian limestone was then implemented inside the

dataset as a spring (Fig. 1). Finally the overall

dataset is composed of 68 hydraulic heads.

4 INTERPOLATION METHODS

4.1 Ordinary Kriging

Geostatistics aims at providing quantitative

descriptions of natural variables distributed in space

and time (Chilès and Delfiner, 1999). Initially

developed to address ore reserve evaluation issues in

mining (Isaaks and Srivastava, 1989), it is now

commonly applied to environmental sciences such

IJCCI 2009 - International Joint Conference on Computational Intelligence

372

as hydrogeology, air, water and soil pollution

(Goovaerts, 1997).

Geostatistics is used to characterize the spatial

structure of the variable of interest by means of a

consistent probabilistic model. This spatial structure

is characterized by the variogram, which describes

how the variability between sampled concentrations

increases with the distance between the samples. A

variogram model is fitted to the experimental

variogram for subsequent analysis.

The interpolation technique, known as kriging,

provides the ‘‘best’’, unbiased, linear estimate of a

regionalized variable at unsampled locations, where

‘‘best’’ is defined in a least squares sense, as it aims

to minimize the variance of estimation error (Chilès

and Delfiner, 1999). As for the classical

interpolations, the estimation by kriging of the

concentration at any target cell is obtained by a

linear combination of the available sample

concentrations. The kriging differentiates only by

the way of choosing the coefficients of this linear

combination. Those coefficients are called kriging

weights and depend on:

- the distances between the data and the

target (like other classical interpolators),

- the distances between the original data

themselves (data clustering),

- the spatial structure of the variable.

Exploratory data analysis, variogram fitting and

kriging were performed using the Isatis software

(Geovariances, 2008).

4.2 Adaptative Neuro Fuzzy Inference

System

Fuzzy logic (FL) was first proposed by Zadeh

(1965). It consists of three conceptual components:

(1) a rule base which contains fuzzy if–then rules,

(2) a database which defines the membership

function and (3) an inference system which

combines the fuzzy rules and produces the system

result (Firat et al., 2006). The difficulty of FL is to

determine membership function parameters and

fuzzy rules. In order to overcome this deficiency,

hybrid models (neuro-fuzzy) are generally used. It is

well understood that FL and neural networks (NN)

are complementary methodologies in the design and

implementation of intelligent systems. Each

approach has its merits and drawbacks. To take

advantage of the merits and eliminate their

drawbacks, integration of these methodologies has

been proposed by researchers during the past few

years (Cigizoglu, 2005; Özgür, 2006; Kurtulus et al.,

2008).

Adaptive neuro-fuzzy inference system (ANFIS)

is a neuro-fuzzy system developed by Roger Jang

(1992). It combines a NN and a fuzzy system

together. ANFIS uses a hybrid learning algorithm

that combines the back-propagation gradient descent

and least squares methods to create a fuzzy inference

system whose membership functions are iteratively

adjusted according to a given set of input and output

data (Jang, 1993). For each iteration, the back

propagation method involves minimization of an

objective function using the steepest gradient

descent approach in which the network weights and

biases are adjusted by moving a small step in the

direction of negative gradient. The iterations are

repeated till a convergence criteria or a specified

number of iterations is achieved. It has the

advantage of allowing the extraction of fuzzy rules

from numerical data and adaptively constructs a rule

base. (Jang, 1997).

The architecture of the ANFIS systems is

composed of five layers (Fig. 2). Each layer consists

in different nodes described by node function. The

output signal from nodes of a layer is the input

signal of the next layer. Square nodes show

parameter sets that are adjustable. These nodes are

called adaptive nodes. Circle nodes represent

parameter sets that are constant. These nodes are

called fixed nodes. More details on ANN and

ANFIS are available in Tagaki, 1985; ASCE, 2000;

Pratihar, 2008; Zadeh, 2008.

The neuro fuzzy model were developed using the

ANFIS procedures of MATLAB (Demuth and

Beale, 2003). In this study, a code is written in

Matlab 7.0 for ANFIS using appropriate functions to

calculate the best performance of the methods.

The dataset is divided into 3 subsets for training,

validation and test of the neuro-fuzzy model. Input

data are XY coordinates of the springs and wells.

Hydraulic head is the ANFIS output.

Figure 2: ANFIS architecture (x, y: inputs, A1 and B1:

linguistic labels (low, medium, high, etc.), N: node,

Layer1: generate of membership grades, Layer 2: Fuzzy

rules Layer 3: ratio of the rules named firing strength,

Layer 4: product of the normalized firing strength, Layer

5: fuzzy results transformed into a traditional output).

COMPARISON OF ANFIS AND ORDINARY KRIGING TO ASSESS HYDRAULIC HEAD DISTRIBUTION - The

Orgeval Case Study

373

Before using the model to interpolate unknown

outputs (hydraulics head), its actual predictive

performance must be tested by comparing outputs

estimated by the calibrated models with known

outputs. At each phase (training, validation), the

ANFIS performance is measured by the

determination coefficient of goodness-of-fit R

, and

the root mean square error (RMSE).

It is recommended to normalize the data between

slightly offset values such as 0.1 and 0.9. The

dataset is normalized to be consistant with ANFIS’s

output that lies in the interval [0, 1]. It is also due to

the fact that inputs and outputs usually have

different unit and are then not homogoneous. The

last reason is that membership functions are also

included in the interval [0,1]. One way to scale input

and output variables in interval [0.1, 0.9] is called

pre-processing. In this work the preprocessing is

done with a simple linear transformation. Let call X

the input vector with n coordinates ranging from X

min

to X

max

. Each coordinate (j) of the transformed

variable Y is calculcated following the equation:

()

minmax

9.01.08.0

XXX

−+

−

(1)

The selection of appropriate input parameters is a

complex task. The first step is to determine the

number of training and validation data. This

selection was done iteratively in the following way:

• The area of interest is divided in for squares of

equal size.

• If a square contains three points then two are

selected for the training set and one for the

validation set. Else the square is divided in four

squares of equal size and so on.

Finally the dataset was split into two sets: 60 % of

the data were assigned to the training set and the

remaining to the validation and test set (20% each).

Early stopping criteria provided by the validation

datasets are used to prevent overtraining.

Generalized bell curves were used as membership

functions.

5 INTERPOLATION OF

HYDRAULIC HEAD: RESULTS

AND DISCUSSION

For each method (ANFIS and kriging) the hydraulic

head distribution was calculated on a 100 m square

grid.

5.1 Kriging

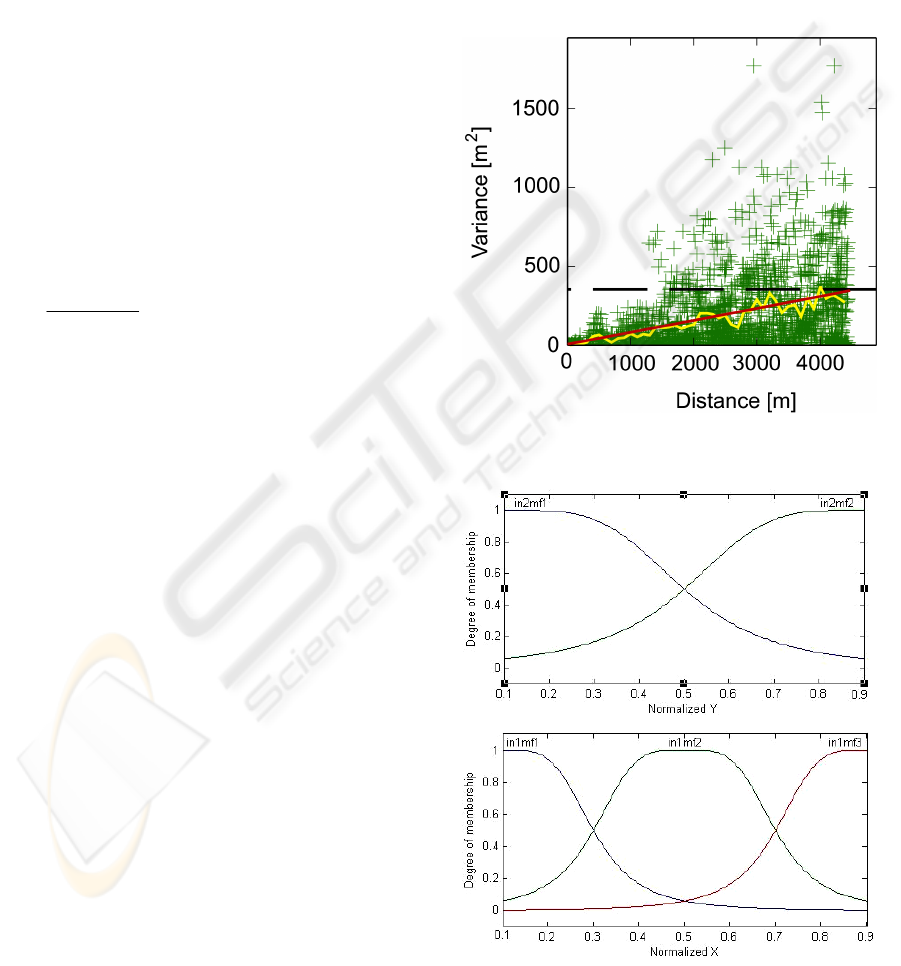
First of all the variographic clouds and the

associated experimental variograms were calculated

with different ranges (50 m, 100 m, 200 m and 1

km). They all reveal a clear linear structure (See Fig.

3 for a 250m range). The fitted variogram reveals a

sill at 354.6 m

with a scale of 5000 m (Fig. 3). The

fitted variogram was then used to krige the hydraulic

head at each center of the 100 m scare grid. Figure

6a shows the result of the kriging.

Figure 3: Variogram cloud (green crosses), experimental

variogram (yellow line) and modeled variogram (red line).

Figure 4: Membership functions (after 44 iterations).

IJCCI 2009 - International Joint Conference on Computational Intelligence

374

5.2 Anfis

The best calibrated ANFIS model is obtained after

44 iterations. It contains 5 membership functions

and 6 rules. Figure 4 shows the membership

functions at the end of the learning phase.

5.3 Comparison of the Interpolation

Methods

In this section observed and simulated data are

compared. Table 1 summarizes statistics on

observed and simulated data for each type of

simulation: ANFIS and OK. Table 2 shows statistics

on residuals at each cell of the grid containing a well

or a spring. Root mean square errors (RMSE), Mean

Error (ME), Mean Absolute Error (MAE) and

coefficient of determination (R

) were calculated for

ANFIS and OK.

Table 1: Observed and simulated data statistics. SD:

standard deviation.

Observed ANFIS Kriging

Values at sampling points

Mean [m] 139,49 139,47 139,33

Min [m] 102,00 107,73 102,42

Max [m] 179,85 181,03 179,47

SD [m] 20,05 19,91 19,90

All Grid

Mean [m] - 101,78 102,42

Min [m] - 193,65 181,05

Max [m] - 143,83 141,89

SD [m] - 20,54 18,14

Table 2: Statistics of errors for ANFIS and OK.

ANFIS OK

RMSE [m] 3,30 0,77

ME [m] -0,03 -0,16

MAE [m] 2,47 0,55

0,97 0,99

Table 1 shows statistics of both series (observed and

predicted hydraulics head). The minimum,

maximum, average and standard deviation values are

of the same magnitude for simulations (whatever the

techniques) and for the observed values. Even if the

two methods match properly the data (Fig. 5) with

of 0.97 for ANFIS and 0.99 for OK, the

comparison of performances (Table 2) indicates a

slight advantage for kriging. Indeed RMSE for

ANFIS and OK are 3.3 m and 0.8 m, respectively.

Figure 5: Observed vs simulated hydraulics heads.

After being compared with observations at each

sample location, each method is used to interpolate

the dataset at each cell center of a 100m grid (Fig.

6). It is then interesting to remark that the hydraulic

head distributions have similarities and few

differences far from sampling points. The Average

values of the whole set is 102.4 m for ANFIS

whereas OK calculates an average of 101.8 (Table

1). The standard deviation of the ANFIS

interpolation increases (19.9 to 20.5 m) whereas the

one of OK decreases (19.9 to 18.1).

Both simulations have realistic pattern except

few details as local minima. Even if OK performs

slightly better than ANFIS, the latter seems to be a

valuable way of extrapolating hydraulics head but

not a more efficient method than OK as stated by

Kholghi & Hosseini (2008).

The fact that a few ANFIS estimates are far from

the observed values (Fig. 5) may be due to the input

variables (X and Y coordinates) of the ANFIS.

Indeed these inputs do not have any physical

meaning considering the hydraulic head distribution,

which is partly driven by the river network. For

further work one should test the euclidian distance to

the river associated to only one coordinate (either X

or Y) as input variables. The comparison of

hydraulic head distributions calculated by OK and

ANFIS (Fig. 6a & 6b) indicates that the two

techniques capture the phenomenon in two different

ways.

The less sampling points, the more different are

the estimates. Kriging is really sensitive to the

variogram that depends on the number of sampling

points. In the Avenelles basin there are only 68

sampling points. The fitted variogram might entail

considerable uncertainty. Using this variogram for

OK leads to biased results (Pardo-Iguizquiza et al.,

2009). To our knowledge ANFIS was used only

once by Kholghi & Hosseini (2008). This is not

enough to draw conclusion.

COMPARISON OF ANFIS AND ORDINARY KRIGING TO ASSESS HYDRAULIC HEAD DISTRIBUTION - The

Orgeval Case Study

375

Figure 6: (a) Kriging interpolation and (b) ANFIS interpolation.

At this point, it is not possible to determine the best

interpolation technique but one can use them to

improve measurement network based on

discrepancies between the two estimates (Fig. 7).

The discrepancy map indicates in black and deep

blue the area where sampling should be achieved in

order to understand which method do perform best

for the Orgeval aquifer unit.

6 CONCLUSIONS

AND PERSPECTIVES

This paper focuses on the comparison of Adaptive

Neuro-Fuzzy Interface System (ANFIS) and

Ordinary Kriging (OK) to interpolate hydraulics

head in the Avenelles aquifer system. Both methods

provide satisfactory estimates even if they catch two

different representation of the phenomenon. On the

one hand, X and Y coordinates were used as input

variables of the ANFIS and may be improved by

using the distance to the river instead of one of them.

On the other hand kriging gives results entailed with

a large uncertainty far from sampling points. It is not

possible to determine which method performs best

but the combined use of both methods may help to

improve the observation network.

The next step of this work will be to obtain a

consistent hydraulic head distribution in the basin.

This consistent field will then be used as a reference

to apply inverse methods on the basin which will

allow to determine physical parameter distribution in

the experimental site.

Finally ANFIS could be a possible alternative

method to kriging in the case of discontinuities or in

highly heterogeneous media. For instance, the

building of the heterogeneous structure of an aquifer

system is still a research topic for hydrogeologist,

geomorphologists and other earth science

researchers.

IJCCI 2009 - International Joint Conference on Computational Intelligence

376

Figure 7: Difference between OK and ANFIS estimates.

ACKNOWLEDGEMENTS

This work was funded by the ANR Carnot Institut,

the PIREN Seine research program, and the FIRE

(Federation Ile de France de Recherche en

Environnement). It is also a contribution to the GIS

Oracle that maintains the experimental basin of the

Orgeval. We kindly thank the BRGM for providing

the DEM of the top of the aquifer system.

REFERENCES

ASCE Task Committee, 2000, Artificial neural networks

in hydrology-I: Preliminary concepts, J. Hydrol. Eng.

5(2): 115–123

Anctil, F., Filion, M. and Tournebize, J., 2009. A neural

network experiment on the simulation of daily nitrate-

nitrogen and suspended sediment fluxes from a small

agricultural catchments. Ecol Model 220: 879–887.

Chilès, J.-P., Delfiner, P., 1999. Geostatistics: modeling

spatial uncertainty.Wiley, New York.

Cigizoglu, H.K., 2005, Generalized regression neural

network in monthly flow forecasting. Civil Enginee-

ring and Environmental Systems, 22(2):71-84.

Dacharry, M., 1993. Encyclopédie AXIS.

Demuth H and Beale M., 2003, ‘Neural networks toolbox’

user guide. Mathworks Inc., Natick, MA.,

U.S.A.

Firat, M., Gungor, M., 2007, River ﬂow estimation using

adaptive neuro fuzzy inference system Mathematics

and Computers in Simulation. 75: 87–96.

Flipo, N., Jeannée, N., Poulin, M., Even, S., Ledoux, E.,

2007a, Assessment of nitrate pollution in the Grand

Morin aquifers (France): Combined use of

geostatistics and physically based modelling.

Environmental Pollution 146, 241-256. doi:10.1016/

j.envpol.2006.03.056.

Flipo, N., Even, S., Poulin, M., Théry, S., Ledoux, E.,

2007b, Modeling nitrate fluxes at the catchment scale

using the integrated tool CAWAQS. Sci Total

Environ. 375, 69-79.

Geovariances 2008, Isatis Technical References, version

8, 148 p.

Goovaerts, P., 1997. Geostatistics for Natural Ressources

Evaluation. Oxford University Press, New York, 181

pp.

Isaaks, E., Srivastava, R., 1989. An Introduction to

Applied Geostatistics. Oxford University Press.

Jang, J.S.R., 1992, Self-learning fuzzy controllers based

on temporal back propagation, IEEE Trans. Neural

Networks. 3 (5) 714–723

Jang, J.S.R.., 1993, ANFIS adaptive-network-based fuzzy

inference systems, IEEE Trans. Systems, Man Cybern.

23 (03) 665–685

Jang, J. S. R., 1997, Neuro-Fuzzy and Soft Computing,

Prentice-Hall, New Jersey.

Johannet, A., Ayral, P.A., Vayssade, B., 2007, Modelling

non measurable processes by neural network:

Forecasting underground flow – Case study of the

COMPARISON OF ANFIS AND ORDINARY KRIGING TO ASSESS HYDRAULIC HEAD DISTRIBUTION - The

Orgeval Case Study

377

Cèze Basin (Gard – France). Advances and

Innovations in Systems, computing sciences and

software engineering. 53-58

Kholghi, M., Hosseini, S.M., 2008, Comparison of

Groundwater Level Estimation using Neuro-fuzzy and

Ordinary Kriging. Environmental Modeling and

Assessment doi - 10.1007/s10666-008-9174-2

Kurtuluş B., Razack M., 2007, Evaluation of the ability of

an artificial neural network model to simulate the

input-output responses of a large karstic aquifer. The

La Rochefoucauld (Charente, France), Hydro-geology

Journal (15) 2:241-254.

Kurtuluş, B., 2008, Modelling of Groundwater Flow and

Quality in Karstic Systems Using Soft Computing

Methods (Neural Networks, Fuzzy Logic, Ph.D.

Thesis Hacettepe Univeristy Institute of Graduate

Studies in Science and Engineering and Poitiers

University, Faculty of Fundamental and Applied

Science, Ankara-Poitiers, 163p.

Özgür, K., 2006, Suspended sediment estimation using

neuro-fuzzy and neural network approaches

Hydrological Sciences. 50(4): 683-696.

Pardo-Iguzquiza, E., Chica-Olmo, M., Jose Garcia-

Soldado, M., Luque-Espinar, J. A., 2009, Using

Semivariogram Parameter Uncertainty in

Hydrogeological Applications. Ground Water 47(1),

25-34.

Pratihar, D. K., 2008, Soft Computing. Alpha Science

International Ltd. 229p.

Renard, F., Jeannée, N., 2008, Estimating transmissivity

fields and their influence on flow and transport: The

case of Champagne mounts. WRR 44, W11414,

doi:10.1029/2008WR007033.

Rivest, M., Marcotte, D., Pasquier, P., 2008,Hydraulic

head field estimation using kriging with an external

drift: A way to consider conceptual model

information. Journal of Hydrology 361, 349– 361

Takagi, T., Sugeno, M., 1985, Fuzzy identification of

systems and Its applications to modeling and control,

IEEE Trans. Systems Man and Cybernetics 15(1):

116-132

Zadeh, L.A., 1965, Fuzzy sets. Information and Control.

8:338-353

Zadeh L.A., 2008, Is there a need for fuzzy logic?

Information Sciences. 178: 2751–2779

IJCCI 2009 - International Joint Conference on Computational Intelligence

378