RECURSIVE SELF-ORGANIZING NETWORKS FOR PROCESSING

TREE STRUCTURES

Empirical Comparison

Pavol Vanˇco and Igor Farkaˇs

Department of Applied Informatics, Comenius University, Mlynsk´a dolina, Bratislava, Slovak Republic

Keywords:

Recursive self-organizing networks, Tree structures, Output representation.

Abstract:

During the last decade, self-organizing neural maps have been extended to more general data structures, such

as sequences or trees. To gain insight into how these models learn the tree data, we empirically compare

three recursive versions of the self-organizing map – SOMSD, MSOM and RecSOM – using two data sets

with the different levels of complexity: binary syntactic trees and ternary trees of linguistic propositions.

We evaluate the models in terms of proposed measures focusing on unit’s receptive ﬁelds and on model’s

capability to distinguish the trees either in terms of separate winners or distributed map output activation

vectors. The models learn to topographically organize the data but differ in how they balance the effects of

labels and the tree structure in representing the trees. None of the models could successfully distinguish all

vertices by assigning them unique winners, and only RecSOM, being computationally the most expensive

model regarding the context representation, could unambiguously distinguish all trees in terms of distributed

map output activation.

1 INTRODUCTION

During the last decade, there has been an extensivere-

search activity focused on extending self-organizing

networks to more general data structures, such as se-

quences or trees; for overviewof approaches see (Bar-

reto et al., 2003) and (Hammer et al., 2004b). The

widely used self-organizing map (SOM) (Kohonen,

1990) has been originally formulated for vectorial

data (i.e. for inputs belonging to a vector space of a

ﬁnite and ﬁxed dimension). One way that allows nat-

ural processing of structured data with modiﬁed ver-

sions of SOM is to equip it with additional feedback

connections. No prior metric on the structured data

space is imposed, instead, the similarity measure on

structures evolves through parameter modiﬁcation of

the feedback mechanism and recursive comparison of

constituent parts of the structured data. Typical early

examples of these models are the temporal Kohonen

map (TKM) (Chappell and Taylor, 1993), and the re-

current SOM (RSOM) (Koskela et al., 1998). They

contain units functioning as leaky integrators of their

past activations, i.e. each unit has only a feedback

from itself. This restriction was overcome in subse-

quent models, e.g. SOM for structured data (SOMSD)

(Hagenbuchner et al., 2003), merge SOM (MSOM)

(Strickert and Hammer, 2005) and recursive SOM

(RecSOM) (Voegtlin, 2002). These models transcend

the simple local recurrence of leaky integrators and

due to a more complex feedback they can represent

richer dynamical behavior (Hammer et al., 2004b).

It is known that when applied to sequences, the

organization of unit’s receptive ﬁelds in these recur-

sive SOM models becomes topographic and typically

has Markovian nature: Sequences with similar most

recent entries tend to have close representations in

the map. In case of MSOM it was shown that se-

quences are represented by means of exponentially

weighted summation of their input vectors (Hammer

et al., 2004b). In RecSOM, however, also a non-

Markovian dynamics was observed in case of a com-

plex symbolic sequence such as the English text (Tiˇno

et al., 2006). This implies a broken topography of

unit’s receptive ﬁelds: two sequences with the same

sufﬁx can be mapped to distinct positions on the map,

separated by a region of very different sufﬁx structure.

A few years ago, extensions of these models to tree-

structured data have been submitted for investigation

(Hagenbuchner et al., 2003; Hammer et al., 2004b).

The natural questions arise about how these models

459

Van

co P. and Farkaš I. (2009).

RECURSIVE SELF-ORGANIZING NETWORKS FOR PROCESSING TREE STRUCTURES - Empirical Comparison.

In Proceedings of the International Joint Conference on Computational Intelligence, pages 459-466

DOI: 10.5220/0002320104590466

 SciTePress

learn to organize their receptive ﬁelds and what is

their capacity in representating the trees.

In this paper, we attempt to provide answers to

these questions by testing the three above mentioned

SOM models (brieﬂy introduced in Section 2) that

differ by the complexity of the context representation.

SOMSD uses a reference to the winner position in the

grid, MSOM refers to the winner content, and Rec-

SOM refers to the whole map activation. Unlike se-

quences that have linear structure, the symbolic struc-

tures naturally imply more complexity in data organi-

zation and, as we will explain later, one can differenti-

ate between the content and the structure in a tree. For

the purpose of empirical comparison, we propose two

pairs of related quantitative measures (Section 3). We

assess and compare the performanceof the three mod-

els on two data sets that differ in complexity: binary

syntactic trees and ternary trees of linguistic proposi-

tions (Section 4).

2 MODELS

As proposed in (Hammer et al., 2004a), all three

models can be generalized to processing n-ary trees

(n = 1 applies to sequences). In each model, a unit

i ∈ {1, 2,...,N} in the map has n + 1 weight vectors

associated with it: w

∈ R

– weight vector linked

with an M-dimensional input s(t) feeding the net-

work at time t, and c

( j)

– jth context weight vector

(j = 1,2,...,n) linked with the context whose dimen-

sionality is model-dependent.

For each model, the distance of unit i from a tree

at time t is computed as

(t) = αks(t) − w

+ β

∑

j=1

ch( j)

− c

( j)

(1)

where parameters α > 0 and β > 0 respectively inﬂu-

ence the effect of the current input and the context on

the neuron’s proﬁle, k.k denotes the Euclidean dis-

tance, ch( j) denotes the winner index for jth child,

( j)

is ith context (weight) vector of jth child, and

ch( j)

is the (model-speciﬁc) context representation.

For SOMSD, p

ch( j)

≡ r

ch( j)

is a two-dimensional

vector (we assume 2D maps) with integer compo-

nents specifying the winner location in the grid. For

MSOM, p

ch( j)

≡ q

ch( j)

, where the so called context

descriptor of jth child is computed as

ch( j)

= (1− γ) w

ch( j)

+ γ

∑

′

( j

′

)

ch( j)

Hence, the dimensionality of q

ch( j)

equals input di-

mension M. Finally, for RecSOM, p

ch( j)

≡ y =

,...,y

] is the output activation of RecSOM with

components

(t) = exp(−d

(t)). (2)

The dimensionality N of the p

ch( j)

(for each child)

makes RecSOM computationally the most expensive

architecture. The activation function in Eq. 2 is also

used for the other two models to provide map output

activation vectors that we need for model comparison.

Learning of both input and context weights in each

model has the same Hebbian form as in the standard

SOM (Hammer et al., 2004a):

∆w

= µ h(i,i

∗

) (s(t) − w

∆c

( j)

= µ h(i,i

∗

) (p

ch( j)

(t) − c

( j)

)

where j = 1, 2,...,n, the winner i

∗

= argmin

(t)},

µ is the learning rate, h(i,i

∗

) = exp(−d(i,i

∗

)/σ

) is

the neighborhood function that uses d(.,.) as the Eu-

clidean distance of the two units in the lattice. The

“neighborhood width”, σ, linearly decreases to allow

forming topographic representation of the trees.

3 PERFORMANCE MEASURES

In order to evaluate the model performance we intro-

duced two pairs of related numerical measures. The

ﬁrst measure was inspired by the quantizer depth in-

troduced for symbolic sequences for quantifying the

amount of memory captured by the map (Voegtlin,

2002). It is deﬁned as the average size of the unit’s re-

ceptive ﬁeld, i.e. the common sufﬁx of all sequences

for which that neuron becomes the winner. In case

of trees, we propose an analogue named Tree Quan-

tizer Depth (TQD), computed as the average size of

Tree Receptive Field (TRF), i.e. the common “sufﬁx”

(subtree) of all vertices for which that neuron is the

winner. Hence,

TQD =

∑

i=1

(3)

where p

is the probability of unit i becoming a winner

(in a given data set) and s

is the (integer) size of its

TRF. TQD is sensitive to the content (of tree leaves)

and returns the value of an averagetree depth captured

by the individual map units (functioning as subtree

detectors).

Unlike sequences, which have linear structure,

trees provide room for distinguishing between the

content (captured by TQD) and the structure only.

This leads to the second measure, the Structure-only

sensitive TQD (STQD), which detects the structure of

a tree by only distinguishing between the leaves and

IJCCI 2009 - International Joint Conference on Computational Intelligence

460

the inner nodes, not between the nodes with different

labels (i.e. their content). (For example, a unit can be-

come sensitive to a tree (a(b –)), i.e. it is insensitive

to the contents of the right child, being an inner tree

node). STQD is deﬁned as

STQD =

∑

i=1

′

(4)

where s

′

denotes STRF of ith neuron and p

is the

same as above.

The other pair of measures was introduced to

quantify the discrimination capacity of the models to

unambiguously represent different trees. This implies

the ability to uniquely represent all vertices (subtrees)

contained in all trees (Hammer et al., 2004b). One

view of the vertex representation is in terms of a sep-

arate winner reserved for it. The alternative view is

based on a distributed representation of vertices that

entails the overall map output activation. The pro-

posed measures focus on these alternatives.

So, the third measure – the winner differentiation

(WD) refers to the level of winners and is computed

as the ratio of the number of different winners inden-

tiﬁed and the number of all different subtrees in the

data set (including the leaves), that is

WD =

|{ j|∃t : j = i

∗

(t)}|

|{vertices in data set}|

. (5)

WD<1 indicates that not all vertices could be distin-

guished by the map (i.e. two or more different vertices

would share the winner). The fourth, more “detailed”

measure looks at the differences between map output

activation vectors, and yields the difference between

the two most similar representations (probably corre-

sponding to two very similar trees such as (v(d(an))

and (v(dn))). We will refer to this measure as the nor-

malized minimum Euclidean distance

MED = argmin

u6=v

{ky(T

) − y(T

)k/N}, (6)

where y(T

) is the map output activation vector

(whose components are obtained using Eq. 2) cor-

responding to processing of the root of the tree T

MED>0 implies that all vertices can be distiguished

in terms of map output activation vectors.

4 EXPERIMENTS

We tuned the model parameters experimentally ac-

cording to the task difﬁculty. We started with ba-

sic maps of 10×10 units in case of binary trees and

15×15 units for ternary propositions. We looked for

the models with the best discrimination capacity as

determined by the largest number of unique winners

in representing different vertices (captured by WD

measure). We also tested larger maps with 225 and

400 units using the optimal parameters (α,β) found

for the initial map size. In MSOM, the parameter

of the context descriptor was set to its default value

γ = 0.5 in both experiments. In all simulations, the

leaves were assigned localist (one-hot) codes (to be

treated as symbols). We systematically searched the

(α,β) parameter space, as each model can trade-off

the effect of leaves and contexts. It was observed that

increasing α (while keeping β constant) did not affect

output representations of leaves but led to the overall

decrease of activations for trees. Increasing β (with

constant α) led to gradual vanishing of output repre-

sentations of leaves, and to focusing of activations for

trees (and also vanishing in combination with higher

α).

4.1 Binary Syntactic Trees

This data set contained 7 syntactic trees with labeled

leaves and unlabeled inner nodes (vertices) (Table 1).

The trees were generated by a simple grammar origi-

nally developed for testing the representational capac-

ity of the Recursive Auto-Associative Memory (Pol-

lack, 1990). For the RAAM, being a two-layer per-

ceptron trained as auto-associator, the ability to repre-

sent a tree involvesits successful encoding (at the hid-

den layer) and the subsequent unambiguous decoding

(at the output layer). In case of our unsupervisedfeed-

back maps, there is only the encodingpart. The ability

of the map to represent a tree implies its ability to also

uniquely represent all vertices (subtrees) contained in

the training set (listed in the right half of Table 1).

Similarly to RAAM, processing a tree in a feed-

back map proceeds bottom-up from the leaves, for

which context activations are set to zero vectors, up to

the root. When processing the inner nodes, the inputs

s(t) are set to zero vectors. Intermediate results (ac-

tivations p

ch( j)

) are stored in a buffer to be retrieved

later. The weights are updated in each discrete step.

The models were trained for 2000 epochs. During

the ﬁrst 60% of epochs, the neighborhood width was

set to linearly decrease, σ:3→0.5 (ordering phase),

and was then kept constant (ﬁne-tuning phase). For

the larger maps the initial neighborhood width was

proportionally increased and the proﬁle was kept the

same. The learning rate linearly decreased µ:0.3→0.1

during the ordering phase, and was then kept constant.

For the best models of all sizes, we present the four

quantitative measures (averaged over 100 runs) in Ta-

bles 2 and 3 and also the (typical) graphical informa-

tion about unit weights and output activations. Stan-

RECURSIVE SELF-ORGANIZING NETWORKS FOR PROCESSING TREE STRUCTURES - Empirical Comparison

461

Table 1: Binary trees used for training and the list of vertices comprised by the data set.

Training set Vertices contained in it

(d(a(a(an)))) ((dn)v) (an) (p(dn))

((dn)(p(dn))) ((dn)(v(d(an)))) (a(an)) (d(an))

(v(dn)) ((d(an))(v(p(dn)))) (a(a(an))) (v(d(an)))

(p(d(an))) (dn) (v(p(dn)))

(dn)

(an)

(v(p(dn)))

((dn)v)

(p(d(an)))

(a(a(an)))

(v(d(an)))

(d(a(a(an))))

(a(an))

((dn)(v(d(an))))

(v(dn))

(d(an))

(p(dn))

((dn)(p(dn)))

((d(an))(v(p(dn))))

Figure 1: Output activities of SOMSD for all vertices from

the binary trees data set (α = 0.5, β = 0.9).

0.5

1.5

Distance

(d(a(a(an))))

(a(a(an)))

(a(an))

(v(dn))

((dn)(p(dn)))

((d(an))(v(p(dn))))

(d(an))

(p(d(an)))

(v(d(an)))

(v(p(dn)))

((dn)v)

((dn)(v(d(an))))

(dn)

(p(dn))

(an)

Figure 2: Dendrogram of SOMSD output activations for all

vertices from the binary trees data set.

Figure 3: Converged (a) input, (b) left context and (c) right

context weights of the SOMSD model trained on the binary

trees. Topographic organization is evident in all cases.

dard errors were negligible in all cases except MED

in SOMSD. All these characteristics illustrate model’s

behavior and together facilitate model comparison.

SOMSD. The best results for SOMSD were obtained

using α = 0.5 and β = 0.9. The average percent-

age of (possible) unique winners was almost 93%

(Table 3). The errors were caused by similar trees

(such as (a(an)) and (v(dn))) that shared the win-

ners. The SOMSD output activity (Figure 1) and the

unit’s weight proﬁles (Figure 3) clearly show the to-

pographic organization in which the winners for leaf

nodes are clearly separated from winners for trees. In

addition, simpler trees, located in the upper left area,

are separated from the more complex trees in the bot-

tom right area of the map. It can also be observed

that activation proﬁles for trees are more focused than

proﬁles for leaves. The corresponding dendrogram of

the map activity (Figure 2) reveals how the map dif-

ferentiates between the trees. Leaves are differenti-

ated from non-trivial trees with an exception of (an)

which is the simplest tree. Increasing the map size

was observed to lead to an improvement (Table 3): all

20 trees could be, with a rather high reliability, dis-

tinguished in the map. Only SOMSD displayed non-

zero variability of all measures.

((d(an))(v(p(dn))))

((dn)(v(d(an))))

((dn)(p(dn)))

(dn)

(d(a(a(an))))

((dn)v)

(d(an))

(an)

(a(an))

(a(a(an)))

(v(p(dn)))

(v(d(an)))

(v(dn))

(p(d(an)))

(p(dn))

Figure 4: Output activities of MSOM for all vertices from

the binary trees data set (α = 0.2,β = 1.0).

MSOM. As seen in Figure 4, winners for leaves (triv-

ial trees) are again well separated from units repre-

senting trees. There are only 80% of different win-

ners, because each neuron becomes activated for sev-

eral inputs – the MSOM activation is much more

widespread than in the case of SOMSD (and Rec-

SOM).

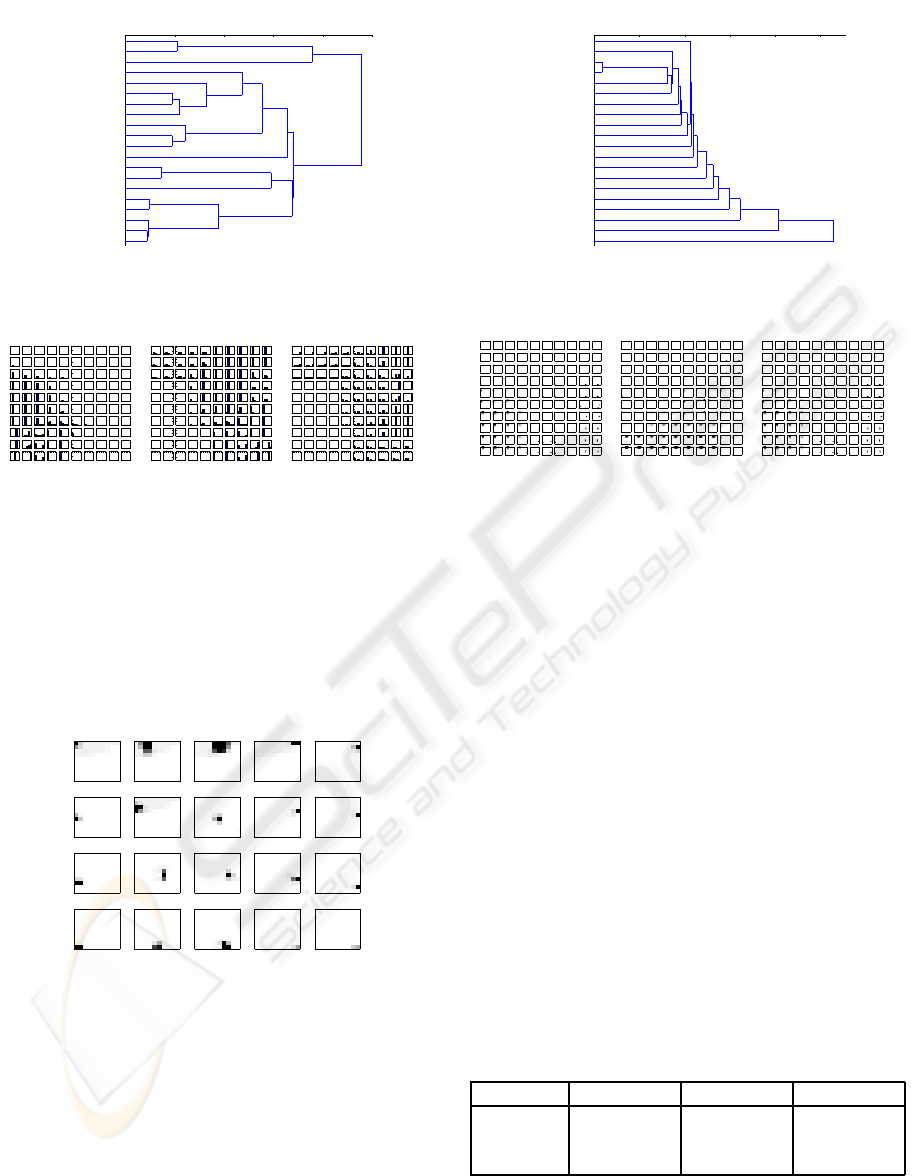
Even though the dendrogram (Figure 5) shows

that MSOM differentiates between leaves and non-

trivial trees, the trees are differentiated differently

from SOMSD model. The weight proﬁles (Figure 6)

split the map in representing leaves and inner nodes.

The differences between the left and the right contexts

are due to the asymmetry of the trees in the data set

IJCCI 2009 - International Joint Conference on Computational Intelligence

462

0.5

1.5

2.5

Distance

(d(a(a(an))))

(d(an))

(dn)

((dn)(p(dn)))

((dn)(v(d(an))))

((d(an))(v(p(dn))))

((dn)v)

(a(a(an)))

(a(an))

(an)

(p(dn))

(p(d(an)))

(v(dn))

(v(d(an)))

(v(p(dn)))

Figure 5: Dendrogram of MSOM output activations for all

vertices from the binary trees data set.

Figure 6: Converged (a) input, (b) left context and (c) right

context weights of the MSOM model trained on the binary

trees.

(left and right children). Increasing the map size to

225 units led to an improvement of all measures (ex-

cept MED). Further increase to 400 units (i.e. almost

the double size) did not improve any measure value.

The problem for all MSOMs was to differentiate be-

tween (v(d(an))) and (v(dn))) even in this simple data

set.

((d(an))(v(p(dn))))

((dn)v)

(v(dn))

(p(d(an)))

(v(d(an)))

(an)

(p(dn))

(a(an))

(a(a(an)))

(v(p(dn)))

(dn)

(d(a(a(an))))

(d(an))

((dn)(v(d(an))))

((dn)(p(dn)))

Figure 7: Output activities of RecSOM for all vertices from

the binary trees (α = 1.6, β = 0.9).

RecSOM. Best results were achieved with α = 1.6

and β = 0.9. This parameter combination differs from

the other two models due to the opposite α:β ratio.

The likely reason is that higher value of α in Rec-

SOM is needed to counterbalance the effect of high-

dimensional context activations. Nevertheless, the

output activations of leaf nodes remained very weak

even after training. The whole map activity (Fig-

ure 7) is more focused than in the case of MSOM and

SOMSD but there are more different winners, 95%

0.5

1.5

2.5

Distance

(d(a(a(an))))

(a(an))

((dn)(p(dn)))

((dn)(v(d(an))))

(v(p(dn)))

((d(an))(v(p(dn))))

(v(dn))

(v(d(an)))

(p(d(an)))

((dn)v)

(a(a(an)))

(p(dn))

(an)

(dn)

(d(an))

Figure 8: Dendrogram of RecSOM output activations for

all vertices from the binary trees data set.

Figure 9: Converged (a) input, (b) left context and (c) right

context weights of the RecSOM model trained on the binary

trees. The context weights are displayed as 2D mesh plots.

on average for the initial map size. The dendrogram

of RecSOM (Figure 8) is different from the previous

models because the differentiation is not hierarchical

and some leaves are mingled with trees. The reason

lies in highly focused output activations. The weight

proﬁles (Figure 9) show that units focusing on leaves

are again well separated from units focusing on trees.

As with SOMSD, increasing the map size to 225 units

led to maximum WD = 1.0 (100%) and to an increase

of MED as well.

In all models, the values of TQD and STQD mea-

sures are quite similar suggesting that for this data set

the models do not differ in the average depth of their

unit’s receptive ﬁelds. These values are close to 3,

i.e. an average unit is sensitive to a vertex with two

children. In addition, STQD is simular to TQD which

implies that maps did not develop detectors sensitive

for tree structures only. The likely reason is a low

number of leaves and a small size of the data set.

Table 2: TQD and STQD (in parantheses) measures for the

models trained on the binary trees.

Model 10×10 15×15 20×20

SOMSD 2.82 (2.92) 2.93 (2.93) 2.93 (2.93)

MSOM 2.61 (2.66) 2.86 (2.86) 2.86 (2.86)

RecSOM 2.83 (2.86) 2.93 (2.93) 2.93 (2.93)

RECURSIVE SELF-ORGANIZING NETWORKS FOR PROCESSING TREE STRUCTURES - Empirical Comparison

463

Table 3: WD and MED (in parantheses) measures for the models trained on the binary trees.

Model 10×10 15×15 20×20

SOMSD 0.93 (0.003±0.002) 1.00 (0.0005) 0.99 (0.002±0.001)

MSOM 0.80 (0.002) 0.95 (0.002) 0.95 (0.001)

RecSOM 0.95 (0.0008) 1.00 (0.004) 1.00 (0.002)

4.2 Ternary Linguistic Propositions

This data set originated from English sentences that

were generated using a probabilistic context-free

grammar with semantic constraints and were then

rewritten into ternary propositions. The translation

process resulted in 307 various (non-trivial)trees with

maximum depth 7. Table 4 lists a few examples

of used sentences and their translations to proposi-

tions.

. Some trees have empty inner nodes (NULL

labels). The ﬁfty words (i.e. leaves) in the lexicon

yield M = 50. We trained the maps with 15× 15 units

for 20 epochs. The neighborhood size was set to

σ:5→0.5 over 12 epochs and then remained constant.

For larger maps, σ was proportionally increased. The

learning rate was set to µ:0.3→0.1 over 12 epochs,

and was then kept constant.

(feeds, boy, (is, cat, (sees, John, cat)))

feeds

boy

(is, cat, (sees, John, cat))

cat

(sees, John, cat)

sees

John

(walks, (is, Kate, (hears, John, Kate)), dog)

walks

(is, Kate, (hears, John, Kate))

dog

Kate

(hears, John, Kate)

hears

(hates, (is, John, (sees, boy, John)), Mary)

hates

(is, John, (sees, boy, John))

Mary

(sees, boy, John) (walks, Steve, −)

Steve

(bark, (are, dogs, (see, dogs, girl)), −)

bark

Figure 10: Output activities of SOMSD for 25 randomly

selected vertices from the ternary trees data set. Longer tree

labels are positioned below the corresponding image.

SOMSD. For the best map (α = 0.5,β = 0.4), almost

20% of all inputs had a unique winner. The SOMSD

behavior clearly differentiates between leaves and

non-trivial trees (Figure 10). The winners for leaves,

located in the lower right corner, show little differ-

ences in their map output representations. In the case

of leaves the activity of the map is less focused than

for more complex trees. The more complex a tree, the

more focused activity is devoted to it in the map. A

In translation, the word who was replaced by the heads

is and are depending on the subject number used in the

phrase. For a sentence with maximum embedding of depth

n, the tree depth is 2n + 1.

more detailed analysis revealed that SOMSD learned

to differentiate non-trivial trees based on depth

, as

predicted in (Hammer et al., 2004b). The number

of winners in SOMSD oscillated between 71 and 66.

Despite fewer winners, the runs with 66 winners (30%

of cases) yielded better results in terms of TQD and

STQD. Increasing the map size to 20×20 led to an

increase of all measures except MED that remained

0. This means that SOMSD cannot distinguish some

inputs even at the level of the map activation.

(feeds, boy, (is, cat, (sees, John, cat)))

feeds

boy

(is, cat, (sees, John, cat))

cat

(sees, John, cat)

sees

John

(walks, (is, Kate, (hears, John, Kate)), dog)

walks

(is, Kate, (hears, John, Kate))

dog

Kate

(hears, John, Kate)

hears

(hates, (is, John, (sees, boy, John)), Mary)

hates

(is, John, (sees, boy, John))

Mary

(sees, boy, John)

(walks, Steve, −)

Steve

(bark, (are, dogs, (see, dogs, girl)), −)

bark

Figure 11: Output activities of MSOM for 25 randomly se-

lected vertices from the ternary trees data set. Longer tree

labels are positioned below the corresponding image.

(feeds, boy, (is, cat, (sees, John, cat)))

feeds

boy

(is, cat, (sees, John, cat))

cat

(sees, John, cat)

sees

John

(walks, (is, Kate, (hears, John, Kate)), dog)

walks

(is, Kate, (hears, John, Kate))

dog

Kate

(hears, John, Kate)

hears

(hates, (is, John, (sees, boy, John)), Mary)

hates

(is, John, (sees, boy, John))

Mary

(sees, boy, John)

(walks, Steve, −)

Steve

(bark, (are, dogs, (see, dogs, girl)), −)

bark

Figure 12: Output activities of RecSOM for 25 randomly

vertices from the ternary trees data set. Longer tree labels

are positioned below the corresponding image.

Illustrating dendrograms for this data set are not in-

cluded here due to space limitations.

IJCCI 2009 - International Joint Conference on Computational Intelligence

464

Table 4: Examples of simpler generated sentences and their translations.

Sentence Proposition

Steve walks (walks Steve NULL)

women see boys (see women boys)

dogs who pl see girl bark (bark (are dogs (see dogs girl)) NULL)

boy feeds cat who John sees (feeds boy (is cat (sees John cat)))

MSOM. The best results were achieved for α = 0.4

and β = 0.6. Parameter β needed to be slightly larger

than in SOMSD, because the context weights have

higher dimension. It can be seen that MSOM activ-

ity (Figure 11) is quite different from that of SOMSD.

The whole map is activated for every input although

most of the neurons show only low activity. Leaves

are located in the lower right part of the map and

non-trivial trees are scattered throughout the rest of

the map. The analysis of output activation dendro-

grams revealed that MSOM differentiates trees with

respect to both labels and the depth. Regarding the

labels, the ﬁrst (topmost) word (being a verb) be-

came the clustering parameter. The best result for

MSOM was 53 distinct winners (8.3%) which is far

below SOMSD. Both memory depth measures were

even further decreased after enlarging the map size to

20×20 units. Based on these measures, the perfor-

mance of the MSOM model was the worst among all

models for the ternary trees data set.

RecSOM. The best results for RecSOM were

achieved for α = 2.4 and β = 0.4. The map activa-

tions (Figure 12) are more focused for both leaves and

trees to the previous models, and also the organiza-

tion of output space is very different. Leaves are not

located in one part of the map but are scattered across

the map. The leaves usually have different represen-

tations than the rest of inputs. As in previous models,

both the most recent inputs and the structure are im-

portant for the map activation. Regarding the output

activations, both the structure and RFs inﬂuence the

output representations.

In sum, regarding the memory depth, the mod-

els already show differences in terms of TQP, where

RecSOM ranks ﬁrst. In addition, values for STQD

are signiﬁcantly higher in all models which implies

that units also developed sensitivity to structures. The

reason may be in both higher number of possible

trees and the number of leaves such that units can

no longer cope with the content sensitivity given the

available resources (number of units). Regarding the

uniqueness of representations, with respect to win-

ners, SOMSD was the best model for this data set.

However, RecSOM was the only model that achieved

MED>0, i.e. was able to distinguish every single ver-

tex in terms of map output activation. We can con-

Table 5: Average TQD and STQD (in parantheses) mea-

sures for all models trained on the ternary trees data set.

Model 15× 15 20× 20

SOMSD 1.10 (2.65) 1.14 (2.90)

MSOM 0.76 (1.63) 0.54 (1.67)

RecSOM 1.17 (1.69) 1.40 (2.26)

Table 6: Average WD and MED (in parantheses) measures

for all models trained on the ternary trees data set.

Model 15×15 20×20

SOMSD 0.195 (0.0) 0.241 (0.0)

MSOM 0.083 (0.0) 0.050 (0.0)

RecSOM 0.160 (1.4×10

−6

) 0.171 (2.4×10

−6

)

clude that RecSOM beneﬁts from the higher complex-

ity of its context representation.

It is true that SOMSD is computationally the most

efﬁcient architecture and was even advocated as the

most appropriate model (Hammer et al., 2004b) judg-

ing from comparisons in representing company lo-

gos (presented as tree structures). Our simulations

favour RecSOM, instead, since the high complexity

of its context representation seems justiﬁed in case of

ternary propositions. Of course, further simulations

are required to verify these claims.

5 CONCLUSIONS

The goal of this paper was to shed light onto how dif-

ferent recursive SOM models process tree structured

data. We compared the performance of these mod-

els using four proposed quantitative measures. With

respect to content memory depth (TQD), it is not

possible to say which model performs best regarding

both data sets because the performance of RecSOM

and SOMSD is comparable. Regarding the structure

(STQD), SOMSD yields the best results suggesting

that it can cluster the trees very well according to their

structural properties. The models differ in the way

how they distinguish the trees. For SOMSD, the tree

structure is more important than the content (of the

labels), but the content also plays a role within the

same structure. MSOM clusters the trees in the map

more preferably by the content than SOMSD but the

RECURSIVE SELF-ORGANIZING NETWORKS FOR PROCESSING TREE STRUCTURES - Empirical Comparison

465

structure is also important. RecSOM model creates a

complex organization of tree representations based on

both the structure and the content.

Regarding the uniqueness of output representa-

tions, it turns out that the winner position is only suf-

ﬁcient in the case of simple tree data sets such as the

binary syntactic trees. Although according to the the-

oretical claim (Hammer et al., 2004b) we should only

need a sufﬁcient number of neurons to unambigu-

ously represent all vertices, our experimental simula-

tions suggest that the sufﬁcient map size is the neces-

sary but not the sufﬁcient condition. The problem ap-

pears to lie in ﬁnding weights (by training) that would

lead to unique winners. Therefore, we have to employ

the map output activation for tree representation, as

suggested by simulations. However, this only helps

in case of RecSOM that yields nonzero differences in

all pairs of map output activations for both data sets.

Hence, RecSOM beneﬁts from higher complexity of

its context representation.

Understanding how recursive SOMs (and neural

networks in general) learn to represent the data struc-

tures is not only important for practical tasks, but also

in cognitivescience as a principled paradigm based on

neural computation. Connectionist models have been

criticised for lacking important representational prop-

erties (that can be found in symbolic models) such as

those needed for systematic representation and pro-

cessing of structures (Fodor and Pylyshyn, 1988).

Nevertheless, neural networksdo offer the potential to

process symbolic structures employing various types

of recursive architectures (Hammer, 2003). However,

further investigations are needed.

ACKNOWLEDGEMENTS

This work was supported by Slovak Grant Agency for

Science. I.F. is also part-time with Institute of Mea-

surement Science, Slovak Academy of Sciences.

REFERENCES

Chappell, G. J. and Taylor, J. G. (1993). The temporal Ko-

honen map. Neural Networks, 6:441–445.

de A. Barreto, G., Ara´ujo, A., and Kremer, S. (2003). A tax-

onomy of spatiotemporal connectionist networks re-

visited: The unsupervised case. Neural Computation,

15:1255–1320.

Hagenbuchner, M., Sperduti, A., and Tsoi, A. (2003). A

self-organizing map for adaptive processing of struc-

tured data. IEEE Transactions on Neural Networks,

14(3):491–505.

Hammer, B., Micheli, A., Sperduti, A., and Strickert, M.

(2004a). Recursive self-organizing network models.

Neural Networks, 17(8-9):1061–1085.

Hammer, B., Micheli, A., Strickert, M., and Sperduti, A.

(2004b). A general framework for unsupervised pro-

cessing of structured data. Neurocomputing, 57:3–35.

Kohonen, T. (1990). The self-organizing map. Proceedings

of the IEEE, 78(9):1464–1480.

Koskela, T., Varsta, M., Heikkonen, J., and Kaski, K.

(1998). Time series prediction using recurrent SOM

with local linear models. International Journal of

Knowledge-Based Intelligent Eng. Systems, 2(1):60–

68.

Strickert, M. and Hammer, B. (2005). Merge SOM for tem-

poral data. Neurocomputing, 64:39–72.

Tiˇno, P., Farkaˇs, I., and van Mourik, J. (2006). Dynam-

ics and topographic organization in recursive self-

organizing map. Neural Computation, 18:2529–2567.

Voegtlin, T. (2002). Recursive self-organizing maps. Neural

Networks, 15(8-9):979–992.

Pollack, J. (1990). Recursive distributed representations.

Artiﬁcial Intelligence, 46(1-2):77–105.

Fodor, J.A., and Pylyshyn, Z.W. (1988). Connectionism and

cognitive architecture: A critical analysis. Cognition,

28: 3–71.

Hammer, B. (2003). Perspectives on learning symbolic

data with connectionistic systems. In: Adaptivity and

Learning, Springer, 141–160.

IJCCI 2009 - International Joint Conference on Computational Intelligence

466