
A HYBRID ANT COLONY OPTIMIZATION ALGORITHM FOR
SOLVING THE TERMINAL ASSIGNMENT PROBLEM
Eugénia Moreira Bernardino, Anabela Moreira Bernardino
Department of Computer Science, School of Technology and Management, Polytechnic Institute of Leiria, Leiria, Portugal
Juan Manuel Sánchez-Pérez, Juan Antonio Gómez-Pulido, Miguel Angel Vega-Rodríguez
Dep. of Technologies of Computers and Communications, Polytechnic School, University of Extremadura, Cáceres, Spain
Keywords: Communication networks, Optimization algorithms, Ant colony optimization algorithm, Terminal
assignment problem.
Abstract: The past two decades have witnessed tremendous research activities in optimization methods for
communication networks. One important problem in communication networks is the Terminal Assignment
Problem. This problem involves determining minimum cost links to form a network by connecting a
collection of terminals to a collection of concentrators. In this paper, we propose a Hybrid Ant Colony
Optimization Algorithm to solve the Terminal Assignment Problem. We compare our results with the
results obtained by the standard Genetic Algorithm, the Tabu Search Algorithm and the Hybrid Differential
Evolution Algorithm, used in literature.
1 INTRODUCTION
In the last decades the literature on
telecommunication network problems has grown
explosively. This is mainly due to the dramatic
growth in the use of the Internet (Salcedo-Sanz and
Yao, 2004; Yao et al. 2005). Terminal assignment
(TA) is an important issue in telecommunication
networks optimization.
The target of the TA problem implies fixing the
minimum cost links to form a network between a
specified set of terminals and concentrators (Khuri
and Chiu, 1997). The objective is to connect
terminals to concentrators under three constraints:
1. each terminal is assigned to one (and only
one) concentrator;
2. the total number of terminals assigned to
any concentrator does not overload that
concentrator, i.e. is within the concentrators
capacity and,
3. balanced distribution of terminals among
concentrators.
Under these constraints, an assignment with the
lowest possible cost is sought.
The TA problem is a NP-complete combinatorial
optimization problem (Salcedo-Sanz and Yao,
2004). This means that the time required to solve the
problem increases very quickly as the size of the
problem grows. The intractability of this problem is
a motivation for the pursuits of a metaheuristic that
produce approximate, rather than exact, solutions. In
(Dorigo, 1991; Dorigo et al. 1991; Dorigo et al.
1996) the use of an Ant Colony Optimization
algorithm as a new metaheuristic was proposed in
order to solve combinatorial optimization problems.
An Ant Colony Optimization algorithm (ACO) is
essentially a system based on agents which simulate
the natural behavior of ants, including mechanisms
of cooperation and adaptation. This new
metaheuristic has been shown to be both robust and
versatile. The ACO algorithm has been successfully
applied to a range of different combinatorial
optimization problems (ACO HomePage).
In this paper we present a Hybrid Ant Colony
Optimization (HACO) algorithm coupled with a
local search, applied to the TA problem. Our
algorithm is based on the HACO algorithm proposed
by Gambardella et al. (1999) for solving the
quadratic assignment problem. The HACO uses
pheromone trail information to perform
modifications on TA solutions, unlike more
traditional ant systems that use pheromone trail
144
Moreira Bernardino E., Moreira Bernardino A., Manuel Sánchez-Pérez J., Antonio Gomez Pulido J. and Ángel Vega-Rodríguez M. (2009).
A HYBRID ANT COLONY OPTIMIZATION ALGORITHM FOR SOLVING THE TERMINAL ASSIGNMENT PROBLEM.
In Proceedings of the International Joint Conference on Computational Intelligence, pages 144-151
DOI: 10.5220/0002322001440151
Copyright
c
SciTePress

information to construct complete solutions. The
HACO uses also a diversification mechanism that
periodically reinitializes all the pheromone trails.
We compare the performance of HACO with
three algorithms: Genetic Algorithm (GA), Tabu
Search (TS) Algorithm, Hybrid Differential
Evolution (HDE) Algorithm, used in literature.
The paper is structured as follows. In Section 2
we describe the TA problem; in Section 3 we
describe the implemented HACO algorithm; in
Section 4 we present the studied examples; in
Section 5 we discuss the computational results
obtained and, finally, in Section 6 we report about
the conclusions.
2 TA PROBLEM
The TA Problem can be described as follows:
1. a set N of n distinct terminals;
2. a set M of m distinct concentrators;
3. a vector C, with the capacity required for
each concentrator (each concentrator is
limited in the amount of traffic that it can
accommodate);
4. a vector T, with the capacity required for
each terminal (the capacity requirement of
each terminal is known and may vary from
one terminal to another). The capacities are
positive integers and Ti is smaller or equal
to min (Ci…Cn);
5. a matrix CP, with the location (x,y) of
each concentrator (the concentrators sites
have fixed and known locations). The M
concentrators are placed on the Euclidean
grid.
6. a matrix CT, with the location (x,y) of
each terminal (the terminals sites have fixed
and known locations). The N terminals are
placed on the Euclidean grid.
The first objective is to assign each terminal to
one node of the set of concentrators, in such a way
that no concentrator oversteps its capacity. The
second objective is to minimize the distances
between concentrators and terminals assigned to
them. Finally, the third objective is to ensure a
balanced distribution of terminals among
concentrators.
Figure 1 illustrates an assignment to a problem with
N = 10 terminal sites and M = 3 concentrator
sites. The figure shows the coordinates for the
concentrators, terminal sites and also their
capacities.
Figure 1: TA Problem - Example.
3 PROPOSED HACO
ACO is a population-based optimization method for
solving hard combinatorial optimization problems.
ACO is based on the indirect communication of a
colony of simple agents, called (artificial) ants,
mediated by (artificial) pheromone trails. In ant
colony natural, ants indirectly communicate with
each other by depositing pheromone trails on the
ground and thereby influencing the decision
processes of other ants. This simple form of
communication between individual ants gives rise to
complex behaviours and capabilities of the colony as
a whole.
The first algorithm which can be classified
within this framework was presented by Dorigo,
Maniezzo and Colorni (1991, 1996), and Dorigo
(1991) and, since then, many diverse variants of the
basic principle have been reported in the literature.
The real ants behaviour is transposed into an
algorithm by making an analogy between:
1. real ants search - set of feasible solutions to
the problem;
2. amount of food in a source - fitness
function;
3. pheromone trail - adaptive memory.
In ant colony natural, while walking from food
sources to the nest or the nest to food sources, each
A HYBRID ANT COLONY OPTIMIZATION ALGORITHM FOR SOLVING THE TERMINAL ASSIGNMENT
PROBLEM
145

ant deposits a pheromone on the ground. All ants
can smell the pheromone while they walks.
Therefore, more pheromone on the path will
increase the probability of all ants to follow. In
short, the best paths will receive a greater deposit of
pheromones.
The pheromone trails in ACO serve as a
distributed, numerical information which the ants
use to probabilistically construct solutions to the
problem being solved and which the ants adapt
during the algorithm execution to reflect their search
experience.
The essential trait of ACO algorithms is the
combination of a priori information about the
structure of a promising solution with a posterior
information about the structure of previously
obtained good solutions.
Any high performing metaheuristic algorithm
has to achieve an appropriate balance between the
exploitation of the search experience gathered so far
and the exploration of unvisited or relatively
unexplored search space regions. In ACO several
ways exist of achieving such a balance, typically
through the management of the pheromone trails. In
fact, the pheromone trails induce a probability
distribution over the search space and determine
which parts of the search space are effectively
sampled. The management of pheromone trails is the
most important component of an ant system.
Exploration is a stochastic process in which the
choice of the component used to construct a solution
to the problem is made in a probabilistic way.
Exploitation chooses the component that maximises
a blend of pheromone trail values and partial
objective function evaluations.
The standard ACO algorithm uses pheromones
trail information to construct complete solutions.
Gambardella et al. (1999) in their paper present a
Hybrid Ant Colony System coupled with a local
search (HAS_QAP), applied to the quadratic
assignment problem (QAP). HAS-QAP uses
pheromone trail information to perform
modifications on QAP solutions. Our HACO
algorithm uses also pheromone trail information to
perform modifications on TA solutions, unlike
traditional ant systems that use pheromone trail
information to construct complete solutions.
In this paper we will also explore one of the most
successful emerging ideas combining local search
with a population based search algorithm. HACO
uses a modified ACO to explore several regions of
the search space and simultaneously incorporates a
mechanism (LS algorithm) to intensify the search
around some selected regions.
The first step for the HACO implementation
involves choosing a representation for the problem.
In this work, the solutions are represented using
integer vectors. We use the terminal-based
representation (Figure 2). Each position in the
vector corresponds to a terminal. The value carried
by position i of the chromosome specifies the
concentrator that terminal i is to be assigned to.
Figure 2: Terminal Based Representation.
For the TA, the set of pheromone trails is
maintained in a matrix T of size N*M, where the
entry T
ij
measures the desirability of assigning
terminal i to concentrator j.
The simplest way to exploit the ants search
experience is to make the pheromone update a
function of the solution quality achieved by each
particular ant. In HACO only the best solution found
during the search contributes to pheromone trail
updating (Gambardella et al. 1999). This makes the
search more aggressive and requires less time to
reach good solutions. Moreover, this has been
strengthened by an intensification mechanism. The
intensification mechanics is used to explore
neighbourhood more completely.
The algorithm uses also a diversification
mechanism after a pre-defined number of S
iterations without improving the best solution found
so far. Gambardella et al. (1999) have shown that
pheromone trail reinitialization, when combined
with appropriate choices for the pheromone trail
update can be very useful to refocus the search on a
different search space region and avoid the early
convergence of the algorithm.
HACO is based on the schematic algorithm of
Figure 3.
The main steps of HACO are the following:
Initialization of solutions – the initial solutions
can be created randomly or in a deterministic
form. The deterministic form is based in the
Greedy Algorithm proposed by Abuali et al.
(1994). This algorithm assigns terminals to the
closest feasible concentrator.
Evaluation of solutions – the fitness function is
responsible for performing this evaluation and
returning a positive number (fitness value)
that reflects how optimal the solution is. The
fitness function is based on the fitness
function used in (Salcedo-Sanz and Yao,
2004). The fitness function is based on: (1)
IJCCI 2009 - International Joint Conference on Computational Intelligence
146

the total number of terminals connected to
each concentrator (the objective is to
guarantee the balanced distribution of
terminals among concentrators); (2) the
distances between the concentrators and the
terminals assigned to them (the objective is to
minimize the distances between concentrators
and terminals assigned to them); (3) the
penalization if a solution is not feasible (the
objective is to penalize the solutions when the
total capacity of one or more concentrators is
overloaded). The objective is to minimize the
fitness function.
{
()
()
1
0,9 *
0
1
0,1*
,()
0
1
10
20* 1
0
500
1
1()
0
0
,()
M
fitness bal
c
c
N
dist
tct
t
Penalization
N
if total round
c
M
bal
c
N
abs round total
c
M
if Feasible
Penalization
N
if c t c
total
c
t
dist
tct
−
=+
∑
=
−
+
∑
=
⎧
⎛⎞
⎛⎞
=+
⎪
⎜⎟
⎜⎟
⎪
⎝⎠
⎝⎠
=
⎨
⎛⎞
⎛⎞
⎪
+−
⎜⎟
⎜⎟
⎪
⎝⎠
⎝⎠
⎩
=
−
=
⎧
=
∑
⎨
⎩
=
[] []
()
[] []
()
2
(). .
2
(). .
CP c t x CT t x
CP c t y CT t y
−+
=
−
Pheromone trail initialization – all pheromone
trails T
ij
are set to the same value
T
0
=1/(Q*f(X*)) (Gambardella et al.
1999). X* is the best solution found so far and
Q a parameter.
Modification of solutions – it consists in
repeating R modifications. A modification
consists on assigning a terminal t to a
concentrator c. First a terminal t is randomly
chosen (between 1 and N) and after a
concentrator c is chosen. A random number x
is generated between 0 and 1. If x is smaller
than q (parameter), the best concentrator c is
chosen in such a way that Ttc is maximum.
This policy consists in exploiting the
pheromone trail. If x is higher than q the
concentrator c is chosen with a probability
proportional to the values contained in the
pheromone trail. This consists in exploring the
solution space.
Local Search – the LS algorithm consists on
applying a partial neighbourhood examination.
We generate a neighbour by swapping two
terminals between two concentrators C1 and
C2 (randomly chosen). If isn’t find a better
solution then is created another set of
neighbours. In this case, one neighbour
results of assign one terminal of C1 to C2 or
C2 to C1. The neighbourhood size is
N(C1)*N(C2) or N(C1)*N(C2) +
N(C1)+N(C2). The LS algorithm consists
on the following steps:
C1 = random (number of concentrators)
C2 = random (number of concentrators)
NN = neighbours of ACTUAL-SOL (one
neighbour results of interchange one
terminal of C1 or C2 with one terminal
of C2 or C1)
SOLUTION = FindBest (NN)
If ACTUAL-SOL is best than SOLUTION
NN = neighbours of ACTUAL-SOL (one
neighbour results of assign one
terminal of C1 to C2 or C2 to C1)
SOLUTION = FindBest (NN)
If SOLUTION is best than ACTUAL-SOL
ACTUAL-SOL = SOLUTION
Else
ACTUAL-SOL = SOLUTION
Intensification – the intensification mechanism
permits to explore the neighbourhood more
completely and permits to return to previous
best solutions. If the intensification is active
and the solution X in the beginning of the
iteration is better, the ant comes back to the
initial solution X. The intensification is
activated when the best solution found so far
has been improved and remains active while at
least one ant succeeds on improving its
solution during the iteration.
Pheromone trail update – to speed-up the
convergence the pheromone trails are updated
by taking into account only the best solution
found so far (Gambardella et al. 1999). The
pheromone trails are updating by setting:
T
ij
=(1-x1)*T
ij
, where 0<x1<1 is a
parameter that controls the evaporation of the
pheromone trail
T
iXi
*=T
iXi
*+x2/f*(X*), where 0<x2<1
is a parameter that controls the influence of
the best solution X* in the pheromone trail.
Diversification – this mechanism restarts the
pheromone trails and creates new solutions for
each ant. We kept for the following iteration
the best solution found so far.
More information about ACO can be found in
(ACO HomePage).
(
1
)
(
2
)
(3)
c(t)= concentrator of terminal t
t = terminal c = concentrator
M = number of concentrators N = number of terminals
A HYBRID ANT COLONY OPTIMIZATION ALGORITHM FOR SOLVING THE TERMINAL ASSIGNMENT
PROBLEM
147

Figure 3: HACO Algorithm.
4 EXAMPLES
In order to test the performance of our approach, we
use a collection of TA instances of different sizes.
We take 9 problems from literature (Bernardino et
al. 2008).
Table 1 presents the 9 problems that were used to
test our algorithm.
Table 1: TA Instances.
Problem N M Total T Total C
1 10 3 35 39
2 20 6 55 81
3 30 10 89 124
4 40 13 147 169
5 50 16 161 207
6 50 16 173 208
7 70 21 220 271
8 100 30 329 517
9 100 30 362 518
5 RESULTS
To compare our results we consider the results
produced with the classical Genetic Algorithm, the
Tabu Search Algorithm and the Hybrid Differential
Evolution Algorithm. The GA was first applied to
TA by Abuali et al. (1994). The GA is widely used
in literature to make comparisons with other
algorithms. The GA adopted uses “one-point”
method for recombination, “change order” method
for mutation and tournament method for selection.
In “change order”, two genes are randomly selected
and exchanged. TS was applied to this problem by
Xu et al. (2004) and Bernardino et al. (2008). We
compare our algorithm with the TS algorithm
proposed by Bernardino et al. (2008). HDE was
applied to this problem by Bernardino et al. ( 2009).
Table 2 presents the best-obtained results with
HACO, GA, TS and HDE. The first column
represents the problem number (Prob) and the
remaining columns show the results obtained
(Fitness, Time – Run Times) by the four algorithms.
The algorithms have been executed using a
processor Intel Core Duo T2300.
The HDE and GA were applied to populations of
200 individuals. The initial solutions were created
using the Greedy Algorithm.
The run time corresponds to the average time
that the algorithms need to obtain the best feasible
solution.
The values presented have been computed based
on 100 different executions for each test instance.
The four algorithms reach feasible solutions for
all test instances. In comparison, the HACO obtains
better solutions for larger instances. The TS is the
faster algorithm because can find good solutions in a
better running time. In HDE the crossover
probability is applied to each gene, generating
several perturbations by generation, for which the
algorithm slows down. Besides, in HDE is necessary
to carry out a concentrator conversion so that the
concentrator obtained stays always inside of the
defined range.
The better results obtained with HACO use R
between N/20 and N/3, x1>0.4 and x2>0.4
(Figure 4), Q=100, S between N*2 and N*4,
q>0.4 (Figure 4) and Number of ants ={30,40}.
These parameters were experimentally found to be
good and robust for the problems tested.
In our experiments we use a growing number of
ants. The number of ants was set to {10, 20,
30, 40, 50, 60, 70, 80, 90, 100}. We
studied the impact on the execution time, the
average fitness and the number of best solutions
IJCCI 2009 - International Joint Conference on Computational Intelligence
148
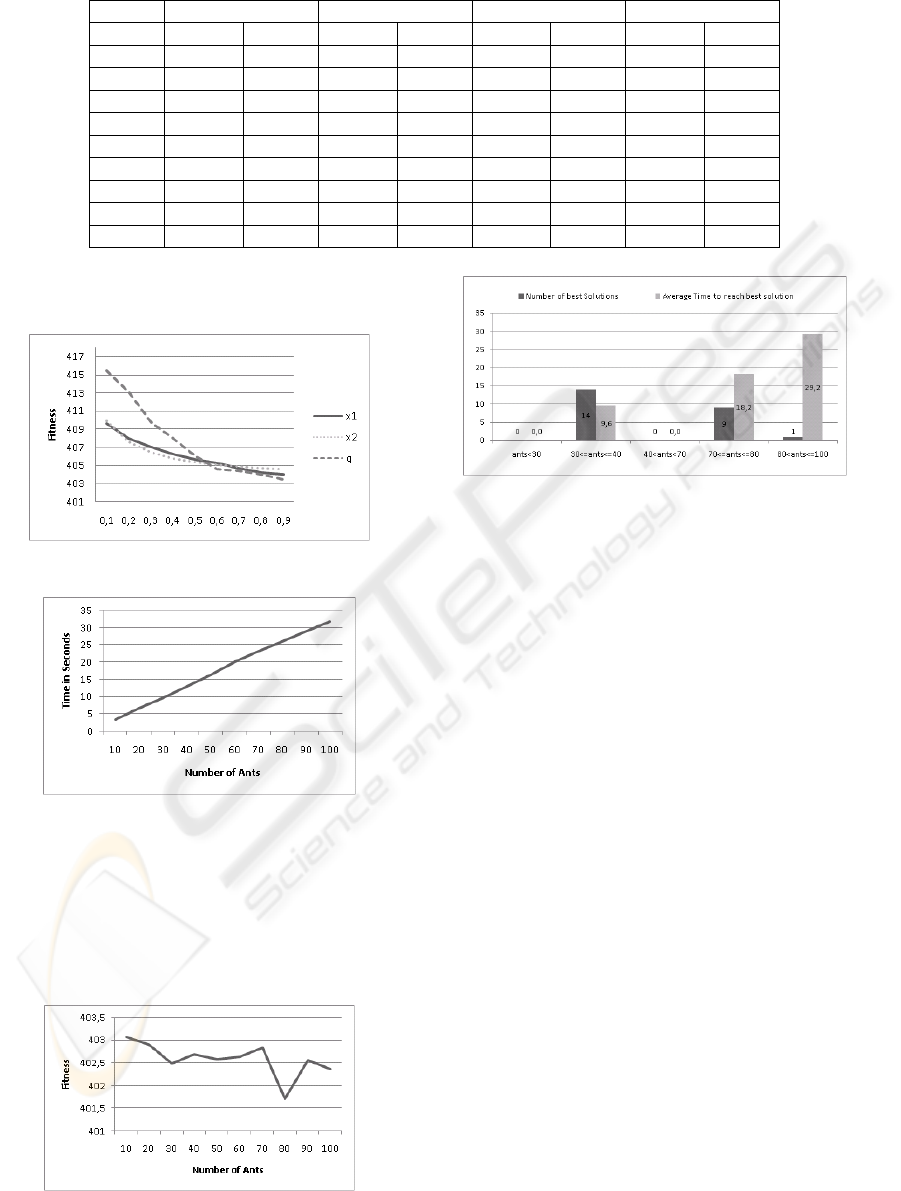
Table 2: TA Instances.
Prob GA Tabu Search HDE HACO
Fitness Time Fitness Time Fitness Time Fitness Time
1 65,63 <1s 65,63 <1s 65,63 <1s 65,63 <1s
2 134,65 <1s 134,65 <1s 134.65 <1s 134.65 <1s
3 284,07 <1s 270,26 <1s 270,26 <5s 270,26 <1s
4 286,89 <1s 286,89 <1s 286,89 <5s 286,89 <1s
5 335,09 <1s 335,09 <1s 335.09 <5s 335.09 2s
6 371,48 1s 371,12 <1s 371,12 58s 371,12 3s
7 401,45 2s 401,49 1s 401,21 118s 401,21 4s
8 563,75 4s 563,34 1s 563,19 274s 563,19 14s
9 703,78 5s 642,86 2s 642,83 456s 642,83 25s
found. A higher number of ants significantly
increase algorithm execution time (Figure 5).
Figure 4: Influence of parameters – Problem 7.
Figure 5: Number of Ants – Execution Time – Problem 7.
The results show that the best values are 30 and
40. With these values the algorithm can reach in a
reasonable amount of time a higher number of best
solutions (Figure 7). With a higher number of ants
the algorithm can reach a better average fitness
(Figure 6) but it needs much more time.
Figure 6: Number of Ants – Average Fitness – Problem 7.
Figure 7: Number of Ants – Number of Best Solutions –
Problem 7.
We also observe that a small number of ants
allows an initial faster convergence, but a worse
final result, following to an increased amount of
suboptima values (Figure 8). This can be explained
because the quality of the initial best-located
solution previous to the first restart, depends highly
on the population size: they need more population
diversity – it depends on the population size – to
avoid premature stagnation.
For parameter R, the number of swaps executed
using pheromone trail information, R between
[N/20...N/3] has been shown experimentally to
be more efficient (Figure 9). In our experiments R
was set to {0, 1, 2, …, N}.
In case of a high R the resulting permutation
tends to be too close to the best solution used to
perform global pheromone trail updating, which
makes it more difficult to generate new improving
solutions. A high R has also a significant impact on
the execution time (Figure 10). On the contrary, a
small R did not allow the system to escape from
local minima because after the local search, the
resulting solution was in most cases the same as the
starting permutation.
For S<N*2 and S>N*4 phenomena of
stagnation and insufficient intensification have been
observed (Figure 11).
A HYBRID ANT COLONY OPTIMIZATION ALGORITHM FOR SOLVING THE TERMINAL ASSIGNMENT
PROBLEM
149
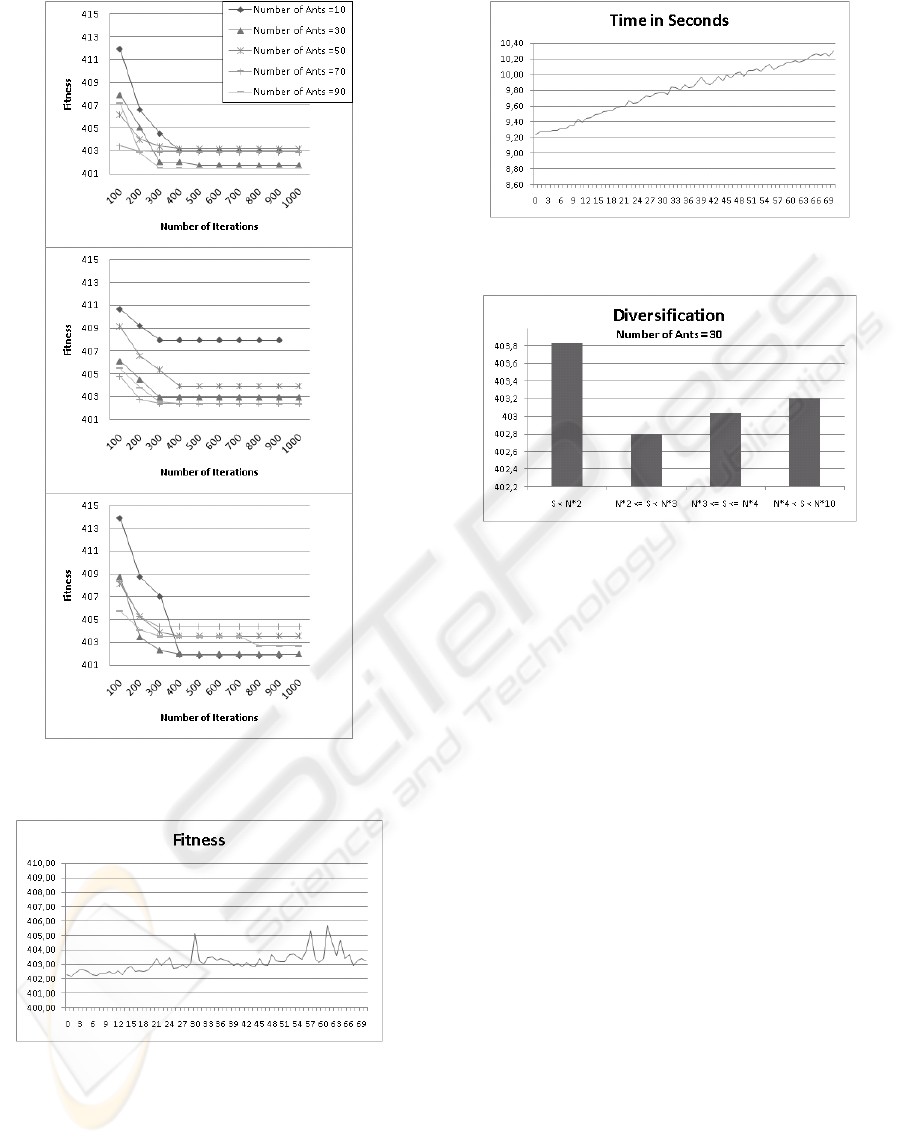
Figure 8: Number of Ants – Convergence – Three
different initial populations – Problem 7.
Figure 9: Number of modifications – Average Fitness –
Problem 7.
Large types of experiments and considerations
have been made to define other parameters.
In general, experiments have shown that the
proposed parameter setting is very robust to small
modifications.
Figure 10: Number of modifications – Execution Time –
Problem 7.
Figure 11: Diversification – Average Fitness – Problem 7.
6 CONCLUSIONS
In this paper we present a new Hybrid Ant Colony
Optimization Algorithm to solve the Terminal
Assignment Problem. The performance of' our
algorithm is compared with three algorithms: a
classical GA, a TS algorithm and a HDE algorithm.
Experimental results demonstrate that the
proposed HACO algorithm is an effective and
competitive approach in composing fairly
satisfactory results with respect to solution quality
and execution time for the Terminal Assignment
Problem.
The HACO presents better results for larger
problems. Our algorithm provides better solutions
with smaller fitness values for larger problems. The
TS is the faster algorithm.
In literature the application of HACO for this
problem is nonexistent, for that reason this article
shows its enforceability in the resolution of this
problem.
The implementation of parallel algorithms will
speed up the optimization process.
IJCCI 2009 - International Joint Conference on Computational Intelligence
150

REFERENCES
Abuali, F., Schoenefeld, D., Wainwright, R., 1994.
Terminal assignment in a Communications Network
Using Genetic Algorithms. In Proc. of the 22nd
Annual ACM Computer Science Conference, pp. 74–
81. ACM Press.
Ant Colony Optimization HomePage,
http://iridia.ulb.ac.be/dorigo/ACO/ACO.html
Bernardino, E., Bernardino, A., Sánchez-Pérez, J., Vega-
Rodríguez, M., Gómez-Pulido, J., 2008. Tabu Search
vs Hybrid Genetic Algorithm to solve the terminal
assignment problem. In IADIS International
Conference Applied Computing, pp. 404–409. IADIS
Press.
Bernardino, E., Bernardino, A., Sánchez-Pérez, J., Vega-
Rodríguez, M., Gómez-Pulido, J., 2009. A Hybrid
Differential Evolution Algorithm for solving the
Terminal assignment problem. In International
Symposium on Distributed Computing and Artificial
Intelligence 2009, pp. 178–185. Springer.
Dorigo, M., 1991. Ottimizzazione, apprendimento
automatico, ed algoritmi basati su metafora naturale
(Optimisation, learning and natural algorithms).
Doctoral dissertation, Dipartimento di Elettronica e
Informazione, Politecnico di Milano, Italy.
Dorigo, M., Maniezzo, V., Colorni, A. 1991. Positive
feedback as a search strategy. Technical Report 91-
016, Dipartimento di Elettronica e Informazione,
Politecnico di Milano, Italy.
Dorigo, M., Maniezzo, V., Colorni, A., 1996. The ant
system: Optimization by a colony of cooperating
agents. IEEE Transactions on Systems, Man, and
Cybernetics. 26, 29–41.
Gambardella, L. M., Taillard, E. D., and Dorigo, M., 1999
Ant colonies for the quadratic assignment problem.
Journal of the Operational Research Society, 50(2),
167-176.
Khuri, S., Chiu, T., 1997. Heuristic Algorithms for the
Terminal Assignment Problem. In Proc. of the ACM
Symposium on Applied Computing, pp. 247–251.
ACM Press.
Salcedo-Sanz, S., Yao, X., 2004. A hybrid Hopfield
network-genetic algorithm approach for the terminal
assignment problem. IEEE Transaction On Systems,
Man and Cybernetics, 2343–2353.
Xu, Y., Salcedo-Sanz, S., Yao, X. 2004 Non-standard cost
terminal assignment problems using tabu search
approach. In IEEE Conference in Evolutionary
Computation, vol. 2, pp. 2302–2306.
Yao, X., Wang, F., Padmanabhan, K., Salcedo-Sanz, S.,
2005. Hybrid evolutionary approaches to terminal
assignment in communications networks. In Recent
Advances in Memetic Algorithms and related search
technologies, vol. 166, pp. 129–159. Springer, Berlin.
A HYBRID ANT COLONY OPTIMIZATION ALGORITHM FOR SOLVING THE TERMINAL ASSIGNMENT
PROBLEM
151
