SOLVING THE NON-SPLIT WEIGHTED RING ARC-LOADING
PROBLEM IN A RESILIENT PACKET RING USING
PARTICLE SWARM OPTIMIZATION
Anabela Moreira Bernardino, Eugénia Moreira Bernardino
Department of Computer Science, School of Technology and Management, Polytechnic Institute of Leiria, Leiria, Portugal
Juan Manuel Sánchez-Pérez, Juan Antonio Gómez-Pulido, Miguel Angel Vega-Rodríguez
Dep. of Technologies of Computers and Communications, Polytechnic School, University of Extremadura, Cáceres, Spain
Keywords: Weighted ring Arc-Loading problem, Particle swarm optimization, Local search, Optimization.
Abstract: Massive growth of the Internet traffic in last decades has motivated the design of high-speed optical
networks. Resilient Packet Ring (RPR), also known as IEEE 802.17, is a standard designed for the
optimized transport of data traffic over optical fiber ring networks. Its design is to provide the resilience
found in SONET/SDH networks but instead of setting up circuit oriented connections, providing a packet
based transmission. This is to increase the efficiency of Ethernet and IP services. In this paper, a weighted
ring arc-loading problem (WRALP) is considered which arises in engineering and planning of the RPR
systems (combinatorial optimization NP- complete problem). Specifically, for a given set of non-split and
uni-directional point-to-point demands (weights), the objective is to find the routing for each demand (i.e.,
assignment of the demand to either clockwise or counter-clockwise ring) so that the maximum arc load is
minimized. This paper suggests four variants of Particle Swarm Optimization (PSO), combined with a Local
Search (LS) method to efficient non-split traffic loading on the RPR. Numerical simulation results show the
effectiveness and efficiency of the proposed methods.
1 INTRODUCTION
This paper concerns load balancing problems on
RPR, where the RPR is offered by IEEE 802.17
(RPR Alliance, 2004). The RPR is in essence, a
distributed Ethernet switch, in which the RPR nodes
are connected with two counter-rotating rings
(clockwise and counter-clockwise ring). The ring
spans are either SONET of Gbit Ethernet. The
(unidirectional) point-to-point traffic demands
(10/100/1000 Ethernet and/or TDM) can be carried
on either ring.
Given a network and a set D of communications
requests, a fundamental problem is to design a
transmission route (direct path) for each request such
that high load on the arcs/edges is avoided, where an
arc is an edge endowed with a direction. The load of
an arc is defined to be the total weight of those
requests that are routed through the arc in its
direction (WRALP) and the load of an edge is the
number of routes traversing the edge in either
direction (WRELP). In general each request is
associated with a non-negative integer weight.
Practically, the weight of a request can be
interpreted as a traffic demand or the size of the data
to be transmitted.
The load balancing problems can be classified
into two formulations: with demand splitting
(WRALP) or without demand splitting (non-split
WRALP). Split loading allows the splitting of a
demand into two portions to be carried out in two
directions, while a non-split loading is one in which
each demand must be entirely carried out in either
the clockwise or counter-clockwise direction. In
either split or non-split cases, WRELP/WRALP ask
for a routing scheme such that maximum load on
arcs/edges is minimized. In this paper we study the
WRALP without demand splitting.
For research on the no-split WRELP, Cosares
and Saniee (1994) and Dell’Amico et al. (1998)
studied the problem on SONET rings. Cosares and
Saniee (1994) proved that the formulation without
230
Moreira Bernardino A., Moreira Bernardino E., Manuel Sánchez-Pérez J., Antonio Gomez Pulido J. and Ángel Vega-Rodríguez M. (2009).
SOLVING THE NON-SPLIT WEIGHTED RING ARC-LOADING PROBLEM IN A RESILIENT PACKET RING USING PARTICLE SWARM OPTIMIZA-
TION.
In Proceedings of the International Joint Conference on Computational Intelligence, pages 230-236
DOI: 10.5220/0002322102300236
Copyright
c
 SciTePress

demand splitting is NP-complete. This means that
we cannot guarantee to find the best solution in a
reasonable amount of time. For the split problem,
various approaches are summarized by Schrijver et
al. (1998) and their algorithms compared in Myung
and Kim (2004) and Wang (2005).
The non-split WRALP considered in the present
paper is identical to the one described by Kubat and
Smith (2005) - non-split WRALP, Cho et al. (2005)
- non-split WRALP and WRALP and Yuan and
Zhou (2004) - WRALP. Their objective is to
produce feasible solutions in a reduce amount of
time (using algorithms that produce approximate
solutions). Our objective is to compare the
performance of our algorithms in achieving the
optimal solution. A heuristic method can greatly
improve the quality of a solution as the domain
knowledge is introduced, but this process will cost
much time.
In this article we report the results of the
application of four different variants of PSO, all of
them newer implementations to solve this problem
and we also present a novel binary local search PSO
(LS-PSO) to solve this problem.
The paper is structured as follows. In Section 2
we present the problem; in section 3 we describe the
algorithms implemented while in Section 4 we show
the studied examples; in Section 5 we discuss the
computational results obtained and, finally, in
Section 6 we report about the conclusions.
2 PROBLEM DEFINITION
To effectively use the RPR’s potential, namely
spatial reuse, statistical multiplexing and bi-
directionality, it is necessary to route the demands
efficiently. Given a set of point-to-point
unidirectional customer traffic demands of specified
bandwidth, the demands should be assigned to the
clockwise or to the counter-clockwise ring to yield
the best performance.
Let R
n
be a n-node bidirectional ring with nodes
{n
1
, n
2
, …, n
n
} labelled clockwise. Each edge
{e
k
, e
k+1
} of R
n
, 1≤ k ≤ n is taken as two arcs
with opposite directions, in which the data streams
can transmit in either direction.
),(),,(
11 kkkkkk
eeaeea
+
−
+
+
==
A communication request on R
n
is an ordered
pair (s, t) of distinct nodes, where s is the
source and t is the destination. We assume that data
can be transmitted clockwise or counter-clockwise
on the ring without splitting. We use P
+
(s, t) to
denote the directed (s, t) – path clockwise
around R
n,
and P
-
(s, t) the directed (s, t) –
path counter-clockwise around R
n
.
Often a request (s, t) is associated with an
integer weight w>=0; we denote this weighted
request by (s,t ; w). Let
D={(s
1
,t
1
;w
1
),(s
2
,t
2
;w
2
),...,(s
m
,t
m
;v
m
)}
be a set of integrally weighted requests on R
n
. For
each request/pair (s
i
, t
i
) we need to design a
directed path P
i
of R
n
from s
i
to t
i
. A collection
P = {P
i
: i= 1, 2, ..., m}
of such directed paths is called a routing for D.
In this work, the solutions are represented using
binary vectors. If a position has the value 1 the
demand flows by the clockwise direction, 0
otherwise (see Table 1).
Table 1: Chromosome representation.
Pair(s, t) Demand
1: (1, 2) Æ 15
2: (1, 3) Æ 3
3: (1, 4) Æ 6
4: (2, 3) Æ 15
5: (2, 4) Æ 6
6: (3, 4) Æ 14
n=numberNodes=4
m=numberPairs=6
15 C
3 CC
6 CC
15 C
6 CC
14 C
C - clockwise
CC – counter-clockwise
Representation (x)
Pair
1
Pair
2
Pair
3
Pair
4
Pair
5
Pair
6
1 0 0 1 0 1
We assume that weights cannot be split, that is,
for some integer xi =1, 1≤ i ≤ m, the total
amount of data is transmitted along P
+
(s, t);
x
i
=0, the total amount of data is transmitted along
P
-
(s, t). The vector
x=(x
1
, x
2
, …, x
m
)
determines a routing scheme for D.
The
WRALP is formulated as follows:
W
i
,…,w
m
Ædemands of the pairs (s
i
,t
i
),…,(s
m
,t
m
)
x
i
, …, x
m
= 0 Æ ),( tisiP
−
; 1 Æ ),( tisiP
+
(1)
Load on arcs:
L(x,
+
k
a
)=
∑
++
∈ ),(: tisiPai
k
wi
L(x,
−
k
a
)=
∑
−−
∈ ),(: tisiPai
k
wi
(2)
∀k=1,…,n; ∀i=1,…,m
(3)
Fitness Function:
max{max L(x,
+
k
a
),max L(x,
−
k
a
)}
(4)
Constraints (1) in conjunction with constraints
(3) state that each demand is routed in either
clockwise (C) or counter-clockwise (CC) direction.
SOLVING THE NON-SPLIT WEIGHTED RING ARC-LOADING PROBLEM IN A RESILIENT PACKET RING
USING PARTICLE SWARM OPTIMIZATION
231

For an arc, the load is the sum of w
k
for clockwise or
counter-clockwise between nodes e
k
and e
k+1
. The
objective is to minimize the maximum load on the
arcs of a ring (4).
3 PARTICLE SWARM
OPTIMIZATION
PSO is an intelligent optimization algorithm,
originally developed by Kennedy and Eberhart in
1995, inspired by the behaviour of bird flock's
looking for food (Kennedy and Eberhart, 1995,
1997). Like Genetic Algorithms (GA), PSO is a
population-based optimization algorithm.
The initial population (P) of particles can be
created randomly or in a deterministic form. The
deterministic form is based in a Greedy Algorithm
proposed by Bernardino et al. (2008). Initially a
deterministic strategy is followed and in a second
phase is used the PSO algorithm to optimize the
solution.
Procedure Greedy:
FOR each pair
Give a direction (C – 1, CC – 0)
pos = random (numberPairs)
FOR k=j=pos until j=numberPairs + pos
IF (j > numberPairs)
k=j- numberPairs
Change direction pair
k
IF fitnessNewSolution
k
<fitnessOldSolution
k
Replace the previous value of pair
k
k++
j++
Whether continuous or discrete, the original and
most essential idea of PSO is: difference in position
leads to velocity and velocity leads to search.
Supposing that the searching space is D-
dimensional and m particles form a swarm, each
particle is looked as a point in the D-dimensional
space, and the ith particle represents a D-
dimensional vector x
i
=(x
i1
, x
i2
,…, x
iD
).
According to the fitness value, the particle is
updated to move towards the better area by the
corresponding operators till the best point is found.
In the iterative process, each particle’s previous best
position is remembered and denoted p
i
=(p
i1
,
p
i2
,…, p
iD
), and the globally best position in the
whole swarm is recorded as pg=(pg
1
, pg
2
,…,
pg
D
). The ith particle’s “flying” velocity is also a
D-dimensional vector, represented as v
i
=(v
i1
,
v
i2
,…, v
iD
) (i= 1, 2,…, p). At each step,
the velocity of all particles is adjusted as a sum of its
local best value, global best value and its present
velocity, multiplied by the three constants W, C
1
and
C
2
respectively, shown in (5); the position of each
particle is also modified by adding its velocity to the
current position, see (6).
)(
)(
22
11
1
k
ij
k
gj
k
ij
k
ij
k
ij
k
ij
xprc
xprcvwv
−××+
−××+×=
+
(5)
k
ij
k
ij
k
ij
vxx +=
+1
(6)
In (5-6) k represents the iteration number; r1,
r2 are two random numbers selected from a uniform
distribution in [0.0, 1.0]; W is the inertia
weight. C
1
and C
2
are two constant numbers, which
are often called the acceleration coefficients.
The four PSO variants used to solve the WRALP
are extensions of the basic PSO and were used to
solve discrete binary problems. To improve the
performance of the PSO algorithms developed we
apply a separate local search (LS) process to refine
individuals.
The LS algorithm consists on the following
steps:
P1 = random (number of pairs)
P2 = random (number of pairs)
N = neighbourhoods of ACTUAL-SOLUTION (one
neighbourhood results of interchange the
direction of P1 and/or P2)
SOLUTION = FindBest (N)
If ACTUAL-SOLUTION is worst than SOLUTION
ACTUAL-SOLUTION = SOLUTION
The performance of the child vector and its
parent is compared and the better one is selected. If
the parent is better, it is retained in the population.
The algorithm continues until a certain number
of cycles defined by the user, have passed.
3.1 Discrete Binary Particle Swarm
Optimization
As the basic PSO operates in continuous and real
number space, it can’t be used to optimize the pure
discrete binary problem. To handle this problem,
Kennedy and Eberhart (1997) proposed a discrete
binary PSO (KBPSO) algorithm, where the particles
take the values of binary vectors of length p and the
velocity defined the probability of bit x
ij
to take the
value 1. KBPSO reserved the updating formula of
the velocity (see (5)) while velocity was constrained
to the interval [0.0, 1.0] by a limiting
transformation function, that is, the particle changes
its bit value by (7-8) in KBPSO:
)1/(1)(
ij
v
ij
evS
−
+=
(7)
IJCCI 2009 - International Joint Conference on Computational Intelligence
232

⎩
⎨
⎧
≤
=
otherwise
vSrandif
x
ij
ij
0
)(()1
(8)
where the value of rand() drawn from the interval
[0.0, 1.0] and the function S(v) is a sigmoid
limiting transformation.
3.2 Constriction Coefficient Particle
Swarm Optimization
The constriction coefficient (CBPSO) was
introduced by Clerc and Kennedy (2002) as an
outcome of a theoretical analysis of swarm
dynamics. Velocities are constricted, with the
following change in the velocity update:
))(
)((
22
11
1
k
ij
k
gj
k
ij
k
ij
k
ij
k
ij
xpr
xprvv
−××+
−××+×=
+
ϕ
ϕκ
(9)
where
κ
is the constriction factor determined from
the following two equations:
4;
21
>+=
ϕ
ϕ
ϕ
ϕ
(10)
ϕϕϕ
κ
42
2
2
−−−
=
(11)
It should be noted, however, that Clerc’s velocity
(9) is simply a special case of the original velocity
(5) where the constants W, C
1
and C
2
are chosen
according to (10) and (11).
3.3 Modified Discrete Binary
Particle Swarm Optimization
According to an information sharing mechanism of
PSO, a modified discrete PSO (MBPSO) was
proposed by Shen and Jiang (2004) as follows. The
velocity v
ij
of every individual is a random
number in the range of [0.0, 1.0]. The resulting
change in position is then defined by the following
rule:
(0 ( ) ( )
f
v then x new x old
ij ij ij
i α << =
(12)
(0 1 2(1 ) ( )
f
v then x new p
ij ij ij
i α << + =
(13)
(1 2 (1 ) 1 ( )
f
v then x new g
ij ij ij
i α +<< =
(14)
where α is a random value in the range of [0.0,
1.0] named static probability.
To circumvent convergence to local optima and
improve the ability of the modified PSO algorithm
to overcome local optima, five percent of particles
are randomly selected, and each site of the selected
particles has a probability of 0.5 to vary the value
in a stochastic manner.
Using a static probability that decreases and
some percent of randomly fling particles to
overcome local optima, the MBPSO remains having
satisfactory converging characteristics.
3.4 The Probability Binary Particle
Swarm Optimization
Wang et al. (2008) propose a novel probability
binary PSO (PBPSO). In PBPSO, a novel updating
strategy is adopted to update the swarm and search
the global solution. The variant equations (5) and (6)
are all reserved for iterative evolution in PBPSO,
and a different formula is used to determine a binary
bit px
ij
, which can be denoted as follows:
)/()()(
minmaxmin
RRRxxL
ijij
−
−
=
(15)
⎩
⎨
⎧
≤
=
otherwise
xLrandif
px
ij
ij
0
)(()1
(16)
where L(x) is a linear function, its output value
belongs to (0,1); rand() is a stochastic number
selected from a uniform distribution in [0.0,
1.0]; and [Rmax, Rmin] is a predefined range
for gaining the probability value with L(x)
function.
Compare to KBPSO, now the vector x
i
is a real
number vector rather than the binary vector. To
obtain a probability value distributed in [0.0,
1.0], is used the linear function L(x) to calculate
it, which determines px
i
to be 1 or 0. The binary
vector px
i
= (px
i1
, px
i2
… px
iD
) can be
worked out, and then we can apply this binary vector
into the combinatorial optimization problem.
4 STUDIED EXAMPLES
We evaluate the utility of the algorithms using
identical examples produced by Cho et al. (2005).
The studied examples arise by considering six
different ring sizes – 5, 10, 15, 20, 25 or 30 nodes. A
ring in a telecommunication network will typically
contain between 5 and 20 nodes. Thus, we consider
the 5, 10 and 15 node rings to be ordinary-sized
rings and the 20, 25 and 30 node rings to be
extremely large rings.
For convenience, they are labeled Cij, where
1<i<6 represents the ring size and 1<j<3
represents the demand case.
SOLVING THE NON-SPLIT WEIGHTED RING ARC-LOADING PROBLEM IN A RESILIENT PACKET RING
USING PARTICLE SWARM OPTIMIZATION
233

5 RESULTS
Since its conception, much work has been done to
understand and develop the ideal parameters for
PSO implementation. The goal was to develop an
algorithm with an optimal balance between global
exploration and exploitation of local maxima. One
of the first issues encountered during PSO
implementation was the ability to control the search
space explored by the swarm. Early work done by
the KBPSO developers (mostly trial and error)
suggested that the best choice for C
1
and C
2
is 2.0
for each (Eberhart and Shi, 2001). This essentially
became standard in the literature until recent results
called the values into question. Several values of
inertial weights have been suggested, attempting to
strike a balance between global exploration and local
exploitation. It was suggested varying the inertial
weight linearly from 0.9 to 0.4 over the course of
the run (Eberhart and Shi, 2001).
Parametric studies, using CBPSO have suggested
that the optimal choice for φ1 and φ2 is 2.8 and
1.3, respectively (Carlisle and Doizier, 2001).
Shen and Jiang (2004) consider α=0.5 when
using MBPSO. Static probability α normally starts
with a value of 0.5 and decreases to 0.33 when
the iteration terminates.
In the work of Wang et al. (2008) small values of
Rmax and Rmin are harmful to PBPSO as the
algorithm cannot perform meticulous search well,
and the optimization results are both poorest in the
executions made. The simulation results showed that
the Rmin=-50 and Rmax=50 may be encouraged
as PBPSO both achieving the best optimization
results. In our tests that is not the case (see Figure 1).
Population size is another parameter that needs a
careful selection. Large populations, while providing
the most thorough exploration of the solution space,
increase the cost of more fitness evaluations and
computation time. For the PSO, it has been found
that relatively small population sizes can sufficiently
explore a solution space while avoiding excessive
fitness evaluations. Parametric studies have found
that a population size of about 30 is optimal for
many problems (Carlisle and Doizier, 2001).
Obviously, the parameters of the PSO variants
will seriously affect the real optimization
performance (see Figure 1). To know the PSO
variants well, we study and test all the combination
parameters of the different variants. Previous works
have proven that the traditional values of parameters
in PSO can keep algorithm work well, but since this
problem has a different specificity we perform a new
parameter studying using the test instance C32 (see
table 2).
Table 2: Best combination parameters.
Problem Parameters
KBPSO
0.5<w<0.9 0.8<C1=C2≤2
Descend =
{true,false}
MBPSO
0.5<α<0.7 Descend = {true,false}
CBPSO
0.6<φ1<3.2 1.2<φ2<3.3
PBPSO
-1≤Rmin1≤-20 -1≤Rmax1≤20
With or without varying linearly the inertial
weight / α at the course of the run the results
produced are very similar. With 30 particles the
algorithms can reach in a reasonable amount of time
a high number of optimal solutions.
Table 3 presents the best obtained results. The
first column represents the problem number
(Problem), the second and the third columns show
the number of nodes (Nodes) and the number of
pairs (Pairs), the fourth column shows the minimum
fitness values obtained and finally the fifth column
shows the number of iterations used to test each
instance. The number of iterations was selected
based upon preliminary observation. The algorithms
have been implemented using C++ and were
executed using a processor Intel Core Duo (2.66
GHZ, Windows XP). The algorithms were tested
using randomly initial solutions and deterministic
initial solutions.
Table 3: Results.
Problem Nodes Pairs Optimal Fitness Number Iterations
C11 5 10 161 200
C12 5 8 116 100
C13 5 6 116 10
C21 10 45 525 250
C22 10 23 243 200
C23 10 12 141 200
C31 15 105 1574 300
C32 15 50 941 250
C33 15 25 563 200
C41 20 190 2581 1000
C42
20 93
1482 500
C43
20 40
612 250
C51
25 300
4265 1500
C52
25 150
2323 500
C53
25 61
912 300
C61
30 435
5762 2500
C62
30 201
2696 1000
C63
30 92
1453 500
Table 4 presents the best-obtained results. The
first column represents the problem number (Prob.)
and the remaining columns show the results obtained
(T – run time in seconds and I – number of
iterations). The run time corresponds to the average
IJCCI 2009 - International Joint Conference on Computational Intelligence
234

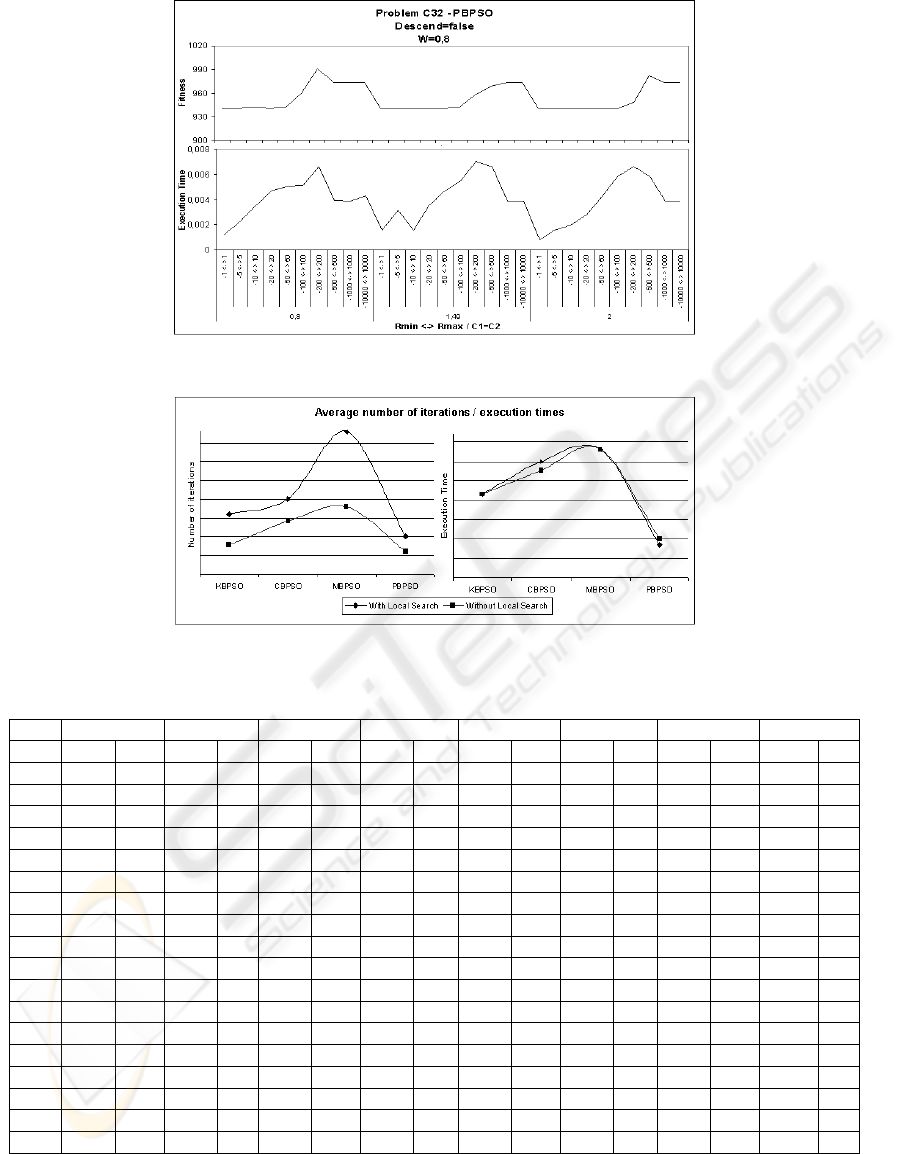
Figure 1: Problem C32 – Comparison between parameters.
Figure 2: Average number of iterations / execution times using the best parameters combination (only best solutions).
Table 4: Results – run times and number of iterations.
Prob. KBPSO LS-KBPSO CBPSO
LS- CBPSO
MBPSO LS-MBPSO
PBPSO LS-PBPSO
T I T I T I T I T I T I T I T I
C11
<0.001 <5 <0.001 <5 <0.001 <5 <0.001 <3 <0.001 <5 <0.001 <3 <0.001 <5 <0.001 <2
C12
<0.001 <5 <0.001 <3 <0.001 <5 <0.001 <3 <0.001 <5 <0.001 <3 <0.001 <5 <0.001 <2
C13
<0.001 1 <0.001 1 <0.001 1 <0.001 1 <0.001 1 <0.001 1 <0.001 1 <0.001 1
C21
<0.001
<15
<0.001
<15
<0.001
<20
<0.001
<20
<0.001
<60
<0.001 <20 <0.001
<15
<0.001
<15
C22
<0.001 <10 <0.001 <10 <0.001 <15 <0.001 <10 <0.001 <30 <0.001 <10 <0.001 <5 <0.001 <3
C23
<0.001 <5 <0.001 <3 <0.001 <5 <0.001 <3 <0.001 <10 <0.001 <3 <0.001 <5 <0.001 <3
C31
<0.3 <50 <0.3
<30
<0.3
<80
<0.3
<60
<0.3
<150
<0.3
<40
<0.2
<30
<0. 1
<20
C32
<0.001
<15
<0.001
<10
<0.001
<20
<0.001
<12
<0.001
<30
<0.001
<15
<0.001
<10
<0.001
<8
C33
<0.001
<12
<0.001
<5
<0.001
<12
<0.001
<5
<0.001
<15
<0.001
<10
<0.001
<10
<0.001
<5
C41
<1 <130 <0.5 <70 <1 <250 <1 <100
<1.5
<400 <0.5 <72 <0.5 <90 <0.1 <40
C42
<0.2 <45 <0.1 <20 <0.5 <110 <0.3 <40
<0.3
<150 <0.1 <30 <0.1 <40 <0.05 <20
C43
<0.001
<10
<0.001
<7
<0.001
<15
<0.001
<10
<0.001
<30
<0.001
<10
<0.001
<6
<0.001
<5
C51
<1 <350 <1.5 <150 <1.5 <600 <2 <200
<3
<750 <2 <140 <1 <500 <0.75 <70
C52
<0.5 <250 <0.2 <40 <0.3 <100 <0.4 <50
<0.5
<250 <0.3 <40 <0.1 <100 <0.1 <25
C53
<0.05 <40 <0.1 <25 <0.1 <70 <0.1 <30
<0.3
<150 <0.3 <20 <0.05 <40 <0,01 <15
C61
<4 <1200 <5 <250 <6 <1500 <6 <400 <7 <2000 <7 <300 <4 <1200 <2 <100
C62
<1.5 <200 <0.75 <60 <2 <250 <1.5 <100
<2
<400 <0.75 <60 <0.6 <400 <0.4 <40
C63
<0.2 <50 <0.2 <20 <0.1 <78 <0.15 <30 <0.3 <65 <0.15 <20 <0.1 <25 <0.075 <15
Aa
time that the algorithms need to obtain the best
solution. For each instance/variant, we perform 100
executions and the average computation time of the
algorithms is calculated using the 20 best results. For
the executions we use different seeds and we just
consider the best combination parameters. All the
algorithms reach the optimal solution.
SOLVING THE NON-SPLIT WEIGHTED RING ARC-LOADING PROBLEM IN A RESILIENT PACKET RING
USING PARTICLE SWARM OPTIMIZATION
235

In comparison, the LS-PSO obtains results in
smaller number of iterations. LS-PBSO is the faster
algorithm (see Figure 2). For large problems it
produces solutions with a smaller number of
iterations and in a smaller time. The main advantage
of including the LS algorithm is that it obtains
almost always a good solution with the correct
combination of parameters. In 100 executions with
the best combination parameters and the same
number of iterations it obtains a higher number of
optimal solutions as can be seen in Figure 3.
C32 - 100 iterations
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
KBPSO CBPSO MBPSO PBPSO
Without Local Search With Local Search
Figure 3: Problem C32 - Percentage of best solutions.
6 CONCLUSIONS
This paper proposes a novel LS algorithm combined
with four binary PSO variants to solve the WRALP.
The performance of all algorithms is compared.
The four PSO binary variants (with or without
LS algorithm) used to solve the WRALP prove to be
very effective in the resolution of the WRALP. LS-
PSO exhibits better optimization performance in
terms of speed and global search. LS-PBPSO variant
provides solutions in smaller number of iterations
and in a smaller execution time.
The continuation of this work will be the search
and implementation of new methods for speeding up
the optimization process.
REFERENCES
Bernardino, A.M., Bernardino, E.M., Sánchez-Pérez, J.M.,
Vega-Rodríguez, M.A., Gómez-Pulido, J.A., 2008.
Solving the Ring Loading Problem using Genetic
Algorithms with intelligent multiple operators. In
Proceedings of International Symposium on
Distributed Computing and Artificial Intelligence
2008 (DCAI 2008)
, pp. 235-244. Springer Berlin /
Heidelberg.
Carlisle, A., Doizier, G., 2001. An off- the-shelf PSO.
ProcWorkshop Particle Swarm Optimization,
Indianapolis, IN.
Cho, K.S., Joo, U.G., Lee, H.S., Kim, B.T., Lee, W.D.,
2005. Efficient Load Balancing Algorithms for a
Resilient Packet Ring. ETRI Journal, Vol.27, no.1, pp.
110-113.
Clerc, M., Kennedy, J., 2002. The particle swarm-
explosion, stability, and convergence in a
multidimensional complex space. IEEE transactions
on evolutionary computation
, Vol. 6, pp 58-64.
Cosares, S., Saniee, I., 1994. An optimization problem
related to balancing loads on SONET rings.
Telecommunication Systems, Vol. 3, No. 2, pp. 165-
181. Springer Netherlands.
Dell'Amico, M., Labbé, M., Maffioli, F., 1999. Exact
solution of the SONET Ring Loading Problem.
Operations Research Letters. Vol.25(3), pp. 119-129.
Eberhart, R.C., Shi, Y., 2001. Particle swarm
optimization: developments, applications and
resources. In
Proceedings 2001 Congress
Evolutionary Computation
, Vol.1. IEEE Press.
Kennedy, J., Eberhart, R., 1995. Particle swarm
optimization. In
Proceedings of IEEE International
Conference on Neural Networks
, pp. 1942-1948. IEEE
Press.
Kennedy, J., Eberhart, R., 1997. A discrete binary version
of the particle swarm algorithm. In
Proceedings of the
IEEE International Conference on Systems, Man and
Cybernetics
, pp. 4104-4108. IEEE Press.
Kubat, P., Smith, J.M., 2005. Balancing traffic flows in
resilient packet rings. Girard, André (ed.) et al.,
Performance evaluation and planning methods for the
next generation internet.
GERAD 25th Anniversary,
Series 6, pp. 125-140. Springer.
Myung, Y.S., Kim, H.G., 2004. On the ring loading
problem with demand splitting.
Operations Research
Letters
, Vol. 32, No. 2, pp. 167-173 (7), Elsevier.
RPR Alliance, 2004. A Summary and Overview of the
IEEE 802.17 Resilient Packet Ring Standard.
Schrijver, A., Seymour, P., Winkler, P., 1998. The ring
loading problem.
SIAM Journal of Discrete
Mathematics
, Vol. 11, pp. 1–14.
Shen, Q., Jiang, J.H., 2004. Modified Particle Swarm
Optimization Algorithm for Variable Selection in
MLR and PLS Modeling: QSAR Studies of
Antagonism of Angiotensin II Antagonists.
European
Journal of Pharmaceutical Sciences
, Amsterdam,
Netherlands, Vol. 22, pp. 145-152.
Wang, B.F., 2005. Linear time algorithms for the ring
loading problem with demand splitting.
Journal of
Algorithms
, Vol. 54, Issue 1, pp. 45-57. Academic
Press, Inc., Duluth, MN.
Wang, L., Wang, X., Fu, J., Zhen, L., 2008. A Novel
Probability Binary Particle Swarm Optimization
Algorithm and Its Application. Journal of software,
Vol. 3, N. 9.
Yuan J., Zhou S., 2004. Polynomial Time Solvability Of
The Weighted Ring Arc-Loading Problem With
Integer Splitting. Journal of Interconnection Networks,
Vol. 5(2), pp. 193-200.
IJCCI 2009 - International Joint Conference on Computational Intelligence
236