BI-OBJECTIVE OPTIMIZATION OF THE PLASMON-ASSISTED

LITHOGRAPHY

Design of Plasmonic Nanostructures

Caroline Prodhon

, Demetrio Mac´ıas

, Farouk Yalaoui

, Alexandre Vial

and Lionel Amodeo

Laboratoire d’Optimisation des Syst`emes Industriels, Institut Charles Delaunay

Laboratoire de Nanotechnologie et d’Instrumentation Optique, Institut Charles Delaunay

Universit´e de Technologie de Troyes, CNRS FRE 2848 - 12, rue Marie Curie, BP-2060 F-10010, Troyes Cedex, France

Keywords:

Bi-Objective Optimization, Evolutionary Strategy, Nanolithography.

Abstract:

We discuss the inﬂuence of the objective function within the context of plasmons-assisted lithography. From

previous publications, numerical experiments have shown that the maximization by means of an Evolutionary

Strategy of either the visibility or the contrast of the plasmons interference pattern related to the problem does

not lead to the ideal situation in which both criteria are maximal. The idea is then to tackle simultaneously

these two objective-functions. However, as they are strongly dependent, a more promising strategy is to focus

on the minimal and maximal near-ﬁeld scattered intensities involved in both previously studied criteria. We

think that an Evolutionary Strategy based on a bi-objective optimization of these new criteria will provide

more satisfactory solutions with respect to the physical constraints imposed.

1 INTRODUCTION

In the few past decades, an important amount of work

has been devoted to the application of Evolution-

ary Strategies (ES) for the solution of different kinds

of problems in several scientiﬁc disciplines (Djurisic

et al., 1997; Hodgson, 2000). The nanotechnologies,

a fairly new branch of physics, are not an exception

and reported results on the use of these methods is

becoming common (Herges et al., 2003; Kildishev

et al., 2007). One reason is that ES have proven suc-

cessful to solve problems on which classical methods

fail.

A particular application is for a little studied facet

of the inverse physic problem that consists in op-

timally synthesizing a nanostructure for plasmons-

assisted nanolithography. This optimization opens the

way to a more intelligent and systematic methodology

for the characterization of a nanostructureprior to fab-

rication. That is, it avoids the waste of time and ma-

terials that often results from the iterative adjustment

by trial and error of the experimental parameters. Al-

though this approach is commonly employed, there is

no guarantee of the optimality of the geometry of the

nanosturucture fabricated.

Encouraging results have been obtained thanks

to Evolutionary approaches. Nevertheless, the func-

tional form of the objective function and the deﬁnition

of the search space were not a sufﬁcient condition to

obtain a satisfactory physical solution, that in the con-

text of that application required the simultaneous ful-

ﬁllment of two apparently conﬂicting objectives. In

this paper, we further discuss this issue aiming to have

a better understanding on the inﬂuence of the deﬁni-

tion of the objective function on the solution of a real-

world optimization problem in near-ﬁeld physics.

In Section 2, we formulate the problem and brieﬂy

discuss the difﬁculties for its solution. Section 3 is

devoted to the choiceof the objective-functionand the

proposed idea based on bi-objective optimization for

the characterization of a nanostructure. We give our

main conclusions and ﬁnal remarks in Section 4.

2 SCATTERING OF LIGHT

We consider the scattering of light from a one-

dimensional multilayered geometry (see Fig.1).

The region x

+ ζ

) is a homogeneous

medium characterized by its refractive index n

. The

region

+ ζ

) > x

> −

+ ζ

) is ﬁlled with

a metal with complex frequency-dependent index of

306

Prodhon C., Macías D., Yalaoui F., Vial A. and Amodeo L. (2009).

BI-OBJECTIVE OPTIMIZATION OF THE PLASMON-ASSISTED LITHOGRAPHY - Design of Plasmonic Nanostructures.

In Proceedings of the International Joint Conference on Computational Intelligence, pages 306-309

DOI: 10.5220/0002322403060309

 SciTePress

refraction n

(ω). The upper and lower interfaces ,

) and ζ

), are assumed to be two arbitrarily

corrugated surfaces separated by a distance d, which

also is the mean thickness of the metallic ﬁlm. The

medium in the region x

< −

+ ζ

) is a homoge-

neous dielectric of constant refractive index n

. Al-

though in remainder of the presentation we have con-

sidered only three regions for this particular appli-

cation, this is not a restrictive condition. However,

as it will become evident in the following, a larger

number of interfaces would unnecesarily increase the

complexity of the direct scattering problem, without

contributing with additional information to the op-

erational principles of the optimization method em-

ployed here.

inc



= d/2 + ζ

)

= -d/2 + ζ

)

Figure 1: Geometry of the scattering problem.

The plane of incidence is the x

- plane. With ref-

erence to Fig. 1, the surface is illuminated from the

region x

+ ζ

) with a p- or s- polarized plane

wave. The single nonzero component of the electric

or magnetic vector of the incident ﬁeld has the form

|ω)

inc

= ψ

exp{i[kx

− α

(k)x

]}, (1)

where α

(k) =

(ω/c)

− k

, ω is the frequency of

the ﬁeld, and c is the speed of light in vacuum. A

time dependence of the form exp(−iωt) is assumed,

but explicit reference to it is suppressed.

As described by (Gu et al., 1993), the application of

Green’s Integral Theorem to each region in Fig. 1,

together with the respective boundary conditions for

each interface, lead to the following system of cou-

pled integral equations

(0)

|ω)θ(x

− (d/2 + ζ

))) = ψ

inc

|w) +

+ lim

ε→0

∞

−∞

′

(1)

′

|ω)H

(0)

′

)

− lim

ε→0

∞

−∞

′

(1)

′

|ω)L

(0)

′

)

, (2)

0 = lim

ε→0

4π

∞

−∞

′

(1)

′

|ω)H

(11)

′

)

− lim

ε→0

4π

∞

−∞

′



(ω)

(1)

′

|ω)L

(11)

′

)



− lim

ε→0

4π

∞

−∞

′

(2)

′

|ω)H

(12)

′

)

− lim

ε→0

4π

∞

−∞

′

(2)

′

|ω)L

(12)

′

)

, (3)

(2)

|ω) =

lim

ε→0

4π

∞

−∞

′

−ϕ

(1)

′

|ω)H

(21)

′

)

− lim

ε→0

4π

∞

−∞

′



(ω)

(1)

′

|ω)L

(21)

′

)



− lim

ε→0

4π

∞

−∞

′

(2)

′

|ω)H

(22)

′

)

− lim

ε→0

4π

∞

−∞

′

(2)

′

|ω)L

(22)

′

)

(4)

and

0 = lim

ε→0

4π

∞

−∞

′

(2)

′

|ω)H

(s)

′

)

− lim

ε→0

4π

∞

−∞

′



(ω)

(2)

′

|ω)L

(s)

′

)



, (5)

where ε

= n

, ε

(ω) = n

and ε

= n

. Also,

(1)

|ω), χ

(1)

|ω), ϕ

(2)

|ω) and χ

(2)

|ω) in

Equations (2), (3),(4) and (5), respectively, are known

as source functions and are given by

(1)

|ω) = ψ

(0)

|ω)



=d/2+ζ

)+ε

, (6)

(1)

|ω) =



−ζ

′

)

∂

∂x

∂

∂x



|ω)



=d/2+ζ

)+ε

(7)

(2)

|ω) = ψ

|ω)



=−d/2+ζ

)

, (8)

(2)

|ω) =



−ζ

′

)

∂

∂x

∂

∂x



|ω)



=−d/2+ζ

)

(9)

The source functions (6) and (7) are the ﬁeld and its

normal derivative evaluated on the interface d/2 +

BI-OBJECTIVE OPTIMIZATION OF THE PLASMON-ASSISTED LITHOGRAPHY - Design of Plasmonic

Nanostructures

307

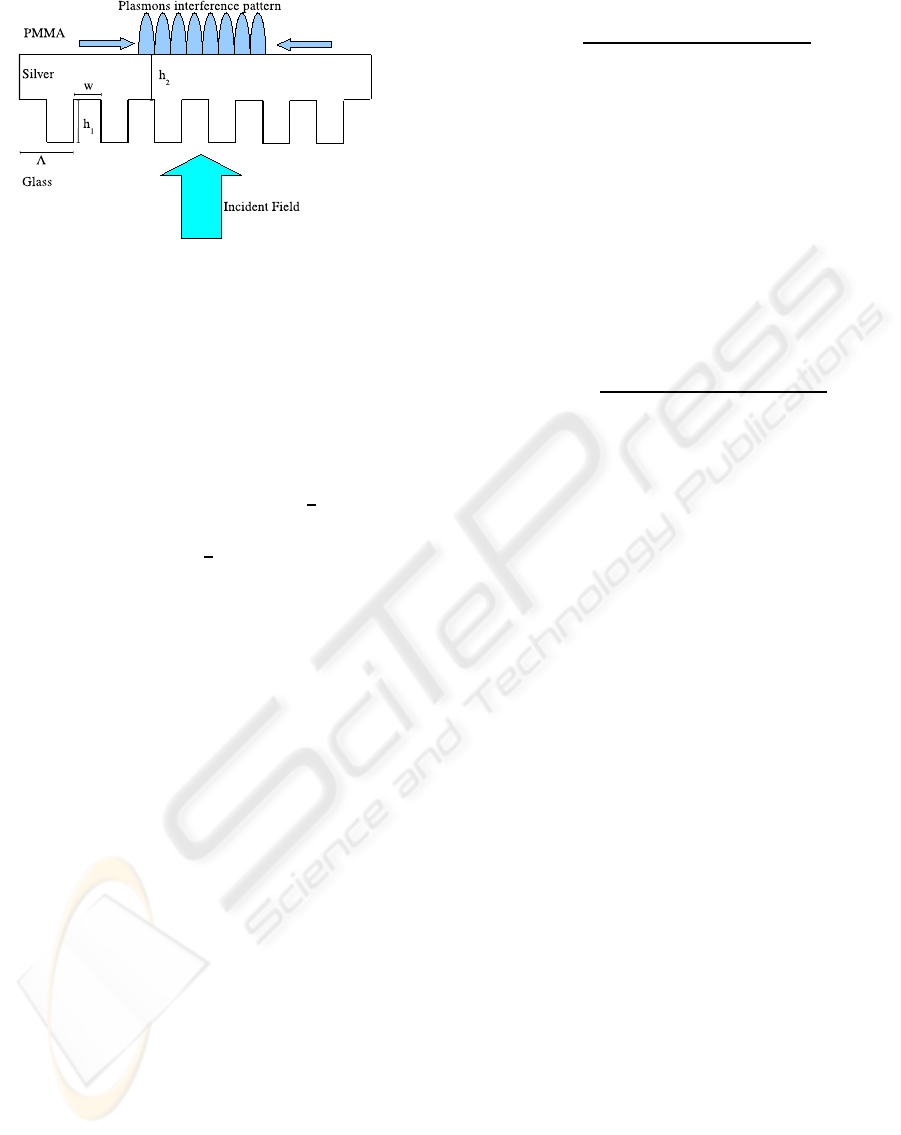
Figure 2: Surface-Plasmons Interference.

); whereas the source functions (8) and (9) cor-

respond to the ﬁeld and its normal derivative evalu-

ated on the surface −d/2+ζ

). The kernels of the

integral equations (2)-(5) are explicitly written in the

appendix A of (Gu et al., 1993).

Following them, the coupled integral equations (2)-

(5) are solved numerically to determine the source

functions (6)-(9), which are necessary to compute the

total ﬁeld ψ

(0)

|ω) in the region x

+ ζ

) or

the ﬁeld ψ

(2)

|ω) transmitted through the metallic

ﬁlm into the region x

< −

+ ζ

The total or transmitted intensities can be written as

the squared modulus of they respective ﬁelds, that is

(α)

|ω) = |ψ

(α)

|ω)|

, (10)

where α = 0,2

The formalism just described has been extensively

used for the solution of different kinds of problems in

near- and far-ﬁeld scattering and SERS (Sanchez-Gil

et al., 2002), or in Plasmonics (Giannini and Sanchez-

Gil, 2007). A particular application of this fairly new

branch of Nanosciences, that has attracted the atten-

tion of different research groups, is the Plasmons-

Interference-Assisted Nano-Lithography. As shown

by (Derouard et al., 2007), this technique offers the

possibility to conform the topography of a photosen-

sitive material through the interference of wave-like

solutions of Maxwell’s Equations called Plasmons.

This phenomenonis schematically described in Fig.2,

where as a consequence of the interaction bewteen the

squared grating and the incident ﬁeld, two counter-

propagating plasmons generate interference pattern

on the ﬂat interface of the metallic (silver) ﬁlm.

In addition to the experimental and numerical

evidence presented by (Derouard et al., 2007),

some efforts have been conducted to maximize the

visibility of the interference pattern depicted in

Fig.2, through the optimization of some geometrical

features of the nano-structure considered and the

illumination conditions. (Mac´ıas and Vial, 2008)

optimize the visibility

V(x

|p) =

(p)

|p)

max

− I

(p)

|p)

min

(p)

|p)

max

+ I

(p)

|p)

min

(11)

where the components of the vector p =

{θ

,w}

are the variables of interest. The

optimization of V(x

|p) provides feasible solutions

with high visibility. However, this approach presents

an important drawback as regards a weak contrast

C(x

|p) = I

(p)

|p)

max

− I

(p)

|p)

min

(12)

which implies that there will not be enough power

to modify the topography of the photo sensitive mate-

rial. Based on the fact that

V(x

|p) =

C(x

|p)

(p)

|p)

max

+ I

(p)

|p)

min

(Prodhon et al., 2009) propose to use C as objective

function. This provides better solutions in terms of

contrast, while keeping reasonable value of visibil-

ity. Furthermore, the objective-variables are closer to

the physical feasibility of the context of work. (Prod-

hon et al., 2009) conclude that the choice of criteria

ﬁtness function has signiﬁcant effects on the results.

Nevertheless, the ideal situation in which contrast and

visibility are maximal does not seem attainable when

these two objective functions are tackled separately.

Another drawback in the formulations of (Mac´ıas and

Vial, 2008) and (Prodhon et al., 2009) is that their

forward scattering solvers are based on the Finite-

Difference Time-Domain method (FDTD). Despite

its popularity, this approximative numerical method

presents important problems of numerical conver-

gence. Also, the accuracy of its results strongly de-

pends on the size of the elementary cell. For this

reason, in this work, we propose to use the rigorous

numerical integral method described in the previous

paragraphs for the computation of I

(α)

|ω).

3 OPTIMIZATION OF THE

INTERFERENCE PATTERN

An idea to achieve high quality solutions is to keep a

vision the more global as possible on the whole prob-

lem, i.e. to carry a search ensuring high values on

both C and V. Since C and V are strongly depen-

dent, a bi-objective optimization on these two crite-

ria may not be the best way to obtain the expected

results. A more promising strategy is to focus on

the near-ﬁeld scattered intensity involved in both pre-

vious studied criteria. Let I

(p)

|p)

max

= I

max

and

IJCCI 2009 - International Joint Conference on Computational Intelligence

308

(p)

|p)

min

= I

min

, a formulation of C as regard to

the maximum and minimum intensity is:

Max C(x

|p) ⇔ Max (I

max

− I

min

) (13)

⇔ Max(I

max

) and Min(I

min

)

(14)

The same transformation can be done on V.

Max V(x

|p) ⇔ Max (

max

− I

min

max

+ I

min

) (15)

⇔ Max

(

max

min

−

min

)

(

max

min

)

(16)

Let α =

max

min

Max V(x

|p) ⇔ Max(

α− 1

α+ 1

) (17)

⇔ Max(

α+ 1− 1

α+ 1

−

α+ 1

) (18)

⇔ Max(1−

α+ 1

) (19)

⇔ Max(α) (20)

⇔ Max(I

max

) and Min(I

min

)

(21)

Thus, from (14) and (21):

Max V(x

|p) ⇔ Max (I

max

) and Min (I

min

)

⇔ Max C(x

|p)

Even if physical limitations can reduce the ex-

pectancy of reaching both C ≈ 1 and V ≈ 1, this

relation shows that the previous optimization mod-

els were weak since a maximization on C should be

equivalent to a maximization on V (results not ob-

served until now). Furthermore, it is clear that both

max

and I

min

should be tackled in the process to

achieve good results. Thus a bi-objective approach

seems more promising. Note though that I

max

and

min

are linked by the electric ﬁeld scattered in the

near-ﬁeld of the surface. To handle the problem, we

propose to apply the Pareto Archived Evolutionary

Strategy (PAES). PAES is a multi-objective optimizer

which uses a simple local search evolution strategy.

It exploits an archive of non-dominated solutions to

estimate the quality of new candidate solutions. The

validation of this work is under process and should be

corroborated by the results from the experiments.

4 CONCLUSIONS

In this paper, we have discussed the inﬂuence of the

objective function within the context of plasmons-

assisted lithography. It has been shown that the max-

imization by means of an Evolutionary Strategy (ES)

of either the visibility or the contrast of the plasmons

interference pattern does not lead to the ideal situ-

ation in which both criteria are maximal. The idea

proposed to obtain more promising results is then to

tackle simultaneously two objective functions. How-

ever, since the contrast and the visibility are strongly

dependent but both involve the near-ﬁeld scattered in-

tensity, we propose to focus on the maximal and min-

imal values taken by this function. We suggest the

use of an ES based on a bi-objective optimization of

these new criteria to provide more satisfactory solu-

tions with respect to the physical constraints imposed.

REFERENCES

Derouard, M., Hazart, J., Lerondel, G., Bachelot, R., and

Royer, P.-M. A. P. (2007). Polarization-sensitive print-

ing of surface plasmon interferences. Opt. Express,

(15):4238–4246.

Djurisic, A., Elazar, J., and Rakic, A. (1997). Modeling the

optical constants of solids using genetic algorithms

with parameter space size adjustment. Opt. Comm.,

(134):407–414.

Giannini, V. and Sanchez-Gil, J. A. (2007). Calculations

of light scattering from isolated and interacting metal-

lic nanowires of arbitrary cross section by means of

green’s theorem surface integral equations in paramet-

ric form. J. Opt. Soc. Am. A, (24):2822–2830.

Gu, Z.-H., Lu, J. Q., and Maradudin, A. A. (1993). En-

hanced backscattering from a rough dielectric ﬁlm on

a glass substrate. J. Opt. Soc. Am. A, (10):1753–1764.

Herges, T., Schug, A., Merlitz, H., and Wenzel, W.

(2003). Stochastic optimization methods for structure

prediction of biomolecular nanoscale systems nan-

otechnology. Physical Chemistry Chemical Physics,

(14):1161–1167.

Hodgson, R. (2000). Genetic algorithm approach to particle

identiﬁcation by light scattering. Journal of Colloid

and Interface Science, (229):399–406.

Kildishev, A. V., Chettiar, U. K., Liu, Z., Shalaev, V. M.,

Kwon, D., Bayraktar, Z., and Werner, D. H. (2007).

Stochastic optimization of low-loss optical negative-

index metamaterial. J. Opt. Soc. Am. B, (24):A34–

A39.

Mac´ıas, D. and Vial, A. (2008). Optimal design of plas-

monic nanostructures for plasmon-interference as-

sisted lithography. Appl. Phys. B, (93):159–163.

Prodhon, C., Macias, D., Yalaoui, F., and Amodeo, A.

V. L. (2009). Evolutionary optimization for plasmon-

assisted lithography. In Springer-Verlag, editor, Ap-

plications of Evolutionary Computing, Evoworkshops,

volume 5484/2009.

Sanchez-Gil, J., Garcia-Ramos, J., and Mendez, E. R.

(2002). Electromagnetic mechanism in surface-

enhanced raman scattering from gaussian-correlated

randomly rough metal substrates. Opt. Express,

(10):879–886.

BI-OBJECTIVE OPTIMIZATION OF THE PLASMON-ASSISTED LITHOGRAPHY - Design of Plasmonic

Nanostructures

309