BRAIN CENTERS MODEL AND ITS APPLICATIONS TO EEG

ANALYSIS

Ivan Gorbunov

Psychology Department, State University, Saint-Petersburg, Russian Federation

Piotr Semenov

Technical Cybernetics Department, State Polytechnical University, Saint-Petersburg, Russian Federation

Keywords:

EEG, Neural networks, Back propagation, Human functional state identiﬁcation.

Abstract:

This paper presents a new approach to EEG analysis and human functional state discrimination. This is Brain

Centers Neural Network model (BCNN-model). We declare BCNN-model fundamentals and recent numerical

experiments results. These results approve that model has high accuracy in EEG reproduction and human state

discrimination. BCNN-model may have applications in functional state identiﬁcation and brain exploration.

1 INTRODUCTION

In this paper we present a new approach that can be

used in EEG analysis. Our main purpose is to create a

model that can represent EEG in a compact form and

can be good for brain exploration and human func-

tional state identiﬁcation (see section 3). We hope that

framework which we propose can be instrumental for

human functional state identiﬁcation via EEG analy-

sis. Data under considertion is an EEG time series -

EEG stored in a digital form. We use data of this kind

after some processing - digital ﬁltering and smooth-

ing - to train our model. We aim the model for repro-

duction of source time series. If this reproduction is

found accurate, then we can use synaptic weights of

the neural network with ﬁxed structure as a compact

presentation of a given functional state-speciﬁc EEG

State-of-the-art methods of the EEG analysis use

signal principal components separation techniques

(Ungureanu et al., 2004; Hyekyung and Seungjin,

2003) and methods of their sources localization in

brain (Zhukov et al., 2000; Koles, 1998). Visual-

ization of it permits brain functional diagnostics and

detection of different pathologies. However, discov-

ery of sources doesn’t assume an estimation of quan-

titative characteristics of interrelation between these

sources. And this makes such approach unstable po-

tentially because it considers the brain as a black box.

Also this makes the analysis of functional mecha-

nisms which are the foundation of many electrophys-

iological effects in brain more complex.

The proposed method gives us a capability to

qualitative assessing of physiological mechanisms

of psychological effects by discovery of interaction

structure between brain centers in model.

2 BCNN-MODEL

Our model is a four-layer feed-forward neural net-

work (Haykin, 1998) with modiﬁed back propagation

training procedure. This modiﬁcation requires that

some neurons have constant synaptic weights during

training. Figure 1 shows BCNN-model. We assume

Figure 1: feed-forward neural network in BCNN-model (I -

input, H - hidden, O - output)

that electric potentials, which are captured by elec-

trodes, are result of an interaction between brain cen-

ters. The network represents this. Informally, input

480

Gorbunov I. and Semenov P. (2009).

BRAIN CENTERS MODEL AND ITS APPLICATIONS TO EEG ANALYSIS.

In Proceedings of the International Joint Conference on Computational Intelligence, pages 480-483

DOI: 10.5220/0002322704800483

 SciTePress

and output layers represent the electrodes that regis-

ter the EEG time series. And two hidden layers repre-

sent the brain centers with some interaction structure

between them that is expressed by synaptic weights

between these layers. We consider that just this inter-

action schema generates electric potentials which are

registered on the scalp. Now, let’s describe each layer

in detail.

Network input layer has m neurons, where m is

number of EEG channels in the model. Synaptic

weights vector of each neuron from this layer are

constant (red links at the Figure 1) during network

training. For example, it is (0, 0, . . . , 0, 1, 0)

for

(m − 1)-th input neuron and m-th neuron activation

corresponds to m-th channel electrode potential. First

and second network hidden layers have n neurons

each, where n is the number of brain centers in the

model. So, each brain center corresponds to two neu-

rons from two hidden layers in the model. Synap-

tic weights of neurons from the second hidden layer

are also constant. We can interpret this as feedback

from output electric potentials to brain centers. On

the other hand it is necessary to have such network

structure to train network so it could reproduce initial

EEG. Second hidden layer has also n neurons. And its

synaptic weights are changing during training phase.

In particular both hidden layers present interaction be-

tween brain centers. So we interpret hidden layers

as brain centers with activating or inhibiting connec-

tions. And we aim for obtaining this internal interac-

tion schema via training synaptic weights of the sec-

ond hidden layer. Finally, the network’s output layer

has m neurons as its input layer. Outputs are electric

potentials being registered on the scalp by electrodes.

For simplicity we consider the output neurons as the

electrodes. Output layer’s synaptic weights are also

constant and equal to synaptic weights of the ﬁrst hid-

den layer. Thus interaction between brain centers and

electrodes is symmetrical. So we have the following

model of electric potential generating process: being

in some initial state, brain centers - 2-d and 3-rd net-

work layers - respond to input activation, conﬁgure

their internal connections and reproduce the appropri-

ate EEG signal. We assume that i-th brain center has

inﬂuence on j-th electrode that is inverse-proportional

to the square of the distance between them:

φ(i, j) ∼

(i, j)

(1)

ρ(i, j) is the speciﬁed distance that is represented by

the ﬁxed synaptic weight of any neuron in ﬁrst hid-

den and output layers. One should note that a certain

choice of proportionality coefﬁcient can badly affect

generalization capability of the neural network. Also

the choice of brain centers coordinates is the corner

stone of our BCNN-model. In our experiments we use

a linear independent matrix of second hidden layer’s

synaptic weights.

The BCNN-model is supposed to be trained by

time series that are EEG samples from electrodes. In

the BCNN-model the number of input layer neurons

is equal to the number of electrodes and correspond-

ing EEG channels. So as stated above we have one-

to-one correspondence between i-th input and output

neurons and i-th electrode. The main goal of the

training phase is to obtain such brain centers inter-

action weights so they make the tuned model suit-

able for EEG reproduction. We use a modiﬁcation of

the error back propagation method (Haykin, 1998) as

the training method. Here some synaptic weights are

being kept constant during network training and the

error back propagation process varies only synaptic

weights between hidden layers. To specify the model

in full we say that each neuron activation function is

a bipolar sigmoid due to its symmetry. Normalization

of input vector is done by the following simple linear

transformation:

t(x) =

max

− x

min

· (x − x

min

) − 1.0 (2)

−1

(y) =

(y + 1.0) · (x

max

− x

min

)

+ x

min

(3)

During the learning phase we use following instruc-

tions. Starting with any initial input vector we aim

to obtain the vector of ﬁrst samples of EEG time se-

ries array. After one pass through the network by the

modiﬁed error back propagation method we proceed

to using the vector with ﬁrst EEG samples as the in-

put. At this point we specify as ideal output a vector

that consists of second samples and so on. After one

learning epoch (one pass through all EEG time series

samples) is over we start it again.

3 EXPERIMENTS

We used the following data for our ﬁrst experiments:

an EEG of a person whose eyes were open (“Opened

Eyes”), an EEG of a person whose eyes were closed

(“Closed Eyes”) and an EEG of a person that was

watching fractal pictures (“Fractals”). These EEG

recordings were taken from sixteen electrodes and

were 17 seconds long each. The sampling rate in

analogue-digital conversion was 250 measurements

per second. EEG recording were preprocessed in the

following way: artifacts were deleted and then a band-

pass ﬁlter (1-70 Hz), a notch ﬁlter (50 Hz) and reason-

able smoothing were applied. The experiment was set

up in the following way. We set bipolar sigmoid pa-

rameter to value 0.2 and learning rate to value 1.5.

BRAIN CENTERS MODEL AND ITS APPLICATIONS TO EEG ANALYSIS

481

The learning procedure started with a random input

vector that was the same for all experiments. For each

experiment we ran 100 learning epochs. We used

16 EEG channels and 7 brain centers in the model.

To provide stationary of a human functional state we

used only ﬁrst 3 seconds of each EEG. As stated

above, we used in this study a linear independent ma-

trix with constant synaptic weights. Other weights

were chosen randomly but were the same in all exper-

iments. For this setup we obtained good results (see

table 1).

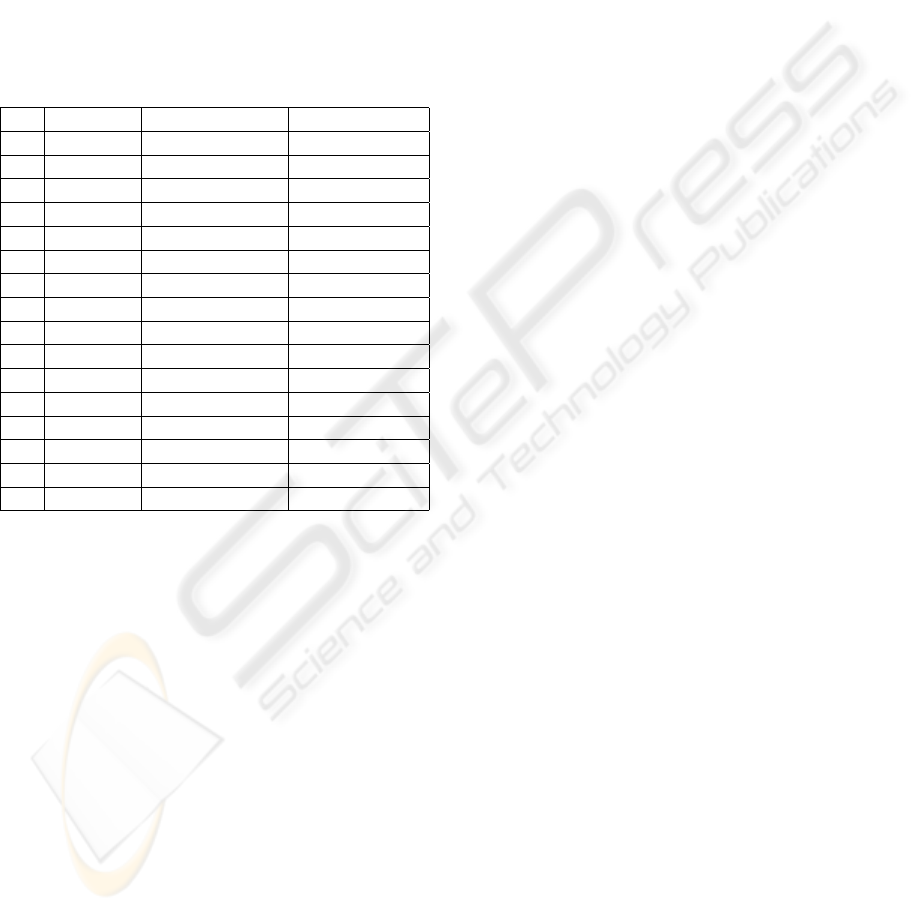
Table 1: Correlation between original EEG time series and

its reproduction by BCNN-model

“Fractal” “Opened Eyes” “Closed Eyes”

1 0.930 0.934 0.922

2 0.947 0.865 0.681

3 0.889 0.902 0.908

4 0.911 0.915 0.838

5 0.905 0.886 0.773

6 0.915 0.892 0.896

7 0.898 0.893 0.910

8 0.871 0.875 0.668

9 0.918 0.904 0.817

10 0.886 0.863 0.873

11 0.869 0.806 0.814

12 0.884 0.906 0.798

13 0.904 0.887 0.929

14 0.853 0.891 0.770

15 0.873 0.895 0.912

16 0.877 0.778 0.869

Table 1 shows a correlation between an origi-

nal EEG time series from different electrodes and

its reproduction by BCNN-model for “fractal” data,

“opened eyes” data and “closed eyes” data. One can

see that model provides high accuracy in reproduc-

tion of the EEG time series. Original sample data and

reproductions are shown on ﬁgures 3 and 4. So we

can conclude that BCNN-model is adequate for our

purposes. Now we can use brain centers interaction

schema weights as a compact numeric identiﬁcation

of a human functional state. For example let’s see ﬁg-

ure 2. It uses PCA (Principal Component Analysis)

(Jolliffe, 2002) visualization technique. Let’s con-

sider three clouds of points of different colors. They

present different data used in the training phase. Each

point corresponds to a single experiment where we

fetch only random 3 seconds from EEG. We see that

clouds are relatively compact in space but they in-

tersect and could not be separated by a linear func-

tion. On other hand we can see on the right plot of

ﬁgure 2 the PCA-visualization of the experimental

results based on ﬁrst three seconds of EEG record-

ing. Under these conditions (in the beginning of an

EEG recording) we can say about “cleanness” of hu-

man functional state. Using random 3 second cuts of

recordings in experiment is necessary for estimating

of model reliability for human functional state identi-

ﬁcation. To get discriminating rules for this identiﬁ-

cation we can use machine learning framework.

4 CONCLUSIONS

Despite of that point clouds in ﬁgure 2 are not linearly

separable, we can use SVM (Wang, 2005) technique

that is very popular in machine learning to provide ef-

fective human functional state identiﬁcation. We are

planning to use it in our further studies. Also we are

going to use these methods in medical applications,

where it is necessary to study pathological interac-

tions between brain centers. We are going to com-

pare results of our model with other methods of EEG

analysis and neuro-visualization (FMRI (Raichle and

Mintun, 2006) and PET (Phelps and Hoffman, 1975)).

At this point we can state that our BCNN-model has

many perspectives.

REFERENCES

Haykin, S. (1998). Neural Networks: A Comprehensive

Foundation. Prentice Hall, 2nd edition.

Hyekyung, L. and Seungjin, C. (2003). Pca+hmm+svm for

eeg pattern classiﬁcation. Proceedings of Seventh In-

ternational Symposium on Signal Processing and Its

Applications.

Jolliffe, I. (2002). Principal Component Analysis. Springer.

Koles, Z. (1998). Trends in eeg source localization. Elec-

troencephalography and Clinical Neurophysiology,

106:127–137.

Phelps, M. and Hoffman, E. (1975). A positron-emission

transaxial tomograph for nuclear imaging (pet). Radi-

ology.

Raichle, M. and Mintun, M. (2006). Brain work and brain

imaging. The Annual Review of Neuroscience.

Ungureanu, M., Bigan, C., Strungaru, R., and Lazarescu, V.

(2004). Independent component analysis in eeg signal

processing. MEASUREMENT SCIENCE REVIEW, 4.

Wang, L. (2005). Support Vector Machines: Theory and

Applications. Springer.

Zhukov, L., Weinstein, D., and Johnson, C. (2000). Inde-

pendent component analysis for eeg source localiza-

tion. Engineering in Medicine and Biology Magazine.

IJCCI 2009 - International Joint Conference on Computational Intelligence

482

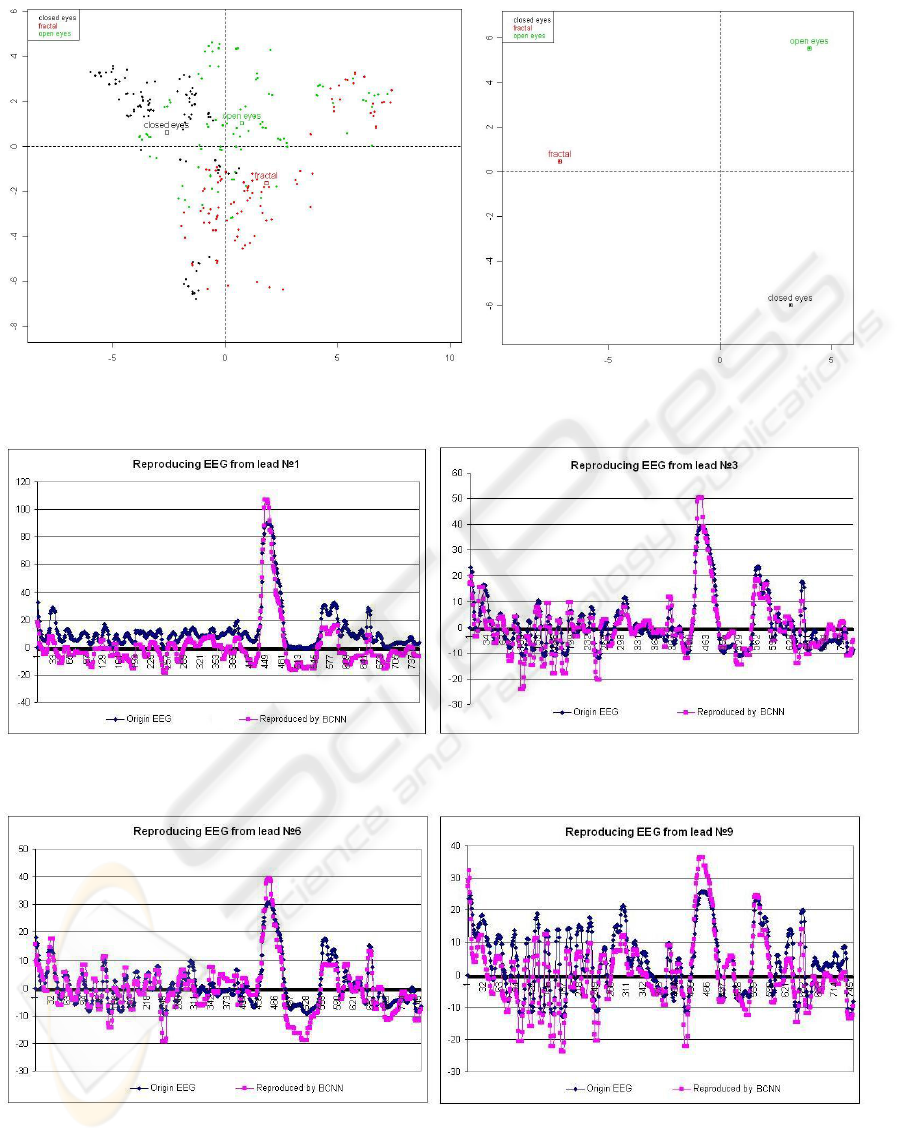
Figure 2: Principal components of brain centers interaction schema in the case of random three second cuts (left plot) and ﬁrst

three second cuts (right plot) of the EEG recording.

Figure 3: An example of an original EEG time series from 1-st and 3-d electrodes and its reproduction by BCNN-model for

“fractal” data.

Figure 4: An example of an original EEG time series from 6-th and 9-th electrodes and its reproduction by BCNN-model for

“fractal” data.

BRAIN CENTERS MODEL AND ITS APPLICATIONS TO EEG ANALYSIS

483