USING ATTAINMENT SURFACE

FOR COMPARING NSGA-II AND SPEA-II

A Case Study

Alvaro Gomes, C. Henggeler Antunes, A. Gomes Martins

Institute for Systems Engineering and Computersat Coimbra, DEEC – FCT University of Coimbra, Portugal

João Melo

DEEC – FCT University of Coimbra, Coimbra, Portugal

Keywords: Evolutionary multi-objective optimization, genetic algorithms, algorithms assessment, surface attainment.

Abstract: This paper presents a comparative analysis of the results obtained with two different genetic algorithms,

NSGA-II and SPEA-II, in the framework of load management activities in electric power systems. The

multiobjective problem deals with the identification and the selection of suitable control strategies to be

applied to groups of electric loads aimed at reducing maximum power demand at the sub-station level,

maximizing profits with selling of electricity and minimizing the discomfort caused to the end-users. The

comparative analysis of the algorithms’ performance is done based on the attainment surface approach.

Besides, it is shown that this approach can be used as a vehicle to introduce the decision maker’s

preferences in the evaluation process.

1 INTRODUCTION

In single objective optimization problems, in which

the merit of solutions is evaluated in just one axis, it

is easy to find a metric that allows different solutions

to be compared and ranked even if the optimum is

not known. However, in a multiobjective (MO)

environment a solution is evaluated according to its

performance on each of the multiple, conflicting and

incommensurate objectives under optimization.

Typically, an “optimal” point, in the sense of

optimizing simultaneously all objective functions, is

an infeasible solution in the objective function space

and it does not even exist in the decision variable

space. Therefore, the decision maker (DM) must

choose a final solution from the set of non-

dominated solutions - the Pareto front (PF) -

according to his/her preferences. However, in

MOOP, although the non-dominance concept is the

key one, it is also a “poor” one in the sense that it

does not enable discrimination between

nondominated solutions. In order to distinguish

between two non-dominated solutions the DM’s

preference structure must be taken into

consideration. The need for taking into account the

DM’s preferences also arises when comparing sets

of potential solutions.

In this context, an important issue is what

approach to use for assessing and comparing sets of

potential solutions. Several approaches have been

reported in the literature regarding the evaluation of

solutions and algorithms (Ang and Li, 2001)

(Brockhoff et al., 2008) (Fonseca and Fleming,

1996) (Hansen and Jaskiewicz, 1998) (Knowles and

Corne, 2000, 2001) (Knowles et al., 2006) (Zitzler et

al., 2000, 2003, 2008). Genetic Algorithms (GA)

while tools to compute potential solutions to a given

problem should be able to identify diverse and well-

spread solutions over the Pareto frontier and, at the

same time, solutions should be as close as possible

to the true Pareto optimal frontier (POF) (Zitzler et

al., 2000).

The identification and choice of a metric is not

easy, at least in situations where neither an optimal

point nor the true Pareto front are known - that is,

whenever no references exist that can be used for

assessing the quality of the results obtained.

In this work the attainment surface metric (AS)

is used to compare the performance of two genetic

237

Gomes A., Henggeler Antunes C., Gomes Martins A. and Melo J. (2009).

USING ATTAINMENT SURFACE FOR COMPARING NSGA-II AND SPEA-II - A Case Study.

In Proceedings of the International Joint Conference on Computational Intelligence, pages 237-242

DOI: 10.5220/0002323602370242

 SciTePress

algorithms to deal with the design and identification

of load management actions in electrical power

systems. It is shown that it is possible to use the AS

metric also as a tool to incorporate the DM’s

preferences when comparing sets of solutions. In

section 2 an overview about algorithm evaluation is

presented. In section 3 the problem under analysis is

briefly described, while the case study is introduced

in section 4. The analysis of the results is done in

section 5 and conclusions are drawn in section 6.

2 PERFORMANCE ASSESSMENT

When the true POF is not known, which is a

common situation in real-world MOOP, reference

alternatives have been used in order to overcome the

problems resulting from not knowing exactly the

Pareto front (Ang and Li, 2001)(Gomes et al., 2008).

Evaluating the results of a multiobjective problem is

itself a multiobjective problem, and intensive

research work is being carried out in order to deal

with the assessment of solutions in MOOP (Branke

et al., 2001) (Knowles and Corne, 2000,

2006)(Zitzler et al., 2000, 2008). Recently some

researchers focussed their work on comparing sets of

solutions or populations (Zitzler et al., 2003, 2008).

In the problem under study in this work, as in

many real-world problems, the POF is unknown and

the diversity and the spreading of solutions are not to

be taken for granted. Therefore, the assessment of

the algorithms performance is carried out by using

the AS concept described in Fonseca and Fleming

(1996) and extended by Knowles and Corne (2000).

If the non-dominated solutions resulting from a

multiobjective optimizer are the points P

, P

, …, P

(Figure 1) then the attainment surface is the surface

limited by the lines joining the points. This surface

divides the search space into two regions: DR is the

region of the search space dominated by solutions

computed by the algorithm, while NDR is the region

of the search space non-dominated by the solutions

computed by the algorithm. As proposed by Fonseca

and Fleming (1996), if a set of lines (Figure 1.b)

equally spread are drawn starting from the origin

towards the AS then we can compare the distance of

each AS to the origin and identify the AS that is first

intersected by each line. The number of times each

AS is first intersected by different lines enables to

compare the sets resulting from each algorithm.

Knowles and Corne (2000) extended this

analysis in the following manner. Having m runs

from each algorithm each line has 2m intersections

and a statistical univariate analysis on the

distribution of the intersections can be done

providing a measure about the performance of the

algorithms in the region of the space represented by

each line. These authors use a pair of values (a, b),

in which a represents the percentage of the space

(lines) in which the first algorithm performs better

that the second algorithm and b represents the

percentage of the space (lines) in which the second

algorithm performs better than the first one. If the

set of lines cover the whole front then the attainment

surface method allows to deal with the three issues

raised in the performance assessment: distance to the

POF, distribution and diversity of the solutions.

Figure 1: (a) Attainment surface, in a problem with two

objective functions. (b) Two different attainment surfaces

resulting from 2 different runs (two different algorithms or

the same algorithm with a different set of parameters).

The analysis done using the AS is carried out

after the simulations of the GAs, and two different

analyses are possible: one carried out in a

generational basis all over the simulation and the

other based on the last generation populations only.

Very often the POF computed is very large and

may present many solutions that are not interesting

from the DM’s perspective. An interesting situation

is the one in which it is possible to take into account

the DM’s preferences when comparing the

populations. It is possible to introduce thresholds

representing the DM’s preferences and then

computing the AS metric taking into account those

threshold levels. That is, the AS can be used as a

tool allowing both to compare the performance of

GAs and at the same time to incorporate the DM’s

preferences in the analysis, thus resulting in a

reduced set of solutions more in accordance with the

DM’s preferences. The DM is asked to provide

aspiration and/or reservation levels and the AS takes

these levels into account. The aspiration level

represents the value that the DM would like to attain

in each objective function, thus leading to the

identification of a region in the search space

containing the “better” solutions according to the

DM’s preferences. The reservation levels represent

the worst values the DM is willing to accept for each

IJCCI 2009 - International Joint Conference on Computational Intelligence

238

objective function, according to his/her knowledge

about the problem domain. Solutions that do not

attain these levels may be eventually penalized and

would be hardly chosen. A third type of threshold

may be considered denoting a “non-feasible” level,

meaning that a solution is “unfeasible” according to

the DM’s preferences (that may evolve over the

simulation/generations). These non-feasible levels

can be taken into consideration in the MO model by

imposing hard constraints at the outset, which may

later be removed or revised. In some real-world

problems the best way to deal with non-feasible

solutions if through the penalization of their fitness,

and thus give them low reproduction probability.

These solutions can exist (preferably in very low

number) in the population. These preference-driven

thresholds influence the assessment of the

algorithms done by the AS (Figure 2 and Figure 3).

In figure 2, algorithm B performs better then

algorithm A in 60% of the search space. However,

when taking into consideration the DM preference

levels the amount of space in which algorithm B

performs better then algorithm A changes

drastically. One can say that A performs better in

85% of the “space” that is more interesting from the

DM perspective, that is, 85% of the space delimited

by the reservation levels of the DM.

Figure 2: AS metric as a way to compare the algorithm

performance.

Figure 3: AS metric, taking into consideration the DM’s

preferences.

3 CASE STUDY

With the restructuring and unbundling of the

electricity sector, a common scenario is the one in

which electricity retailers buy the electricity in the

wholesale market and sell the electricity to the end-

users in the retail markets. Very often, the electricity

prices at the wholesale market change more

frequently and more intensely than at the retail

market. As most consumers buy electricity at fixed

costs (over a period of time) if retailers have the

ability to appropriately change their customer’s load

then they can take advantage of the difference of

prices between the wholesale market and the retail

market. As energy profits depend on the amount of

energy sold and the maximum peak demand, the

application of control strategies to some end-use

loads changes the demand patterns and thus changes

the profits per unit of energy sold. The aim is to

identify adequate on/off periods (load control

actions that change the regular working cycle of

end-use loads) to be implemented on a daily basis

that allow, at the same time, to reduce the maximum

power demand and to increase profits without

imposing a severe discomfort to the end-users.

These competing objectives make the design and

selection of the direct load control actions a hard

combinatorial multiobjective problem that can be

tackled by EAs.

The objective of this work is to compare the

performance of NSGA-II and SPEA-II when used in

the identification of the direct load control action to

be applied over several groups of air conditioners in

order to reduce the maximum demand of a sub-

station. The topmost issue in these activities is the

identification of suitable on/off periods to be applied

over some end-use loads (Heffner and Goldman,

2001)(Hirst and Kirby, 2001)(Gomes et al., 2004)

(Molina et al., 2004).

In this case, the pursued objectives are

minimization of maximum peak power demand in a

given substation (PD); maximizing profits with

selling of electricity (Pr); and minimizing the

eventual discomfort caused to the consumers,

measured as the maximum interval of time (MI), in

minutes, in which the room temperature was above

the comfort temperature.

Usually, the implementation of activities

involving the use of demand-side resources requires

combining several end-use loads in groups and

applying a given control strategy (set of all on/off

control periods) over each group of loads 800 air

conditioners were identified as available for control

and have been grouped as shown in table 1.

The maximum peak demand at the substation is

about 17769 kW, at 15:00h, and the maximum

demand of all air conditioners under control is about

2280 kW also occurring at 15:00h.

USING ATTAINMENT SURFACE FOR COMPARING NSGA-II AND SPEA-II - A Case Study

239

Some characteristics of the algorithm are:

• Size of the population: 30

• Stop condition: 7000 generations

• Crossover probability

o NSGA-II: 0.1; SPEA-II: 0.7

• Mutation probability: adaptive control.

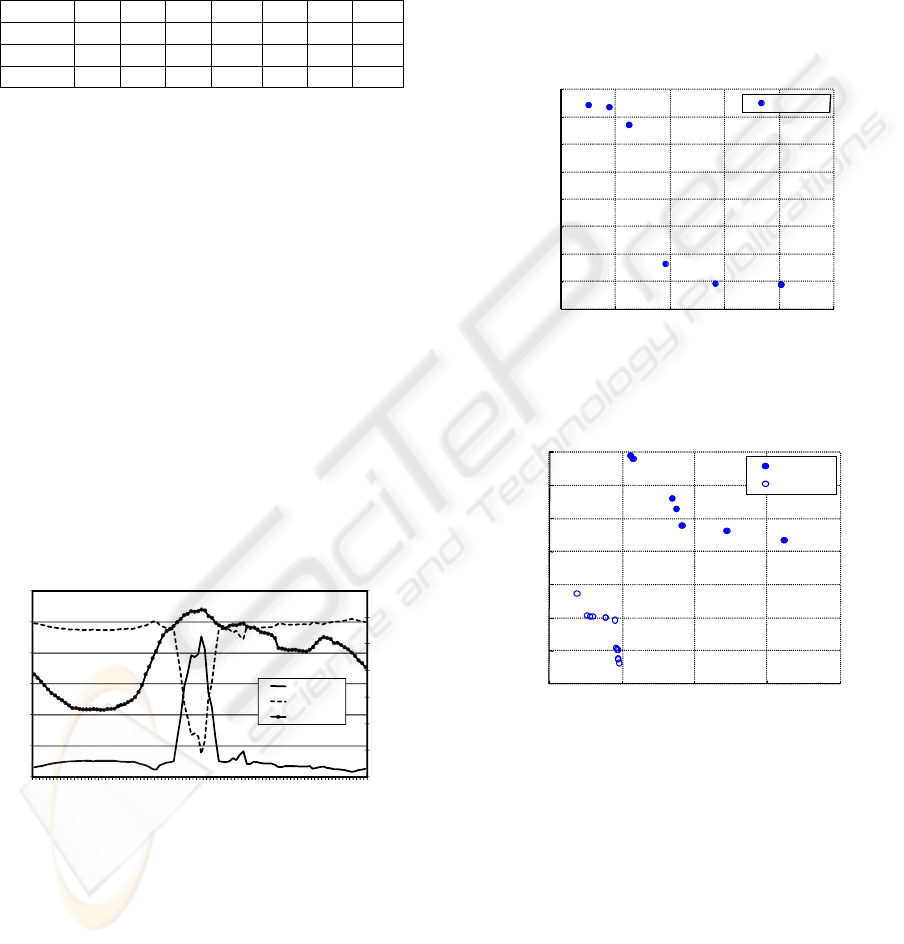
Table 1: Groups of air conditioners under control.

Groups 1 2 3 4 5 6 7

# loads 40 60 50 100 75 75 100

Groups 8 9 10 11 12 13 14

# loads 15 20 30 100 50 10 75

The values for the crossover probability in the

two algorithms are the ones that allowed obtaining

the best results in each case.

The implementation of the algorithms is slightly

different from the original implementations. The

main difference is the way the mutation operator is

constructed. In our implementation, instead of being

a fixed value the mutation operator presents an

adaptive control behaviour, in such a way that the

mutation probability of one gene may be different

from the mutation probability of other genes in the

same individual. Also, the mutation probability of

genes in one individual may be different from the

mutation probability of the genes in other

individuals in the population. Moreover, as the

binary alphabet has been used for the encoding of

individuals two different mutations can occur (0 → 1

and 1 → 0), and these two mutations may occur with

different probabilities (Figure 4).

0.0000

0.0002

0.0004

0.0006

0.0008

0.0010

0.0012

00:00

01:00

02:00

03:00

04:00

05:00

06:00

07:00

08:00

09:00

10:00

11:00

12:00

13:00

14:00

15:00

16:00

17:00

18:00

19:00

20:00

21:00

22:00

23:00

Power (MW)

Mutation probability for one individual

pm 0->1

pm 1->0

Demand SS

Figure 4: Mutation probability for one individual (showing

the values for the two mutations that can occur).

4 SOME RESULTS

The analysis is based on 7 runs for each algorithm.

The solutions computed by NSGA-II and SPEA-II

are displayed in Figures 5 - 8.

A 2D graph enables to qualitatively evaluate

each non-dominated front. As the results obtained

for objective function MI are integer values that are

multiple of 5 (5, 10, 15…), the non-dominated fronts

for different values of MI (5, 10, 15 and 20 minutes)

are shown in order to use 2D graphs. Only NSGA-II

was able to identify solutions with MI=5 minutes.

Regarding the situation MI=10 minutes, solutions

computed by SPEA-II dominate all the solutions

computed by NSGA-II. The opposite happens for

MI=15 and MI=20 minutes.

1.74 1.745 1.75 1.755 1.76 1.765

x 10

-8849

-8848.5

-8848

-8847.5

-8847

-8846.5

-8846

-8845.5

-8845

Power (kW)

Profits (Euro)

Maximum interval 5 minutes

NSGA-II

Figure 5: Results for profits and power demand

(considering maximum interval 5 minutes).

1.7 1.71 1.72 1.73 1.74

x 10

-8879

-8878

-8877

-8876

-8875

-8874

-8873

-8872

Power(kW)

Profits (Euro)

Maximum interval 10 minutes

NSGA-II

SPEA-II

Figure 6: Results for profits and power demand

(considering maximum interval 10 minutes).

With the non-dominated solutions resulting from

the 7 runs of each algorithm, the percentage of space

in which the solutions computed by NSGA-II

dominate the solutions computed by SPEA-II

(Figure 9) was calculated. NSGA-II is better in

about 35% of the space while SPEA-II performs

better in about 24%. In the remaining 41% one

cannot say that one algorithm is better than the

other.

The introduction of reservation levels (inferior

values the DM is willing to accept) leads to

IJCCI 2009 - International Joint Conference on Computational Intelligence

240

“removing” from the analysis some regions of the

search space that are not interesting to the DM when

computing the AS. In this problem the DM choose

as reservation levels the following values: 17300 kW

for peak power demand, 8860 k€ for profits and 10

for maximum interval objective. The new results for

the AS metric are shown in Figure 10.



1.67 1.675 1.68 1.685 1.69 1.695 1.7

x 10

-8918

-8916

-8914

-8912

-8910

-8908

-8906

Power(kW)

Profits (Euro)

Maximum interval 15 minutes

SPEA-II

NSGA-II

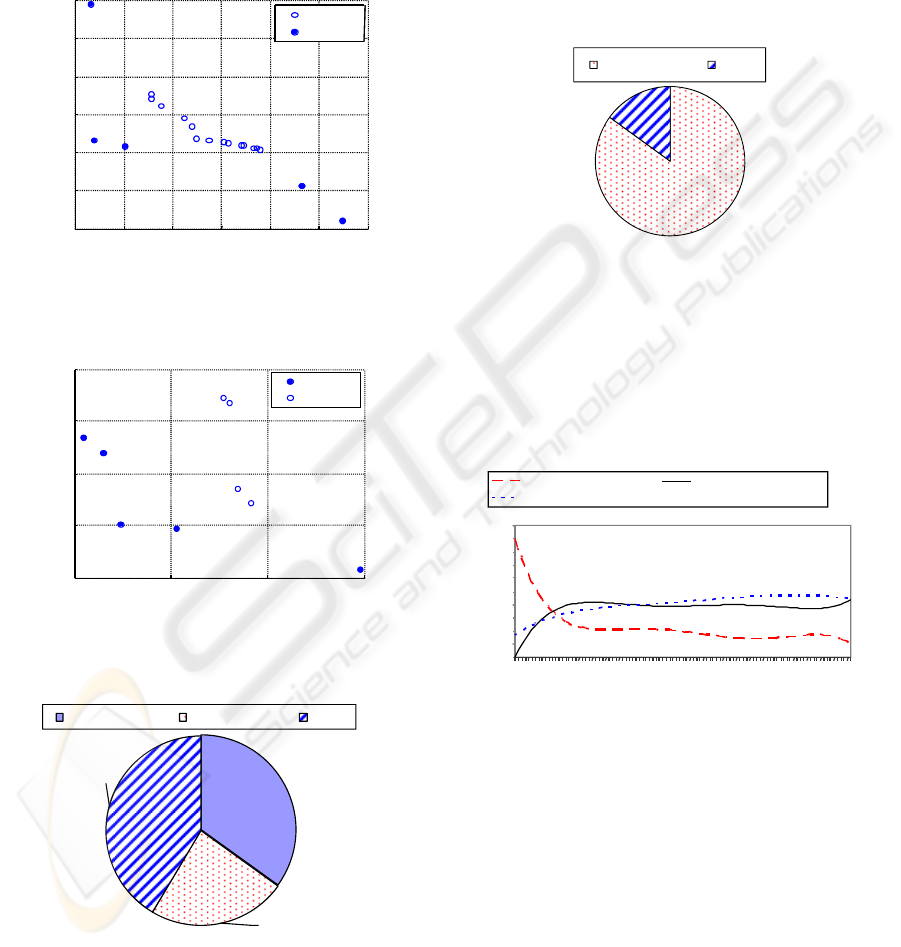
Figure 7: Results for profits and power demand

(considering maximum interval 15 minutes).



1.65 1.655 1.66 1.665

x 10

-8950

-8945

-8940

-8935

-8930

Power(kW)

Profits (Euro)

Maximum interval 20 minutes

NSGA-II

SPEA-II

Figure 8: Results for profits and power demand

(considering maximum interval 20 minutes).



35%

24%

41%

NSGA-II better SPEA-II better Equal

Figure 9: Percentage of the search space in which each

algorithm performs better.

It can be seen that solutions identified by SPEA-

II are never dominated by solutions computed by

NSGA-II and dominate the solutions computed by

NSGA-II in about 85% of the space. Introducing the

DM’s preferences in the calculation of the AS metric

causes changes in the initial results of the metric.

The two algorithms perform distinctly in different

regions of the search space, being the SPEA-II able

to compute solutions more in accordance with the

DM preferences. Probably, NSGA-II is able to

compute solutions that are very good in some

objectives but really bad in the other objectives.

85%

15%

SPEA-II better Equal

Figure 10: Percentage of the search space in which each

algorithm performs better taking into consideration the

DM preferences.

Besides applying the AS metric on the results of

the last generation of each algorithm, we have done

a generational analysis by computing the AS in each

generation by using one run of each algorithm

(Figure 11).

100

1 527 1053 1579 2105 2631 3157 3683 4209 4735 5261 5787 6313 6839

SPEA-II better then NSGA-II NSGA-II better then SPEA-II

NSGA-II equal to SPEA-II

Number of generations

Figure 11: AS computed in each generation.

We can see that after the first one thousand

generations the SPEA-II algorithm performs better

than NSGA-II only in about 15%-20% of the

objective search space while in about 40% of the

space no algorithm performs better that the other.

A generational analysis has been done based on

the minimal Euclidean distance between the

population and a reference point whose coordinates

can be the values the DM would like to attain in

each objective (aspiration levels) or, as in this case,

the best values obtained in each objective (16 500

kW; 5 minutes; 8950 k Euros) (Figure 12). The

population generated by NSGA-II always contains

USING ATTAINMENT SURFACE FOR COMPARING NSGA-II AND SPEA-II - A Case Study

241

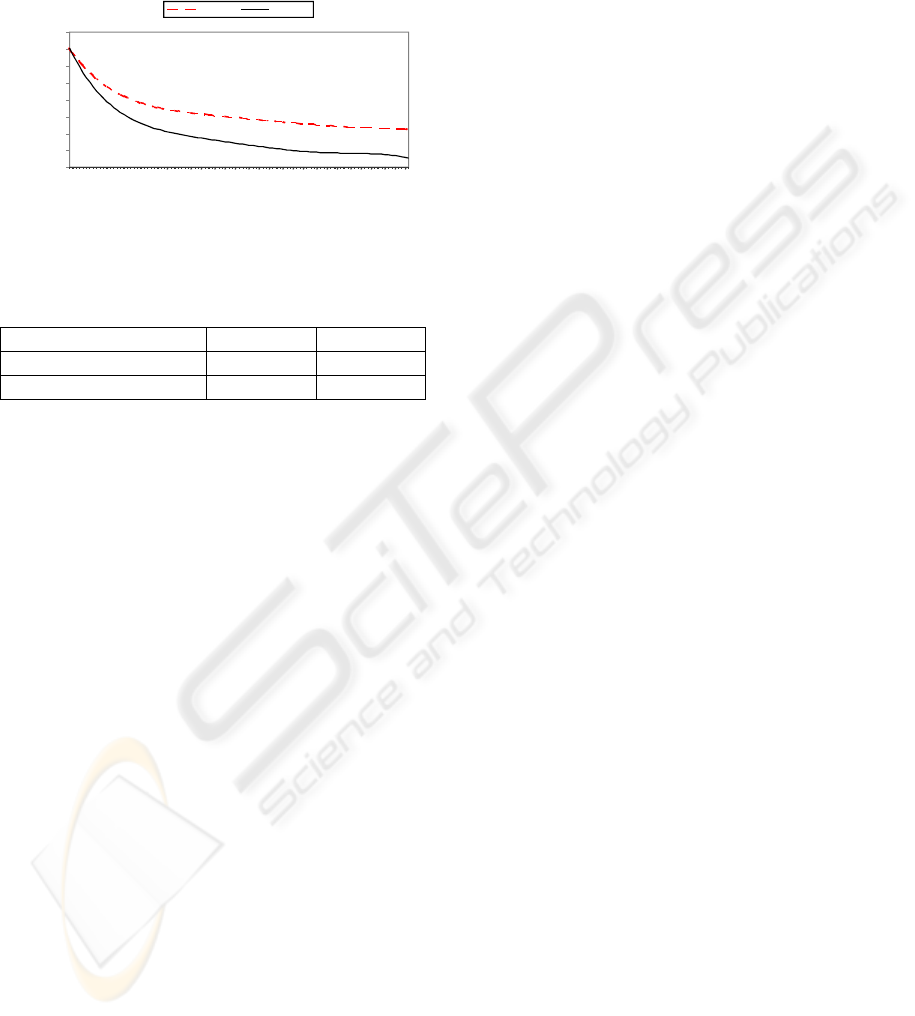
the individual(s) closer to the reference point (Fig. 12).

The impacts of the direct load control actions on

the demand are displayed in Table 1. It was possible

to reduce the maximum power demand at the sub-

station level without decreasing profits.

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1 524 1047 1570 2093 2616 3139 3662 4185 4708 5231 5754 6277 6800

SPEA-II NSGA-II

Distance to PMO

Number of generations

Figure 12: Minimal distance in each generation between

the population and the reference point.

Table 1: Impacts of direct load control actions on the

demand at the sub-station and on the profits.

Original SPEA-II

Demand at SE (kW) 17769,1 17055,8

Profits (€) 8837,74 8876,96

5 CONCLUSIONS

In this work the AS has been used to compare the

results obtained with NSGA-II and SPEA-II in the

identification of load control actions to be

implemented over groups of air conditioners. AS

allows to dealing with diversity of solutions,

distribution and proximity to the true Pareto front.

Moreover, it was possible to introduce the DM

preferences and thus reduce the number of non-

dominated solutions that the DM has to screen in

order to select one solution for implementation.

REFERENCES

Ang, K., Y. Li, 2001. “Mutil-Objective Benchmark

Studies for Evolutionary Computation”, Genetic and

Evolutionary Computation Conference, Workshop

Program, 393-396, San Francisco, California, 2001.

Branke, J., T. Kaubler and H. Schmeck, 2001. "Guidance

in Evolutionary Multi-Objective Optimization",

Advances in Engineering Software, 32.

Brockhoff, D., T. Friedrich, and F. Neumann, 2008.

“Analysing Hypervolume Indicator Based

Algorithms”, Rudolph et al. (Eds.): PPSN X, LNCS

5199, pp. 847–858, 2008.

Deb, K., S. Agrawal, A. Pratab, T. Meyarivan, 2002. “A

fast and elitist multiobjective genetic algorithm:

NSGA-II”, IEEE Transactions on Evolutionary

Computation, 6 (2), pp. 182-197.

Fonseca, C., P. Fleming (1996), “On the performance

assessment and comparison of stochastic

multiobjective optimizers”, In H.-M. Voigt, W.

Ebeling, I. Rechenberg, and H.-P. Schwefel (Eds),

Fourth International Conference on Parallel Problem

Solving from Nature (PPSN-IV), Berlin, Germany,

584-593, 1996. Springer.

Gomes, A., C. H. Antunes, A. G. Martins, 2004b. “A

multiple objective evolutionary approach for the

design and selection of load control strategies". IEEE

Transactions on Power Systems, 2004, 19(2), p. 1173-

1180.

Gomes, A., C. H. Antunes, A. G. Martins, 2008. “Design

of an Adaptive Mutation Operator in an Electrical

Load Management Case Study”. Computers and

Operations Research, 2008, 35(9), p. 2925-2936.

Hansen, M., A. Jaszkiewicz (1998), "Evaluating the

quality of approximations to the non-dominated set”,

IMM Technical Report IMM-REP-1998-7, Technical

University of Denmark, http://delta.cs.cinvestav.mx

/~coello/EMOO/EMOObib.html em 24/10/2003,

March 1998.

Heffner, G., and C. Goldman, "Demand Responsive

Programs - An Emerging Resource for Competitive

Electricity Markets?", Proceedings of the International

Energy Program Evaluation Conference (2001

IEPEC), 2001.

Hirst, E., and B. Kirby, 2001. "Retail-Load Participation

in Competitive Wholesale Electricity Markets",

Edison Electric Institute, 2001.

Knowles, J., and D. Corne, 2000. "Approximating the

Nondominated Front Using the Pareto Archived

Evolution Strategy, "Evolutionary Computation

Journal, 8, 2.

Knowles, J., and D. Corne, 2001. "On metrics for

comparing non-dominated sets”, In Congress on

Evolutionary Computation (CEC’2002), Vol 1, pp

711-716, Piscatawya, New Jersey, May 2002.

Knowles, J., L. Thiele, and E. Zitzler, 2006. “A Tutorial

on The Performance Assessment of Stochastic

Multiobjective Optimizers”, Tik Report Nº 214, 2006.

Molina, A., A. Gabaldon, C. Alvarez, J. A. Fuentes, and E.

Gómez; “A Physically Based Load Modelo f

Residential Electric Thermal Storage: Applications to

LM Programs”; International Journal of Power and

Energy Systems, Vol. 24, 1, 2004.

Zitzler, E., L. Thiele, K. Deb, 2000. "Comparison of

Multiobjective Evolutionary Algorithms: Empirical

Results", Evolutionary Computation, 8, 2, 173-195.

Zitzler, E., L. Thiele, M. Laummans, C. Fonseca and V.

Grunert da Fonseca, 2003; “Performance Assessment

of Multiobjective Optimizers: An Analysis and

Review”; IEEE Transactions on Evolutionary

Computation, vol. 7, no. 2, April 2003.

Zitzler, E., L. Thiele, and J. Bader, 2008b. “SPAM: Set

Preference Algorithm for Multiobjective

Optimization”, Rudolph et al. (Eds.): PPSN X, LNCS

5199, pp. 847–858, 2008.

IJCCI 2009 - International Joint Conference on Computational Intelligence

242