
ARTIFICIAL LIFE MODEL OF DENGUE HOST-VECTOR DISEASE
PROPAGATION
Carlos Isidoro, Nuno Fachada, F
´
abio Barata and Agostinho Rosa
LaSEEB, ISR, Instituto Superior T
´
ecnico, Av. Rovisco Pais, 1049-001 Lisboa, Portugal
Keywords:
Artificial life, Agent based modelling, Aedes aegypti, Dengue, RIDL.
Abstract:
The paper presents an agent based model of the Aedes aegypti mosquito, which considers mosquito population
dynamics and a specific population control strategy, as well the dengue propagation in mosquito (vector) and
human (host) populations. More specifically, this study concerns the impact that the RIDL strategy (Release
of Insects carrying a Dominant Lethal gene) has on the infection period among humans. The agents model the
main aspects of the mosquito’s ecology and behavior, while the environmental components are implemented
as a layer of dynamic elements obeying to physical laws. The main objective of this approach is to provide
realistic simulations of insect biologic control strategies, namely RIDL. Model verification was performed
through examination of simulation parameters variation and qualitative assessment with existing models and
simulations. The LAIS simulator was a valuable tool in this investigation, allowing efficient agent based
modeling (ABM) and simulation deployment and analysis.
1 INTRODUCTION
The dengue is a dangerous disease which still lacks a
cure, and it is spread through a specific type of vector,
the Aedes aegypti mosquito. Currently, the most af-
fected areas are the ones with tropical climates since
factors like high temperature and frequent precipita-
tion are favorable to Aedes aegypti growth. However,
if current predictions about climate change happen,
many new areas might start facing the dengue threat
(Senior, 2008).
Since an effective treatment is yet to be found,
it is particularly important to focus on prevention,
keeping the mosquito population under transmission
threshold, or better still, eradicate the disease. Vari-
ous strategies have been developed and used for this
purpose, ranging from releasing large amounts of ster-
ile mosquitoes into the environment to clearing areas
with still water that might be used as mosquito breed-
ing sites.
This paper focuses on determining the influence
the RIDL mosquito population control strategy has
on the dengue infection period in human populations.
The work presented here is a continuation of (Isidoro
et al., 2009b), which is concerned with mosquito
population dynamics, as well as the effects caused
by RIDL on such populations, and (Isidoro et al.,
2009a), which presents a study of dengue propagation
in mosquito (vector) and human (host) populations.
The state of the art in the modeling and simulation of
the Aedes aegypti mosquito, dengue transmission and
other relevant related subjects is presented in section
2; the modeling approach and the used software plat-
form are discussed in section 3, while the model itself
is described in section 4. Sections 5 and 6 present the
performed simulations, and the associated discussion,
respectively.
2 STATE OF THE ART
There have been numerous models of mosquitoes and
mosquito-borne disease, beginning with the classic
Ross-Macdonald malaria models (Ross, 1911; Mac-
donald, 1952; Macdonald, 1957) and extending to
present day models of vectors populations or aspects
of vector biology, not directly considering disease
(Eisenberg et al., 1995a; Eisenberg et al., 1995b; Alto
and Juliano, 2001; Ahumada et al., 2004).
One example of modeling the dengue vector
mosquito population dynamics is by Focks and col-
leagues (Focks et al., 1993a; Focks et al., 1993b),
examining the biology of Aedes aegypti. This is an
exceptionally detailed model, with numerous types of
containers for larval development. Hydrology (water
243
Isidoro C., Fachada N., Barata F. and Rosa A. (2009).
ARTIFICIAL LIFE MODEL OF DENGUE HOST-VECTOR DISEASE PROPAGATION.
In Proceedings of the International Joint Conference on Computational Intelligence, pages 243-247
DOI: 10.5220/0002324102430247
Copyright
c
SciTePress

levels and drying), temperature-dependent larval de-
velopment, food availability and survival are explic-
itly tracked in each container type. Detailed weather
data are used to drive the hydrological and biological
functions. This level of detail has both costs and ben-
efits; it enables consideration of detailed aspects of
the mosquito biology, but also makes true sensitivity
analysis of the model difficult or impossible. Thus,
to develop a model with this level of detail, it is nec-
essary to have extensive data available for parameter
estimates and validation.
The use of ABM methodologies to model Aedes
aegypti populations has been scarce at best. Some in-
teresting ideas are presented in a work by Deng et. al
(Deng et al., 2008), namely the use of an utility func-
tion to determine mosquito movement, taking into
account factors such as population, wind direction,
land use type and landscape roughness. However, the
practical implementation of the model is very limited,
with coarse spatial discretization (30x30) and not sin-
gular agent-based.
Models can be useful to evaluate different strategy
of mosquito control. Recently, techniques like releas-
ing genetic modified mosquitoes have been consid-
ered as an enhanced SIT to control the mosquito pop-
ulation, as the genetic manipulation in insects result
in sterility or lethal genes (Thomas et al., ; Atkinson
et al., 2007). Although there wasn’t any genetic modi-
fied mosquito open field release conducted yet, a cou-
ple of mathematical modeling works have been done
to assess the control efficacy (Esteva and Mo Yang,
2005; Li, 2004; Maiti et al., 2006). But none of those
could provide a tool to simulate the interaction be-
tween mosquito individuals such as mating behavior,
spatial distribution, and immigration etc. All these are
important for the evaluation and guidance of genetic
control approach.
3 MODELING APPROACH
The use of ABM methodologies is well suited for de-
scribing complex systems in general, being a partic-
ularly useful approach for modeling population dy-
namics and disease transmission; in such a case,
ABM provides a natural way to represent the true
diversity of intervening components, such as envi-
ronmental factors, disease vectors and disease hosts.
Other advantages include the possibility to determine
spatial behavior distribution, rapid insertion of new
components and natural consideration of non-linear
interactions between agents. This approach is not
without problems of its own: it requires considerable
computational power to simulate individual agents;
parameter tuning is not trivial; and it lacks the formal-
ism provided by differential equations, although this
issue is being addressed by recent work on ABM for-
malism (Helleboogh et al., 2007). Nonetheless, for
explicitly spatial models, such as the one presented
here, the advantages of ABM clearly outweigh its lim-
itations.
The model presented in the next section was
developed in the LAIS simulator, a multithreaded
agent based simulation platform, offering a model-
ing paradigm and a set of tools for the simulation of
complex systems (Fachada, 2008). The platform is
implemented in Java and makes use of several open
source libraries which provide tools for spatial orga-
nization and visualization, event scheduling, simula-
tion output (e.g., charts, CSV files, movies) and sim-
ple class development and instantiation using XML.
Simulations are performed in discrete time and two-
dimensional discrete space. As such, space is divided
into blocks, which are independently processed by
different threads, making LAIS scalable on modern
multiprocessor systems.
There are two main actors in the LAIS frame-
work: agents and elements. Agents are typical ABM
discrete and independent decision-making entities.
When prompted to act, each agent analyzes its cur-
rent situation (e.g. what resources are available, what
other agents are in the vicinity), and acts accord-
ingly, based on a set of rules. These rules incorporate
knowledge or theories about the respective low-level
components. On the other hand, elements are real-
valued objects which obey predetermined rules, such
as physical laws (e.g., diffusion).
4 MODEL DESCRIPTION
The Aedes aegypti LAIS model implements a square
topology where each spatial block has 8 neighbors
(N,NE,E,SE,S,SW,W,NW). Five different agents are
considered: Wild Male Mosquitoes (WM), Female
Mosquitoes (WF), Sterile Male Mosquitoes (SM),
Humans (H) and Oviposition spots (OS). Five differ-
ent elements are also used, and they fall into one of the
following categories: mosquito attractors (of which
there are three kinds), mosquito density measure and
observable mosquito properties.
The interactions between the various agents are
represented in a simplistic way in figure 1.
WM follow WF and, should they meet in the same
cell, the female has a certain chance of becoming fer-
tilized. Meanwhile the females are following Humans
and, should they meet one in the same cell they can
acquire human blood, but they also risk dying. If a
IJCCI 2009 - International Joint Conference on Computational Intelligence
244

Female
Mosquito
Sting
Human
Mating
Sterile Male
Mosquito
Wild Male
Mosquito
If fertile,
lay eggs
Eggs
Growth
Stages
Death
Figure 1: Model overview.
WF is fertilized and has acquired blood, it then moves
toward an OS to lay a certain amount of eggs, and
then goes back to the beginning of this cycle (look-
ing for humans and males). Each egg has a certain
chance of dying, and before they mature into adults
and start looking for mates, each mosquito has to go
through a number of developing stages. Each itera-
tion all mosquitoes have a certain chance to die, which
might change with the growth stage it is currently in
and the amount of mosquitoes in the area.
SM act in a similar way to WM, but a female that
mates with one does not lay eggs when it reaches an
OS.
The spread of the disease is not represented in
figure 1, but is easy to describe: whenever an in-
fected WF stings a healthy human, the human has
a chance to be infected. A non-infected WF that
stings an infectious human also has a chance to get in-
fected. WF whose progenitor was infected also have
a small chance to be born infected as well. Infected
humans are infectious for a certain number of days,
after which any WF that stings them no longer be-
comes infected. For simulations the infection can be
introduced by the addition of either infected humans
or infected WF at a user specified iteration. Location
can be random or specific.
In order for the agents to follow each other, cer-
tain elements were used. WF release Pheromone (Ph)
for the males to follow, Humans and OS release body
heat (BH) and humidity (Hu), respectively, for the fe-
males to follow. It should be noted that these elements
are used to model mosquito behavior and might not
correspond to the exact process the mosquitoes use to
follow their targets. For example, females might not
track humans based on their body heat, but through
other means, be it vision, or some other property the
female identifies. The element called body heat is
just a way to implement the ability to follow humans
that female mosquitoes show. Two more elements
are also used in the model: Density (De) and Adult
Pheromone (AP). The former is used to measure the
amount of mosquitoes in a given area, which will have
an impact on the mortality rate, and the latter is placed
by WM on themselves when they mature to inform
WF that they are suitable mates.
Element diffusion and degradation is performed
using a simple method where element concentration
in each local block is determined by eq. 1. In this
equation, C
n
is the substance concentration at tick n,
C
i
is the substance concentration at neighbor i, N is
the number of neighbor blocks (8 in this case) and α
and β are the diffusion and evaporation coefficients,
respectively.
C
t+1
= β
C
t
+ α(
N
∑
i=1
C
t
i
− C
t
)
!
(1)
WF are by far the most complex agents in the
model, but figure 2 resumes its life cycle in a clear
way. A more detailed description of each agent and
element can be found in (Isidoro et al., 2009b).
Eggs
Growth Stages
Adult: Looking
for Humans
Found a
Human?
Survives?
Successfully
stung the
Human?
Has already
mated?
Moves to
breeding site
Dies
If mate was
fertile, lay
eggs
Adult: Moving
Randomly
Found a
mate?
No
No
No
No
Yes Yes
Yes
Yes
No
Figure 2: Female Mosquito Model.
5 TESTS AND RESULTS
In order to determine the relation between the appli-
cation of a RIDL strategy and the dengue infection
period in human populations, a number of simulations
consisting of the following steps were performed: a)
start simulation with initial numbers of WM, WF and
humans; b) after the system reaches steady-state, a
number of infected WF are simultaneously released;
c) after a variable interval, the treatment (which con-
sists on the release of a fixed number of SM per day)
starts. The fixed simulation parameters are given in
table 1, while the interval between the release of in-
fected WF and beginning of treatment (no treatment
interval) varies from 0 to 20 days, with a step of 5
days. For each value of the no treatment interval,
40 simulations were performed. In this model, each
block represents around 100 square meters, and each
ARTIFICIAL LIFE MODEL OF DENGUE HOST-VECTOR DISEASE PROPAGATION
245
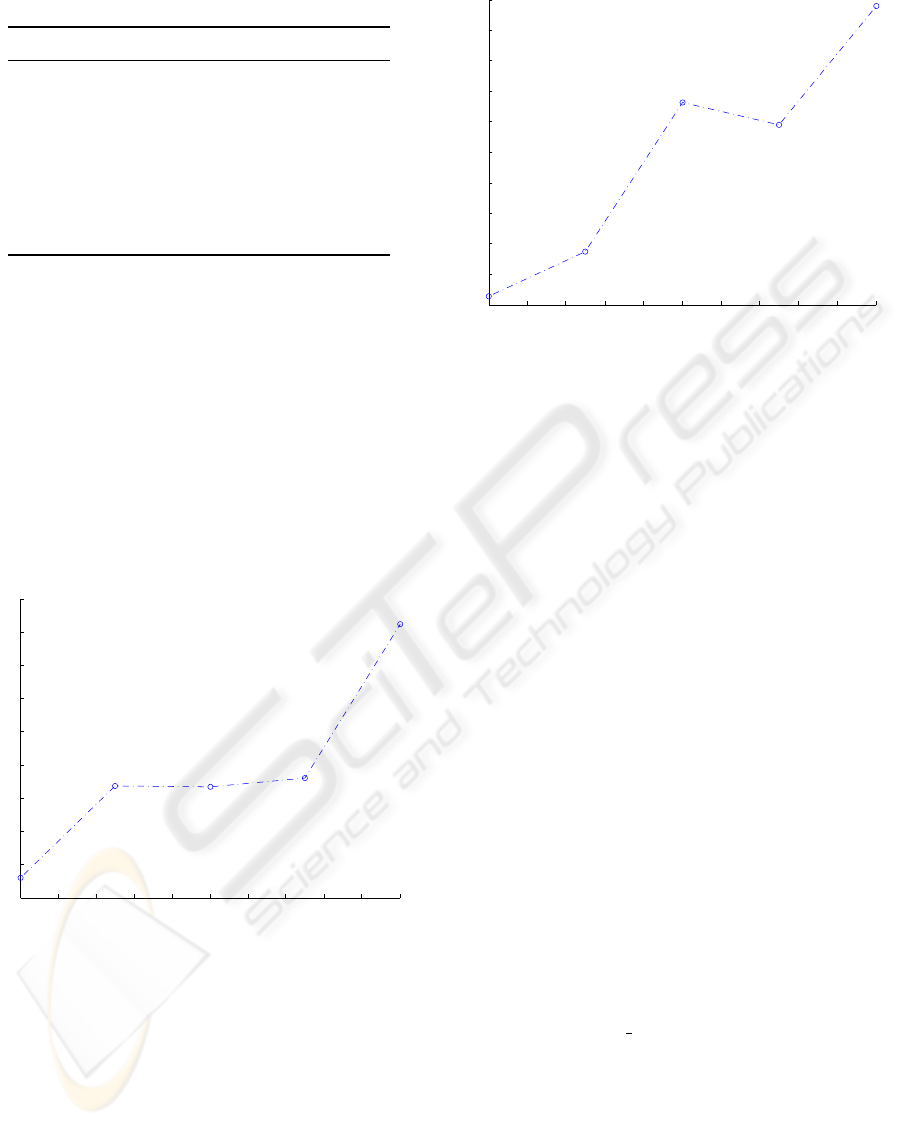
Table 1: Model parameters.
Parameter Value
Model width (blocks) 100
Model height (blocks) 100
Initial number of WM 1250
Initial number of WF 750
Initial number of Humans 700
Number of infected WF released
a
10
Number of SM released per day
b
300
Contagious period in humans (days) 12
c
a
Number of infected WF simultaneously released
after the system as reached steady-state.
b
Number of SM simultaneously released per day
after the treatment starts.
c
(Isidoro et al., 2009a)
iteration corresponds to a single day (Isidoro et al.,
2009b).
Fig. 3 shows the relation between the average in-
fection period in the human population and the no
treatment interval and fig. 4 shows the average num-
ber of infected humans as function also of the interval
without treatment.
0 2 4 6 8 10 12 14 16 18 20
27
28
29
30
31
32
33
34
35
36
No Treatment Interval
Infection Period
Figure 3: Relation between the infection period and
the no treatment interval.
6 DISCUSSION
Both figure 3 and 4 show an increasing trend of out-
come of the infection period with the delay of the
treatment in average duration and average number of
humans infected. The simulations results suggest the
earliest deployment of this specific treatment and each
day of delay the infection period is also increased for
half a day.
0 2 4 6 8 10 12 14 16 18 20
5.9
6
6.1
6.2
6.3
6.4
6.5
6.6
6.7
6.8
6.9
No Treatment Interval
Total of Infected Humans
Figure 4: Relation between the number of humans in-
fected and the no treatment interval.
Current results without validation with field sam-
pled real data can only be used for a qualitative eval-
uation of the model.
7 CONCLUSIONS AND FUTURE
WORK
The model presented in this paper can be improved
by taking into account other factors, of which envi-
ronmental aspects like temperature, precipitation and
wind are probably the most important.
In the virus, host and vector relationships, many
aspects could be added in expense of simulation time.
It would be interesting to include immune status of
the human population, the density distribution and
movement of human hosts, the virulence of the virus
strains, the characteristics of mosquito-human inter-
action and also mosquito-virus interaction.
ACKNOWLEDGEMENTS
This work was partially supported by Fundac¸
˜
ao para
a Ci
ˆ
encia e a Tecnologia (ISR/IST plurianual fund-
ing) through the POS Conhecimento Program that in-
cludes FEDER funds. The authors C. Isidoro and F.
Barata acknowledge their grant BII-2009 to Fundac¸
˜
ao
para a Ci
ˆ
encia e Tecnologia (FCT). The author N.
Fachada acknowledges its grant SFRH / BD / 48310 /
2008 to Fundac¸
˜
ao para a Ci
ˆ
encia e Tecnologia (FCT).
IJCCI 2009 - International Joint Conference on Computational Intelligence
246

REFERENCES
Ahumada, J., Lapointe, D., and Samuel, M. (2004). Mod-
eling the population dynamics of Culex quinquefas-
ciatus (Diptera: Culicidae), along an elevational gra-
dient in Hawaii. Journal of medical entomology,
41(6):1157–1170.
Alto, B. and Juliano, S. (2001). Precipitation and tem-
perature effects on populations of Aedes albopictus
(Diptera: Culicidae): implications for range expan-
sion. Journal of medical entomology, 38(5):646–656.
Atkinson, M., Su, Z., Alphey, N., Alphey, L., Coleman,
P., and Wein, L. (2007). Analyzing the control of
mosquito-borne diseases by a dominant lethal genetic
system. Proceedings of the National Academy of Sci-
ences, 104(22):9540–9546.
Deng, C., Tao, H., and Ye, Z. (2008). Agent-based modeling
to simulate the dengue spread. 7143:714310.
Eisenberg, J., Reisen, W., and Spear, R. (1995a). Dy-
namic model comparing the bionomics of two iso-
lated Culex tarsalis (Diptera: Culicidae) populations:
model development. Journal of Medical Entomology,
32(2):83–97.
Eisenberg, J., Reisen, W., and Spear, R. (1995b). Dynamic
model comparing the bionomics of two isolated Culex
tarsalis (Diptera: Culicidae) populations: sensitivity
analysis. Journal of medical entomology, 32(2):98–
106.
Esteva, L. and Mo Yang, H. (2005). Mathematical model to
assess the control of Aedes aegypti mosquitoes by the
sterile insect technique. Mathematical biosciences,
198(2):132–147.
Fachada, N. (2008). Agent-based Simulation of the Immune
System. Master’s thesis, Instituto Superior T
´
ecnico,
Lisboa.
Focks, D., Haile, D., Daniels, E., and Mount, G. (1993a).
Dynamic life table model of a container-inhabiting
mosquito, Aedes aegypti (L.)(Diptera: Culicidae).
Part 1. Analysis of the literature and model devel-
opment. Journal of Medical Entomology, 30:1003–
1017.
Focks, D., Haile, D., Daniels, E., and Mount, G. (1993b).
Dynamic life table model of a container-inhabiting
mosquito, Aedes aegypti (L.)(Diptera: Culicidae).
Part 2. Simulation results and validation. Journal of
Medical Entomology, 30:1018–1028.
Helleboogh, A., Vizzari, G., Uhrmacher, A., and Michel,
F. (2007). Modeling dynamic environments in multi-
agent simulation. Autonomous Agents and Multi-
Agent Systems, 14(1):87–116.
Isidoro, C., Fachada, N., Barata, F., and Rosa, A. (2009a).
Agent-based model of Dengue disease transmission
by Aedes aegypti populations (ACCEPTED). In Lec-
ture Notes in Computer Science. Springer.
Isidoro, C., Fachada, N., Barata, F., and Rosa, A. (2009b).
Agent-based model of Aedes aegypti Population Dy-
namics (ACCEPTED). In Lecture Notes in Artificial
Intelligence. Springer.
Li, J. (2004). Simple mathematical models for interacting
wild and transgenic mosquito populations. Mathemat-
ical biosciences, 189(1):39–59.
Macdonald, G. (1952). The analysis of equilibrium in
malaria. Trop Dis Bull, 49(9):813–829.
Macdonald, G. (1957). The epidemiology and control of
malaria.
Maiti, A., Patra, B., and Samanta, G. (2006). Sterile insect
release method as a control measure of insect pests: A
mathematical model. Journal of Applied Mathematics
and Computing, 22(3):71–86.
Ross, R. (1911). The Prevention of Malaria.
Senior, K. (2008). Climate change and infectious disease:
a dangerous liaison. The Lancet Infectious Diseases,
8(2):92 – 93.
Thomas, D., Donnelly, C., Wood, R., and Alphey, L. In-
sect population control using a dominant, repressible,
lethal genetic system. Science, 287(5462):2474–2476.
ARTIFICIAL LIFE MODEL OF DENGUE HOST-VECTOR DISEASE PROPAGATION
247
