
EVOLVING EFFECTIVE BIDDING FUNCTIONS FOR AUCTION
BASED RESOURCE ALLOCATION FRAMEWORK
Mohamed Bader-El-Den and Shaheen Fatima
Department of Computer Science, Loughborough University, Leicestershire LE11 3TU, U.K.
Keywords:
Genetic programming, Multi-agent systems, Resource allocation, Timetabling, Auctions based systems,
Heuristics.
Abstract:
In this paper, we present an auction based resource allocation framework. This framework, called GPAuc,
uses genetic programming for evolving bidding functions. We describe GPAuc in the context of the exam
timetabling problem (ETTP). In the ETTP, there is a set of exams, which must be assigned to a predefined
set of slots. Here, the exam time tabling system is the seller that auctions a set of slots. The exams are
viewed as the bidding agents in need of slots. The problem is then to find a schedule (i.e., a slot for each
exam) such that the total cost of conducting the exams as per the schedule is minimised. In order to arrive
at such a schedule, we need to find the bidders’ optimal bids. This is done using genetic programming. The
effectiveness of GPAuc is demonstrated experimentally by comparing it with some existing benchmarks for
exam time-tabling.
1 INTRODUCTION
Decentralised scheduling is the problem of allocat-
ing resources to alternative possible uses over time,
where competing uses are represented by autonomous
agents. This scheduling can be done using differ-
ent methods such as such as first-come first-served,
priority-first, and combinations thereof. But, these
methods do not generally possess globally efficient
solutions. Due to this limitation, considerable re-
search is now focussing on the use of market mech-
anisms for distributed resource allocation problems
(Krishna, 2002). Market mechanisms use prices de-
rived through distributing bidding protocols, such as
auctions, to determine schedules.
In an auction, there are two types of agents: the
auctioneer and the bidders. The auctioneer could be
a seller of a resource and the bidders are buyers that
are in need of the resource. The bidders bid for the re-
source being auctioned and one of them is selected as
the winner. An agent’s bid, in general, indicates the
price it is willing to pay to buy the resource. On the
basis of the agent’s bids, the resource is allocated to
the winning agent. The auction protocol determines
the rules for bidding and also for selecting a winner.
There are several protocols such as the English auc-
tion, the Dutch auction, and the Vickrey auction pro-
tocol (Krishna, 2002).
Given an auction protocol, a key problem for the
bidders is to find an optimal bidding function for the
protocol (Krishna, 2002). An agent’s bidding func-
tion is a mapping from its valuation or or utility or
preference (for the resource being auctioned) to a bid.
An agent’s valuation is a real number and so is its bid.
Since there are several agents bidding for a single re-
source, an agent must decide how much to bid so that
its chance of winning is maximized and the price at
which it wins is minimised. Such a bid is called the
agent’s optimal bid. An agent’s optimal bidding func-
tion is then the function that takes the valuation as
input and returns its optimal bid.
For a single auction, finding an agent’s optimal
bidding function is easy. But in the context of the
distributed scheduling problem we focus on, there are
several auctions that are held sequentially one after
another. Furthermore, an agent may need more than
one resource and must therefore bid in several auc-
tions. In such cases, an agent’s bidding function de-
pends on several parameters such as how many auc-
tions will be held, how many bidders will bid in each
of these auctions, and how much the agent and the
other bidders value the different resources. This com-
plicates the problem of finding optimal bids. In order
to overcome this problem, our objective is to use GP
to evolve bidding functions.
We study the distributed scheduling problem in
310
Bader-El-Den M. and Fatima S. (2009).
EVOLVING EFFECTIVE BIDDING FUNCTIONS FOR AUCTION BASED RESOURCE ALLOCATION FRAMEWORK.
In Proceedings of the International Joint Conference on Computational Intelligence, pages 310-313
DOI: 10.5220/0002324203100313
Copyright
c
SciTePress

the context of the famous exam time tabling prob-
lem (ETTP) (Carter et al., 1996). The ETTP can be
viewed as a decentralised scheduling problem where
the exams represent independent entities (users) in
need of resources (slots) with possibly conflicting and
competing schedule requirements. The problem is
then to assign exams to slots (i.e., find a schedule)
such that the total cost of conducting the exams as per
the schedule is minimised.
2 EXAM TIMETABLING
PROBLEM
The exam timetabling problem is a common problem
in most educational institutions. Although the prob-
lem’s details tend to vary from one institution to an-
other, the core of the problem is the same. There is a
set of exams (tasks), which have to be assigned to a
predefined set of slots and rooms (resources).
In our research we will be using on the follow-
ing formulation for the exam timetabling problem.
The problem consists of the a set of n exams E =
{e
1
, . . . e
n
}, a set of m students S = {s
1
, . . . s
m
}, a set
of q time slots P = {p
1
, p
2
, . . . p
q
} and a registration
function R : S → E, indicating which student is attend-
ing which exam. Seen as a set R = {(s
i
, e
j
) : 1 ≤ i ≥
m, 1 ≤ j ≥ n}, where student s
i
is attending exam e
j
.
A scheduling algorithm assigns each exam to a cer-
tain slot. A solution then has the form O : E → P or,
as a set, O = {(e
k
, p
l
) : 1 ≤ k ≥ n, 1 ≤ l ≥ q}.
The problem is similar to the graph colouring
problem but it includes extra constraints, as shown by
Welsh and Powell (Welsh and Powell, 1967). These
constraints are categorised into two main types: (a)
Hard Constraints, violating any of these constraints
is not permitted since it would lead to an unfeasible
solution, and (b) Soft Constraints, which are desir-
able but not crucial requirements. Violating any of the
soft constraints will only affect the solution’s quality.
All hard constraints are equally important, while soft
constraints are not. The importance of soft constraints
vary. Usually a cost function is designed to calculate
the cost of violating each of the soft constraints. So-
lutions with lower cost have better quality.
In general, there are two phases in solving
scheduling problems, construction phase for generat-
ing initial solution, the second phase is to improve the
quality of the initially constructed solutions, method
we present here is for the first phase.
3 AUCTION BASED
TIMETABLING
We call our exam time tabling system GPAuc. In
GPAuc, the seller is the exam time tabling system
(ETTS) and it auctions the slots one at a time. The
exams are the bidders. Every slot could be sold more
than once (because one slot could contain more than
one conflicting exam), but in each auction the slot
could be sold only for one exam. For an auction, the
winning bid is determined as follows. If the highest
bid does not increase the solution cost beyond a cer-
tain limit (Accepted-Cost), the highest bid becomes
the winning bid. Otherwise, the same rule is applied
to the second highest bid. If the second highest bid
causes the cost to increase beyond the Accepted-Cost,
the slot is left unsold and the next auction is initiated
for the followingslot. If no slots havebeen sold in full
round on all available slot, in this case the Accepted-
Cost are increased. this process is repeated till all ex-
ams are scheduled, or reaching a deadlock, where no
more exams could be scheduled without violating a
hard constraint.
The cost for a schedule is calculated using the fol-
lowing function (Carter et al., 1996):
Cost =
1
S
N−1
∑
i=1
N
∑
j=i+1
[w(|p
i
− p
j
|)a
ij
] (1)
where N is the total number of exams in the problem,
S the total number of students, a
ij
is the number of
students attending both exams i and j, p
i
is the time
slot where exam i is scheduled, w(|p
i
− p
j
|) returns
2
5−|p
i
−p
j
|
if |p
i
− p
j
| ≤ 5, and 0 otherwise.
3.1 Optimisation via Genetic
Programming
GP (Koza, 1992; Langdon and Poli, 2002; Poli et al.,
2008) is an evolutionary algorithm which is inspired
by biological evolution. The target of a GP system
is to find computer programs that perform a user-
defined task. It is a specialisation of genetic algo-
rithms where each individual is a computer program.
GP is a machine learning technique used to optimise
a population of computer programs depending on a
fitness function that measures the program’s perfor-
mance on a given task. Tree presentation of the indi-
viduals is the most common presentation which also
we will be using here. The function and terminal set
used is shown in table 1, the terminal set are inspired
from some standard graph coloring heuristics.
The GP’s fitness function we used is the follow-
ing:
EVOLVING EFFECTIVE BIDDING FUNCTIONS FOR AUCTION BASED RESOURCE ALLOCATION
FRAMEWORK
311
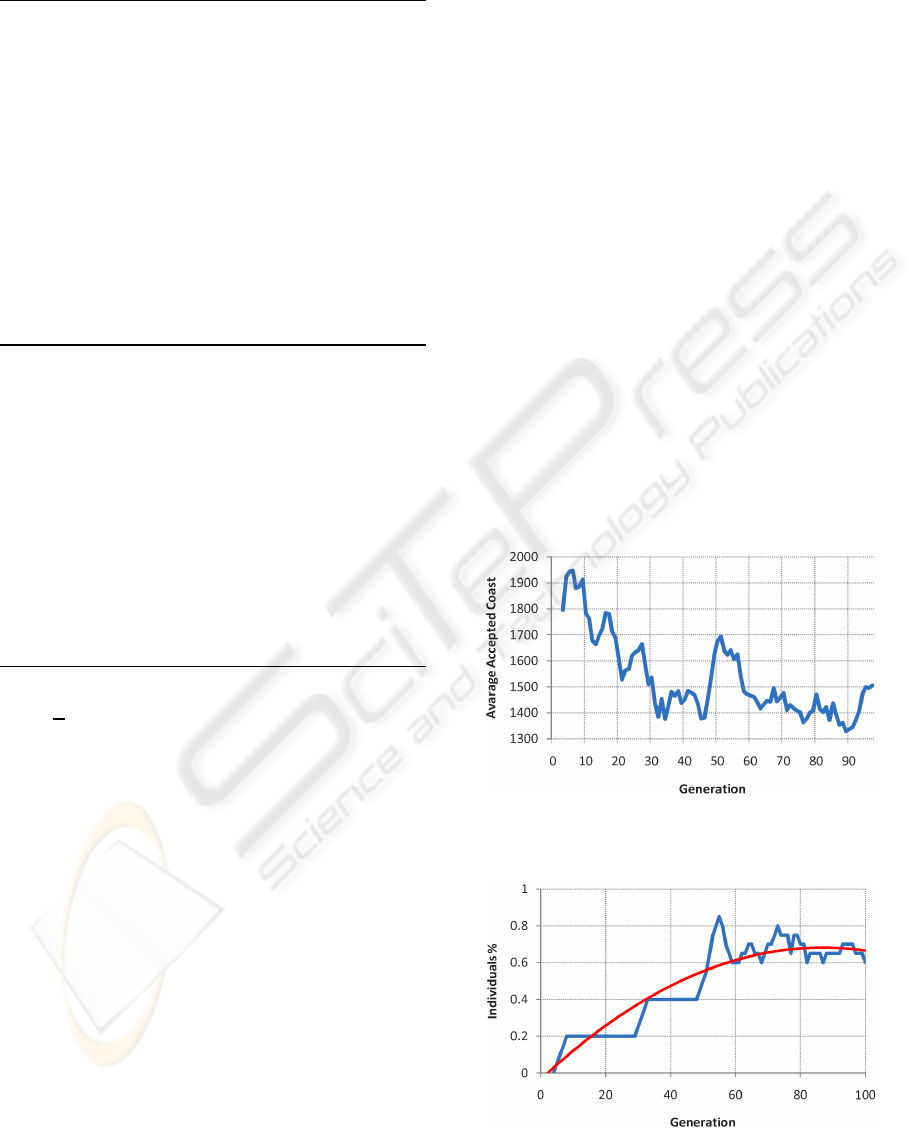
Table 1: GP function and terminal sets.
Function Set
add(d
1
, d
2
) : returns the sum of d
1
and d
2
sub(d
1
, d
2
) : subtracts d
2
from d
1
mul(d
1
, d
2
) : returns the multiplication of d
1
by d
2
div(d
1
, d
2
) : protected division of d
1
by d
2
abs(d
1
) : returns the absolute value of d
1
neg(d
1
) : multiplies d
1
by −1
fneg(d
1
) : abs(d
1
) multiplied by −1, to
force
negative value
sqrt(d
1
) : returns the a protected square
root of d
1
Terminal Set
slt : total number of available slots
for the currently bidding exam e
std : the total number of students at-
tending the bidding exam e
conf : the total number of all exams
(scheduled and not scheduled)
in conflict with exam e
cSched : number of already scheduled
exams that are in conflict with e
cPendd : number of exams(not scheduled
yet) that are in conflict with e
cost : current increase in the cost if e
is allocated the current slot
f = [
1
S
M−1
∑
i=1
M
∑
j=i+1
w(|p
i
− p
j
|)a
ij
] + (N − M) ×C (2)
where: N is the total number of exams in the prob-
lem, M is the total number of exams that have been
successfully scheduled, (N − M) ≥ 0 is the number of
unscheduled exams, C is constant. The objective is to
minimise this equation, so the lower the fitness value
the better the individual is.
The first part of the fitness function in Equation (2)
is almost the same as the cost function in Equation 1.
The second part adds extra penalty for each unsched-
uled exam. Even though solutions with unscheduled
exams are considered to be invalid solutions, this ex-
tra penalty for unscheduled exams is introduced to
give GP better ability to differentiate between indi-
viduals.
3.2 Experimental Results
We tested our method for timetabling by applying it
to one of the most widely used benchmarks in exam
timetabling, against which many state-of-the-art algo-
rithms have been compared in the past. the bench-
mark’s details could be found in (Carter et al., 1996)
where it was first introduced.
We ran a number of experiments using differ-
ent GP parameters, with population size varies be-
tween 50 to 1000, number of generations range be-
tween 50 and 100, the production and mutation rate is
5% or 10% of the total population, and 80% for the
crossover rate. The selection is done using tourna-
ment selection of 5.
Table 2 shows the cost (using equation number
(2)) of the GPAuc compared to a number of other
construction techniques, as it could be noticed the
GPAuc is very competitive with other methods tak-
ing in consideration that GPAuc does not use back-
tracking. Moreover, GPAuc is as distributed methods
and that all biding functions are automatically evolved
without human interaction.
Figures 1, 2, 3 and 4 provide some analysis
into the behaviour of the best performing individ-
uals throughout the generations. These graphs are
drawn from evolving biding functions on the York83
instance, with population size 500, number of gener-
ations 100, mutation and reproduction rate 10% and
crossover rate of 90%.
Figure 1: The average value of the final Accepted cost of
the best evolved functions.
Figure 2: Percentage of individuals that have been able to
schedule all exams in the best evolved function
IJCCI 2009 - International Joint Conference on Computational Intelligence
312

Table 2: Results from the GP-HH for time tabling among with other results reported in literature on benchmark exam
timetabling problems, the table shows the cost for each case, the cost is calculated using equation 1
car91 car92 ear83 hec92 kfu93 lse91 sta83 tre92 uta93
GPAuc 7.03 5.80 41.2 13,01 15.90 13.01 157.3 9.32 3.82
(Burke et al., 2007) 5.41 4.84 38.19 12.72 15.76 13.15 141.08 8.85 3.88
(Asmuni et al., 2004) 5.20 4.52 37.02 11.78 15.81 12.09 160.42 8.67 3.57
(Carter et al., 1996) 7.10 6.20 36.40 10.80 14.00 10.50 161.50 9.60 3.50
(Burke et al., 2007) 5.41 4.84 38.84 13.11 15.99 13.43 142.19 9.2 4.04
Figure 3: Average number of remaining exams in all best
behaving individuals.
Figure 4: Average number of all auction taking place in best
performing heuristics through out all the generations.
4 CONCLUSIONS
In this paper we introduced GPAuc, a genetic pro-
gramming framework for evolving agent’s bidding
function for resource allocation problems. The frame-
work is described in the context of the exam time
tabling problem.
Results shows that the framework is competitive
with other existing methods for constructing exam
timetables, taking in consideration that the GPAuc has
no backtracking and uses a distributed approach.
REFERENCES
Asmuni, H., Burke, E. K., Garibaldi, J. M., and McCol-
lum, B. (2004). Fuzzy multiple heuristic orderings for
examination timetabling. In Burke, E. K. and Trick,
M. A., editors, PATAT, volume 3616 of Lecture Notes
in Computer Science, pages 334–353. Springer.
Burke, E. K., McCollum, B., Meisels, A., Petrovic, S., and
Qu, R. (2007). A graph-based hyper-heuristic for ed-
ucational timetabling problems. European Journal of
Operational Research, 176(1):177–192.
Carter, M. W., Laporte, G., and Lee, S. Y. (1996). Ex-
amination timetabling: Algorithmic strategies and ap-
plications. Journal of Operational Research Society,
47:73–83.
Koza, J. R. (1992). Genetic Programming: On the Pro-
gramming of Computers by Means of Natural Selec-
tion. MIT Press, Cambridge, MA, USA.
Krishna, V. (2002). Auction Theory. Academic Press.
Langdon, W. B. and Poli, R. (2002). Foundations of Genetic
Programming. Springer-Verlag.
Poli, R., Langdon, W. B., and McPhee, N. F. (2008). A
field guide to genetic programming. Published via
http://lulu.com and freely available at http://www.gp-
field-guide.org.uk.
Welsh, D. and Powell, M. (1967). An upper bound for
the chromatic number of a graph and its applica-
tion to timetabling problems. The Computer Journal,
10(1):85–87.
EVOLVING EFFECTIVE BIDDING FUNCTIONS FOR AUCTION BASED RESOURCE ALLOCATION
FRAMEWORK
313
