
FORECASTING WITH NEUROSOLVER
Andrzej Bieszczad
Computer Science, California State University Channel Islands, One University Drive, Camarillo, CA 93012, Canada
Keywords: Forecasting, Neural network, Neuromorphic systems, General problem solvers, Predicting future,
Behavioral patterns.
Abstract: Neurosolver is a neuromorphic planner and a problem solving system. It was tested on several problem
solving and planning tasks such as re-arranging blocks and controlling a software-simulated artificial rat
running in a maze. In these tasks, the Neurosolver created models of the problem as temporal patterns in the
problem space. These behavioral traces were then used to perform search and generate actions. While
exploring general problem capabilities of the Neurosolver, it was observed that the traces of the past in the
problem space can also be used for predicting future behavioral patterns. In this paper, we present an
analysis of these capabilities in context of the sample data sets made available for the NN5 competition.
1 INTRODUCTION
The goal of the research that led to the original
introduction of Neurosolver, as reported in
(Bieszczad and Pagurek, 1998), was to design a
neuromorphic device that would be able to solve
problems in the framework of the state space
paradigm (Newell and Simon, 1963). In that
paradigm, the states of a system are expressed as
points in an n-dimensional space. Trajectories in
such spaces formed by state transitions represent
behavioral patterns of the system. A problem is
presented in this paradigm as a pair of two state: the
current state and the desired, or goal, state. A
solution to the problem is a trajectory between the
two states in the state space. Fundamentally, we are
asking how to achieve the goal state of the system
given its starting state.
The Neurosolver can solve such problems by
traversing the recorded trajectories as described in
section 2. In this paper, we demonstrate how the
very trajectories can be used for forecasting.
The original research on Neurosolver modelling
was inspired by Burnod’s monograph on the
workings of the human brain (Burnod, 1988). The
class of systems that employ state spaces to present
and solve problems has its roots in the early stages
of AI research that derived many ideas from the
studies of human information processing; e.g., on
General Problem Solver (GPS) (Newell and Simon,
1963). This pioneering work led to very interesting
problem solving (e.g. SOAR (Laird, Newell, and
Rosenbloom, 1987)) and planning systems (e.g.
STRIPS (Nillson, 1980).
The Neurosolver employs activity spreading
techniques that have their root in early work on
semantic networks (e.g., (Collins and Loftus, 1975)
and (Anderson, 1983)).
2 NEUROSOLVER
2.1 Neurosolver as a GPS
The Neurosolver is a network of interconnected
nodes. Each node is associated with a state in a
problem space. In its original application, the
Neurosolver is presented with a problem by two
signals: the goal associated with the desired state
and the sensory signal associated with the current
state. A sequence of firing nodes that the
Neurosolver generates represents a trajectory in the
state space. Therefore, a solution to the given
problem is a succession of firing nodes starting with
the current node and ending with the goal node.
The node used in the Neurosolver is based on a
biological cortical column (references to the relevant
neurobiological literature can be found in (Bieszczad
and Pagurek, 1998)). It consists of two divisions: the
upper and the lower, as illustrated in Figure 1. The
upper division is a unit integrating internal signals
from other upper divisions and from the control
386
Bieszczad A. (2009).
FORECASTING WITH NEUROSOLVER.
In Proceedings of the International Joint Conference on Computational Intelligence, pages 386-393
DOI: 10.5220/0002325303860393
Copyright
c
SciTePress

Figure 1: An artificial cortical column.
center providing the limbic input (i.e., a goal or -
using more psychological terms - a drive or desire).
The activity of the upper division is transmitted to
the lower division where it is subsequently
integrated with signals from other lower divisions
and the thalamic input. The upper divisions
constitute a network of units that propagate search
activity from the goal, while the lower divisions
constitute a network of threshold units that integrate
search and sensory signals, and generate sequences
of firing nodes. The output of the lower division is
the output of the whole node. An inhibition
mechanism prevents cycles and similar chaotic
behavior. Simply, a node stays desensitized for a
certain time after firing.
2.2 Neurosolver as a Forecaster
Normally, in the goal-oriented problem solving the
flow of activity from the upper to the lower division
is limited. This mode of operation can be described
as exploration of possibilities and looking for
environmental cues. The cues come as thalamic
input from the sensory apparatus. Often though, we
operate without far reaching goals forcing our brains
to make predictions based on the knowledge of the
past and the currently observed facts. In the
Neurosolver, similar phenomenon may be observed
if the activity in the upper division is gradually
increased, and at the same time is allowed to be
transmitted in its entirety from the upper to the lower
division. Assuming that that activity is allowed to
grow above the firing threshold level hosted by the
lower division, a node may fire without extra signals
from the sensors, or even in absence of the thalamic
input whatsoever. In this paper, we explore this
capability to predict future outcomes based on the
statistical model built in the Neurosolver.
3 DATA SETS
I presented the ideas on using the Neurosolver in
the forecasting capacity at ISF‘2008 (Bieszczad,
2008). I was encouraged to test the ideas on the data
set that was used for the NNx competition. The last
published data set is for NN5 that was held in 2008.
For this work, I assembled a research group that is
acknowledged in the later section this paper.
The NN5 data set is actually a collection of
records of daily witdrawals from a number of ATM
machines in England over a two-year period. A set
from an individual machine is divided into a larger
training part collected over two years and smaller
test part collected over two months. Each set is a
time series that represents a temporal usage pattern
of that particular machine. That temporal nature of
the patterns was what caught our attention in the
context of the Neurosolver.
We started with the use the data in their raw
format by assigning each datum to a Neurosolver
node. In that sense, each datum is a state of the
system in the progression of states as specified by
the given time series. The Neurosolver therefore
learns the trajectory that corresponds to each training
time series, and over time generalizes the trajectories
to represent all time series by it adaptation rules.
Due to the large number of data points and the
proximity of some of them, we also tried to cluster
the data with several cluster sizes. For that, we
approximated the k-neighbor algorithm by one that
is very straighforward in one dimension. Simply, we
decided on an arbitrary number of clusters, and then
recursively dividing the data set in two allocating the
number of clusters for each of the two division
according to the data density. An example of this
process is shown in Figure 2.
A simpler approach to clustering is to divide the
domain into a number of equal segments and then
create clusters based on the data membership in the
clusters. However, the problem with this approach is
that is does not take into consideration data
distribution. Therfore, some clusters might be empty,
while others are overcrowded.
After the custering stage, we assigned the centers
of the clusters to the Neurosolver’s nodes.
Subsequently, for each data point we activated the
node that represented the cluster to which the point
was classified. The predicted sequences were built
also out of the numbers that corresponded to the
centers of the clusters represented by the firing
nodes.
FORECASTING WITH NEUROSOLVER
387

Figure 2: An example of data clustering.
4 NEUROSOLVER LEARNING
4.1 Learning Rules
We used two types of learning in our experiments.
The first follows the traditional incremental learning
through gradient ascent (a.k.a gradient descent and
hill-climbing) approaches (e.g., Russell, 2003) that
are taken by many researchers in the neural
networks community. The second, follows the
stochastic scheme that was used in the original
Neurosolver.
4.1.1 Incremental Learning
The Neurosolver learns by translating teaching
samples representing state transitions into sequences
of firing nodes corresponding to subsequent states in
the samples. For each state transition, two
connections are strengthened: one, in the direction of
the transition, between the lower divisions of the two
nodes, and another, in the opposite direction,
between the upper divisions as shown in Figure 3.
In the incremental learning, we simply add a small
value to the connection strength.
4.1.2 Statistical Learning
In the second approach, the strength of all inter-
nodal connections is computed as a function of two
probabilities: the probability that a firing source
node will generate an action potential in this
particular connection and the probability that the
target node will fire upon receiving an action
potential from the connection.
To compute the probabilities, each division and
each connection collects statistics as shown in
Figure 4. The number of transmissions of an action
potential T
out
is recorded for each connection. The
Figure 3: Neurosolver learning rule.
Figure 4: Statistics collected for computation of the
connection strength between nodes.
total number of cases when a division positively
influenced other nodes S
out
is collected for each
division. A positive influence means that an action
potential sent from a division of a firing node to
another node caused that node to fire in the next
cycle. In addition, we also collect statistical data that
relate to incoming signals. T
in
is the number of times
when an action potential transmitted over the
IJCCI 2009 - International Joint Conference on Computational Intelligence
388

Figure 5: The Neurosolver learn temporal patterns.
connection contributed to the firing of the target
node and is collected for each connection. S
in
,
collected for each division, is the total number of
times when any node positively influenced the node.
With such statistical data, we can calculate the
probability that an incoming action potential will
indeed cause the target node to fire. The final
formula that is used for computing the strength of a
connection (shown in Equation 1) is the likelihood
that a firing source node will induce an action
potential in the outgoing connection, multiplied by
the likelihood that the target node will fire due to an
incoming signal from the connection:
P = P
out
ڄP
in
= (T
out
/S
out
)ڄ(T
in
/ S
in
)
(1)
4.2 Learning Sequences
As we already indicated, in the goal-oriented
problem solving mode the function of the network of
upper divisions is to spread the search activity along
upper-to-upper connections. In the forecasting mode,
this network can be used to provide some guidance
in forecasting as we indicate in the notes on the
future directions of research. However, in the
experiments that we report in this paper, the network
of the upper divisions is ignored.
The purpose of the network composed of lower
divisions and their connections is to generate a
sequence of output signals from firing nodes (along
the connections shown in Figure 5). In the goal-
oriented search mode, such a sequence corresponds
to a path between the current state and the goal state,
and—as stated before—can be considered a solution
to the problem.
In the forecasting mode, the node corresponding
to the current state is activated through the thalamic
input and allowed to fire. The activity from the firing
node is transmitted to the nodes that are connected to
the firing node through the efferent connections with
non-zero strengths. Assuming substantial learning
sample, it is very likely that there is only one
connection that is strongest, so the node that is
connected through that connection is the winner of
the contest for the highest activation level. The
number that is the center of the cluster
corresponding to that node is the predicted vale. In
non-clustering tests, it is the datum that is associated
with the node. Subsequently, the winning node is
allowed to fire next, and the process for selecting the
winner is repeated until no more predictions can be
made.
4.3 Implementation Tweaks
4.3.1 Inhibition
As indicated earlier, to avoid oscillations, the firing
node is inhibited for a number of computation
cycles. The length of the inhibition determines the
length of cycles that can be prevented.
4.3.2 Higher-order Connections
Our initial implementation had first degree
connections that link only to a direct predecessor of
a node. We later enhanced our models with second
degree connections, which provided a link to more
distant predecessors in the Neurosolver’s firing
history. Adding connection degrees allows us to take
into consideration a number of previously fired
FORECASTING WITH NEUROSOLVER
389
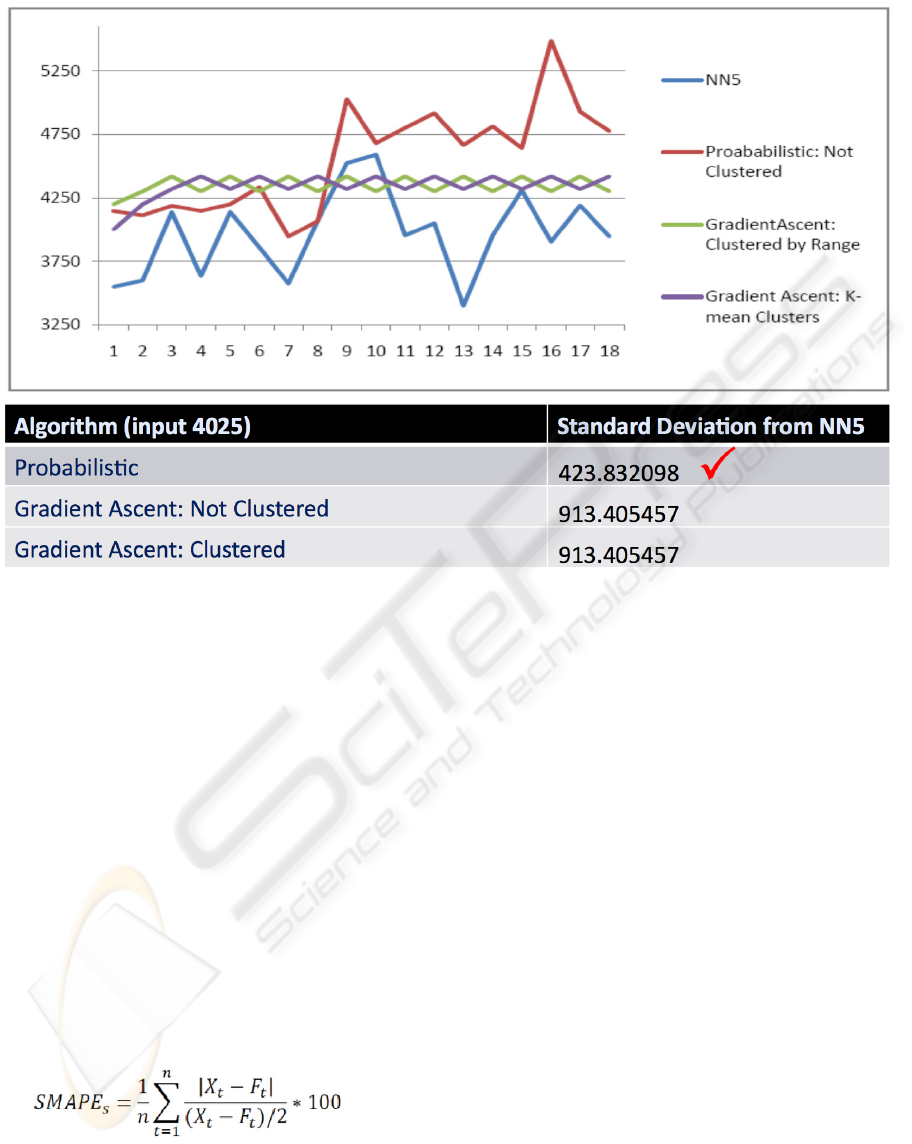
Figure 6: Probabilistic vs. Gradient Ascent.
nodes when forecasting the next node to fire. In that
respect, this approach is similar to Markov Models
(Markov, 2006).
5 EXPERIMENTS
5.1 Quality Measure
To measure the quality of our predictions and to
compare them with the benchmarks and submissions
to the NN5 competition we used Symmetric Mean
Absolute Percent Error (SMAPE) that was
recommended by the NN5 organizers. The SMAPE
calculates the symmetric absolute error in percent
between the actuals X and the forecast F across all
observations t of the test set of size n for each time
series s with the following formula:
(2)
5.2 Results
We generated a substantial body of results running
the NN5 data sets with numerous incarnations of the
Neurosolver. We processed the data in the raw form,
as well as pre-processed by clustering techniques as
described earlier. We also tested the Nuerosolver
with the two learning algorithm: gradient ascent and
stochastic.
In the following sections, we present an analysis
of the Neurosolver’s performance on some selected
data. In the analysis, we compare several models and
approaches that we used, and relate the results to the
test data provided with the NN5 data sets. We
conclude with a comparison with the benchmark
predictions generated by non-neural methods
provided by the organisers of the NN5 competition
for reference [NN5].
5.2.1 Comparing Learning Models
The graph in Figure 6 illustrates Neurosolver’s
predictions following presentation of one of the data
points (4025) from the NN5 data sets. The four lines
in the graph represent:
the actual data provided by the NN5
competition (drawn in blue),
our forecasted values for the stochastic model
(in red), and
forecasting made with two hill-climbing
models (in green and purple).
IJCCI 2009 - International Joint Conference on Computational Intelligence
390
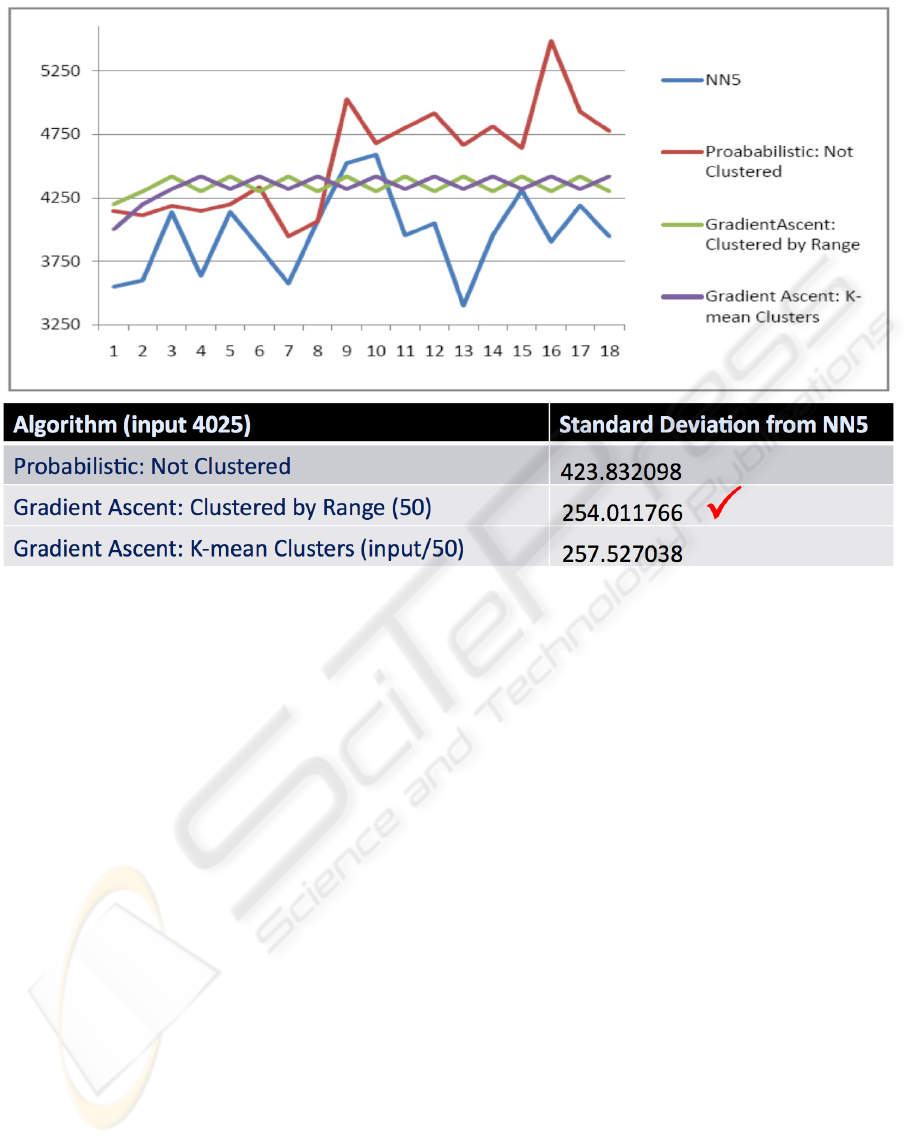
Figure 7: Clustered vs. Unclustered.
The data in the table below the graph show the
standard deviation between our results and the test
data from the NN5 data sets.
The graph in Figure 6, illustrates how the
Neurosolver behaves when the data is not shaped by
clustering algorithms. We used a cluster size of one
in the shown clustered gradient ascent, so a node is
used per each value, making it virtually the same as
an un-clustered model. Therefore, the Neurosolver
generated the same forecasts for both the clustered
and un-clustered gradient ascent models. The lines
corresponding to the two gradient ascent models—
drawn in purple and green—are collapsed and
displayed as a single purple line.
From the graph and the standard deviation
between the forecasted values and the NN5 data
(given in the table below the graph), we observe that
the probabilistic model provides forecasts that are
closer to the actual data (as provided with the NN5
sets) in terms of the standard deviation from the
measured data.
5.2.2 The Clustering Factor
The graph in Figure 7 illustrates how the clustering
algorithms affect the forecasting. The value used as
the input to our forecaster is the same as before
(4025). The cluster-by-range gradient ascent model
divides the input into 50 clusters. The k-means
clustering algorithm divides the size of the input by
50, giving us 173 clusters for this particular data set.
The significance of the clustering process can be
seen in the change in our standard deviation for the
gradient ascent model. The forecasted values from
the gradient ascent models are now much closer to
the actual data provided with the NN5 data sets.
The clustering algorithms provide an overall
improvement in our results; however, we have
encountered some cases in which the clustering
algorithm increased our deviation from the actual
values.
5.2.3 Comparing with the NN5 Submissions
The NN5 website provides a list of contest
submissions and benchmark results. They use the
SMAPE formula to calculate the quality of
predictions generated by the competing and
benchmark models. The best predictions that come
from benchmark models are shown on the right side
of Figure 8. No competing submission exceeded the
performance of the benchmark models.
The left side of Figure 8 shows the performance
of several models of the Neurosolver.
FORECASTING WITH NEUROSOLVER
391

Figure 8: Neurosolver vs. Benchmarks.
6 CONCLUSIONS
Currently our results are below the benchmarks on
the NN5 website. However, we are not that much
apart. We have found our current findings to be
promising and plan to amply a number of
improvements that we believe will improve the
performance of the Neurosolver significantly.
We plan to further investigate and compare our
results with other data sets. We are also looking
forward toward participating in the future NNx
competitions. As of this writing, a new competition
has not been announced.
We have concluded that a potential source for
our deviation in forecasted values could be due to
incomplete data in our learning set. In such cases the
Neurosolver gets stuck. We will be looking into
providing some means to boost Neurosolver’s
activity to address such problems.
As we indicated, we use node inhibition to solve
the problem with cycles that can lead to looping. At
the same time, however, we may prevent generation
of genuine cycles that may be present in the data.
We believe that this is the main cause of the
Neurosolver’s inability to generate predictions at
some points. We are planning to look into
developing a mechanism that would accommodate
generating genuine cycles while preventing endless
loops.
The improvement to our predictions after adding
second order connections was significant; therefore,
we expect that even higher-degree connections will
improve the results even further. However, higher-
degree connections are also computationally
expensive, so we will need to strike a balance
between the improvement to the prediction
capabilities and the efficiency of computations.
ACKNOWLEDGEMENTS
The author would like to express gratitude to several
students that were members of the research group
operating in Spring 2009 semester under the
umbrella of Faculty-Undergraduate Student
Research Initiative supported by California State
University Channel Islands. The following students
provided great help with programming, testing,
analyzing data and charting the results: Fahimeh
Fakour, Douglas Holmes, Maximillian Kaufmann,
and Nicholas Peters.
REFERENCES
Bieszczad, A. and Pagurek, B., 1998. Neurosolver:
Neuromorphic General Problem Solver, Information
Sciences: An International Journal 105, pp. 239-277,
Elsevier North-Holland, New York, NY..
Bieszczad, A., 2008. Exploring Neurosolver’s Forecasting
Capabilities, Proceedings of the 28th International
Symposium on Forecasting, Nice, France, June 22-25.
IJCCI 2009 - International Joint Conference on Computational Intelligence
392

Newell, A. and Simon, H. A., 1963. GPS: A program that
simulates human thought, in Feigenbaum, E. A. and
Feldman, J. (Eds.), Computer and Thought. New
York, NJ: McGrawHill.
Burnod, Y., 1988. An Adaptive Neural Network: The
Cerebral Cortex, Paris, France: Masson.
Laird, J. E., Newell, A. and Rosenbloom, P. S., 1987.
SOAR: An architecture for General Intelligence,
Artificial Intelligence, 33: 1--64.
Nillson, N. J., 1980. Principles of Artificial Intelligence,
Palo Alto, CA: Tioga Publishing Company.
Collins, Allan M.; Loftus, Elizabeth F., 1975. A
spreading-activation theory of semantic processing,
Psychological Review. Vol 82(6) 407-428.
Anderson, J. R., 1983. A spreading activation theory of
memory. Journal of Verbal Learning and Verbal
Behavior, 22, 261-295.
Markov, A. A., 2006. An Example of Statistical
Investigation of the Text Eugene Onegin Concerning
the Connection of Samples in Chains, translation. by
David Link. Science in Context 19.4: 591-600.
Russell, Stuart J.; Norvig, Peter (2003), Artificial
Intelligence: A Modern Approach (2nd ed.), Upper
Saddle River, NJ: Prentice Hall, pp. 111-114
NN5: http://www.neural-forecasting-competition.com/
FORECASTING WITH NEUROSOLVER
393
