
A COMPUTATIONAL STUDY OF THE DIFFUSE
NEIGHBOURHOODS IN BIOLOGICAL AND ARTIFICIAL
NEURAL NETWORKS
P. Fernández López, C. P. Suárez Araujo
Institute for Cybernetics, University of Las Palmas de Gran Canaria, Spain
P. García Báez
Dept. of Statistics, Operations Research and Computation, University of La Laguna, Spain
Keywords: Nitric oxide, Artificial neural networks, Cellular signalling, Volume transmission, Diffuse neighbourhood.
Abstract: This paper presents a computational study on a fundamental aspect concerning with the dynamic of nitric
oxide (NO) both in the biological and artificial neural networks, the Diffuse Neighbourhood (DNB). We
apply the compartmental model of NO diffusion as formal tool, using a computational neuroscience point of
view. The main objective is the analysis of DNB by the observation of the AI-NOD and CDNB variables,
defined in this work. We present a study of influences and dependences with respect to associated features
to the NO synthesis-diffusion process, and to the environment where it spreads (non-isotropy and non-
homogeneity). It is structured into three sets of experiences which cover the quoted aspects: influence of the
NO synthesis process, isolated and multiple processes, influence of distance to the element where NO is
synthesized, influence of features of the diffusion environment. The developments have been performed in
mono and bi-dimensional environments, with endothelial cell features. The importance of this study is
providing the needed formalism to quantify the information representation capacity that a type of NO
diffusion-based signalling presents and their implications in many other underlying neural mechanisms as
neural recruitment, synchronization of computations between neurons and in the brain activity in general.
1 INTRODUCTION
The understanding of brain structure and function
and its computational style is one of the biggest
challenges both in Neuroscience and Neural
Computation. To reach this aim it is essential to
know underlying mechanisms of the brain activity.
The activity of the brain has as principal
responsible the BNN, the cellular communication
and learning. Neural recruitment, or synchronization
of computations between neurons, the existence of
an information indexing schema at the Biological
Neural Network (BNN), or the LTP expression, are
aspects that can depend in a direct way on an
underlying neural signalling schema. We understand
that such aspects will be able to have a considerable
role in the information representation capacity, and
so, in the BNN and ANN computation potential.
Among all set of cellular signals that affect
globally the brain activity, the volume transmission
(VT) is located. Its underlying mechanism is the
diffusion of neuroactive substances and diffusible
signals, like Nitric Oxide (NO). NO is one of the
liposoluble molecules generated by cells from the
own tissue which allow a volumetric transmission. A
key property of NO is its extreme diffusibility in
both aqueous and lipid environments, which allows
a fast three-dimensional spread of the signal
irrespective of the presence of membranes (Suárez
Araujo, 2000). Because of this, it freely diffuses
through membranes affecting all neighbouring cells
(Hawkins, et al., 1993), (Schuman, et al., 1994),
(Zhuo, et al., 1998) and (Garthwaite, et al., 1995).
The presence of a molecule in the brain such as
NO, opens new perspectives in the study of the brain
functioning. NO can help as an element of control
for several systems. It can act as a retrograde
neurotransmitter; it can be involved in learning and
490
Fernández López P., P. Suárez Araujo C. and García Báez P. (2009).
A COMPUTATIONAL STUDY OF THE DIFFUSE NEIGHBOURHOODS IN BIOLOGICAL AND ARTIFICIAL NEURAL NETWORKS.
In Proceedings of the International Joint Conference on Computational Intelligence, pages 490-495
DOI: 10.5220/0002326004900495
Copyright
c
SciTePress

memory, and in the LTP process. It is capable to
produce hybrid neuromodulation, diffusive hybrid
neuromodulation (DHN) (Suárez Araujo, 2000). NO
has also opened a new dimension in our concept of
neural communication, overlaying the classical
synaptic neurotransmission, where information is
passed between neuronal elements at discrete loci
(synapses).
An intrinsic feature of the NO diffusion is the
formation of not-wired neighbourhoods, diffuse
neighbourhoods (DNB), which supports the
emerging of complex structures. The formation of
these structures has been a subject studied by other
authors (Krekelberg, 1996, 1997) and (Krekelberg
and Taylor, 1998). These studies have been specific
studies concerning with the cortical map formation
and their relationship with neighbourhoods in the
Kohonen SOM. They have not considered the DNB
as a possible underlying communication schema in
BNN and ANN. Our studies consider this capacity.
Our work introduces and studies fundamental
concepts in the formation of DNB, product of the
dynamics of NO diffusion. We understand DNB as
an auto-contained element in the behavior of NO
and the study of its dynamics as essential,
independent from the learning model or the neural
architecture where it is embodied in. This will
provide us a better understanding of the
computational skills that NO has; computational
skills based on the neural recruitment mechanisms,
emergence of complex structures and increase of
information capacity and processing. This justifies
the need of a generalist and in-depth development
like the one our work presents. We provide concepts
located in the Theoretical Framework of the study of
NO (Suárez Araujo, 2000). It will be able to manage
studies of causal aspects of the NO dynamics, and
comparative studies with concepts and classical
architectures.
In this paper, we focus our effort on the analysis
of DNB dynamics and its possible influence in
mechanisms and processes at the neural circuit
and/or higher level. An important aim is to infer
from the analysis a possible implication of VT in the
increase of the information representation capacity
in both BNN and ANN, in their architectures and in
the functional complexity of its main computation
element, the neuron.
We present a computational analysis of DNB,
based on our compartmental model of diffusion of
NO (Suárez Araujo, et al., 2006). This work requires
of a set of own concepts of the diffusive phenomena,
which we have defined and that are: Directionality
of NO dynamics (DNO), Average Influence (AI),
Diffusion Centre of the DNB (CDN) and DNB Limit
(DNBL).
The importance of this study is providing the
needed formalism to quantify the information
representation capacity that a type of NO diffusion-
based signalling can present.
2 METHOD
Diffusion is the main axis in the study of the NO
dynamics (Wood and Garthwaite, 1994), as well as
the main responsible of the NO influence to different
brain zones from a functional and structural point of
view. This influence is materialized, essentially, by
means of the Diffuse Neighbourhoods (DNB). This
concept allows to analyze how NO influences move
by means of diffusion as well as what is their
dependence with non-isotropy and non-
homogeneity. The establishment and analysis of
DNB, which we will perform using the
compartmental model of NO diffusion, precise to
formalize intrinsic aspects to the diffusion
phenomena and to the NO dynamics. On one hand,
we have the directionality measure of the NO
dynamics, which provokes different spatial-temporal
influences in the diffusion environment. This takes
us towards the concept of Average NO Influence,
key variable in the DNB definition. On the other
hand, its dynamic, adaptive and no local character
justifies the need of variables which formalize that
dynamism and its effect as diffusion centre of the
DNB and DNB limit.
2.1 Compartmental Model of NO
Diffusion and Concepts of Diffusion
The compartmental model of NO diffusion (Suárez
Araujo, et al., 2006) is a discrete computational
model that allows us to study the dynamic of NO,
generation, diffusion, self-regulation and
recombination, in biological and artificial
environments. Its main feature is its simplicity, it
can be considered as a general formal tool with
biological plausibility. It gathers real features of the
diffusion environment such as the no homogeneity
and the no-isotropy and possible morphology of the
NO synthesis.
It represents an important tool for designing and
interpreting biological experiments on NO behaviour
and its effect on brain structure and function.
The model is based in compartmental systems
(Anderson, 1983) and it is defined by a system of
A COMPUTATIONAL STUDY OF THE DIFFUSE NEIGHBOURHOODS IN BIOLOGICAL AND ARTIFICIAL
NEURAL NETWORKS
491

first order differential equations, like eq. (1), where
we can consider specific cyclic contour conditions.
dC
i
dt
=D
i,i−1
(C
i−1
−C
i
)+D
i,i+1
(C
i+1
−C
i
)−
λ
i
C
i
+F
i
(1)
Where D
i,i-1
and D
i,i+1
are the coefficients of
diffusion between the compartments i and i-1 and
between i and i+1, respectively. λ
i
is the self-
regulation parameter of NO. It is being considered,
for this case, a self-regulation of NO dynamics
proportional to the quantity of concentration, and F
i
is the function of generation of NO.
The computational analysis of DNB, using this
model requires of a set of own concepts of the
diffusion phenomena, which will be defined and that
are: Directionality of NO dynamics (DNO), Average
Influence (AI), Diffusion Centre of the DNB (CDN)
and DNB Limit (DNBL).
NO Directionality, (NOD)
NOD allows to assign an i state to every
compartment, associated to the movement that NO
has along each dimension. Basing on this, it can be
measured the permanence time of compartment i, in
such state, and to calculate the Average NO
Influence that a source i compartment can be
causing on a destination compartment j.
NOD is formally defined for an i compartment
by equation 2. Its value is function of the NO
concentration dynamics associated to the adjacent
compartments, according to the propagation schema
defined for each dimension.
()
()
()
1
1
22,1
112,1,1
,1,1
112,1,1
22,1
−
+
−−−
−−−−−
−+
+++++
+++
−
+
−
+++
−+
++−
=
i
i
iii
iiiiii
iiiii
iiiiii
iii
i
F
F
CD
CDD
CDD
CDD
CD
dt
dG
λ
λ
(2)
Basing on the NOD value in each dimension, an
i compartment can be located on 3, 9 or 27 states, for
environments with one, two or three dimensions,
respectively, Table 1.
Basing on time proportion, over the total time of
the diffusion process in which compartments are
located in one state, it can be calculated the Average
Influence that an i compartment is performing into
another j compartment.
Table 1: Possible states of a compartment in mono-
dimensional environments and its NOD values.
State G
i
Condition
←
G
i
< 0
→
G
i
> 0
↔
G
i
= 0
Average Influence (AI)
Average Influence between compartments by the
NO dynamics (AI) is a magnitude that quantifies the
influence k compartment is performing into r
compartment.
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
∏
∈ (...))),,,(,,,(
,,max),,(
TrqpTrpkTi
T
tEitrkI
ψ
(3)
Where i is every compartment that is located on
T(k, p, r, T(p, q, r, T(…))), path, definition-recursive,
which goes from k compartment to r compartment,
passing by intermediate compartment p and using
path T(p, q, r, T(…)). The function 0 <
ψ
(i, E
T
,t) < 1
defines the time proportion, over the total process
time t, that i compartment is located on the E
T
state
in favor of the direction followed that path T defines.
This magnitude is computed for a determined
instant, being able to vary throughout time.
Diffuse Neighbourhood (DNB)
Diffuse Neighbourhood (DNB) of an i compartment,
(4), is constituted by a set of compartments which
fulfill certain criteria with relation to the AI i
compartment is performing in them.
(
)
(
)
{
}
tjiIQjtV
i
,,:)(
=
(4)
Where Q(I(i, j, t)) is the Q criteria over the AI
that i compartment performs in the j one, and j
represents every compartment that fulfills Q. Q can
be the exceed of a threshold value
θ
by the AI. This
way, j
∈
V
i
(t)
⇔
Q(I(i, j, t)) is fulfilled, where Q is
defined according to the logical expression I(i, j, t) >
θ
. Another criterion could be that AI is located
between two values,
θ
1
y
θ
2
. So Q criterion would be
defined by the logical expression
θ
1
< I(i, j, t) <
θ
2
.
The way in which Q criterion is defined causes
different types of neighbourhoods, and the DNB of a
compartment can change throughout time. This way,
the DNB is dynamic and adaptive that generates
complex structures. These aspects of the DNB can
be featured by tracing the diffusion centres of every
instance of the DNB throughout time. This diffusion
centre of the DNB (CDNB) determines a position,
which corresponds to the averaged position of all the
IJCCI 2009 - International Joint Conference on Computational Intelligence
492
influences that compartments belonging to the
neighbourhood perform between them
∑∑
∈∈
=
ii
VjVj
ji
tjiItjiItV ),,(),,(),( rC
(5)
Where r
j
corresponds to the position j
compartment has in the diffusion media.
Diffuse Neighbourhood Limit, (DNBL)
We define Diffuse Neighbourhood Limit (DNBL) of
an i compartment as the max(|r
j
-r
i
|), where r
i
is the
position vector of the i compartment, r
j
is the
position vector associated to the j compartment, and
such compartment corresponds to any of the
compartments belonging to the DNB of the i
compartment i,j
∈
V
i
(t).
3 RESULTS AND DISCUSSION
We have performed a computational study of NO
dynamics, using the compartmental model of NO
diffusion by the observation of the AI-NOD and
CDNB variables.
We have focused our efforts in the analysis of
one of the great potentialities of NO as diffusive
signalling, the emergency of DNB and so, of
complex structures. We have established influences
and dependences with respect to associated features
to the NO synthesis-diffusion process, and to the
environment where it spreads (non-isotropy and no-
homogeneity) (Syková, 2001). We have structured
the study into three sets of experiences which cover
the quoted aspects: influence of the NO synthesis
process, isolated and multiple processes, influence
of distance to the element where NO is synthesized,
influence of features of the diffusion environment,
isotropy and homogeneity, presenting our obtained
results in this section.
The first two studies have been performed in a
mono-dimensional environment, figure 1, with
endothelial cell features. The values of the diffusion
and auto-regulation constants are, respectively, D =
3,3·103
μ
m
2
s
-1
and
λ
= 1,3863 s
-1
and average life
t
½
=0.5s. (Malinski, et al., 1993)
Figure 1: Environment of 401 compartments. The
synthesis processes are in the compartment 201 for
synthesis alone, and at 101, 201 and 301 for multiple
syntheses.
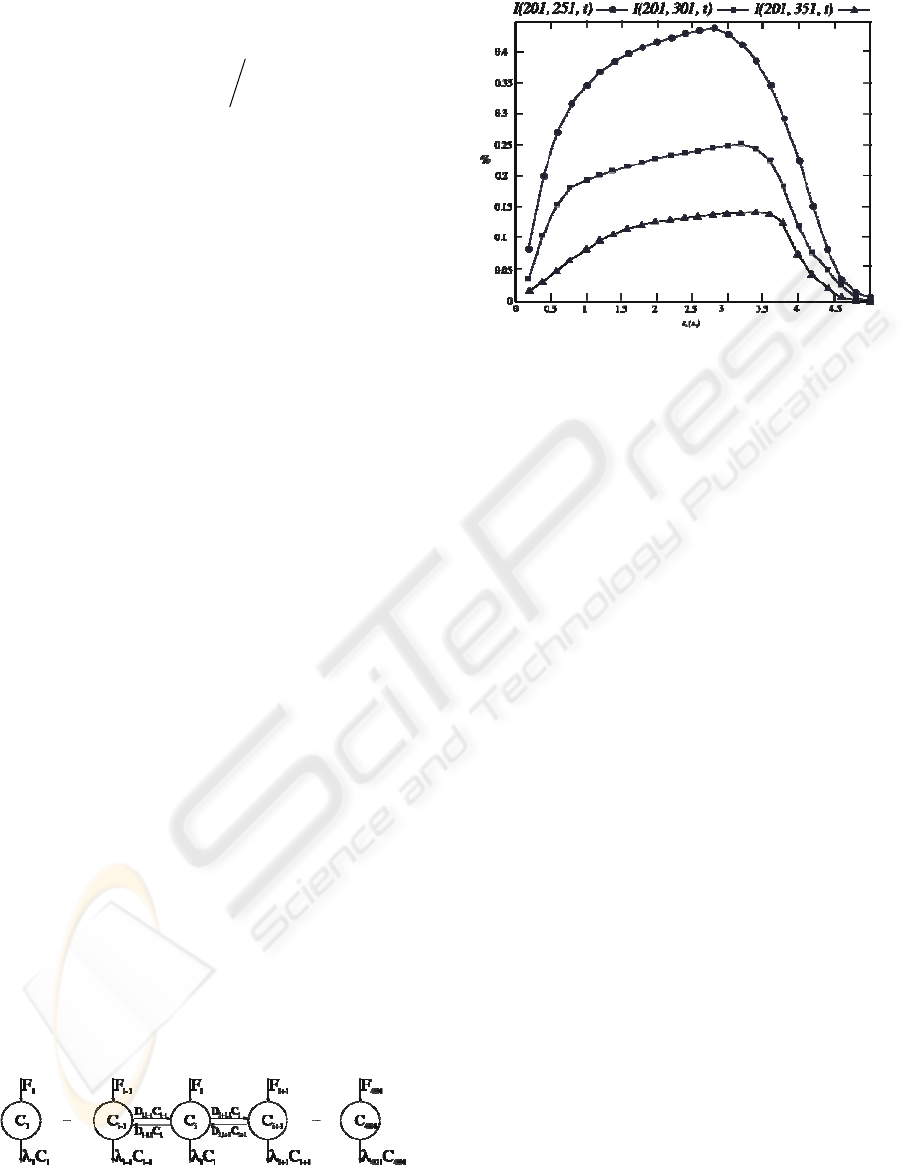
Figure 2: I(201, 251, t), I(201, 301, t), I(201, 351, t) AI
Profiles that compartment 201 produces into
compartments 251, 301, 351.
Figure 2 shows the AI which exerts the
compartment 201 into compartments placed at
different distances from it. It is observed the AI
dependence with the distance to the NO-generator
compartment and time. The synthesis process at
compartment 201 starts at t = 0 s., takes 0.2 s. and
presents trapezoidal morphology (Suárez, et al.,
2006). We have observed that I(201, 251, t) gets its
maximum, I
max
(201,251,t)
≅ 45%, at t ≅ 2.75 s.
Initially, compartments produce influence into other
compartments, in a fast way, the more the less
distance. This is fundamental to propitiate neural
recruitment processes, computations
synchronizations, adaptations to changes of
environment. Thus, when synthesis is over, there
already exists an AI greater than 15% of I
max
(201,
251, t). After reaching its maximum, I(201, 251, t)
decays at a faster speed, getting at t = 5 s., negligible
values. I(201, 301, t) takes a 25% more than I(201,
251, t) in reaching the maximum, and I(201, 351, t)
a 30% more, being the max influences much lower
in these compartments. When increasing the distance
in 50µm, the max AI value falls in a 50%, and when
increasing it in 50 µm. more, I
max
decreases a 75%,
Figure 1. This analysis takes us to another concept
as “the importance of neighbourhood” is threshold
value of I which compartments have to reach to
consider them as belonging to a DNB. Thus, DNB
are dynamic and adaptive, being formed gradually in
time by means of the incorporation of compartments
and, at the same time, modifying their order at the
neighbourhood. Importance will be an indicator of
the generated DNB stability; the more stable the
DNB, the lower its importance. This changing
character of DNB handles working in non-stationary
environments, real environments. It can help the
A COMPUTATIONAL STUDY OF THE DIFFUSE NEIGHBOURHOODS IN BIOLOGICAL AND ARTIFICIAL
NEURAL NETWORKS
493
formation of cortical maps (Krekelberg, 1996) and
(Krekelberg and Taylor, 1998), hybrid complex
structures, DNB + wired neighbourhoods, as well as
the incorporation of volume learning into BNN and
ANN.
All these computation and/or information
representation potentialities will be more justified
with the emergence of complexity in DNB when we
increase complexity in NO generation processes.
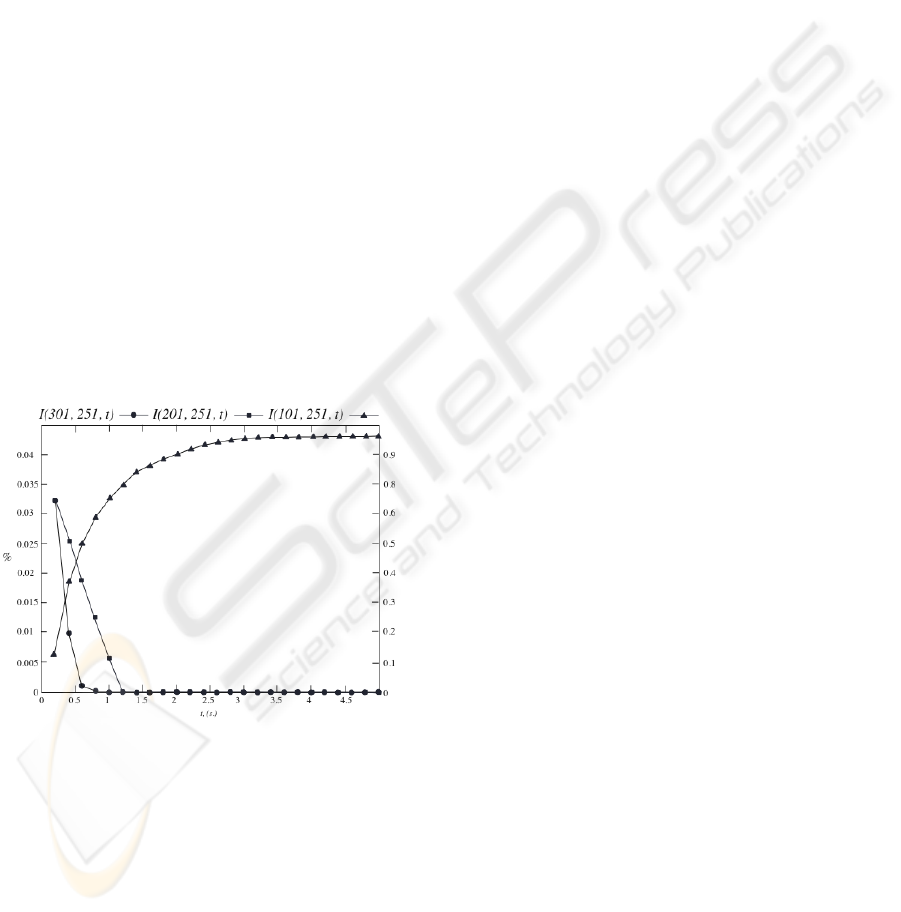
We have studied the dynamics in an environment
where there coexist several simultaneous synthesis
processes. We analyzed the AI in compartment 251,
when synthesis process exists in two symmetrical
positions to 251 at both sides. We have observed a
dynamics where compartments with minimum
influence exist. I(201, 251, t) as well as I(301, 251,
t) are lower than 3,5%, Figure 3. Thus, a value of
importance higher than this 3,5% implies this
compartment does not belong to both
neighbourhoods, even though it is at short distance
from the NO generation. It can be understood that
compartment 251 plays an isolator role of the
several complex structures that are formed. This
feature can indicate the existence of isolation zones
in the biological level, which can cause
computational segmentation and information
indexing.
Figure 3: I(201, 251, t), I(301, 251, t), I(101, 251, t) AI
Profiles that compartments 201 and 301 exert into
compartment 251, and compartment 101 into compartment
251, when there exist two, and three, simultaneous
synthesis processes, respectively.
It has been performed the study of the IM-NOD
profiles throughout time, when 3 simultaneous NO
synthesis processes exist, separated by 100
μ
m. one
another (compartments 101, 201 and 301).
Analyzing the IM-MOD compartment 101 exerts
into compartment 251, it is observed the additive
character that multiple and aligned generation
causes, Figure 3. To thwart this effect, it becomes
necessary the variability of the average NO lifetime
in the neural tissue. This is one of the biological
phenomena which can justify the environment non-
homogeneity.
Finally, it is shown the dependence that DNB
dynamics and CDNB have to environment non-
isotropy and non-homogeneity. We have worked in
a bi-dimensional environment with very low values
of the diffusion constant in two zones, which makes
the NO dynamics to be almost null. The diffusion
constant is in the range 3,3·10
3
± 0,2·10
3
μ
m
2
s
-1
in
the rest of the environment. There are induced two
NO synthesis processes in two compartments i, k. It
is observed a formation of non-symmetrical and
non-local DNB
i
and DNB
k
at times t = 0,6 s. and t=
1,3 s., Figures 4a and 4b. Thus it is noticed a
changing trajectory in CDNB and its possible
dependence in the way DNB does. For t = 0,6 s., in
both neighbourhoods, CDNB matches with the
compartment where synthesis was caused; however
for t = 1,3 s. in V
i
the position of CDNB has
changed, moving in agreement to that
neighbourhood shape.
4 CONCLUSIONS
We present a work developed from a computational
neuroscience point of view which provides a step
forward in the understanding of the VT and their
implications in the biological and artificial neural
networks.
We have performed a computational analysis of
one of the great potentialities of NO as diffusive
signalling, the DNB. We have used the
compartmental model of NO diffusion,
showing its
high capacity to study the dynamics of NO.
We have proposed and defined concepts
associated to the diffusion phenomena which present
significant capabilities to characterize the NO
dynamics. These concepts are Directionality of NO
dynamics, Average Influence, Importance of the
Neighborhood, Diffusion Centre of the DNB and
DNB Limit.
We have established that the generation and
dynamical behavior of the DNB depend on
associated characteristics to the NO synthesis-
diffusion processes, and to the environment where it
spreads (non-isotropy and non-homogeneity). The
complexity in DNB emerges when the complexity in
NO generation processes is increased. In this paper,
it is also showed the existence of isolation zones in
the biological level, which can cause computational
IJCCI 2009 - International Joint Conference on Computational Intelligence
494

a)
b)
Figure 4: Snapshot of the formation of two
neighbourhoods, DNB
i
, DNB
k
and position of CDNB
(indicated by a circle) in different times. Non-isotropic
and non-homogeneity environment of 16x16
compartaments. Black zone corresponds to null NO
dynamics. a) t = 0,6 s., b) t = 1,3 s.
segmentation and information indexing, and the
possibility to generate non local and non symmetric
DNB. With this study, it is possible to explain some
important environment features like the non-
homogeneity. Finally, all these results allow us to
detect the implications of VT, by means of DNB, in
the increasing of information representation
capacity, in the neural recruitment, in the
synchronization of computations between neurons,
in the neural modulation, in both scenarios,
biological and artificial. These implications will also
allow confirming the possible role of the NO on
several neural circuits as the sleep-wake cycle
control.
We will go onto these analysis about behavior of
DNB, developing complementary studies as
complex systems using bifurcation theory and
analysis.
REFERENCES
Suárez Araujo, C.P, 2000. Study on the Functional and
Organizational Role of the Neuromessenger Nitric
Oxide in Learning: An Artificial and Biological
Approach. In American Institute of Physics Press, Vol.
517, pp: 296-307
Suárez Araujo, C.P;, Fernández López P.; García Báez P.
and Simoes da Fonseca J.L., 2006. A Model of Nitric
Oxide Diffusion Based in Compartmental Systems.
In International Journal of Computing Anticipatory
Systems (IJCAS), Vol. 18, pp:172-186.
Hawkins, R.D., Kandel, E.R. and Siegelbaum, S.A., 1993.
In Annu. ev. Neurosci. 16, 625-665.
Schuman, E.M. and Madison D.V., 1994. Nitric Oxide and
Synaptic Function. In Annu. Rev. Neurosci. 17:153-
183.
Zhuo, M., Laitinen, J.T., Li, X.C. And Hawkins, R.D.,
1998. In Learn. Mem., 5, 467-480.
Garthwaite, J. and Boulton, C.L., 1995. Nitric Oxide
Signalling in the Central Nervous System. In Annu.
Rev. Physiol. 57 pp. 683-706.
Krekelberg, B., 1996. Nitric oxide in cortical map
formation. In Journal of Chemical Neuroanatomy, 10,
pp: 191-196.
Krekelberg, B., 1997. Modelling cortical seft-orgnization
by volumen learning. Doctoral Dissertation. King's
College London.
Krekelberg, B. and Taylor, J.G., 1998. A Dynamic
Neighbourhood Function in Volume Learning. In
Proceedings of the sixth annual conference on
Computational neuroscience : trends in research,
1998: trends in research, 1998, pp 71-76.
Wood, J. and Garthwaite, J., 1994. Models of the
Diffusional Spread of Nitric Oxide: Implications for
Neural Nitric Oxide Signalling and its
Pharmacological Properties. In Neuropharmacology
Vol. 33, N. 11, pp. 1235-1244.
Anderson, D.H., 1983. Compartmental analysis and tracer
kinetics. In Springer-Verlag, Berlin.
Syková, E., 2004. Extrasynaptic Volume Transmission
and Diffusion Parameters of the Extracellular Space.
In Neuroscience 129, pp 861-876.
Malinski, T. Taha Z., Grunfeld, S, Patton, S., Kapturczak,
M. and Tombouliant, P., 1993. Difusion of nitric oxide
in the aorta wall monitored in situ by porphyrinic
microsensors. In Biochem Biophys Res Commun, 193,
1076-1082.
A COMPUTATIONAL STUDY OF THE DIFFUSE NEIGHBOURHOODS IN BIOLOGICAL AND ARTIFICIAL
NEURAL NETWORKS
495
