
AN ARTIFICIAL MOLECULAR MODEL TO FOSTER
COMMUNITIES
Christoph Schommer
Department of Computer Science, University Luxembourg, 6 Coudenhove-Kalergi, 1359 Luxembourg, Luxembourg
Keywords:
Bio-inspired modeling, Graph mining, Bibliographic communities.
Abstract:
This paper introduces in extracts a bio-inspired model that understands graphs as artificial chemical constructs.
The main objective is to identify this model as an autonomous and adaptive system that performs internal
tasks, for example a communication with its environment. The model itself focus on artificial atomicity
of nodes, artificial molecular connections in between, and functional proteins, which are self-concentrated
constructs. The model implicates a solid fundament, but fosters an artificial vitality through catalysts: these
merge attacked atomic nodes – in case of common “interests” (inside the molecular model) – to functional
proteins and therefore consequently contribute to a vivid shape of communities. As an application example,
the theoretical model is clarified with bibliographic entries to form bibliographic communities dynamically
while having a bibliographic stream entries as input.
1 A SHAPE OF MOLECULES
Given an actor node, which represents a node within
a network, then we call this node atomic (α
A
i
) in a
sense that it is not divisible. Additionally, each node
α
A
i
shares an activation σ
A
i
and owns a set of items
Γ
A
i
(which will be described later on). An associa-
tion between two actor nodes A
i
and A
j
is then rep-
resented by a molecular bond, which describes a di-
rected relationship on a lower level. Each set of items
Γ
A
i
contains atomic entities, which exist in form of a
hierarchy.
sBond(α
A
i
,α
A
j
) =
ω
A
i
→A
j
: α
A
j
→ α
A
i
∨
α
A
i
→ α
A
j
0 : else
(1)
A single molecular bond has a weight of ω
A
i
→A
j
,
which is expressed by the conditional probability
P(A
j
—A
i
). If the relationship between the two actor
nodes is directed in both directions, then we call this
bi-relationship a double molecular bond:
dBond(α
A
i
,α
A
j
) =
ω
A
i
→A
j
× ω
A
j
→A
i
: α
A
j
→ α
A
i
∧
α
A
i
→ α
A
j
0 : else
(2)
The relationship is then characterized by the com-
mon connection weight ω
A
i
,A
j
, which is the product of
the individual values. Both atomic actor nodes share
an activation as well (σ
A
i
, σ
A
j
). With respect to this,
both structures then own a molecular structure in be-
tween, meaning that any combination of an atomic
structure results in a molecule. Such a molecule might
be of different granularity and size, and being expres-
sive in respect to its arity. As presented in Figure 1, a
single molecular bonds (left) and a double molecular
bonds (right) is shown (each consisting of two atomic
actor nucleus).
Figure 1: Single molecular bonds (top) and double molecu-
lar bonds (bottom) between two atomic actor nucleus.
With Γ
A
i
, we allow each actor to own a number of
items, for example interests that are organized within
a hierarchical system. We then receive levels of dif-
ferent granularity with for example γ
0
= {Root}, γ
1
=
{A,...,Z}, γ
2
= {A
1
,...,Z
n
}, and γ
3
= {A
1
,...,Z
nm
},
etc. The concept is that each time a association is per-
formed, the actor’s interest γ
j
A
i
may be extended by
another interest. The crucial idea is that interests may
be substituted by the superordinate hierarchy γ
j−1
A
i
in
case that a minimum number of interests (= min
k
γ
) on
the specified level exists:
219
Schommer C. (2009).
AN ARTIFICIAL MOLECULAR MODEL TO FOSTER COMMUNITIES.
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval, pages 219-222
DOI: 10.5220/0002326902190222
Copyright
c
SciTePress

γ
j
A
i
→ γ
j−1
A
i
(3)
if |(γ
j−1
A
i
| ≥ min
k
γ
for an actor node A
i
. For example, if
an actor A
i
is interested in γ
j
A
i
= {A
11
,A
12
,A
13
,A
14
},
then the interest level may be replaced to γ
j−1
A
i
= {A
1
}
in case that the threshold min
k
γ
is achieved.
a) b)
c) d)
Figure 2: Selected molecular forms with a) a molecular star,
b) a collection of molecular bridges (diamond), c) a molec-
ular bridge with single/double molecular bonds (bottom),
and d) a collection of diamonds.
Some examples of molecule structures are shown
in Figure 2. In Figure 2a), an atomic node α
A
i
is
shown, which is being arranged as a centre of k ad-
jacent nodes. We call this unary structure a molecule
star, because a certain number of actor nodes are
exclusively connected by a single, but centric actor
node:
mStar(α
A
i
) =
1 : 6 ∃sbond(α
A
j
,α
A
x
)∧
(
V
sBond(α
A
i
,α
A
j
)∨
V
dBond(α
A
i
,α
A
j
))
0 : else
(4)
∀1 ≤ j ≤ k with i /∈ {1,...,k} and x ∈ N. With
that, the situation inside a molecular star is that each
non-centric actor is only associated with the centric
actor node. The connection is generally a single bond,
either from the centric actor node α
A
i
to each neigh-
bors α
A
j
or vice versa. In case that two actor nodes
α
A
i
and α
A
j
share a double molecular bond, we call
this a molecular bridge. The molecule structure is of
a binary type since exactly two atomic nodes are in-
volved (Figure 2b) and Figure 2c)).
mBridge(α
A
i
,α
A
j
) = dBond(α
A
i
,α
A
j
) (5)
Besides, atomic actor nodes may play a role in-
side each molecule, being either a node that actively
stimulates another or a node that is passively stimu-
lated by another node, for example atomic triggers
and atomic reactors (Figure 1a)). A decomposition
of a molecule concerning a semantic assignment may
then be as follows: let α
A
i
, α
A
j
and α
A
k
disjunctive
atomic actor nodes, 1 ≤ i 6= j 6= k ≤ n natural num-
bers, and n the total number of nodes, then an atomic
actor node α
A
i
is a atomic reactor:
mReactor(α
A
i
) = ∃α
A
j
: sBond(α
A
j
,α
A
i
) (6)
On the other hand, an atomic actor node α
A
i
is an
atomic trigger:
mTrigger(α
A
i
) = ∃α
A
j
: sBond(α
A
i
,α
A
j
) (7)
An actor node α
A
i
is a atomic trigger if it influ-
ences another actor α
A
j
(α
A
i
⇒ α
A
j
) with ω
A
i
→A
j
ex-
ceeding min
ω
. An actor node α
A
i
is a atomic reactor
if α
A
i
is influenced by another actor α
A
j
(α
A
j
⇒ α
A
i
)
with with ω
A
j
→A
i
exceeding min
ω
. Third, we may de-
scribe an actor node α
A
i
as a atomic center if it is the
central point inside a molecular star.
There exist operational functions that are applica-
ble to relationships inside the molecules from a prac-
tical point of view. A first measure is the distance be-
tween two actor nodes d(α
A
i
, α
A
j
), which leads to us
the shortest path problem from α
A
i
to α
A
j
. But while
passing inner actor nodes, the distance, however, must
be influenced by the corresponding activation states
σ
A
i
as well. We therefore propose a distance measure
that sums up all actor node activities being on the the
shortest path from α
A
i
to α
A
j
. Since we can not guar-
antee that an actor node A
j
can be reached from actor
node A
i
and as we do not know if all participating ac-
tor nodes share at least a single molecular bond with
its successor, we suggest
d(α
A
i
,α
A
j
) =
∑
j
k=i
σ
A
k
: A
i
→ A
j
unde f ined : else
(8)
Depending on the relationship, the strength
s(α
A
i
,...α
A
j
of a relationship must be calculated in
a different way. For example, a molecular star is cer-
tainly depending on the number of associated actor
nodes α
A
j
, their activation states σ
A
j
, and the connec-
tion weights ω
A
i
→A
j
and ω
A
j
→A
i
, respectively, among
them:
s
mStar
(α
A
1
,...α
A
n
) =
n
∏
k,l=1
ω
A
k
→A
l
(9)
with k < l. For molecular bridges, however, the
“harmony” between the double bonds justifies a
stronger bridge (than a bridge with more varying sin-
gle bonds). The more harmonic a double bonds is the
stronger the bridge is.
s
mBridge
(α
A
i
,α
A
j
) = ω
A
i
→A
j
× ω
A
j
→A
i
(10)
with k < l.
KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval
220
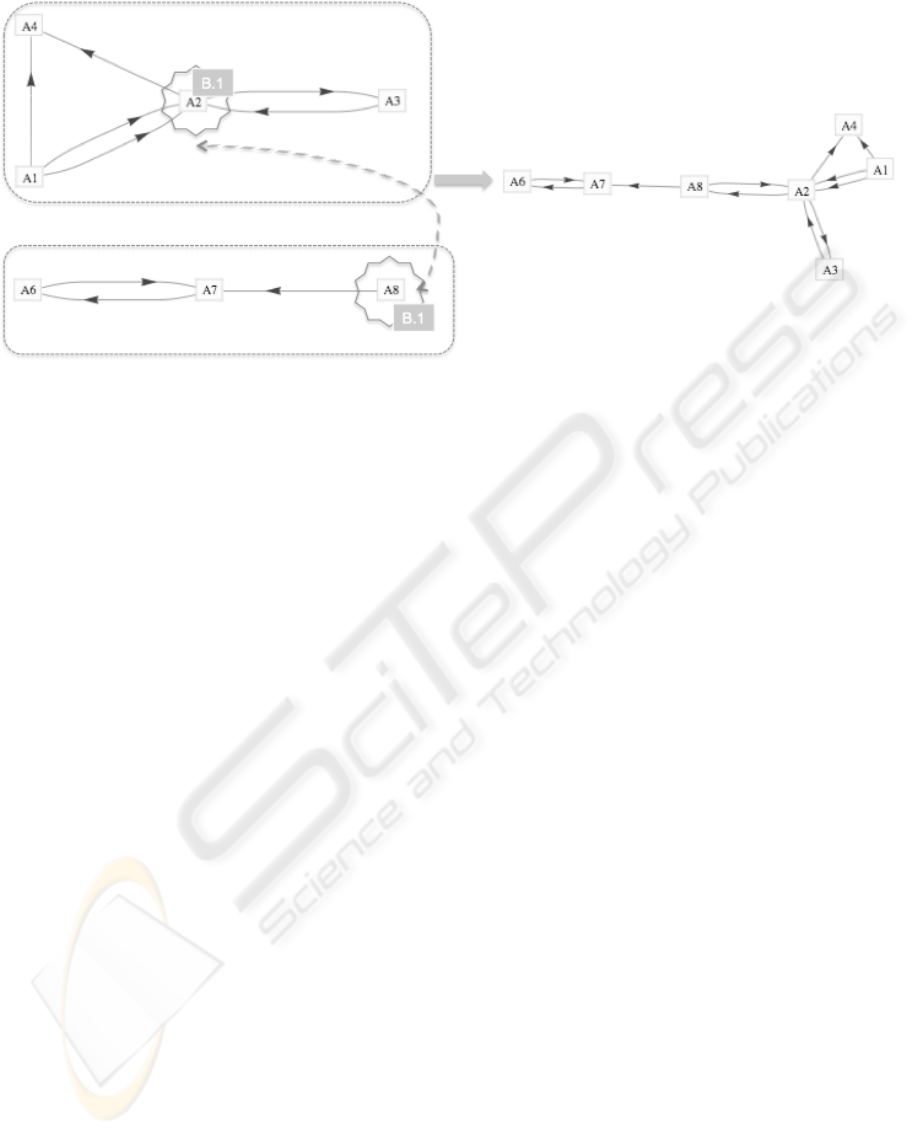
Figure 3: Reaction of two independent molecules to a functional protein. The merge is initiated by a catalyst τ that forms a
catalytic bridge between α
A
2
and α
A
8
. The merge evolves because of a common interest B
1
: in this case, it is an identical
classification chapter within the ACM classification system.
2 CATALYTIC BRIDGES
So far, the described molecular model stands for a
static description of the theory of graph. Therefore,
to overcome such a static molecular existence, we ex-
tend our model by taking advantage of the set of items
Γ
A
i
for each α
A
i
. It is interesting that each atomic ac-
tor node is allowed to react with another α
A
j
through
a catalyst τ: in case that an actor node α
A
i
with a set
of items ξ
i
owns the same or a subset of interests than
another actor node α
A
j
, then both may react, merge
and establish a catalytic bridge τ
A
i
,A
j
(Figure 3).
A functional protein Π
k
is therefore unlike a static
collection of nodes but moreover a vivid (artificial)
and autonomous system. Besides, we understand
these functional proteins as an operating structure that
is commissioned to complete tasks: it is conceivable
to send information and to describe the structure it
obsesses. Functional proteins may be forced to con-
tinuously improve its own structure: such an improve-
ment may be the update of existing single or double
bonds or atomic nodes (decrease/increase).
3 AN APPLICATION EXAMPLE
In case of bibliographic networks, the existence of
molecular stars and bridges leads to a more detailed
characterization of an author (node); for example, a
protein may (autonomously) inform about experts –
who form a central part (node) within a molecular
star – inside a community and/or about noticeable
actor/co-authorships through molecular bridges. A
functional protein may therefore autonomously (and
independently) send information to its environment,
for example to natural users while providing them
with information about the existence of “interests”
and/or the structure of the associated community (re-
trieve). With the mentioned semantic roles of an ac-
tor, the activity of the protein – and with it the com-
munity as well – can be measured. The more active
atomic trigger exist, the more active the community
generally will be. On the other side, a more reactive
community exists if the number of reactor nodes are
lower.
If actor atomic author nodes are interconnected by
a catalytic bridge, then they substantiate a common
interest. For example, this may occur with respect
to common research topics, possibly identified by the
ACM classification system. In any case, a merge be-
tween author nodes foster a dynamic-adaptive net-
work behavior, because novel connections between
actor nodes may be established depending on their
“interest” and the bibliographic stream of incoming
publications.
As a consequence, a bibliographic community is
therefore not only a set of relationships among au-
thor nodes but consequently previously independent
molecules by a catalytic bridge. So, we understand
bibliographic communities as mental systems that are
physically expressed by even such functional proteins
with relationships (author A
i
is associated to A
j
) and
semantic roles (A
i
is a trigger, A
j
the central point of a
star). These communities change over time while fig-
uring out the protein generation process in response
to a bibliographic stream, but will definitely operate
AN ARTIFICIAL MOLECULAR MODEL TO FOSTER COMMUNITIES
221

in a non-stream environment as well.
4 CONCLUSIONS
This position paper contains in extracts a bio-inspired
model, which follows the natural example of a molec-
ular world and which understands graph-related struc-
tures as molecular entities. The main objective is to
define a model that autonomously and adaptively be-
haves while performing internal tasks like the com-
munication with its environment, for example inside
communities. In this respect, fundamental compo-
nents like single/double bonds have been presented as
well as simple molecular shapes.
Currently, we are working on the stability of
atomic node, molecules, and proteins: a first approach
towards the stability of proteins is surely to count the
number of actor nodes at time points t and t − 1, re-
spectively, where we then get
∆(Π
i
,t) =
α
t
A
i
− α
t−1
A
i
α
t−1
A
i
(11)
The stability of a protein decreases, if ∆(Π
i
,t) ≤
0; it increases, if ∆(Π
i
,t) > 0. Even better, the corre-
sponding activity weights ω
A
i
→A
j
of the bonds and the
activation state of the atomic actor node σ
A
i
shall be
taken into account. However, the question concerning
the stability of molecular bonds and atomic actors is
herewith not answered and we for example check up
if a “valency” can be simulated as well and if other
criteria may be taken to fulfill a merge between ac-
tor nodes: when a catalyst starts its activity, does it
make a difference to start with some actor node or is
it of interesting to distinguish between “begin” and
“end” actor nodes? Furthermore, the semantic roles
inside a protein surely plays a promising aspect to-
wards the stability, since if all actor nodes are satisfied
and “convivial” in some way then the stability surely
is stronger than in another situation. Another inter-
esting point is the communication of a protein with
its environment, respective with other proteins: how
can information smoothly addressed to all proteins?
Here, we are currently thinking on taking into account
achievements from other bio-inspired systems like ar-
tificial immune systems.
ACKNOWLEDGEMENTS
The work is currently been done at the MINE re-
search group of the ILIAS Laboratory, Department of
Computer Science and Communication, University of
Luxembourg.
REFERENCES
Cai, D., Shao, Z., Hen, X., Yan, X., and Han, J.
(2005). Community mining from multi-relational net-
works. In Lecture Notes in Computer Science Vol.
3721/2005. Springer.
Girvan, M. and Newman, M. E. J. (2002). Community
structure in social and biological networks. In Na-
tional Academy of Science USA, 99:8271-8276.
Inokuchi, A., Washio, T., Nishimura, K., and Motoda, H.
(2002). A fast algorithm for mining frequent con-
nected subgraphs. In IBM Research, Tokyo Research
Laboratory. IBM Press.
Leach, A. (2001). Molecular Modelling - Principles and
Applications. Prentice Hall, 2nd edition. Mika, P.
(2007). Social Networks and the Semantic Web.
Springer, 1st edition.
Schommer, C. (2008). Sieving publishing communities in
dblp. In ICDIM Third International Conference on
Digital Information Management. IEEE Computer
Society.
Yan, X. and Han, J. (2002). gspan: Graph-based substruc-
ture pattern mining. In IEEE International Conference
on Data Mining (ICDM 2002). I EEE Computer So-
ciety.
KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval
222
