UNBOXING DATA MINING VIA DECOMPOSITION IN OPERATORS

Towards Macro Optimization and Distribution

Alexander W¨ohrer

, Yan Zhang

1,2

, Ehtesam-ul-Haq Dar

and Peter Brezany

Institute of Scientiﬁc Computing, Faculty of Computer Science, University of Vienna

Nordbergstrasse 15/C/3, 1090 Vienna, Austria

School of Computer and Information Technology, Beijing Jiaotong University

Shangyuan Residence 3, Haidian District, Beijing 100044, China

Keywords:

Data mining operators, Macro optimization, Distributed data mining.

Abstract:

Data mining deals with ﬁnding hidden knowledge patterns in often huge data sets. The work presented in

this paper elaborates on deﬁning data mining tasks in terms of ﬁne-grained composable operators instead of

coarse-grained black box algorithms. Data mining tasks in the knowledge discovery process typically need

one relational table as input and data preprocessing and integration beforehand. The possible combination of

different kind of operators (relational, data mining and data preprocessing operators) represents a novel holistic

view on the knowledge discovery process. Initially, as described in this paper, for the low-level execution phase

but yielding the potential for rich optimization similar to relational query optimization. We argue that such

macro-optimization embracing the overall KDD process leads to improved performance instead of focusing

on just a small part of it via micro-optimization.

1 INTRODUCTION

The rapidly growing wealth, complexity and diversity

of data open many new opportunities in business, re-

search, design, policy formulation and decision mak-

ing. These opportunities will not be explored un-

less we advance the state of the art in data integra-

tion and analysis. The European project ADMIRE

(Advanced Data Mining and Integration Research for

Europe) (Atkinson et al., 2008) is pioneering archi-

tectures and models that will deliver a coherent, ex-

tensible and ﬂexible framework for data mining and

integration to make the best use of a wide range of

distributed data resources. Research in the area of re-

lational query processing pioneered the deﬁnition of

re-usable standard sub-components dividing the over-

all task into smaller pieces, so called relational op-

erators. First into logical ones and later into con-

crete physical ones, allowing advanced query opti-

mization (Ioannidis, 1996) and well elaborated cen-

tralized, distributed and parallel query execution ar-

chitectures (Kossmann, 2000). Many data mining al-

gorithms have similar behavior during, at least, an

important part of their execution too. This led us to

Presantaion Layer

OGSA-DQP

OGSA-DAI

Op5Op3

Op2

Op1

Op4

Data mining Operators

Relational Operators

Input

output

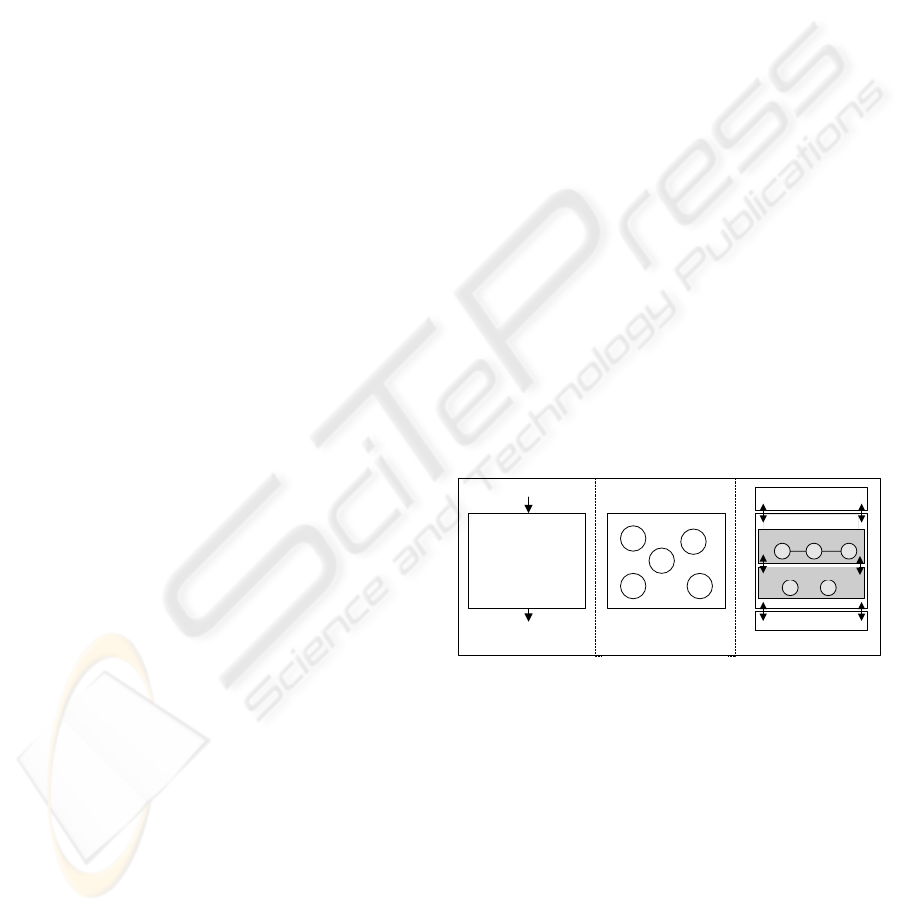
(a) (b) (c)

DM Algorithms

Figure 1: (a) Traditional black box DM algorithm imple-

mentation. (b) Composable operators. (c) Implementation

of a KDD process in OGSA-DQP.

consider to apply a similar operator-based approach

to decompose KDD processes in order to achieve re-

usability, ﬂexibility and extensibility.

This requires a transition from traditional black

box data mining algorithm implementation towards

re-usable operator based implementations as shown

in Figure 1. The current state-of-the art approach

is presented in Figure 1 (a) where the functionality

and intermediate steps of the used data mining algo-

rithm is hidden. The open source data mining toolkit

WEKA (Witten et al., 1999) is a well known repre-

243

Wöehrer A., Zhang Y., Dar E. and Brezany P. (2009).

UNBOXING DATA MINING VIA DECOMPOSITION IN OPERATORS - Towards Macro Optimization and Distribution.

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval, pages 243-248

DOI: 10.5220/0002333102430248

 SciTePress

sentative following this approach. Figure 1 (b) pic-

tures an arbitrary set of re-usable data mining oper-

ators needed to realize the functionality of one spe-

ciﬁc data mining algorithm. Figure 1 (c) presents a

high-level view of how we implemented the required

set of operators for a KDD process, in our case re-

quiring sequential pattern mining, by extending the

service-oriented distributed query processing engine

OGSA-DQP (Alpdemir et al., 2004) with ﬁne-grained

data mining operators. As data mining tasks in the

knowledge discovery process typically need one rela-

tional table as input and data preprocessing and inte-

gration beforehand, the possible combination of dif-

ferent kind of operators (relational, data mining and

data preprocessing operators) represents a novel way

of tight integration of data access, data integration and

data mining.

The rest of the paper is structured as follows. Sec-

tion 2 introduces needed background while Section

5 discusses related work. Section 3 elaborates on

data mining operators for sequential patterns and de-

scribes their proof of concept implementation via the

OGSA-DQP framework. Section 4 discusses macro

optimization of KDD process enabled by an operator

based view on it. Section 6 concludes the paper and

outlines future work.

2 BACKGROUND

Sequential Patterns were ﬁrst introduced in

(Agrawal and Srikant, 1995) and deals with the

extraction of knowledge which consists of frequently

occurring events or elements. Let us suppose that T =

,..I

} be the non empty set of items or events.

Then a sequence is an ordered list of items or events

which can be represented as S= hs

i,where s

an itemset. The order of itemsets depends upon time

or date. To extract the frequent sequences different

constrains are being deﬁned by the user. Sequential

pattern is a frequent pattern which satisﬁes the

minimum threshold frequency called support, deﬁned

support(S) =

Total occurrence of Sequence S in DB

Total number of transactions in DB

A sequence s is a maximal sequence if it is not

contain in any other sequence. To get the maximal

frequent sequence the non-maximal sequences have

to be eliminated.

Relational Operators are the building blocks of a

query tree representing some SQL statement to re-

trieve data. To perform its tasks operators typically

follow the iterator model (Graefe, 1993) which con-

sists of open, fetch-next, and close methods. The

open-function allocates memory for an operator’s in-

put(s) and output while fetch-next retrieves all the tu-

ples iteratively from its child operators and process

them according to the task of the operator. When

all input tuples have been processed and related out-

put was generated the close-function is called to de-

allocate the resources which were allocated during

processing. The operators can be divided into two cat-

egories, blocking and non-blocking query operators.

• blocking: An operator which produces output

only when it goes through all the input tuples ﬁrst.

An example for a blocking relational operator is

the group-by operator.

• non-blocking: Such operators produce the output

without reading all the available input tuples. An

example for a non-blocking relational operator is

the select operator.

OGSA-DQP (Alpdemir et al., 2004) is a ser-

vice based framework capable of performing dis-

tributed query processing over OGSA-DAI (Antonio-

letti et al., 2005) data services and other Web services

on the Grid. OGSA-DAI is a de-facto standard mid-

dleware to access databases on the Grid. The OGSA-

DQP coordinator service produces a query plan from

the user query. This query is translated into differ-

ent query partitions which are being executed by the

evaluator services.

The process of relational query optimization

and its components is pictured in Figure 2. The sin-

Query

Parser

Execution

Engine

Optimizer

Logical

Single-node

Physical

Partitioner

Scheduler

Multi-node

Figure 2: Components of relational query optimization and

processing.

gle node optimizer produces a query plan as it would

run on one processor. The parser transforms the query

into an internal logical representation which gets op-

timized by the logical optimizer. The physical op-

timizer transforms the logical expression into exe-

cutable physical query plans by selecting algorithms

that implement each of the operations in the logical

plan, e.g. hash join for a join operation. If multiple

processors are available, the multi node optimizer di-

vides the query plan into several partitions (by the par-

titioner) which are allocated to machine resources (by

the scheduler). Optimizations are typically based on

cardinality estimation, data distribution and knowl-

edge about the runtime behavior and requirements of

the operators (Ioannidis, 1996).

KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval

244

3 OPERATORS

The sequential pattern mining process is divided into

six logical operators. One of these six operators is a

common relational operator and ﬁve are speciﬁc data

mining operators to ﬁnd sequential patterns. The fol-

lowing sections elaborates on their deﬁnitions, rela-

tions and implementation.

3.1 Deﬁnition

SeqTableScan η Operator. This common relational

operator retrieves all the tuples from a data source.

The deﬁnition of this operator is shown below:

T1 = η

(id,date,items)

(table)

The operator takes as argument the input table and tar-

get columns in it. The output of this operator consists

of a table with columns id, date and items. The op-

erator

sorts the input tuples according to id and date

respectively in ascending order.

Conversion ρ Operator. This operator is used to

create sequence per id. It receives its input tuples

from the SeqTableScan operator η and then clusters

the items having the same id and order them accord-

ing to date. The operator has the following deﬁnition:

T2 = ρ

id,sequence(items (1,....,n))

(T1)

As shown by the expression this operator takes T1 as

an input argument and the output consists of tuples

with id and sequence.

PowerSet σ Operator. The third operator receives it

input tuples from the Conversion operator ρ. The op-

erator works according to the mathematical principle

of Power Sets. This operator converts every sequence

of a id into its corresponding power sets. The operator

deﬁnition is shown below:

T3 = σ

id, ps sequence←ps(s

,....,s

)

(T2)

The output T3 consists of id and ps sequence. Here

ps sequence will be achieved by applying the ps oper-

ation to every sequence s

available in the ’sequence’

column of the input tuples from T2.

LargeItemSet γ Operator. The fourth operator re-

cieves its input tuples from the PowerSet operator

σ and then searches the large itemsets within them.

The large itemsets are those itemsets which satisfy

the minimum support threshold, another input argu-

ment provided by the user. It compares each of se-

quences related to one id with other sequences and

combines several needed relational operators into one.

This is done due the possibility to push-down the task to-

wards the RDBMS via an appropriate SQL statement like

’select ... from ... order by’

this comparison will give the total number of occur-

rences of a sequence of speciﬁc id. If that count

complies with the user provided support then that se-

quence will qualify for the large itemset while the

sequences which do not fulﬁll the minimum support

threshold will be eliminated. The operator is deﬁned

as follows:

T4 = γ

sequence,support

≥support

user

(T3)

Its output tuples consist of sequence and support.

SeqTableScan

ConversionPowerSet

LargeItemSet

Tranformation

MaximalSeq

Blocking operator

Non-blocking operator

Figure 3: Operator hierarchy.

Transformation β Operator. This operator retrieves

its input tuples from the LargeItemSet and Conversion

operator. The deﬁnition of this operator is given be-

low:

T5 = β

id,trans formed

(T4, T2)

With the help of these two inputs this operator

transforms the Customer Sequence to corresponding

Transformed Sequences. For this process two steps

are required:

1. Take the customer sequences received from Con-

version operator and replace them with the corre-

sponding power sets.

2. Using data retrieved from LargeItemSet elimi-

nates those sequences which do not satisfy the

minimum support threshold.

The output tuples of this operator consist of id and

transformed ﬁelds.

Maximal Sequence α Operator. This operator re-

quires tuples from two input operators, namely Tran-

formation and LargeItemSet and ﬁnds the maximal

sequences. The operator is deﬁned as follows:

T6 = α

max seq

(T4, T5)

UNBOXING DATA MINING VIA DECOMPOSITION IN OPERATORS - Towards Macro Optimization and Distribution

245

The output of this operator are the maximal sequential

patterns. The description of the operators, their rela-

tion and semantics result in the operator tree shown in

Figure 3.

3.2 Implementation

The OGSA-DQP evaluator - our implementation en-

vironment - follows the iterator model (Graefe, 1993).

To implement operators in this model each operator

has to implement three abstract methods. The code

example given in Listing 1 illustrates howthe operator

tree shown in Figure 3 is created inside OGSA-DQP.

Listing 1: Operator usage for sequential pattern mining.

SeqTableScan Op1=SeqTableScan("select ...from...")

Conversion Op2=Conversion(Op1 ,...)

PowerSet Op3=PowerSet(Op2 ,...)

LargeItemset Op4=LargeItemset(Op3,support ,...)

Transform Op5=Transform(Op2,Op4,...)

MaximalSeq Op6=MaximalSeq(Op4,Op5,support ,..)

Op6.open();

{

tuple = Op6.next()

(valid tuple) {

store or display retrieved tuple

}

while

(!EOF)

Op6.close();

To show the feasibility of our approach initial

performance results of our implementation are pre-

sented based on datasets from the UCI KDD Archive

(Hettich and Bay, 1999). They consist of 41,096,

77,285, 159,128, 316,969 records respectively. These

datasets are about the page visits of users who vis-

ited msnbc.com. The performance of each data min-

ing operator for all different datasets is being shown

in Figure 4.

10000

20000

30000

40000

50000

60000

70000

80000

C P L T M

Data mining Operators

Time in Miliseconds

DS-1(41,096) DS-2(77,285) DS-3(159,128) DS-4(316,969)

Figure 4: Operator performance with four different datasets.

4 MACRO OPTIMIZATION

An operator based logical description of a KDD pro-

cess will allow optimizations considering the overall

process structure, as pictured in Figure 5 below. We

call this envisioned process macro optimization, us-

ing knowledge about data statistics, the execution en-

vironment, operator characteristics and their require-

ments.

Data-Pre

Processing

Decision

Tree

Data

Integration

Data

Access

Data

Access

Query

DPP

host 1

host 2

Figure 5: Logical KDD process description vs. optimized

distributed physical execution plan.

In our example a decision tree on a distributed

data set requiring some preprocessing has to be con-

structed. The logical description follows the typical

subsequent phases of a KDD process. First data se-

lection (and integration in our case), then data prepa-

ration and later on the ultimate data mining. Now we

envision a similar optimization process on this inte-

grated KDD process than for relational query opti-

mization, pictured in Figure 2 and brieﬂy discussed

in Section 2. The logical optimizer applies similar

heuristics than in relational optimization, e.g. apply

data preprocessing as early as possible but at least be-

fore data mining operators instead of pushing-down

conditions as far as possible the relational query tree.

The physical optimizer uses data statistics, e.g. esti-

mated cardinalities of operators, tuples size, column

content, in order to choose the most appropriate im-

plementations of the required data preprocessing and

decision tree tasks. The multi-node optimizer knows

the available execution environment and recognizes

the initial data distribution. It replaces the intended

data integration operator, e.g. UNION or JOIN, with

a decision tree implementation supporting the given

horizontal or vertical tuple distribution and includes

required exchange (Graefe and Davison, 1993) op-

erators. Additionally, an operator based model en-

courages adaptivity during execution (Gounaris et al.,

2002).

KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval

246

5 RELATED WORK

According to (Johnson et al., 2000), research in data

mining can be classiﬁed broadly into two ”direc-

tions”. The ﬁrst has focused primarily on which kinds

of patterns to mine, and how fast they can be com-

puted. The second recognizes that mining would be

far more effective if not considered in isolation and

has focused on how mining can interact with other

”components” in a more general framework of knowl-

edge discovery. Our research is following the second

direction.

Different frameworks were proposed to support

the knowledge discovery in databases (KDD) pro-

cess in a uniform manner. (Geist and Sattler, 2004)

proposes one based on constraint database concepts

as well as interestingness values of patterns. The

overall KDD process is divided into three main

steps - namely pre-processing, data mining and post-

processing - and for each of these different operators

are being deﬁned and their implementation issues for

decision trees are being discussed. The 3W model and

algebra (Johnson et al., 2000) uses regions, dimen-

sions and hierarchies to deﬁne a uniform framework

and operators. The model consists of three worlds

(intensional, extensional and data world) and oper-

ators for moving in and out of the worlds and for

the intensional world are deﬁned. (Fernandez-Baizan

et al., 1998) outlines the design of a RDBMS that will

provide the user with traditional query capabilities as

well as KDD queries based on operators. Further re-

search on exploiting relational and inductive database

technology for data mining exists, e.g. (Botta et al.,

2004). In (Meo et al., 1996) a model is deﬁned

to extract association rules via an SQL-like operator

named ’MINE RULE’. (YUAN, 2003) uses data min-

ing operators approach to ﬁnd association rules using

nested relations from the database. For this purpose a

new query language with the name M2MQL is being

deﬁned and semantics of its relevant operator’s alge-

bra is being discussed.

The following two efforts support users in deﬁn-

ing data mining processes. The Intelligent Discov-

ery Assistant (IDA) (Bernstein et al., 2005) provides

users with systematic enumerations of valid data min-

ing processes and effective rankings of these valid

processes by different criteria, to facilitate the choice

of processes to execute. This is done via ontological

operator descriptions and heuristic ranking methods.

(Abe and Yamaguchi, 2004) describes constructive

meta-learning by recomposing methods into learn-

ing schemes with mining (inductive learning) method

repositories that come from decomposition of popular

mining algorithms. It constructs the learning scheme

proper to a given data set

The work described in this paper differs from the

research introduced above by the following features:

open: The concepts nor the implementation is bound

to a speciﬁc RDBMS.

holistic: The possible combination of different kind

of operators (relational, data mining, etc.) represents

a novel way of tight integration of so far sub-sequent

treated phases in the knowledge discovery process for

optimization as well as execution.

distributed/parallel: Distribution of input data as well

as of operators and parallel execution on different ma-

chines is anticipated and supported by our implemen-

tation environment and its underlying iterator model

already.

granularity: Our operators are typically much more

ﬁne grained in order to be re-used for data mining al-

gorithms sharing similar behavior.

logical vs. physical: A uniﬁed view on the KDD pro-

cess with different abstraction levels, e.g. logical op-

erator tree and its actual physical implementation, al-

lows for various optimization mechanisms.

6 CONCLUSIONS

The opportunities of the rapidly growing wealth,

complexity and diversity of data will not be explored

unless we advance the state of the art in data inte-

gration and analysis. Research in the area of rela-

tional query processing pioneered the deﬁnition of re-

usable standard sub-components dividing the overall

task into smaller pieces, so called relational opera-

tors. Many data mining algorithms have similar be-

havior during, at least, an important part of their ex-

ecution too. This led us to consider to apply a simi-

lar operator-based approach to decompose KDD pro-

cesses in order to achieve re-usability, ﬂexibility, ex-

tensibility and optimisation.

We introduced an operator based approach to ex-

tract sequential patterns by using relational and data

mining operators in combination. This represent a

transition from traditional black box data mining al-

gorithm implementation towards re-usable operator

based implementations. The deﬁned operators have

been implemented inside OGSA-DQP, showing the

feasibility of our approach.

Data mining tasks in the knowledge discovery

process typically need one relational table as input

and data preprocessing and integration beforehand.

The possible combination of different kind of oper-

ators (relational, data mining and data preprocess-

ing operators) represents a novel holistic view on the

knowledge discovery process. Initially for the low-

UNBOXING DATA MINING VIA DECOMPOSITION IN OPERATORS - Towards Macro Optimization and Distribution

247

level execution phase but yielding the potential for

rich macro optimization of the overall process simi-

lar to relational query optimization (logical, physical,

distributed/parallel).

Our future work plan includes the following: mi-

grating to the latest version of OGSA-DAI allow-

ing complex workﬂow graphs, applying the operator

based approach to our earlier work for distributed de-

cision trees (Hofer and Brezany, 2004), extending the

set of data mining operators to cover association rule

mining, and higher level optimization components for

KDD processes.

ACKNOWLEDGMENTS

This work has been supported by the ADMIRE

project which is ﬁnanced by the European Commis-

sion via Framework Program 7 through contract no.

FP7-ICT-215024. Yan Zhang has been supported by

Project No. 2006AA01A121 of the National High-

Tech. R&D Program of China.

REFERENCES

Abe, H. and Yamaguchi, T. (2004). Constructive meta-

learning with machine learning method repositories.

In IEA/AIE, pages 502–511.

Agrawal, R. and Srikant, R. (1995). Mining sequential pat-

terns. In ICDE, pages 3–14.

Alpdemir, N. M., Mukherjee, A., Gounaris, A., Paton,

N. W., Watson, P., Fernandes, A. A., and Fitzgerald,

D. J. (2004). Ogsa-dqp: A service for distributed

querying on the grid. In Advances in Database Tech-

nology - EDBT 2004, pages 858–861.

Antonioletti, M., Atkinson, M., Baxter, R., Borley, A.,

Hong, N. P. C., Collins, B., Hardman, N., Hume,

A., Knox, A., Jackson, M., Magowan, J., Paton, N.,

Pearson, D., Sugden, T., Watson, P., and Westhead,

M. (2005). The design and implementation of grid

database services in ogsa-dai. Concurrency and Com-

putation: Practice and Experience, 17:357–376.

Atkinson, M., Brezany, P., Corcho, O., Han, L., van

Hemert, J., Hluchy, L., Hume, A., Janciak, I., Krause,

A., Snelling, D., and W¨ohrer, A. (2008). Admire

white paper: Motivation, strategy, overview and im-

pact. http://www.admire-project.eu/docs/ADMIRE-

WhitePaper.pdf.

Bernstein, A., Provost, F., and Hill, S. (2005). Toward

intelligent assistance for a data mining process: An

ontology-based approach for cost-sensitive classiﬁca-

tion. IEEE Transactions on Knowledge and Data En-

gineering, 17(4):503–518.

Botta, M., Boulicaut, J.-F., Masson, C., and Meo, R. (2004).

Query languages supporting descriptive rule mining:

A comparative study. In Database Support for Data

Mining Applications, pages 24–51.

Fernandez-Baizan, M., Ruiz, E. M., Pena-Sanchez, J., and

Pastrana, B. (1998). integrating KDD algorithms and

RDBMS code. In Proceedings of RSCTC’98, pages

210–213.

Geist, I. and Sattler, K.-U. (2004). Towards data mining op-

erators in database systems: Algebra and implementa-

tion. Technical Report 124, University of Magdeburg.

Gounaris, A., Paton, N. W., Fernandes, A. A. A., and Sakel-

lariou, R. (2002). Adaptive query processing: A sur-

vey. In BNCOD, pages 11–25.

Graefe, G. (1993). Query evaluation techniques for large

databases. ACM Computing Surveys, 25(2):73–170.

Graefe, G. and Davison, D. (1993). Encapsulation of par-

allelism and architecture-independence in extensible

database query execution. IEEE Transactions on Soft-

ware Engineering, 19(8):749–764.

Hettich, S. and Bay, S. (1999). The UCI KDD Archive.

Hofer, J. and Brezany, P. (2004). Digidt: Distributed clas-

siﬁer construction in the grid data mining framework

gridminer-core. In In Proceedings of the Workshop

on Data Mining and the Grid (GM-Grid 2004) held in

conjunction with the 4th IEEE International Confer-

ence on Data Mining (ICDM’04).

Ioannidis, Y. E. (1996). Query optimization. ACM Comput-

ing Surveys, 28(1).

Johnson, T., Lakshmanan, L., and Ng, R. (2000). The 3w

model and algebra for uniﬁed data mining. In VLDB,

pages 21–32.

Kossmann, D. (2000). The state of the art in distributed

query processing. ACM Computing Surveys (CSUR),

32(4).

Meo, R., Psaila, G., and Ceri, S. (1996). A new sql-like

operator for mining association rules. In VLDB, pages

122–133.

Witten, I. H., Frank, E., Trigg, L., Hall, M., Holmes, G., and

Cunningham, S. J. (1999). Weka: Practical machine

learning tools and techniques with Java implementa-

tions. In Proceedings of the Workshop on Emerging

Knowledge Engineering and Connectionist-Based In-

formation Systems, pages 192–196.

YUAN, X. (2003). Data mining query language design and

implementation. Master’s thesis, The Chinese Univer-

sity of Hong Kong.

KDIR 2009 - International Conference on Knowledge Discovery and Information Retrieval

248