
A SIMPLE NEURAL-NETWORK ALGORITHM
FOR CLASSIFICATION OF LIDAR SIGNALS APPLIED
TO FOREST-FIRE DETECTION
Andrei B. Utkin, Alexander Lavrov
INOV - INESC Inovação, Rua Alves Redol, Lisbon, Portugal
Rui Vilar
DEMAT, Instituto Superior Técnico, Technical University of Lisbon, Lisbon, Portugal
Keywords: Perceptron, Lidar, Signal processing, Singular value decomposition, Radial-basis function networks.
Abstract: Detection of smoke plumes using lidar provides many advantages with respect to passive methods of fire
surveillance. However, the great sensitivity of the method results in the detection of many spurious signals.
Correspondingly, the automatic lidar surveillance must be provided with effective algorithms of separation
of the smoke-plume signatures from irrelevant signals. The paper discusses a simple and robust lidar pattern
recognition procedure based on the fast extraction of sufficiently pronounced signal peaks and their
classification with a perceptron, whose efficiency is enhanced by a fast nonlinear preprocessing. The
algorithm is benchmarked against previously developed artificial-intelligence methods of smoke recognition
via Relative Operating Characteristic (ROC curve) analysis.
1 INTRODUCTION
Extending the principles of radar to the optical
range, lidar (light detection and ranging) presents
significant advantages in comparison with passive
surveillance methods, in particular a higher
sensitivity and low dependency on light and weather
conditions. Lidar detectors provide a large range of
surveillance, restricted only by the laser-pulse
energy and — for distances exceeding ~10 km — by
the beam jitter resulted from atmospheric turbulence.
Good directionality and precision of distance
measurements enable lidar to provide an accurate
location of smoke plumes. For efficient early forest-
fire detection, the smoke-plume pattern in the lidar
signal (peak of the retroreflected power) must be
promptly recognized by an adequate automatic
procedure despite the presence of additional peaks
due to noise and other targets. The present paper
details the investigation of one such procedure based
on the fast localization of peaks whose amplitude is
sufficiently large to correspond to possible smoke-
plume signatures. These peaks are subjected to
feature extraction and highly nonlinear binarization
transformation, which increases the number of signal
components. The binarized patterns are then
classified with a single-layer perceptron.
Lidar equipment (Fig. 1) consists of a radiation
emitter (pulsed laser and beam-formation optics) and
a radiation receiver (usually comprising of a light
gathering optical train, photodetector and
preamplifier). The emitter produces short and
intense radiation pulses; a part of this radiation is
scattered backwards and collected by the receiver,
where its power is converted into an electric signal.
The electric signal is amplified and directed to the
data-acquisition unit, to be recorded in a digital form
as a function of time.
Figure 1: Lidar equipment and detection principles.
569
Utkin A., Lavrov A. and Vilar R. (2009).
A SIMPLE NEURAL-NETWORK ALGORITHM FOR CLASSIFICATION OF LIDAR SIGNALS APPLIED TO FOREST-FIRE DETECTION.
In Proceedings of the International Joint Conference on Computational Intelligence, pages 569-574
DOI: 10.5220/0002334305690574
Copyright
c
SciTePress

Lidars for automated surveillance are supplemented
with a signal recognition system, performing
classification of target signatures and issuing, if
needed, an alarm signal containing information
about the target that caused the alarm situation.
2 BASIC RELATIONS
The distance from the lidar to the target R may be
calculated from the time delay t between the laser-
pulse emission and the reception of the
backscattered signal,
cRt /2= , c is the velocity of
light. The raw lidar signal S is the receiver-unit
output voltage recorded during some period of time
immediately after the laser-pulse emission (
0
=
t ).
As far as the transition from the time to the distance
dependence is reduced to a simple rescaling, usually
the raw lidar signal is represented as a plot of S
versus the distance R rather than the time t:
() ( )
(
)
2/,
0
ctRSRGIRStS
ubph
=+=⇒
(1)
where G is the total electronic gain,
() ()
RPRI
rphubph
ξ
=
is the unbiased photodetector
current (
ph
ξ
is the photodetector responsivity and
r
P is the retroreflected radiation power) and
0
S is
the background component, accumulating all types
of electric displacement and low-frequency noise
that can be assumed to be constant during the
relatively short measurement time: about 67
μs for a
range of 10 km, according to relation (1).
A theoretical estimation of
r
P is given by the
lidar equation:
()
()
()
⎟
⎠
⎞
⎜
⎝
⎛
−=
∫
R
rectr
rec
lr
dRR
R
A
Rc
ERP
0
2
''2exp
2
αττ
β
(2)
where
l
E is the output laser pulse energy,
β
the
backscattering coefficient of the medium,
rec
A
the
effective receiver area,
tr
τ
and
rec
τ
the transmitter
and receiver efficiencies, and
α
the extinction
coefficient.
At the early stage of a fire, the characteristic
spread of the smoke plume in the direction of laser-
beam propagation
sp
RΔ
(Fig. 2) is about 10 m. To
be able to reveal specific few-meter scale structures
that make the smoke-plume signatures different
from other lidar returns, the data-acquisition unit
must measure the photodetector output with a
sampling interval
R
δ
~ 1.5 m, eventually yielding
the discrete-time lidar signal in the form
()()
(
)
()
,
2
,''2exp
0
0
0
2
0
constA
c
EGC
SdRR
R
R
CtRS
rectrreclph
R
==
+
⎟
⎠
⎞
⎜
⎝
⎛
−=
∫
ττξ
α
β
(3)
digitized at the points ,/2 cRt
ii
= ,RiR
i
δ
=
RRiii
δ
/,,,1,0
maxmaxmax
=
=
… .
Figure 2: The main spatial parameters of smoke-plume
detection.
According to (1) and (2), smoke plumes manifest
themselves in raw lidar signals as peaks whose
amplitude and shape vary due to the stochastic
changes in the particle distribution within the smoke
plume under the action of gas-dynamic forces,
buoyancy and wind. The smoke-plume signatures
are observed against a background contaminated by
electronic and atmospheric noise (Fig. 3). Electronic
noise of a well constructed receiver usually
demonstrates no dependence on the distance and can
be estimated from a signal segment recorded far
beyond the range of the instrument, where no signal
attributable to retroreflection is expected.
Figure 3: Composition of the raw lidar signal.
Apart from this unstructured noise, the lidar signal
may contain peaks due to retroreflection from hills,
trees, buildings, birds, etc. Solid-target signatures
R
sp
Δ
R
sp
δ
R
α
s
p
x
β
sp
0
S
sp
N
S
ϕ
ϑ
Smoke
plume
signature
Peaks due to atmospheric and
electronic noise
R, m
Lidar signal, a.u.
Irrelevant
target
R
sp
IJCCI 2009 - International Joint Conference on Computational Intelligence
570

are narrow pulse-like waveforms, since the
backscattering occurs at almost a single distance.
The shape of these peaks is mainly defined by the
bandwidth of the detection channel and the rate of
the analog-to-digital conversion.
3 RECOGNITION STRATEGY
3.1 Characterization
As seen from (3), the shape of the smoke-plume
signatures in the lidar signal depends in a
complicated way on the profiles of the extinction
and backscattering coefficients along the beam
propagation direction. Although important for
prediction of the lidar range, gas-dynamic smoke-
plume models do not provide a solid basis for the
extraction of the characteristic features of the
smoke-plume signature. Due to this lack of reliable
parametric models, automated fire surveillance is
mainly based on artificial-intelligence algorithms
such as neural network (NN) methods.
In principle, lidar identifies targets with the
precision of a few meters, thus allowing for a very
accurate location of the fire. The angular target
position (the azimuth
ϕ
and elevation
ϑ
, see Fig. 2)
is given by the laser beam direction, but the
calculation of the distance to the smoke plume R
sp
is
carried out by the signal analysis unit.
NN architectures and algorithms suited for lidar
data extraction have been discussed in the literature
since the 1990s (Bhattacharya et al., 1997). It was
established that waveforms containing small
retroreflection from distributed targets could not be
directly presented to a neural network. A simple and
fast preprocessing method was developed for
facilitating the recognition, ensuring, at the same
time, that the processed waveforms properly reflect
subtle variations in the original waveforms.
Following the same principles as the radial-basis
function algorithms (Bishop, 1995; Haykin, 1999),
the recognition efficiency of a perceptron-based NN
is enhanced by a special binarization procedure that
uses a 2D grid in the signal-distance plane for the
waveform representation and a point-to-node
proximity criterion for assigning one or zero to the
grid nodes. Each node is treated as a separate input
component, increasing the network input dimension,
number of adjustable weights and, according to
Cover's theorem (Haykin, 1999), improving pattern
separability.
3.2 Problems
The application in question is characterized by the
following difficulties:
1. The length of the discrete-time sequence to be
processed,
RRi
δ
/
maxmax
=
~6.7×10
3
, is much
larger than in other lidar applications, such as
underwater object detection (Mitra et al., 2003). As a
result, the conventional NN algorithms
(Bhattacharya et al., 1997; Mitra et al., 2003) cannot
be straightforwardly applied because they require
excessive computation time and resources. In
addition, fire may occur anywhere within the
surveillance range, so no narrower region of interest
can be selected a priori.
2. Smoke-plume signatures are compact. As seen
from Eq. (3), for a starting fire the characteristic
spread of a smoke-plume signature
ss
RΔ , within
which the backscattering factor
β
is sufficiently
large to produce the signal above the noise level, is
restricted by the spread of the plume:
10
≈
Δ
≤
Δ
spss
RR m. Well-developed fires result in
much wider plumes, but denser smoke increases the
laser-beam extinction up to the values
α
~ 0.2 m
–1
(Kozlov and Panchenko, 1996). In these
circumstances, the smoke-plume signature decreases
down to the noise level at distances of the order of
α
–1
due to the Beer-Lambert absorption of both the
laser beam and retroreflected light, resulting in
ss
R
Δ
~ 5 m. Measured as number of points in the
digitized signal,
RRN
ssss
δ
/
Δ
=
, the signature
spread is always much less than that for the cases
described by Bhattacharya et al. (1997) and Mitra et
al. (2003), typically consisting of 5-10 points. The
short signature width and the great variety of
possible waveforms impede application of statistics-
based algorithms for noise reduction and signal
compression, which effectively reduce the
computational load in many other applications
(Mitra et al., 2003).
3. The fact that the distance to the target R
sp
must
be determined during the recognition may
complicate the NN structure: for the straightforward
algorithms, it turns the multiple input - single output
classification scheme into one with multiple outputs,
in which the additional neurons codify, in an analog
or digital way, the value of R
sp.
4. Due to the fact that a constant background can
be represented as a sum of uniformly distributed
peaks, the problem of peak recognition is not
linearly separable a priory and cannot be solved
without introduction of preprocessing and/or non-
linearity.
A SIMPLE NEURAL-NETWORK ALGORITHM FOR CLASSIFICATION OF LIDAR SIGNALS APPLIED TO
FOREST-FIRE DETECTION
571
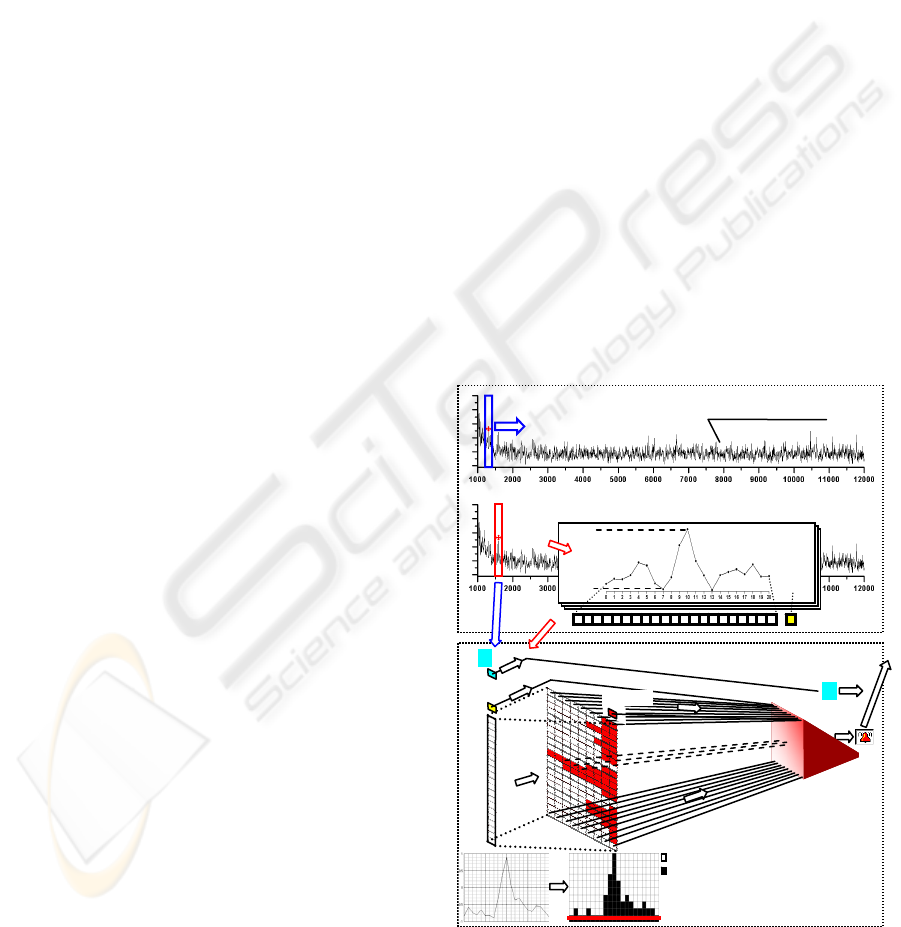
3.3 Knowledge and Invariances
According to general indications (Anderson, 1988),
to solve the problems presented in Sec. 3.2, a
specialized NN algorithm must be developed,
incorporating all prior information in order to
simplify the overall structure and facilitate the
recognition. Depending on its nature, the knowledge
about the input signal can be represented as a
transformation, selection rule and/or invariant and
then built into the system via specific design or
preprocessing procedures (Haykin, 1999).
The analysis of the lidar signal, briefly presented
in subsections 2.1, 2.2 and 3.2, makes it possible to
point out the following peculiarities:
1. The smoke-plume signatures manifest
themselves in the raw lidar signal as peaks whose
characteristic width
ss
RΔ (several meters) is much
less than the typical distance to the smoke plume R
sp
(from hundred meters to several kilometers).
2. The position of the smoke-signature maximum
corresponds to the desired distance to the smoke
plume.
3. The local noise level may be estimated as the
root-mean-square of the signal just before and after
the peak and the segment of the lidar signal of the
length ~
ss
RΔ3 , containing the smoke-signature
maximum in its center, is supposed to provide
information of both the smoke-signature shape and
the local noise. The ratio of the peak amplitude to
the mean local noise, called peak-to-noise ratio
(PNR), represents an important scale-independent
characteristic of the peak magnitude, closely linked
with the probability of the peak to be a target
signature rather than clutter. For this reason, it is
worthwhile to treat PNR as an invariant
characteristic feature to be extracted and presented
for recognition in a separate way.
Within the range
max
10 RRR
ss
≤≤Δ the shape
factor of the smoke-plume signature is invariant with
respect to the distance R (Utkin et al., 2009).
Obviously, the noise distorts the smoke-plume
signatures more at greater distances, and the pattern-
recognition problem in question can be treated as
distance-independent in the sense that the
recognition conditions for a tenuous smoke plume
are equivalent to those for a dense plume observed at
a greater distance provided that the signal-to-noise
ratio is the same.
3.4 Implementation
The knowledge and invariances are built into the
system via the following preprocessing procedure:
The raw lidar signal consisting of several thousand
points (
RRi
δ
/
maxmax
=
) is viewed by the
preprocessing software through a window of several
tens of points (
RR
ss
δ
/3~
Δ
) that moves along the
signal curve. The window motion stops if the local
signal maximum coincides with the window center
w
R and the corresponding peak-to-noise ratio
)(
w
RPNR is calculated. If
()
thrw
PNRRPNR < ,
where the threshold value
thr
PNR (typically, from 3
to 5) is chosen in accordance with the sensitivity of a
given lidar system, the peak is considered to be too
small for being a smoke-plume signature and the
observation window continues its motion along the
lidar-signal curve. Otherwise the signal pattern
within the window is sent to the recognition unit.
The corresponding feature value
)(
w
RPNR is
introduced directly to the NN through a special input
(Fig. 4).
Eventual alarm generation is performed on the
basis of pattern classification (smoke-signature
dichotomy) with a single-layer neural network
(perceptron), which is functionally equivalent to the
adaptive linear filter (Haykin, 1999).
Figure 4: Stages of the smoke-signature recognition
procedure.
PNR calculation
R
p
=1296 m
P
NR = 2.485
Pattern extraction
R
p
=1584 m
P
NR = 6.745
R
,
PNR
6.745
1
–
1
PNR
Threshold
binarization
Perceptron =
linear least-squares
filtering
Pattern recognition
R
p
R
p
Initial input: raw lidar signal
0
1
Bias +1
IJCCI 2009 - International Joint Conference on Computational Intelligence
572

Borrowing the approach from the radial-basis
function network theory (notably, it can be shown
that the binarization processing correspond to a
radial-basis function technique with some specific
norm), classification efficiency of the perceptron is
enhanced by nonlinear threshold binarization
transformation to higher dimensional space, similar
to Bhattacharya's processing of lidar signal
(Bhattacharya et al., 1997) for the detection of fish
in near-shore waters: The signal pattern is mapped
on a rectangular 2D grid. Each sample point is
checked against the grid-crossing points. If a sample
point falls within half a grid space on either side in
both the horizontal and vertical directions, a one is
assigned at that point; otherwise, a zero is assigned.
Each sample point is tested in the same way,
yielding at the end a matrix of zeros and ones,
eventually converted into a longer binary pattern
vector reflecting all the peculiarities of the pattern,
provided that a sufficiently fine grid is chosen.
When the vertical grid spacing equals the lidar
sampling distance so that all the signal points are
located on the vertical grid lines, the above
algorithm reduces to a simple point binarization of
the signal with resolution corresponding to the
horizontal grid spacing. The threshold binarization
procedure, corresponding to the point binarization in
which a one is assigned to each grid point situated
below any point already assigned to one, is even
easier for hardware implementation (a batch of
threshold detectors with linearly increasing
thresholds) and results in less sparse and more
compact binarized samples: the bottom line always
contains ones and can be discarded.
Notably, the number of binarization levels is a
free parameter of the recognition scheme.
Decreasing the number of levels, one can produce
rougher binary signal description and, at the same
time, reduce the signal dimension and the number of
adaptive parameters of the recognition process.
Being chosen on the basis of the bias-variance trade-
off (Haykin, 1999), the number of binarization levels
plays the same role as the number of training epochs
in the iterative learning rules.
The supervised learning procedure is implemented
through the least-squares filtering. For a given
training set, it readily yields a unique deterministic
solution (Haykin, 1999) for the desired
interconnection weights as a product of
pseudoinverse of the matrix composed from the
binarized training samples and the vector of
corresponding classification tags (here, 1 for the
smoke-signature peaks and –1 for the spurious signal
peaks).
Following Bishop's recommendations (Bishop,
1995), the instability arisen from the sparse nature of
the binary-sample matrices and incomplete ranks is
overcome by stabilized pseudoinversion on the basis
of singular-value decomposition (Press et al., 1986).
The binary input has two additional entries: one for
the constant activation bias (+1) and the other for the
PNR value that passes to the perceptron without
binarization. The alarm signal is accompanied by the
current position of the moving window center
spw
RR ≈
that corresponds to the maximum of the
retroreflected radiation and thus provides the desired
distance to detected smoke plume.
Figure 5: ROC curves corresponding to the developed
threshold-binarization algorithm and the three committee
machines described by Fernandes et al. (2004).
4 RESULTS
Fig. 5 illustrates comparison of the developed
threshold-binarization algorithm with three more
complicated artificial-intelligence methods
developed for smoke-signature recognition in the
lidar signal (Fernandes et al., 2004). The threshold-
binarization algorithm demonstrated superior
efficiency in the area of false alarm rate greater than
0.65%, resulting to 100% detection of the smoke
signatures in the validation set at the false alarm rate
as low as 0.84% (91 false detections at recognition
of 10891 noise peaks in 112 recorded lidar signals).
At the same time, the proposed algorithm:
yields nearly one order of magnitude faster
training;
the developed supervised learning procedure is
not connected with the choice of the best
classifier, so it can be strictly formalized and
performed by users without special instruction;
A SIMPLE NEURAL-NETWORK ALGORITHM FOR CLASSIFICATION OF LIDAR SIGNALS APPLIED TO
FOREST-FIRE DETECTION
573

the learning procedure is fast and of predictable
duration: it does not involve repetitive/iterative
routines like training epochs in the case of
gradient-descent methods and
the global minimum of the classification error
for given training set is readily achieved by a
sequence of matrix operations of guaranteed
stability.
At very close distances to the lidar,
ss
RR
Δ
≤ 10 , the
shape factor of the smoke-plume signature does
depend on
sp
R
. However, it was observed that the
shape distortion does not affect the recognition
capability of the system for this region, mostly due
to very high PNR feature value that activates the
alarm output even if the input from the binary-
sample nodes is not univocal.
5 CONCLUSIONS AND FUTURE
WORK
The neural-network algorithm in question is
extremely flexible; it was successfully used for
automated signal processing in a variety of lidars,
including a system for forest fire surveillance
already deployed in Central Portugal within the
framework of the AGRO project supported by
Portuguese Ministry of Agriculture.
As compared to alternative methods of
automated fire detection, which mostly focus on
radiometry and video/infrared imaging (San-Miguel-
Ayanz et al., 2005), the present active technique, due
to its potentially higher sensitivity, offers quicker
response to the alarm situation. In addition,
automation of the 1D lidar signal processing is an
easier task than fire or smoke-plume recognition in
the 2D images provided by video/infrared cameras.
Future developments of the described algorithm
are connected with invoking additional information
extracted from statistical properties of the collected
lidar returns.
ACKNOWLEDGEMENTS
This research has been supported in part by Agência
de Inovação (AdI) within the framework of POCI
2010 program (FEDER funded), project SIDAI.
REFERENCES
Anderson, J.A., 1988. General Introduction. In.: Anderson,
J.A., Rosenfeld, E. (eds.): Neurocomputing:
Foundations of Research, MIT Press. Cambridge.
Bhattacharya, D., Pillai, S.R., Antoniou, A., 1997.
Waveform classification and information extraction
from lidar data by neural networks. IEEE Trans. on
Geoscience and Remote Sensing 35, 699-707.
Bishop, C.M., 1995. Neural Networks for Pattern
Recognition, Claredon Press. Oxford.
Fernandes, A.M., Utkin, A.B., Lavrov, A.V., Vilar, R.M.,
2004. Development of neural network committee
machines for automatic forest fire detection using
lidar. Pattern Recognition 37, 2039-2047.
Haykin, S., 1999. Neural Networks, Prentice Hall.
London, 2
nd
edition.
Kozlov, V.S., Panchenko, M.V., 1996. Investigation of
optical characteristics and particle-size distribution of
wood-smoke aerosols. Combustion, Explosion, and
Shock Waves 32, 577-586.
Mitra, V., Wang, C.J., Banerjee, S., 2003. Lidar detection
of underwater objects using neural networks with
linear prediction and fourier transform for feature
extraction. In Proceedings of Application of Neural
Networks in Engineering, ANNIE’2003, Vol. 13.
ASME Press. Missouri, 695-700.
Press, W.H., Flannerly, B.P., Teukolsky, S.A., Vetterling
W.T., 1986. Numerical Recipes: The Art of Scientific
Computing, Cambridge Univ. Press. Cambridge.
San-Miguel-Ayanz, J., Ravail, N., Kelha, V., Ollero, A.,
2005. Active fire detection for fire emergency
management: Potential and limitations for the
operational use of remote sensing. Natural Hazards
35, 361-376.
Utkin, A.B., Lavrov, A.V., Vilar, R.M., 2009. Low-cost
active optical system for fire surveillance. Optics and
Spectroscopy 106, 926-936.
IJCCI 2009 - International Joint Conference on Computational Intelligence
574
