A TUNABLE REAL-WORLD MULTI-FUNNEL BENCHMARK

PROBLEM FOR EVOLUTIONARY OPTIMIZATION

And Why Parallel Island Models Might Remedy the Failure of CMA-ES on It

Christian L. M¨uller and Ivo F. Sbalzarini

Institute of Theoretical Computer Science and Swiss Institute of Bioinformatics

ETH Zurich, Universit¨atstrasse 6, 8092 Zurich, Switzerland

Keywords:

Benchmark, Multi-funnel landscape, Lennard-Jones cluster, CMA-ES, Parallel island model.

Abstract:

A common shortcoming in the Evolutionary Computation (EC) community is that the publication of many

search heuristics is not accompanied by rigorous benchmarks on a balanced set of test problems. A welcome

effort to promote such testsuites are the IEEE CEC competitions on real-valued black-box optimization. These

competitions prescribe carefully designed synthetic test functions and benchmarking protocols. They do,

however, not contain tunable real-world examples of the important class of multi-funnel functions. We argue

that ﬁnding minimum-energy conﬁgurations of 38-atom Lennard-Jones (LJ

) clusters could serve as such

a benchmark for real-valued, single-objective evolutionary optimization. We thus suggest that this problem

be included in EC studies whenever general-purpose optimizers are proposed. The problem is tunable from

a single-funnel to a double-funnel topology. We show that the winner of the CEC 2005 competition, the

Evolution Strategy with Covariance Matrix Adaptation (CMA-ES), works on the single-funnel version of this

test case, but fails on the double-funnel version. We further argue that this performance loss of CMA-ES

can be relaxed by using parallel island models. We support this hypothesis by simulation results of a parallel

island CMA-ES, the Particle Swarm CMA-ES, on a subset of the multi-funnel functions in the CEC 2005

benchmark.

1 INTRODUCTION

High-dimensional, non-convex, and noisy optimiza-

tion problems are commonplace in physics, engineer-

ing, and biology. The prominent example of protein

structure prediction can, e.g., be considered a mini-

mization problem over an empirical energy landscape.

In many cases, such problemscan only be tackled efﬁ-

ciently by evolutionary optimization methods such as

the Evolution Strategy with Covariance Matrix Adap-

tation (CMA-ES) (Hansen and Ostermeier, 2001), a

particularly successful gradient-free heuristic for real-

valued black-box optimization. During exploration of

the search space, CMA-ES samples a population of

candidate solutions from a multivariate Gaussian dis-

tribution. The mean and the covariance matrix of the

sampling distribution are continuously adapted in or-

der to guide the search toward promising regions of

the space.

Assessing the efﬁcacy and efﬁciency of evolution-

ary algorithms is empirical by nature since theoreti-

cal convergence analyses are missing for most prob-

lems of practical importance. Unfortunately, it is

a common shortcoming in the Evolutionary Com-

putation (EC) community that many publications on

new search heuristics are not accompanied by rig-

orous benchmarks on a diverse and balanced set of

test problems. It is still commonplace that authors

choose an arbitrary set of popular benchmark func-

tions and compare the performance of their algorithm

to that of an arbitrary set of existing heuristics. A

welcome exception is the series of IEEE CEC compe-

titions on real-valued black-box optimization. Start-

ing in 2005 with a contest on single-objective black-

box optimization (Suganthan et al., 2005), these com-

petitions prescribe carefully designed synthetic func-

tion sets and benchmarking protocols. A generally

accepted standard set of real-world benchmark prob-

lems, however, is still not available.

While studies on synthetic test suites allowfair and re-

producible comparison between algorithms, they only

provide limited insight into why a particular heuris-

tic works on certain functions, but fails on others.

In recent years, it has been suggested that the global

248

L. Müeller C. and F. Sbalzar ini I. (2009).

A TUNABLE REAL-WORLD MULTI-FUNNEL BENCHMARK PROBLEM FOR EVOLUTIONARY OPTIMIZATION - And Why Parallel Island Models Might

Remedy the Failure of CMA-ES on It.

In Proceedings of the International Joint Conference on Computational Intelligence, pages 248-253

DOI: 10.5220/0002335202480253

 SciTePress

topology of a problem may have a strong inﬂuence

on the performance of search heuristics. (Hansen

and Kern, 2004) and (Sutton et al., 2006), for ex-

ample, suggested that the performance of CMA-ES

and Particle Swarm Optimization (PSO) can strongly

decrease on test functions with a multi-funnel topol-

ogy, where local optima cannot be interpreted as per-

turbations to an underlying convex (unimodal) topol-

ogy. (Lunacek et al., 2008) further examined this is-

sue by considering the search performance of CMA-

ES on synthetic, tunable double-funnel landscapes.

The global structure of these landscapes consists of

a composition of two sphere functions whose sizes

and depths are adjustable. They report two remark-

able observations. First, the probability of ﬁnding the

minimum with CMA-ES without restarts decreases

with increasing population size when considering a

double-sphere landscape where the global minimum

lies in the smaller funnel. Second, introduction of

local multi-modality in the double-sphere function

through a Rastrigin function triggers an irresolvable

trade-off for the optimal population size of CMA-

ES: Local multi-modality demands larger populations

while the double-funnel favors the opposite. There-

fore, the probability of ﬁnding the global minimum

with CMA-ES on the designed double-Rastrigin func-

tion is low for any population size. Unfortunately,

problemswith a multi-funnel structure are not of mere

academic interest. Prominent real-world examples

include trajectory planning in space missions, pro-

tein aggregation and misfolding (Clark, 2004), and

the potential-energy surfaces (PES) of atomic clusters

(Wales, 2004).

The purpose of the present paper is twofold. First, we

propose a tunable real-world benchmark problem for

real-valued, single-objective, gradient-free evolution-

ary optimization: the prediction of minimum-energy

conﬁgurations of the 38-atom Lennard-Jones (LJ

)

cluster. This problem has been intensively studied

in physical chemistry, and we expect this to be valu-

able to the EC community. The LJ

problem exhibits

a double-funnel PES topology (Doye et al., 1999),

which can be transformed to a single-funnel topology

by adding a compression penalty. This transforma-

tion is tunable by a single, scalar parameter. We show

that the LJ

cluster problem cannot be solved by the

winner of IEEE CEC 2005 contest, a restart variant of

CMA-ES with iteratively increasing population size

(IPOP-CMA-ES) (Auger and Hansen, 2005), unless

the compression penalty is included. We therefore

propose that the LJ

problem should be included in

future EC studies whenever a novel general-purpose

optimizer is introduced.

Second, we propose that the use of parallel island

models can remedy the decreased performance of

IPOP-CMA-ES on multi-funnel functions. We be-

lieve that it is beneﬁcial to evolve several commu-

nicating CMA-ES instances on the problem in par-

allel, rather than increasing the population size of a

single CMA-ES instance. We support this hypothesis

by simulation results of a parallel island CMA-ES, the

Particle Swarm CMA-ES (PS-CMA-ES), on a subset

of multi-funnel functions from the IEEE CEC 2005

test suite.

This paper is organized as follows: In Section 2 we

brieﬂy review the IEEE CEC 2005 benchmark test

suite and introduce the real-world multi-funnel en-

ergy landscape of the 38-atom Lennard-Jones clus-

ter. Section 3 reviews (IPOP-)CMA-ES, the concept

of parallel island models, and PS-CMA-ES. In Sec-

tion 4 we present the results of numerical experiments

with IPOP-CMA-ES and PS-CMA-ES. Section 5 dis-

cusses these results and concludes this work.

2 MULTI-FUNNEL

OPTIMIZATION PROBLEMS

Problems with a multi-funnel topology arise in di-

verse scientiﬁc areas such as, e.g., trajectory planning

in space missions or protein aggregation and misfold-

ing in biology. Although there is no clear mathemat-

ical deﬁnition of the term multi-funnel, we consider a

problem multi-funnel if it has no underlying convex

topology on a global length scale. Probably the best-

known example for a multi-funnel function is Schwe-

fel’s problem. The Rastrigin function, on the other

hand, is highly multi-modal, but not multi-funnel due

to its globally spherical topology. In this section, we

ﬁrst revisit the synthetic multi-funnel problems of the

IEEE CEC 2005 test suite and then propose the LJ

problem as a tunable real-world test case for gradient-

free optimization.

2.1 The IEEE CEC 2005 Test Suite

One key attempt to provide a standard for perfor-

mance evaluation and analysis of real-valued search

heuristics in the EC community is the IEEE CEC

2005 test suite (Suganthan et al., 2005). The bench-

mark suite includes a set of 25 test functions from a

variety of classes such as uni-/multimodal, (non-) sep-

arable, noisy, (a-)symmetric, and scalable. Functions

f11 to f13 and f15 to f25 are multi-funnel. Along with

the test functions, the suite also speciﬁes a detailed

protocol how to evaluate a search heuristic: the prob-

lem dimension ranges from n = 10. ..50, the number

of allowed function evaluations is restricted to n· 10

A TUNABLE REAL-WORLD MULTI-FUNNEL BENCHMARK PROBLEM FOR EVOLUTIONARY OPTIMIZATION

- And Why Parallel Island Models Might Remedy the Failure of CMA-ES on It

249

measures for success performance are deﬁned, and

examples of how to present the results in tables and

ﬁgures are provided. We refer to the original publi-

cation for the full description of the test suite (Sugan-

than et al., 2005). Here, we use functions f11 to f13,

f15, and f16 to evaluate the performance of IPOP- and

PS-CMA-ES on multi-funnel problems.

2.2 Lennard-Jones Clusters

The PES of Lennard-Jones (LJ) clusters is one of the

best studied models both in physical chemistry and,

to some extent, in the ﬁeld of global optimization.

The objective of ﬁnding the minimum-energy conﬁg-

uration of this model has fascinated researchers from

both communities for over three decades. Each pair

of atoms in a LJ cluster interacts through the LJ pair

potential

u(r

) = 4ε





−





, (1)

where r

is the distance between atoms X

and X

ε the potential-well depth (in units of energy) and

the equilibrium inter-atom distance (in units of

length) at zero temperature. The potential energy E

of a cluster of N LJ atoms is given by:

= 4ε

N−1

∑

i=1

∑

j=i+1





−





. (2)

In chemistry, the LJ potential is widely used to model

hydrophobic interactions in polymers or the behav-

ior of (noble) gases such as Argon. Knowledge about

minimum-energy (or ground-state) conﬁgurations of

LJ clusters enables, e.g., predicting properties of crys-

tallization or solid–liquid transitions at low temper-

atures. At the same time, LJ clusters are a model

problem for general-purpose non-convex optimiza-

tion. Minimizing the potential energy of a cluster of N

atoms in 3D space deﬁnes a continuous optimization

problem in 3N − 6 dimensions since 3 translational

and 3 rotational degrees of freedom can be removed

from the system. This is achieved by placing the ﬁrst

atom at the origin of the Cartesian coordinate system,

the second along the x-axis and the third in the x− −y

plane. Several general-purpose optimizers have been

tested on LJ clusters of various sizes, most notably the

Basin Hopping algorithm (Wales and Doye, 1997),

which makes extensive use of gradient information.

To date, ﬁnding the minimum-energyconﬁguration of

LJ clusters is only feasible for global search heuris-

tics that are allowed to exploit exact, analytical gra-

dients. All known putative minimum-energy conﬁgu-

rations are listed in the Cambridge Cluster Database,

providing a valuable resource for optimization bench-

marks. A particularly well-understood conﬁguration

is the 38-atom cluster, forming the basis for the new

benchmark problem proposed here.

2.2.1 The Energy Landscape of the 38-atom

Lennard-Jones Cluster

The topology of the LJ

PES has been extensively

studied in the literature (Doye et al., 1999; Doye,

2000; Wales, 2004). It exhibits a double-funnel struc-

ture where the global minimum-energy conﬁguration

with face-centered cubic octahedral (fcc) symmetry

lies in a narrow funnel and the majority of local min-

ima, all with icosahedral (ico) symmetry, populate the

wider funnel. Figure 1 shows a sketch of the land-

scape.

Potential Energy

Order Parameter

ico

fcc

Funnel 1

Funnel 2

Figure 1: Sketch of the PES of the 38-atom LJ cluster. The

x-axis represents a suitable order parameter that can dis-

criminate between different cluster topologies, the y-axis

represents the potential energy of the conﬁgurations. The

wide funnel on the left is populated by clusters with icosa-

hedral (ico) symmetry. The lowest-energy conﬁguration

with ico symmetry is depicted in blue. The narrow fun-

nel on the right contains the global minimum with face-

centered cubic octahedral (fcc) symmetry (depicted in red).

(Doye et al., 1999) characterized this landscape in

great detail in terms of the number and locations of

minima, structural diversity of the minima, and the

energy barrier between the two funnels. In a subse-

quent study, (Doye, 2000) also studied the effect of

compression on the PES of the 38-atom LJ cluster.

Compression can be seen as a transformation of the

PES that favors more compact structures. Hence, it

broadens the funnel of the more spherical fcc struc-

tures and narrows the ico funnel. Doye added the fol-

lowing compression penalty to the energy function:

CLJ

= E

+ µ

comp

∑

i=1

− X

, (3)

IJCCI 2009 - International Joint Conference on Computational Intelligence

250

where X

is the position of atom i and X

is the center

of mass of the cluster. The parameter µ

comp

controls

the magnitude of the compression acting on the con-

ﬁguration. When µ

comp

≥ 5ε, the PES of the cluster

exhibits a clear single-funnel topology. The effect of

the µ

comp

-dependent compression on the PES is beau-

tifully visualized in (Wales, 2004), pp. 338–339, and

(Doye, 2000). Note that even with the compressed

potential E

CLJ

the system contains a staggering num-

ber of local minima, but the global topology can be

changed from double-funnel to single-funnel. This

renders the 38-atom LJ cluster with tunable compres-

sion an ideal real-world test case to study the perfor-

mance of evolutionary algorithms and their sensitivity

to the underlying topology.

2.2.2 Bond-order Parameters for Cluster

Characterization

Bond-order parameters are indispensable for the anal-

ysis of cluster conﬁgurations (Steinhardt et al., 1983).

These parameters, termed Q

, Q

, W

, andW

are able

to discriminate symmetry groups in crystals and liq-

uids. The parameters Q

and Q

have been identi-

ﬁed as the most informative ones for distinguishing

fcc from ico conﬁgurations. Q

is deﬁned as:

4π

2l + 1

∑

m=−l

, (4)

where

∑

(Θ

,Φ

). (5)

Here, N

denotes the number of pseudo bonds that

have a length smaller than a cutoff distance r

(Θ

,Φ

) are spherical harmonics with Θ

being

the polar and Φ

the azimuthal angle of the inter-

atomic vector r

with respect to an arbitrary coordi-

nate frame. We propose to use the order parameter

with a cutoff of r

= 1.391σ

as suggested for

LJ cluster analysis (Doye et al., 1999). A Q

value

of 0 corresponds to a perfect icosahedron, a value of

0.1909 to a perfect fcc conﬁguration.

3 STANDARD CMA-ES AND

PARALLEL-ISLAND CMA-ES

This section reviews (IPOP-)CMA-ES and parallel is-

land models for CMA-ES.

3.1 The CMA Evolution Strategy

The standard CMA-ES uses weighted intermediate

recombination, step size adaptation, and a combina-

tion of rank-µ update and rank-one update (Hansen

and Ostermeier, 2001; Hansen, 2007). At each itera-

tion of the algorithm, the members of the new popula-

tion are sampled from a multivariate normal distribu-

tion N with mean m ∈ R

and covariance C ∈ R

n×n

The sampling radius is controlled by the overall stan-

dard deviation (step size) σ. Let x

(g)

the k

individ-

ual at generation g. The new individuals at generation

g+ 1 are sampled as:

(g+1)

∼ m

(g)

+ σ

(g)



0,C

(g)



k = 1,. ..,λ. (6)

The λ sampled points are then ranked in order of as-

cending ﬁtness, and the µ best are selected. The mean

of the sampling distribution is updated using weighted

intermediate recombination (Hansen, 2007). The

covariance matrix is adapted as described in vari-

ous publications and reports (Hansen and Ostermeier,

2001; Hansen, 2007). The behavior of CMA-ES is

mainly controlled by two parameters: the initial step

size σ and the population size λ. In standard CMA-

ES, the population size is chosen as λ = 4 + ⌊3lnn⌋

(Hansen and Ostermeier, 2001). The most success-

ful variant of CMA-ES, IPOP-CMA-ES, employs a

restart mechanism with iterative doubling of the pop-

ulation size until a stopping criterion is met (Auger

and Hansen, 2005). It uses an initial step size of

σ = (B − A)/2, where [A,B]

is the bounded search

space. These standard choices render IPOP-CMA-ES

quasi parameter-free.

3.2 Parallel Island Models for CMA-ES

The concept of parallel island models for evolution-

ary algorithms is to use a set of independent (possi-

bly heterogeneous) populations (islands) that concur-

rently explore the problem space. During search, the

populations are allowed to migrate (communicate in-

formation)in an (a-)synchronousway. Many different

migration patterns and modes of information sharing

have been examined in recent years. Two advantages

of parallel island models are that (a) different distant

parts of the search space can be explored simultane-

ously and integrated into individual populations, and

(b) such algorithms can easily be parallelized in a dis-

tributed computing environment. For detailed infor-

mation on the topic, we refer to (Alba, 2005).

A speciﬁc instance of a parallel island model for

CMA-ES, the Particle Swarm CMA-ES (M¨uller et al.,

2009), has been introduced in order to improve the

performance of CMA-ES on multi-funnel landscapes.

Inspired by ideas from Particle Swarm Optimization

(PSO), the PS-CMA-ES algorithm evolves a swarm

of S CMA-ES instances in parallel. The individual

A TUNABLE REAL-WORLD MULTI-FUNNEL BENCHMARK PROBLEM FOR EVOLUTIONARY OPTIMIZATION

- And Why Parallel Island Models Might Remedy the Failure of CMA-ES on It

251

instances exchange promising solutions every I

gen-

erations. Both the swarm size S (the total number of

concurrent CMA-ES instances) and the communica-

tion interval I

are strategy parameters. The inﬂuence

of global swarm information on the covariance matrix

adaptation of each CMA-ES instance is controlled by

a weight parameter c

∈ [0,1]. A detailed description

of the algorithm can be found in (M¨uller et al., 2009).

4 COMPUTATIONAL

EXPERIMENTS

We ﬁrst show the performance of IPOP-CMA-ES on

and then assess IPOP- and PS-CMA-ES on a

multi-funnel subset of the CEC 2005 test suite.

4.1 The 38-Atom LJ Cluster

We search for the minimum-energy conﬁgurations of

in a 3D [−4,4] box. The search space thus is

[−4,4]

with dimension n = 3· 38− 6 = 108. The LJ

parameters σ

and ε are both set to 1. In order to as-

sess the effectiveness of IPOP-CMA-ES on LJ

, we

follow the parameterization and boundary handling of

(Auger and Hansen, 2005) with two important excep-

tions. Instead of doubling the population size after

each restart, we increase λ by a factor of 1.25. We

also reﬁne the initialization procedure in order to as-

sess the effect of initial LJ-particle positions on the

quality of the solution: We place the initial popula-

tion mean uniformly random in the box [−0.5,0.5]

[−1.5,1.5]

, or [−3,3]

and sample the initial popu-

lation with a σ of 20% of the box edge length. We

repeat the experiment 25 times for each box size with

no bounds on the number of allowed function evalua-

tions. We stop an optimization run whenever the pop-

ulation size exceeds the initial λ by a factor of 100,

i.e., after 21 restarts. We consider LJ

clusters with-

out compression and with µ

comp

= 5ε.

Figure 2 summarizes the results. The experiments re-

veal that on the LJ

problem without compression

none of the IPOP-CMA-ES runs reach the lowest-

energy fcc conﬁguration, nor the lowest-energy ico

conﬁguration (blue  in Figure 2), despite the fact

that each run used, on average, 10

function evalua-

tions. With compression, however, all IPOP-CMA-

ES runs ﬁnd the globally optimal fcc conﬁgura-

tion, independent of initialization. Even more strik-

ingly, all local minima found on the problem with-

out compression have icosahedral-like conﬁgurations

with Q

values between 0.01 and 0.045. The runs

that started in the largest box (blue •’s in Fig. 2)

show the largest structural diversity of the minima

!" !# !$ ! !% &' &( &!

%)%$

%)%"

%)%&

%)%(

%) $

%) "

%) &

%) (

%)$

Energy

[

]

Structural transition regio

Figure 2: Bond-order parameter Q

vs. potential energy

(in units of ε) for all minima found by IPOP-CMA-ES.

The blue data points show the 3 · 25 local minima found

on the LJ

problem without compression with the ini-

tial [−0.5,0.5]

box (×), the [−1.5,1.5]

box (◦), and the

[−3,3]

box (•). The single blue  in the bottom-left cor-

ner marks the lowest-energy icosahedral conﬁguration. The

shaded gray area is the structural transition region from ico

to fcc symmetry (Doye et al., 1999). The red data point

in the upper-left corner corresponds to the global minimum

= −173.9284ε), which was found by IPOP-CMA-ES

in all 3· 25 runs when using the compression penalty.

= 0.01. ..0.045), including the lowest local min-

imum found at E

≈ −170.66ε. All runs that started

in the [−1.5,1.5]

box converged to the same local

minimum, while the runs in the smallest box found

an additional local minimum.

4.2 The IEEE CEC 2005 Test Suite

We provide evidence that the failure of IPOP-CMA-

ES on multi-funnel functions can be remedied by us-

ing a parallel island model instead of a single popu-

lation of increasing size. Therefore, we compare the

performanceof the parallel island PS-CMA-ES to that

of IPOP-CMA-ES on the multi-funnel functions f11

to f13, f15, and f16 of the CEC 2005 benchmarksuite.

The results are summarized in Table 1. All experi-

ments are conducted according to the CEC 2005 pro-

tocol. While IPOP-CMA-ES is still quite efﬁcient on

the modiﬁed Weierstrass function (f11) and Schwe-

fel’s problem (f12), it is not able to solve any of the

other multi-funnel functions in the set. PS-CMA-ES

can solve f11 to f13 with strategy parameters c

= 0.7,

= 200, and S = 15, and f15 and f16 with strat-

egy parameters c

= 0.3, I

= 150, and S = 10. To

our knowledge, no other algorithm has so far been re-

ported to solve the pair f15/f16.

IJCCI 2009 - International Joint Conference on Computational Intelligence

252

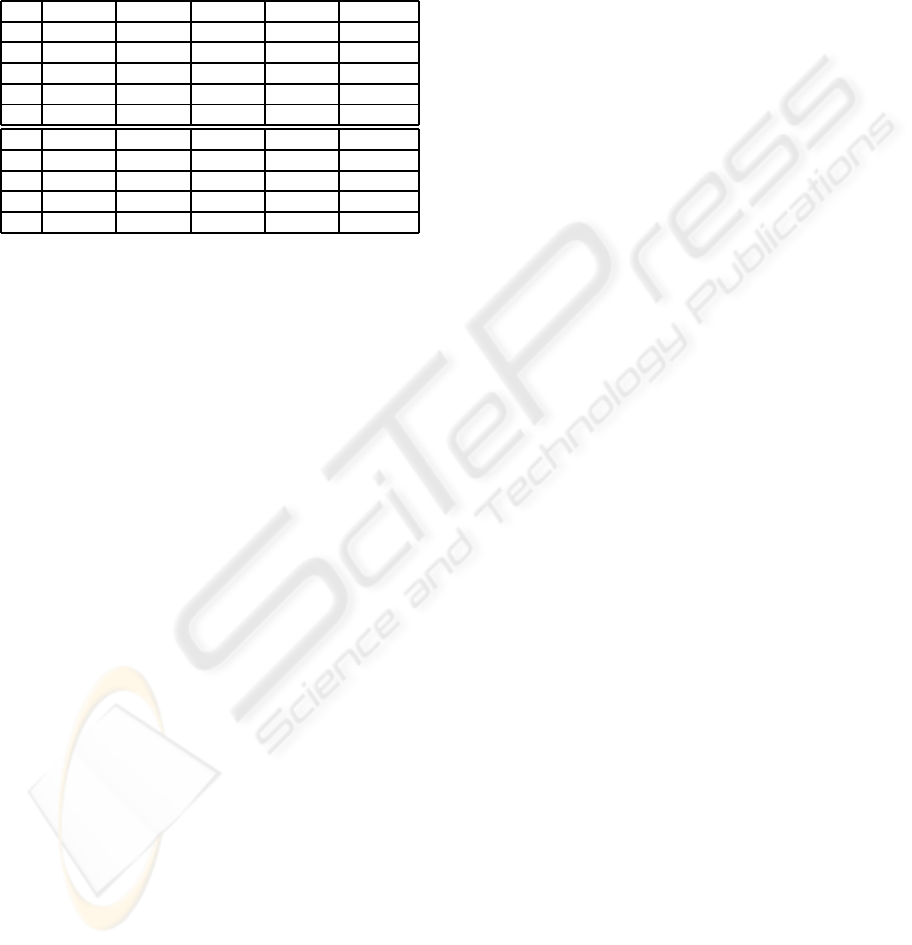
Table 1: Summary statistics of IPOP-CMA-ES (ﬁrst block,

taken from (Auger and Hansen, 2005)) and PS-CMA-ES

(second block) on the multi-funnel functions f11 to f13,

f15, and f16 of the CEC 2005 test suite in n = 10 dimen-

sions. The minimum, median, maximum, and mean num-

ber of function evaluations needed to solve the problems

are reported over 25 repetitions of each test. The last col-

umn reports the success rates. See main text for strategy

parameters used.

min med max mean Suc. Rate

f11 3.05e+04 - - 6.31e+4 2.40e-01

f12 2.37e+03 3.10e+04 - 2.88e+04 8.80e-01

f13 - - - - 0

f15 - - - - 0

f16 - - - - 0

f11 3.56e+04 - - 5.02e+04 4.00e-01

f12 1.66e+04 1.89e+04 2.13e+04 1.92e+04 1.00e+00

f13 8.34e+04 - - 8.34e+04 4.00e-02

f15 3.30e+04 - - 3.65e+04 1.20e-01

f16 5.09e+04 - - 5.09e+04 4.00e-02

5 CONCLUSIONS

In summary, we have proposed: (a) a tunable real-

world multi-funnel test case for gradient-free evolu-

tionary optimizers and (b) that parallel island models

can relax the performance decrease of CMA-ES on

multi-funnel functions where the global optimum is

not located in the broadest funnel. The latter can be

explained by the irresolvable trade-off for the optimal

population size of CMA-ES on multi-funnelfunctions

(Lunacek et al., 2008). The larger the population size,

the more likely CMA-ES converges in the broadest,

sub-optimal funnel. This is supported by the fact that

IPOP-CMA-ES performs remarkably well when the

PES of LJ

is compressed to a single-funnel structure

and that the parallel island PS-CMA-ES outperforms

IPOP-CMA-ES on the considered sub-set of multi-

funnel functions from the CEC 2005 test suite. To

date, no population-based, gradient-free evolutionary

algorithm can solve the presented LJ

test case with-

out compression. Since many real-world applications

entail multi-funnel landscapes, we argue that the EC

community should focus on algorithms that can solve

such problems. As a benchmark, we suggest the LJ

problem, which should be considered in all future EC

studies that introduce a novel general-purpose opti-

mizer.

ACKNOWLEDGEMENTS

We thank Georg Ofenbeck for setting up the LJ cluster

simulations.

REFERENCES

Alba, E. (2005). Parallel Metaheuristics: A New Class of

Algorithms. Wiley-Interscience.

Auger, A. and Hansen, N. (2005). A restart CMA evolu-

tion strategy with increasing population size. In Proc.

IEEE Congress on Evolutionary Computation (CEC

2005), volume 2, pages 1769–1776.

Clark, P. L. (2004). Protein folding in the cell: reshaping

the folding funnel. Trends Biochem. Sci., 29(10):527–

534.

Doye, J. (2000). Effect of compression on the global opti-

mization of atomic clusters. Phys. Rev. E, 62(6, Part

B):8753–8761.

Doye, J. P. K., Miller, M. A., and Wales, D. J. (1999).

The double-funnel energy landscape of the 38-atom

Lennard-Jones cluster. J. Chem. Phys., 110(14):6896–

6906.

Hansen, N. (2007). The CMA Evolution Strategy: A Tuto-

rial. http://www.lri.fr/ hansen/cmatutorial.pdf.

Hansen, N. and Kern, S. (2004). Evaluating the CMA Evo-

lution Strategy on Multimodal Test Functions. In Lect.

Notes Comput. Sc., volume 3242 of Parallel Problem

Solving from Nature - PPSN VIII, pages 282–291.

Hansen, N. and Ostermeier, A. (2001). Completely Deran-

domized Self-Adaption in Evolution Strategies. Evo-

lutionary Computation, 9(2):159–195.

Lunacek, M., Whitley, D., and Sutton, A. (2008). The Im-

pact of Global Structure on Search. In Lect. Notes

Comput. Sc., volume 5199 of Parallel Problem Solv-

ing from Nature - PPSN X, pages 498–507.

M¨uller, C. L., Baumgartner, B., and Sbalzarini, I. F. (2009).

Particle swarm CMA evolution strategy for the opti-

mization of multi-funnel landscapes. In Proc. IEEE

Congress on Evolutionary Computation (CEC 2009),

pages 2685–2692.

Steinhardt, P. J., Nelson, D. R., and Ronchetti, M. (1983).

Bond-orientational order in liquids and glasses. Phys.

Rev. B, 28(2):784–805.

Suganthan, P. N., Hansen, N., Liang, J. J., Deb, K., Chen,

Y.-P., Auger, A., and Tiwari, S. (2005). Problem Deﬁ-

nitions and Evaluation Criteria for the CEC 2005 Spe-

cial Session on Real-Parameter Optimization. Techni-

cal report, Nanyang Technological University, Singa-

pore.

Sutton, A. M., Whitley, D., Lunacek, M., and Howe, A.

(2006). PSO and multi-funnel landscapes: how co-

operation might limit exploration. In Proc. ACM

Genetic and Evolutionary Computation Conference

(GECCO’06), pages 75–82. ACM.

Wales, D. (2004). Energy Landscapes : Applications

to Clusters, Biomolecules and Glasses (Cambridge

Molecular Science). Cambridge University Press.

Wales, D. J. and Doye, J. P. K. (1997). Global Optimiza-

tion by Basin-Hopping and the Lowest Energy Struc-

tures of Lennard-Jones Clusters Containing up to 110

Atoms. J. Phys. Chem. A, 101(28):5111–5116.

A TUNABLE REAL-WORLD MULTI-FUNNEL BENCHMARK PROBLEM FOR EVOLUTIONARY OPTIMIZATION

- And Why Parallel Island Models Might Remedy the Failure of CMA-ES on It

253