FEATURE AND COMPUTATIONAL TIME REDUCTION ON

HAND BIOMETRIC SYSTEM

Carlos M. Travieso

, Jordi Solé-Casals

, Miguel A. Ferrer

and Jesús B. Alonso

Signals and Communication Department, Technological Centre for Innovation in Communnications

University of Las Palmas de Gran Canaria, Campus de Tafira, sn, Ed. de Telecomuncación

Pabellón B, Despacho 111, E35017, Las Palmas de Gran Canaria, Spain

Digital and Information Technologies Department, Digital Technologies Group, University of Vic

c/ de la Laura, 13, E-08500, Vic, Barcelona, Spain

Keywords: Principal Component Analysis, Pattern Recognition, Hand Biometric System, Parameterization, Feature

reduction, Classification system.

Abstract: In real-time biometric systems, computational time is a critical and important parameter. In order to improve

it, simpler systems are necessary but without loosing classification rates. In this present work, we explore

how to improve the characteristics of a hand biometric system by reducing the computational time. For this

task, neural network-multi layer Perceptron (NN-MLP) are used instead of original Hidden Markov Model

(HMM) system and classical Principal Component Analysis (PCA) procedure is combined with MLP in

order to obtain better results. As showed in the experiments, the new proposed PCA+MLP system achieves

same success rate while computational time is reduced from 247 seconds (HMM case) to 7.3 seconds.

1 INTRODUCTION

Biometrics is an emerging technology which is used

to identify or verify people by their physical or

behavioral characteristics. Amongst the physical

characteristics which have been used in biometrics

are the fingerprint, hand geometry, palm-print, face,

iris, retina, ear, etc. (Jain et al., 2001).

While systems based on fingerprint and eyes

features have, at least to date, achieved the best

matching performance, human hand provides the

source for a number of physiological biometric

features. The most frequently used are fingerprint,

palm-print, hand geometry, fingers geometry and

hand edge. These human hand features are relatively

stable and all the above mentioned characteristics

can be easily extracted from one single image of the

hand. Furthermore, these identification systems are

very well accepted by users, as are simples and do

not require to do anything special.

In this paper hand edge and its feature and time

computational reduction have been studied as a first

step for a real time application. We have worked on

a new parameterization for the hand edge, and after

the study of its behaviour, we have applied PCA

method in order to reduce the feature vector and

computational load of the system.

2 DATABASE

Our database has been built based on 60 users,

acquiring 10 samples per user. A scanner has been

used in order to acquire each sample. The following

table shows the most important characteristics of our

database.

Table 1: Characteristics of our database.

Parameters Data Example

Number of

classes

Number of

samples per

classes

Acquisition and

Quantification

Gray Scale (8

bits, 256 levels)

Resolution 150 dpi

Size

1403 x 1021

pixels

reduced to 80%

367

Travieso C., Solé-Casals J., Ferrer M. and Alonso J. (2010).

FEATURE AND COMPUTATIONAL TIME REDUCTION ON HAND BIOMETRIC SYSTEM.

In Proceedings of the Third International Conference on Bio-inspired Systems and Signal Processing, pages 367-372

DOI: 10.5220/0002591503670372

 SciTePress

3 PARAMETERIZATION

SYSTEM

We have considered just the hand perimeter. This

image is considered without the wrist that has been

extracted automatically from the shadow image.

Hands are scanned placed more or less on the center,

upward (wrist down).

Border determination as (x,y) positioning

perimeter pixels of black intensity, has been

achieved by processes of shadowing (black shape

over white background), filtering of isolated points,

and perimeter point to point continuous follow.

3.1 Perimeter Interpolation

Perimeter size variability induces us to consider a

convenient perimeter point interpolation, in order to

standardize perimeter vector description. For an

interpolating process, in order to achieve

reconstruction of the original shape, we may use any

of the well known algorithms as mentioned in (Fu

and Milios, 1994), (Loncaric, 1998), (Huang and

Cohen, 1996), but a simple control point’s choice

criterion in 1-D analysis allows for an appropriate

performance ratio on uniform control point’s

number and approximation error for all individuals

of all varieties studied.

The general idea, for such choice, is to consider

(x,y) positional perimeter points as (x,F(x)) graph

points of a 1-D relation F.

Consideration of y coordinate as y = F(x) is

done, because of the way, hands images are

presented in our study: hands have been scanned

with maximum size placed over x ordinate.

For a relation G to be considered as a one-

dimensional function, there is need to preserver a

correct sequencing definition (monotonic behavior).

That is: A graph,

)}(/),(,..1{

xniG ===

(1)

It is the description of a function f if ordinate

points

nix

..1, = must be such that:

1..1,

−=<

nixx

We consider then the border relation F as a union

of piece like curves (graphs) preserving the

monotonic behavior criterion, i.e.

∪

∈

(2)

where:

JjFG

∈∀⊆ , and

}/),(,{

jjjj

fyyxJG

jjj

∈

ααα

For convenient sets of index J, J

and restriction

functions

}|{|

Jxj

∈

, such that the next point

following the last of G

is the first one of G

+1. G

graphs are correct f

functions descriptions.

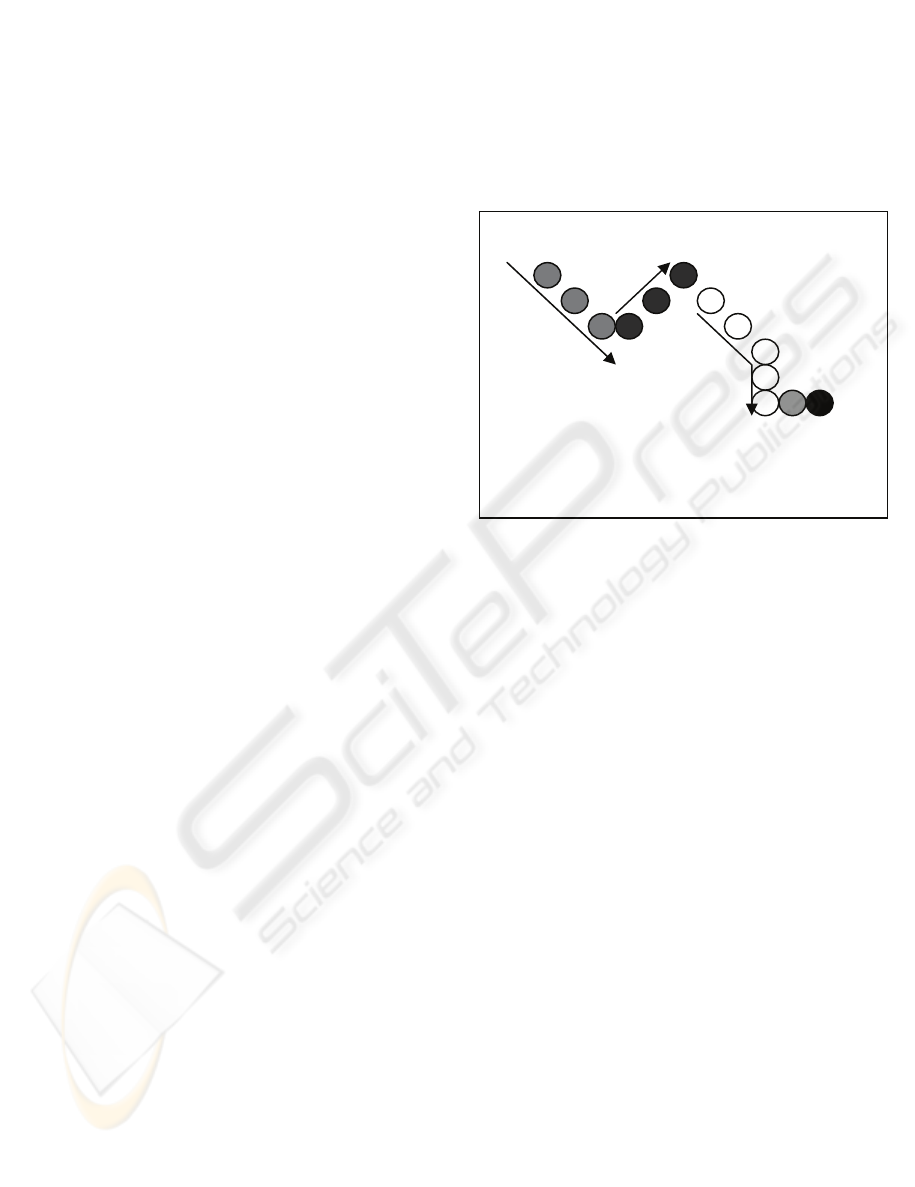
Figure 1: Example of an F relation decomposed in graphs

with a correct function description.

Building the G

sets is a very straightforward

operation:

 Beginning with a first point we include the next

one of F.

 As soon as this point doesn’t preserve

monotonic behaviour we begin with a new Gj

+1.

 Processes stop when all F points are assigned.

In order to avoid building G

reduced to

singletons, as show in figure 1 (G

and G

) the

original F relation may be simplified to preserve

only the first point of constant x ordinate series.

Afterwards, spreading of a constant number of

points is done proportional to the length of the G

and always setting in it is first one.

The point’s choice criterion mentioned before

allows, in two-dimensional interpolation, for taking

account on points where reverse direction changes

take place. Irregularity, of the surface curve, is

taken into account with a sufficient number of

interpolating points, as done in the uniform

spreading way.

The 1-D interpolation has been perform using

between 750 and 100 control points, with spline,

lineal or closest interpolated point neighborhood,

depending on the number of control points present

F = G

1∪

2∪

3∪

4∪

BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing

368

in the decomposed curve. As a reference at 300 dpi a

crayon free hand trace is about 5 to 6 points wide.

Due to perimeter size variability inside a class,

coding of (x,y) control perimeter points have been

transformed taking account for size independence.

Considering the following definitions:

Γ the set of n, a fixed number, of control

points,

)},(/{

..1 iiini

yxXX ==Γ

Where (x

) are

point coordinates of control perimeter points.

the central point of the

set:

),)(/1(

..1..1

∑∑

nini

yxnC

Γ∈

= niii

..1

),(

)(),(

1010 ++

iiiiii

XCXangleXXCangle

angles

defined for each interpolating points of

Γ .

Sequences of (x

) positional points are then

transformed in sequence of

()

, angular points.

The choice of a starting and a central point

accounts for scale and leaf orientation. Placement of

both points sets the scale: its distance separation.

Relative point positioning sets the orientation of the

interpolating shape. Given a sequence of such angles

and

, it’s then possible to reconstruct the

interpolating shape of a leaf. Geometrical properties

of triangle similarities make such sequence size and

orientation free.

4 REDUCTION PARAMETERS

Principal Components Analysis (PCA) is a way of

identifying patterns in data, and expressing the data

in such a way as to highlight their similarities and

differences (Jolliffe, 2002). Since patterns in data

can be hard to find in data of high dimension, where

the luxury of graphical representation is not

available, PCA is a powerful tool for analyzing data.

The other main advantage of PCA is that once you

have found these patterns in the data, and you

compress the data, i.e. by reducing the number of

dimensions, without much loss of information.

PCA is an orthogonal linear transformation that

transforms the data to a new coordinate system such

that the greatest variance by any projection of the

data comes to lie on the first coordinate (called the

first principal component), the second greatest

variance on the second coordinate, and so on. PCA

is theoretically the optimum transform for a given

data in least square terms.

In PCA, the basis vectors are obtained by solving

the algebraic eigenvalue problem

(

)

RXXR

Λ where X is a data matrix whose

columns are centered samples, R is a matrix of

eigenvectors, and

is the corresponding

diagonal matrix of eigenvalues. The projection of

data

XRC

= , from the original p dimensional

space to a subspace spanned by n principal

eigenvectors is optimal in the mean squared error

sense.

Another possibility, not presented here, is to use

Independent Component Analysis (ICA) (Jutten and

Herault, 1991), (Hyvärinen et al. 2001) instead of

PCA. In this case, we obtain independent

coordinates and not only orthogonal as in previous

case. ICA has been used for dimensional reduction

and classification improvement with success

(Sanchez-Poblador et al., 2004).

In our problem we have 60 different classes of

hands, and for each class we have 10 different

samples, where each one is a two column matrix

between 750 and 100 points. First column

corresponds to interior angles

and second

column to exterior angles

, as explained before.

The procedure for applying PCA can be

summarized as follows:

1. Subtract the mean from each of the data

dimensions. This produces a data set whose

mean is zero (X).

2. Calculate de covariance matrix (Covx)

3. Calculate the eigenvectors e

and eigenvalues λ

of Covx

4. Order the eigenvectors e

by eigenvalue λ

highest to lowest. This gives us the components

in order of significance.

5. Form a feature vector by taking the eigenvectors

that we want to keep from the list of

eigenvectors, and forming a matrix (R) with

these eigenvectors in the columns.

6. Project the data to a subspace spanned by these

n principal components.

5 CLASSIFICATION SYSTEM

As classification system, two different models have

been used in this present work. Hidden Markov

Models (HMM), and Neural Networks (NN).

5.1 Hidden Markov Models

An HMM is the representation of a system in which,

for each value that takes a variable t, called time, it

FEATURE AND COMPUTATIONAL TIME REDUCTION ON HAND BIOMETRIC SYSTEM

369

is found in one and only one of N possible states and

declares a certain value at the output. Furthermore,

an HMM has two associated stochastic processes:

one hidden associate with the probability of

transition between states (non observable directly);

and another observable one, an associate with the

probability of obtaining each of the possible values

at the output, and this depends on the state in which

the system has been found (Rabiner and Juang,

1993). It has been used a Discrete HMM (DHMM),

which is defined by (Rabiner and Juang, 1993) and

(Rabiner, 1989);N is the number of states,

• M is the number of different observations,

• A(N,N) is the transition probabilities matrix

from one state to another,

• π(N,1) is the vector of probabilities that the

system begins in one state or another;

• and B(N,M) is the probabilities matrix for

each of the possible states of each of the

possible observations being produced.

We have worked with an HMM called "left to right"

or Bakis, which is particularly appropriate for

sequences. These “left to right” HMM’s turn out to

be especially appropriate for signature edge because

the transition through the states is produced in a

single direction, and therefore, it always advances

during the transition of its states. This provides for

this type of model the ability to keep a certain order

with respect to the observations produced where the

temporary distance among the most representative

changes. Finally, it has been worked from 40 to 80

states and 32 symbols per state.

In the DHMM approach, the conventional

technique for quantifying features is applied. For

each input vector, the quantifier takes the decision

about which is the most convenient value from the

information of the previous input vector. To avoid

taking a software decision, a fixed decision on the

value quantified is made. In order to expand the

possible values that the quantifier is going to

acquire, multi-labelling is used, so that the possible

quantified values are controlled by varying this

parameter. The number of labels in the DHMM is

related to values that can be taken from the number

of symbols per state.

DHMM algorithms should be generalized to be

adjusted to the output multi-labelling ({v

}k=1,..C),

to generate the output vector ({w(x

)}k=1,..,C).

Therefore, for a given state j of DHMM, the

probability that a vector x

is observed in the instant

t, can be written as;

∑

jkttj

kbvxwxb

)(),()(

(3)

where b

(k) is the output discrete probability,

associated with the value v

and the state j; being C

the size of the vector values codebook.

5.2 Neural Networks

In recent years several classification systems have

been implemented using classifying techniques, such

as Neural Networks. The widely used Neural

Networks techniques are much known on

applications of pattern recognition.

The Perceptron of a simple layer establishes its

correspondence with a rule of discrimination

between classes, based on the lineal discriminator.

However, it is possible to define discriminations for

not lineally separable classes using multilayer

Perceptrons that are networks without refreshing

(feed-forward) with one or more layers of nodes

between the input layer and exit layer. These

additional layers contain hidden neurons or nodes,

are directly connected to the input and output layer

(Bishop, 1995).

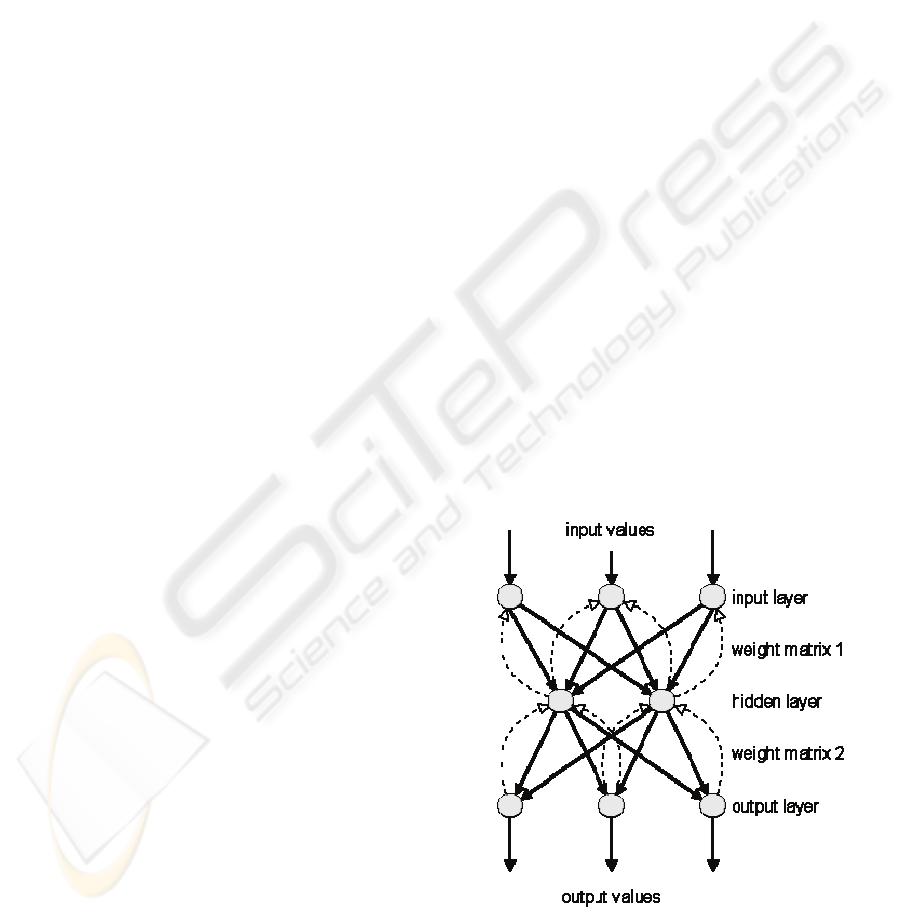
A neural network multilayer perceptron (NN-

MLP) of three layers is shown on figure 2 and

implemented, with two layers of hidden neurons.

Each neuron is associated with weights and biases.

These weights and biases are set to each connections

of the network and, are obtained from training in

order to make their values suitable for the

classification task between the different classes. We

have used a back-propagation algorithm in order to

train the classification system.

Figure 2: Multilayer Perceptron.

BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing

370

6 EXPERIMENTS AND RESULTS

All experiments have been repeated 5 fives or more,

therefore, the successes are showed by mean and

standard deviation. The first experiment was to find

the number of points more discriminate for the hand

edge. From 750 to 100 edge points were used, and

the best success was achieved with 200 points (see

table 2).

After this experiment, we begin to study the

feature reduction in order to keep the same success

rate. PCA method was used for this task.

Different number of components is considered in

the experiment, from 5 to 59 (as we have 60

different classes). As expected, the best

classification result was achieved with the maximum

number of principal components. Table 3

summarizes the success rates (only one experiment

for each case) obtained with different number of

principal components and using a multilayer

perceptron (MLP) as a classification system. The

neural network consisted of as many inputs as

principal components in the first layer, a hidden

layer of 60 nonlinear neurons (with tanh(·) as

activation function) and an output layer of 60

neurons. Scaled conjugate gradient was selected as

optimization algorithm, with a maximum of 500

epochs. Half of the examples where used for training

and the rest for test.

Table 2: Success rates for HMM classifier, using edge

information.

Table 3: Success rates for MLP classifier, using edge

information.

Number of

Principal Components

Success rates

46.00%

68.33%

75.00%

79.33%

78.33%

76.33%

78.00%

78.33%

78.67%

79.33%

83.33%

In order to explore the performances of the

system, we repeat 20 times the classification

algorithm with MLP, for 20, 40 and 59 principal

components (see Table 4). Mean computational time

of the algorithm was also calculated, and for the

sake of comparison, we trained also a MLP with all

the available parameters without any PCA reduction

(corresponding to last line in Table 4).

Table 4: Success rates for MLP classifier, using edge

information.

Number of

Principal

Components

Success rates

Mean time

(seconds)

78.75% ± 0.81 7.30

80.93% ± 0.92 7.31

83.77% ± 1.34 7.30

398 features

83.60% ± 0.92 67.43

We can see that 59 components give us a success

rate as well as the HMM model while reducing the

standard deviation. On the other hand, if no PCA

algorithm is used, the system works well but the

computational time need for the system is higher (by

a factor of 10). For the HMM case, computational

time is much higher, about 247 seconds, and it can

be a problem in some real-time applications.

Taking all the results in consideration, in table 4

is shown that MLP can obtain similar results as

HMM (see table 2), and by using PCA, it has

dramatically been reduced the computational time,

as we deal with a much simpler classification

system. This point is crucial in real-time operating

systems and justifies the use of PCA+MLP

architecture instead of HMM solution.

Number of

edge points

HMM

states

Number of

samples

training

Success rates

750 60

4 46.61% ± 5.94

3 38.09% ± 4.73

2 32.41% ± 4.67

1 23.55% ± 3.73

300 60

4 72.50% ± 4.77

3 71.90% ± 4.36

2 61.04% ± 6.48

1 54.37% ± 5.71

200 60

4 84.17% ± 6.40

3 82.33% ± 4.33

2 79.79% ± 4.03

1 73.92% ± 5.64

100 60

4 73.12% ± 6.21

3 71.00% ± 7.84

2 70.33% ± 2.33

1 65.63% ± 5.63

FEATURE AND COMPUTATIONAL TIME REDUCTION ON HAND BIOMETRIC SYSTEM

371

7 CONCLUSIONS

In this work we have presented a PCA+MLP

architecture in order to classify 60 different classes

of hands that keeps the success rate achieved by a

HMM classification system, but with an important

improvement on the computational time reduction.

From HMM to MLP the computational time was

reduced by a factor of 33, and by using PCA we

have achieved to reduce 10 times more the

computational time. This is the first step to get this

application on real time, taking in account that the

implementation has been done in MATLAB

language.

Future work will include the study of

Independent Component analysis (ICA) as a feature

reduction dimension system in order to improve

success rates. Too, a verification system and a fusion

with geometry features will be implemented.

ACKNOWLEDGEMENTS

This work has been in part supported by “Programa

José Castillejo 2008” from Spanish Government

under the grant JC2008-00398; by the University of

Vic under de grant R0904; by private funds from

Spanish Company Telefónica, under “Cátedra

Teléfonica-ULPGC 2009”; and by funds from

Research Action from Excellent Networks on

Biomedicine and Environment belonging to

ULPGC.

REFERENCES

Jain., A., Bolle, R., Pankati, S., 2001. BIOMETRICS:

Personal Identification in Networked Society, Kluwer

Academic Press, 3

edition.

Lu, F. Milios, E.E., 1994. Optimal Spline Fitting to Planar

Shape, Elsevier Signal Processing No. 37- pp 129-140

S. Loncaric, S., 1998, A Survey of Shape Analysis

Techniques, Pattern Recognition. Vol 31 No. 8, pp.

983-1001

Huang, Z., Cohen, F., 1996, Affine-Invariant B-Spline

Moments for Curve Matching, IEEE Transactions on

Image Processing, Vol. 5. No. 10 , pp 824-836

Jolliffe I.T., 2002, Principal Component Analysis, Series:

Springer Series in Statistics, 2nd ed., Springer, NY

Jutten, C., Herault, J., 1991, Blind separation of sources,

Part 1: an adaptive algorithm based on neuromimetic

architecture, Signal Processing (Elsevier), Vol. 24 ,

Issue 1.

Hyvärinen, A., Karhunen, J., Oja, E., 2001, Independent

Component Analysis, New York, USA: John Wiley &

Sons

Sanchez-Poblador, V., Monte Moreno, E., Solé-Casals, J.,

2004. ICA as a preprocessing technique for

Classification”, ICA 2004, Granada, Spain. Lecture

Notes in Computer Science, Springer-Verlag Volume

3195/2004.

Rabiner, L., Juang, B.H., 1993. Fundamentals of Speech

Recognition. Ed. Prentice Hall

Rabiner, L.R., 1989. A tutorial on Hidden Markov models

and Selected Applications in Speech Recognition.

Proceedings of the IEEE. 77 (2), pp. 275-286

Bishop, C.M., 1995. Neural Networks for Pattern

Recognition. Ed. Oxford University Press.

BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing

372