
DYNAMIC IMAGE SEGMENTATION SYSTEM
WITH MULTI-SCALING SYSTEM FOR GRAY SCALE IMAGE
Ken’ichi Fujimoto
†
, Mio Musashi
‡
and Tetsuya Yoshinaga
†
†Institute of Health Biosciences, The University of Tokushima
‡Graduate School of Health Sciences, The University of Tokushima
3-18-15 Kuramoto, Tokushima 770-8509, Japan
Keywords:
Dynamic image segmentation, Coupled system, Chaotic neurons, Gray scale image, Multi-scaling of gray
levels.
Abstract:
In this paper, we describe an image segmentation technique for a gray scale image by utilizing the nonlinear
dynamics of two respective discrete-time dynamical systems. The authors have proposed a discrete-time dy-
namical system that consists of a global inhibitor and chaotic neurons that can generate oscillatory responses.
By utilizing oscillatory responses, our system can perform dynamic image segmentation, which denotes seg-
menting image regions in an image and concurrently exhibiting segmented images in time series, for a binary
image. In order that our system can work for a gray scale image, we introduce a multi-scaling system as a
pre-processing unit of our system. It is also made of a discrete-time dynamical system and can find an image
region composed of pixels with different gray levels by multi-scaling gray levels of pixels. In addition, it can
compute the proximity between pixels based on their multi-scaled gray levels. Computed proximity becomes
significant information for designing parameters in our system. We demonstrated that our dynamic image
segmentation system with the multi-scaling system works well for a gray scale image.
1 INTRODUCTION
Image segmentation is the first essential and impor-
tant step in a low-level vision system and a computer-
aided diagnosis support system. A lot of frameworks
that provide static image segmentation have been de-
veloped (Pal and PAL, 1993).
In contrast to static image segmentation tech-
niques, a locally excitatory globally inhibitory oscil-
lator network (LEGION) (Wang and Terman, 1995)
can perform image segmentation dynamically, which
denotes segmenting isolated image regions in a static
image and concurrently exhibiting the segmented im-
ages in time series. A LEGION has a global inhibitor
and the same number of oscillators as pixels in an in-
put image, and its dynamics is described by ordinary
differential equations. Dynamic image segmentation
is based on oscillatory responses of oscillators, which
is a nonlinear phenomenon observed in a LEGION.
Dynamic image segmentation using a LEGION
needs a high computational cost in a digital com-
puter, since it is a continuous-time dynamical system.
As a more suitable dynamic image segmentation sys-
tem for digital computing, the authors have developed
a discrete-time dynamical system (Fujimoto et al.,
2008) with a global inhibitor and chaotic neurons (Ai-
hara et al., 1990) that can generate an oscillatory re-
sponse. The architecture of our system is similar to a
LEGION, and our system can perform dynamic im-
age segmentation based on oscillatory responses of
chaotic neurons. We analyzed suitable parameter val-
ues and demonstrated that our system works well for
a binary image (Fujimoto et al., 2009).
In this paper, as a pre-processing system of our
system, we consider introducing a discrete-time dy-
namical system (Zhao et al., 2003), which functions
as a multi-scaling system (degradation system) for
gray levels of pixels like a K-means technique (Harti-
gan and Wong, 1979), so that it can yield successful
dynamic segmentation for a gray scale image. The
multi-scaling system not only gradate a gray scale
image but also compute the proximity between pix-
els, i.e. their connections, based on their multi-scaled
gray levels concurrently. Computed proximity is sig-
nificant for designing parameter values of our system.
159
Fujimoto K., Musashi M. and Yoshinaga T. (2010).
DYNAMIC IMAGE SEGMENTATION SYSTEM WITH MULTI-SCALING SYSTEM FOR GRAY SCALE IMAGE.
In Proceedings of the Third International Conference on Bio-inspired Systems and Signal Processing, pages 159-162
DOI: 10.5220/0002689701590162
Copyright
c
SciTePress

2 SYSTEM DESCRIPTION
Our dynamic image segmentation system (Fujimoto
et al., 2008) was designed for a binary image. In this
paper, we consider introducing a multi-scaling sys-
tem (Zhao et al., 2003) into our original system so
that it can work well for a gray scale image.
2.1 Multi-scaling System of Gray Levels
In segmentation of a gray scale image, a fundamen-
tal task is to find an image region (connected compo-
nents) that consists of pixels with different gray levels.
As an approach, a multi-scaling technique for a gray
scale image has been proposed (Zhao et al., 2003).
The scheme consists of degradation of a gray scale
image like a K-means technique (Hartigan and Wong,
1979) and concurrent computation of the proximity
between pixels based on their gradated gray levels.
Moreover, it has an interested feature that it needs no
setting of the number of centroids and their initial ar-
rangements unlike the K-means method.
The scheme is performed by utilizing nonlinear
dynamics of the following discrete-time dynamical
system. Let p
i
(τ) be the ith pixel value normalized
in the range [0, 1]. It is updated according to
p
i
(τ+ 1) =
0 if p
i
(τ)+ ηF
i
(τ) ≤ 0
p
i
(τ)+ ηF
i
(τ) if 0 < p
i
(τ)+ ηF
i
(τ) < 1
1 if p
i
(τ)+ ηF
i
(τ) ≥ 1
(1)
and
F
i
(τ) =
1
S
i
(τ)
X
j∈∆
i
(τ)
p
j
(τ)− p
i
(τ)
|p
j
(τ)− p
i
(τ)|
e
−γ|p
j
(τ)−p
i
(τ)|
, (2)
where p
i
(0) is given as the normalized gray level of
the ith pixel in an input image; ∆
i
(τ) denotes a set
of pixels with approximately the same value as p
i
(τ);
and the sign |·| expresses the absolute value. S
i
(τ) rep-
resents the number of elements in ∆
i
(τ) and is counted
based on the proximity level q
ij
(τ) between the ith and
jth pixel values at every iteration. It is updated as
q
ij
(τ + 1) = βq
ij
(τ)+ (1− β)H
e
−γ|p
j
(τ)−p
i
(τ)|
− ψ
,
(3)
where H denotes the Heaviside step function and re-
turns zero or one if its argument value is negative or
non-negative, respectively. η, γ, β, and ψ are positive
parameters, and the each value except for γ is set as
less than one. Therefore, the value of q
ij
(τ) gradu-
ally converges to the return value of H, e.g., q
ij
(τ + 1)
approaches one when the values of p
i
(τ) and p
j
(τ)
are close. Based on the values of q
ij
(τ), the values
of p
i
(τ) are also converged to several clusters gradu-
ally, and eventually, a multi-scale image is obtained.
According to the values of p
i
and q
ij
after sufficient
iteration, couplings between adjacent chaotic neurons
are determined so that the ith and kth chaotic neurons
are coupled only if q
ik
= 1, where k ∈ L(i).
2.2 Coupled System of Chaotic Neurons
Our dynamic image segmentation system (Fujimoto
et al., 2008)consists of a global inhibitor and the same
number of chaotic neurons (Aihara et al., 1990) as
pixels of an input image. A chaotic neuron can gen-
erate an oscillatory response under adequate values of
system parameters. Dynamic image segmentation is
performed based on oscillatory responses.
The architecture of our system and dynamic image
segmentation scheme are illustrated in Fig. 1. Chaotic
neuronsare arranged in a two-dimensionalgrid so that
one corresponds to a pixel. Chaotic neurons corre-
sponding to high-gray-level pixels in an image region
are coupled and also have a positive self-feedback
coupling. The global inhibitor connects to all chaotic
neurons and suppress their activity levels when one
or more chaotic neurons fire. The dynamics of the
ith chaotic neuron with two state variables (x
i
, y
i
) is
described as
x
i
(t+ 1) = k
f
x
i
(t)+ I
i
+ C
i
(t) (4)
y
i
(t+ 1) = k
r
y
i
(t)− αg
(
x
i
(t)+ y
i
(t), 0
)
+ a, (5)
where t denotes the discrete time. I
i
takes a value
from 0 to 2, and we set the value of I
i
as the value
of lim
τ→∞
2p
i
(τ). C
i
(t) represents the sum of exter-
nal stimuli from chaotic neurons including itself in
the same image region and the global inhibitor. It is
described as
C
i
(t) =
X
k∈L(i)
W
M(i)
g
(
x
k
(t)+ y
k
(t), 0
)
− Wg
(
z(t), 0.5
)
,
(6)
where L(i) denotes a set of chaotic neurons corre-
sponding to almost the same gray levels of pixels as
the ith pixel in its four-neighborhood. M(i) is the
number of elements in L(i) and be calculated as the
number of chaotic neurons satisfying q
ik
= 1 in which
k ∈ L(i). g denotes the output function of a chaotic
neuron or the global inhibitor and is defined as
g(u(t), θ) =
1
1+ exp
(
−(u(t)− θ)/ε
)
. (7)
The dynamics of the global inhibitor with a state vari-
able (z) is expressed as
z(t+ 1) = φ
g
N
X
i=1
g
(
x
i
(t)+ y
i
(t), W
)
, 0
− z(t)
, (8)
where N denotes the number of chaotic neurons.
BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing
160
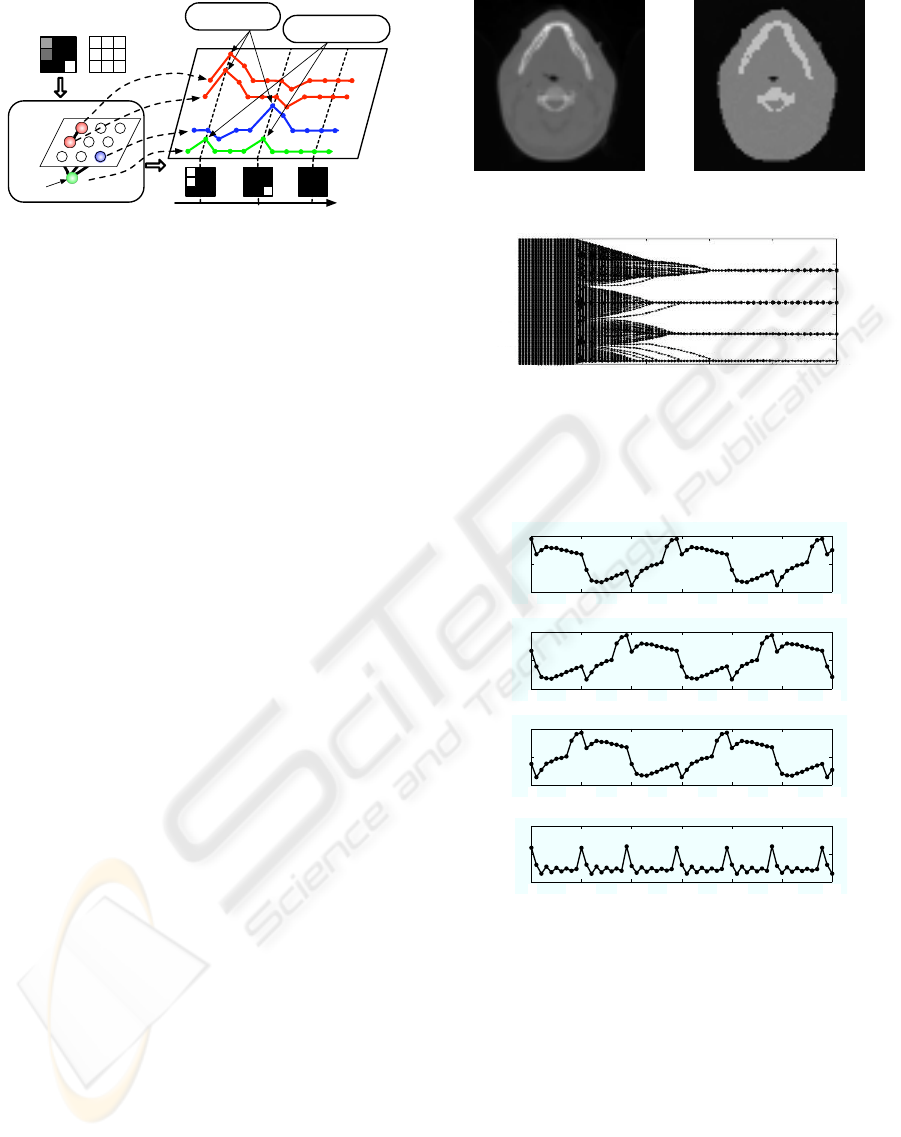
Input image and
index numbers of pixels
Coupled system of
chaotic neurons and a
global inhibitor
Discrete
time
Firing of chaotic
neurons
Output images
Global
inhibitor
1
2
3
4
5
6 9
8
7
Chaotic
neurons
t = t
k−n
t = t
k+n
t = t
k
Firing of the global
inhibitor
Figure 1: System architecture and dynamic image segmen-
tation scheme.
Let us explain dynamic image segmentation
scheme using a multi-scaling system and our system.
Now, we treat a gray scale image with 3 × 3 pixels
shown in Fig. 1. A multi-scaling system provides a
multi-scaled image and connections between pixels in
the processed image. As the results, it has two high-
gray-level image regions: one is composed of the first
and second pixels and the other is the ninth pixel.
Therefore, only the three chaotic neurons can oscil-
late. In addition, based on computed connections, the
first and second chaotic neurons are coupled and can
oscillate in phase. When one or more chaotic neuron
fire, the global inhibitor also fires and suppresses the
activity levels of all chaotic neurons at the next time.
Owing to the suppression, chaotic neurons in different
image regions can fire separately. By assigning high
gray levels to pixels that correspond to fired chaotic
neuron every discrete time, individual segmented im-
ages are output and are exhibited in time series.
3 EXPERIMENTAL RESULTS
We treated an 8-bit computed tomography (CT) im-
age with 64 × 64 pixels at a human head shown in
Fig. 2(a). It is provided from the public database of
the visible human project (Ackerman, 1991). From
visual evaluation for the image, it has one mid-
intensity image region and two isolated high-intensity
image regions. The mid-intensity region corresponds
to soft tissues, the upper high-intensity region denotes
teeth and the mandible bone, and the lower one repre-
sents a cervical spine, roughly.
At first, to obtain a multi-scale image of the
original image, the multi-scaling procedure was
performed, where we set the parameter values in
Eqs. (1)–(3) as η = 0.01, γ = 5, β = 0.1, and ψ = 0.5.
Figure 2(c) shows the multi-scaling process. Its ab-
scissa denotes the iteration number (discrete time) and
(a) 8-bit original image (b) multi-scaled image
0 20 40 60 80 100
0.8
0.6
0.4
0.2
1.0
0
τ −→
p
i
−→
(c) process of multi-scaling.
Figure 2: 8-bit CT image and its multi-scaling based on the
nonlinear dynamics described in Eqs. (1)–(3).
t −→
x
1890
+ y
1890
→
x
1900
+ y
1900
→
!
"
!
#
! $!
%
! &! '!
!#!
!
#!
!
"
!
#
! $!
%
! &! '!
!#!
!
#!
0 20 40 6010 30 50
!
"
!
#
! $!
%
! &! '!
!#!
!
#!
0 20 40 6010 30 50
z −→
x
1490
+ y
1490
→
0
1
0
2
0 30
4
0 50 60
0
0.5
1
0 20 40 6010 30 50
0 20 40 6010 30 50
Figure 3: Oscillatory responses of chaotic neurons and the
global inhibitor.
dots at every discrete time represent the distribution of
all pixel values. Although the normalized pixel val-
ues were distributed throughout [0, 1] at τ = 0, they
gradually converged to four clusters based on the dy-
namics of Eqs. (1)–(3). As the result, we obtained a
multi-scaled image shown in Fig. 2(b). It consists of
four gray-levels and has three high-gray-level image
regions that correspond to the aforementioned image
regions from our visual evaluation.
The next, using our system consisting of 4096
(64 × 64) chaotic neurons and a global inhibitor, dy-
DYNAMIC IMAGE SEGMENTATION SYSTEM WITH MULTI-SCALING SYSTEM FOR GRAY SCALE IMAGE
161
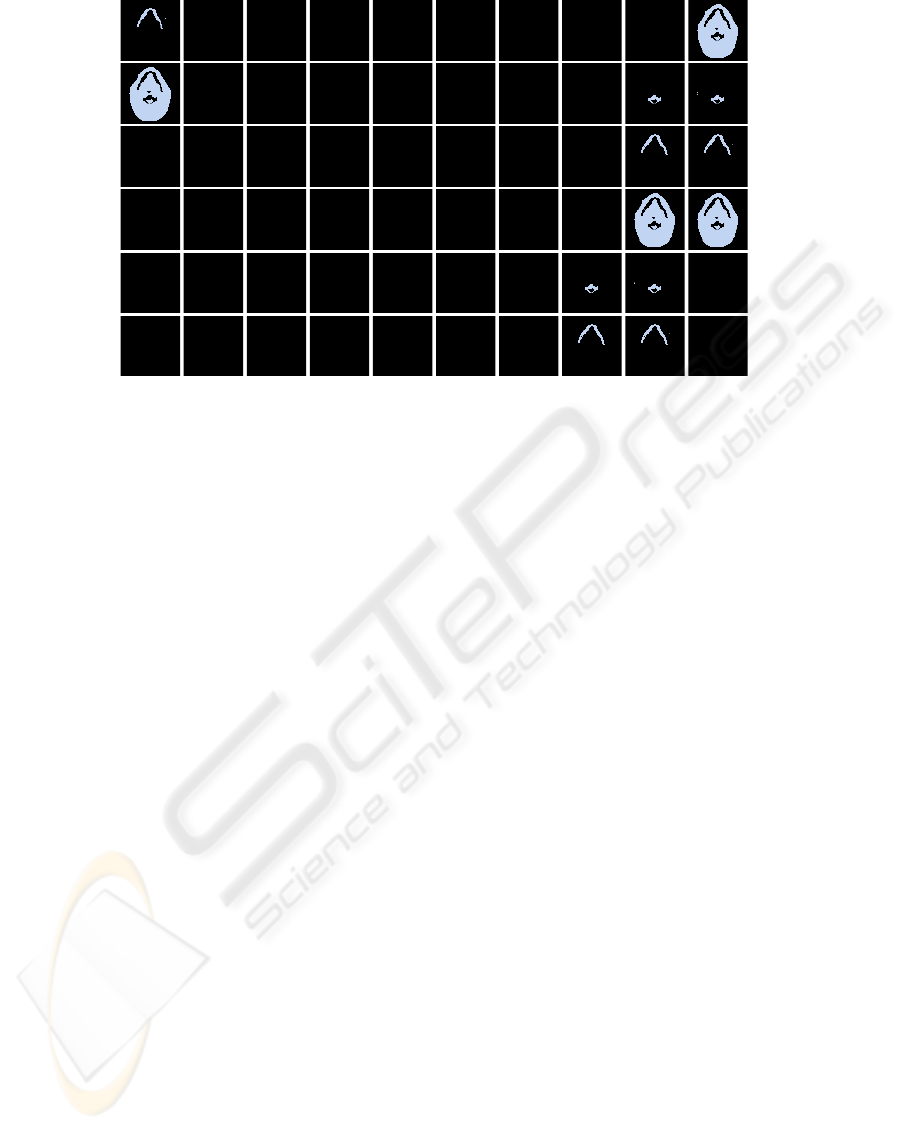
Figure 4: Results of dynamic image segmentation performed by our framework for a gray scale image.
namic image segmentation was performed for the im-
age. According to our analyzed results (Fujimoto
et al., 2009), we set as k
f
= 0.5, k
r
= 0.885, α = 4,
a = 0.5, W = 15, ε = 0.1, φ = 0.8, and I
i
= 2p
i
(100). By
giving certain initial values to all chaotic neurons and
the global inhibitor, chaotic neurons corresponding to
the three image regions oscillated separately in steady
state. Figure 3 shows oscillatory responses of three
chaotic neurons and the global inhibitor. The 1490th,
1890th, and 1900th chaotic neurons correspond to
a part of teeth and the mandible bone, the cervical
spine, and soft tissues, respectively. Moreover, owing
to suppression of the global inhibitor, their oscillatory
responses were out-of-phase each other, i.e., it is a
three-phase oscillatory response. Note that we expe-
diently set the start time of simulation as t = 0.
Figure 4 shows snapshots of dynamically seg-
mented images based on output values of the all
chaotic neurons every discrete time, where the ith
pixel value at t was assigned to 200· g(x
i
(t)+ y
i
(t), W).
The snapshots sequentially appear from the top-left to
the bottom-right. Moreover, their appearances in each
line also start from the left. The three isolated im-
age regions appeared separately, and therefore, it was
demonstrated that our system with a multi-scaling
system worked well for a gray scale image.
4 CONCLUDING REMARKS
We have proposed a dynamic image segmentation
system for a binary image. In this paper, we con-
sidered applying our system to a gray scale image
by introducing a multi-scaling system for gray lev-
els as a pre-processing. Through experiments for a
gray scale image, we demonstrated that the compos-
ite system consisting of the multi-scaling system and
our dynamic image segmentation system works well.
This work was partially supported by the Ministry
of Education, Culture, Sports, Science and Technol-
ogy, Japan, Grant-in-Aid for Young Scientists (B),
No. 20700209.
REFERENCES
Ackerman, M. J. (1991). The visible human project. J.
Biocommun., 18(2):14.
Aihara, K., Takabe, T., and Toyoda (1990). Chaotic neural
networks. Phys. Lett. A, 144(6-7):333–340.
Fujimoto, K., Musashi, M., and Yoshinaga, T. (2008).
Discrete-time dynamic image segmentation system.
Electron Lett., 44(12):727–729.
Fujimoto, K., Musashi, M., and Yoshinaga, T. (2009). Re-
duced model of discrete-time dynamic image segmen-
tation system and its bifurcation analysis. Int. J. Imag.
Syst. Tech. (in Press).
Hartigan, J. A. and Wong, M. A. (1979). A K-means clus-
tering algorithm. Appl. Stat., 28:100–108.
Pal, N. R. and PAL, S. K. (1993). A review on image seg-
mentation techniques. Pattern recognit., 26(9):1277–
1294.
Wang, D. and Terman, D. (1995). Locally excitatory glob-
ally inhibitory oscillator networks. IEEE Trans. Neu-
ral Netw., 6(1):283–286.
Zhao, L., Furukawa, R. A., and Carvalho, A. C. (2003).
A network of coupled chaotic maps for adaptive
multi-scale image segmentation. Int. J. Neural Syst.,
13(2):129–137.
BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing
162
