BRAIN COMPUTER INTERFACE

Application of an Adaptive Bi-stage Classiﬁer based on RBF-HMM

Jos´e Luis Mart´ınez P´erez and Antonio Barrientos Cruz

Grupo de Rob´otica y Cibern´etica, Universidad Polit´ecnica de Madrid, C/Jos´e Gutierrez Abascal 2, Madrid, Spain

Keywords:

Electroencephalography, Brain computer interface, Linear discriminant analysis, Spectral analysis, Biomedi-

cal signal detection, Pattern recognition.

Abstract:

Brain Computer Interface is an emerging technology that allows new output paths to communicate the users

intentions without the use of normal output paths, such as muscles or nerves. In order to obtain their objective,

BCI devices make use of classiﬁers which translate inputs from the users brain signals into commands for

external devices. This paper describes an adaptive bi-stage classiﬁer. The ﬁrst stage is based on Radial Basis

Function neural networks, which provides sequences of pre-assignations to the second stage, that it is based

on three different Hidden Markov Models, each one trained with pre-assignation sequences from the cognitive

activities between classifying. The segment of EEG signal is assigned to the HMMwith the highest probability

of generating the pre-assignation sequence.

The algorithm is tested with real samples of electroencephalograﬁc signal, from ﬁve healthy volunteers using

the cross-validation method. The results allow to conclude that it is possible to implement this algorithm in an

on-line BCI device. The results also shown the huge dependency of the percentage of the correct classiﬁcation

from the user and the setup parameters of the classiﬁer.

1 INTRODUCTION

Since that Dr. Hans Berger discovered the electrical

nature of the brain, it has been considered the possi-

bility to communicate persons with external devices

only through the use of the brain waves (Vidal, 1973).

Brain Computer Interface technology (Wolpaw,

J.R.; et al., 2000) is aimed at communicating with

persons using external computerized devices via the

electroencephalographic signal as the primary com-

mand source (Birbaumer, N; et al., 2000); in the ﬁrst

international meeting for BCI technology it was esta-

blished that BCI “must not depend on the brain’s nor-

mal output pathways of peripheral nerves and mus-

cles” (Wolpaw, J. R.; et al., 2002). The primary uses

of this technology are to beneﬁt persons with block-

ing diseases, such as: Amiotrophic Lateral Sclerosis

(ALS), brainstem stroke, or cerebral palsy; or persons

whom have suffered some kind of traumatic accident

like for example paraplegic (E. Donchin and K. M.

Spencer and R. Wijesinghe, 2000). In order to control

an external device using thoughts, it is necessary to

associate some mental patterns to device commands.

Therefore, an algorithm that detects, acquires, ﬁlters,

and classiﬁes the electroencephalographic signal is

required (Kostov, A.; Polak, M., 2000) (Pfurtscheller

et al., 2000b). Actually different types of classiﬁca-

tions can be established for BCI technology, from the

physiologic point of view BCI devices can be clas-

siﬁed in exogenous and endogenous. The devices in

the ﬁrst group provide some kind of stimuli to the user

and they analyze the user’s responds to them, exam-

ples of this class are devices based on visual evoked

potential or P300 (E. Donchin and K. M. Spencer and

R. Wijesinghe, 2000). On the contrary, the endoge-

nous devices does not depend on the user’s respond to

external stimuli, they base their operationin the detec-

tion and recognition of brain-wave patterns controlled

autonomously by the user, examples of this class are

devices based on the desynchronization and synchro-

nization of µ and β rhythms (Wolpaw, J. R.; et al.,

2002), (Pfurtscheller et al., 2000a), (Pineda, J.A. et

al., 2003).

In this paper is presented an endogenous classi-

ﬁer composed of two adaptive stages. In the ﬁrst

stage a Radial Basis Function neural network (Ripley,

2000) performs a pre-classiﬁcation of the segment of

EEG input signal and provides a pre-assignation se-

quence of data to the second stage. In this second

stage is computed the generation probability of the in-

Luis Martínez Pérez J. and Barrientos Cruz A. (2010).

BRAIN COMPUTER INTERFACE - Application of an Adaptive Bi-stage Classiﬁer based on RBF-HMM.

In Proceedings of the Third International Conference on Biomedical Electronics and Devices, pages 13-20

DOI: 10.5220/0002692700130020

 SciTePress

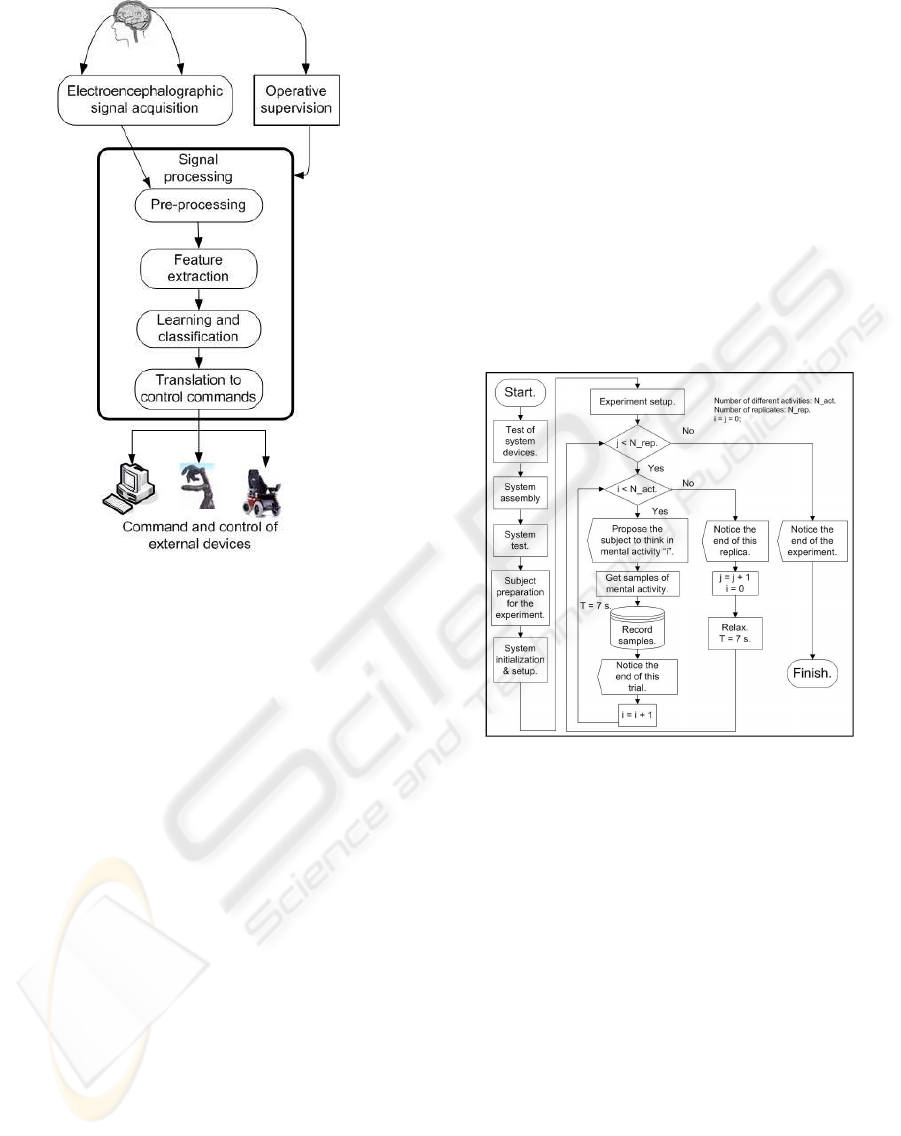
Figure 1: Block diagram of a BCI device.

put sequence by three different Hidden Markov Mod-

els, each one had been previously trained with data

sequences from the different cognitive activities be-

tween classifying.

The content of this paper is as follows:

• Section 2 describes the experimental procedure,

the cognitive activities or mental tasks, and the

equipment to develop the experiment.

• Section 3 presents the proposed two-stage classi-

ﬁer and describes the algorithms employed in it

for training and operation.

• Section 4 presents the results obtained from each

volunteer.

• Section 5 analyzes the previous results.

• And ﬁnally section 6 is devoted to making conclu-

sions.

2 EXPERIMENTAL PROCEDURE

The tests described below were carried out on ﬁve

healthy male subjects, one of whom had been trained

before but the other four of whom were novices in the

use of the system.

In order to facilitate the mental concentration ne-

cessary for the proposed activities, the experiments

were carried out in a room with a low noise level

and under controlled environmental conditions. For

instance, all electronic equipment external to the ex-

periment and unrelated to the subject were switched

off in order to avoid electromagnetic artifacts. The

experiments were carry out between 10:00 a.m. and

14:00 p.m. The subjects were directed to sit down 50

cm from the screen of the acquisition system monitor,

and with their hands in a visible position. The super-

visor of the experiment ensured the correct enactment

of this process.

2.1 Flow of Activities in the

Experimental Process

The experimental process is shown in Figure 2.

Figure 2: Diagram of the experiment carried out.

System Devices Test. The correct battery level and

correct state of the electrodes were checked.

System Assembly. Device connections: superﬁ-

cial electrodes (Grass Au-Cu), battery, bio-ampliﬁer

(g.BSamp by g.tec), acquisition signal card (PCI-

MIO-16/E-4 by National Instrument), computer.

System Test. The correct operation of the whole

system was veriﬁed. To minimize noise from the

electrical network the Notch ﬁlter (50Hz) of the bio-

ampliﬁer was switched on.

Subject Preparation for the Experiment.

Electrodes were applied to the subject’s head.

Electrode impedance ≤ 4KOhms.

System Initialization and Setup. The data register

was veriﬁed. The signal evolution was monitored; it

was imperative that a very low component of 50 Hz

appeared within the spectrogram.

BIODEVICES 2010 - International Conference on Biomedical Electronics and Devices

Experiment Setup. The experiment supervisor set

up the number of replicationsN

rep

= 10, and the quan-

tity of different mentalactivities. The durationof each

trial was t = 7s, and the acquisition frequency was

= 384Hz. The system suggested that the subject

think about the proposed mental activity. A short re-

laxation period was allowed at the end of each trial;

between replications the relax time is t = 7s.

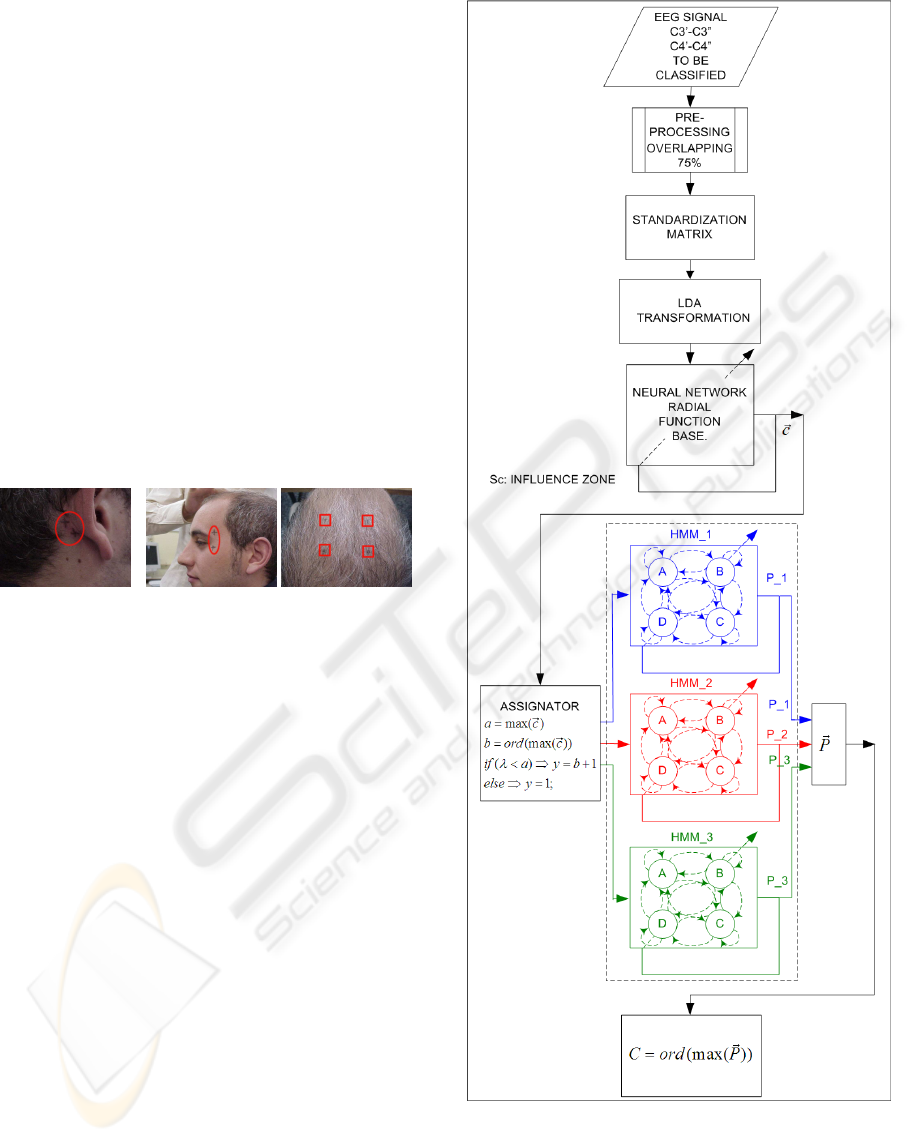
2.2 Electrode Position

Electrodes were placed in the central zone of the

skull, next to C3 and C4 (Penny, W. D.; et al., 2000),

and two pairs of electrodes were placed in front of and

behind the Rolandic sulcus. This zone has the highest

discriminatory power and receives signals from mo-

tor and sensory areas of the brain (Birbaumer, N; et

al., 2000) (Neuper, C.; et al., 2001). A reference elec-

trode was placed on the right mastoid and two more

electrodes were placed near the corners of the eyes to

Figure 3: Electrode placement.

2.3 Description of Cognitive Activities

The experiment supervisor asked the subject to ﬁgure

out the following mental activities; tasks that were

used to differentiate between cerebral patterns (Ne-

uper, C.; et al., 2001):

Activity A. Mathematical task. Recursive subtraction

of a prime number, i.e. 7, from a large quantity, i.e.

3.000.000.

Activity B. Movement task. The subject imagines

moving their limbs or hands, but without actually do-

ing so. It is movement imagery.

Activity C. Relax. The subject relaxes.

3 DESCRIPTION OF THE

CLASSIFIER

3.1 Introduction

In Figure 4 is shown the block diagram of the algo-

rithm for the proposed classiﬁer.

In it can be appreciated how the classiﬁcation of

the considered segment of the EEG signal is obtained

after the evaluation of the probability generation of

Figure 4: Block diagram of the classiﬁer.

the pre-assignation sequence provided by three Hid-

den Markov Models.

There are as many Hidden Markov Models as cog-

nitive activities to be considered for the classiﬁcation,

BRAIN COMPUTER INTERFACE - Application of an Adaptive Bi-stage Classifier based on RBF-HMM

each model is trained with pre-assignation sequences

of data of the cognitive activity associated to it.

The pre-assignation sequence of data are provided

by a neural network, which inputs are the vectors of

features obtained after the preprocessing of the seg-

ment of EEG signal, as it is described in the following

subsections.

3.2 Preprocessing

On Figure 5 is depicted the operations associated to

the preprocessing phase.

In a ﬁrst step the EEG signal coming from both

electroencephalographic channels C3’-C3” and C4’-

C4” are sampled and quantiﬁed at f

= 384Hz.

In the next step the samples are bundled in pack-

age of N

= 128 samples, it is equivalent to T

1/3s. Each group of samples is normalized, in order

to obtain homogenous groups of transformed samples

with zero mean value and unity as standard deviation.

′

− µ

(1)

This transformation does not affect the frequency

properties of the signal, but allows the comparison of

groups of samples in the same session or between ses-

sions, it avoids that changes in the impedance of the

electrodes or skin conductivity affect the next proce-

dures.

After this the samples are processed by a pass

band Butterworth ﬁlter of order n = 6, with lower

and higher frequencies of f

= 4Hz and f

= 40Hz

(Proakis and Manolakis, 1997); frequencies outside

this band are not common in sane conscious users.

In the next step the ﬁltered samples are convoluted

with a Tukey’s window of length N = 128, this ate-

nuates the leakage effect associated to the package

procedure, see Figure 6. Previous studies allow to

conclude that the convolution of the signal with this

kind of window increase the discrimination capabil-

ity that the one obtained with other kind of windows

as for example: rectangular, triangular, Blackman’s,

Hamming’s, Hanning’s or Kaiser’s (Martinez, J.L.;

Barrientos, A., 2006).

After the convolution, the Fast Fourier Transform,

eq.2, is applied in order to obtain the spectral power

estimation, eq.3; the obtained frequency resolution is

in eq.4.

X(k) =

∑

j=1

x( j)w

( j− 1)(k−1)

; w

= e

−

2πi

(2)

P(k) =

X(k)

(3)

∆f =

384

128

= 3Hz (4)

Figure 5: Block diagram for the preprocessing phase.

After the estimation of each frequency band, it is

computed the vector of features consideringthe power

average of the involved bands as it is shown on Table

In case of presence of artifacts the algorithm de-

tects them and during the learning phase it substitutes

its value by the average value of the samples in that

package, if the artifacts are detected in the on-line

phase, it instructs the classiﬁer to discard that group

of samples.

A group of samples is considered with artifacts

if one sample differs more than three standard de-

viations from the previous one.

BIODEVICES 2010 - International Conference on Biomedical Electronics and Devices

Table 1: Feature vector.

Index Denomination. Frequency (Hz).

1 θ. 6 - 8

2 α

. 9 - 11

3 α2. 12 - 14

4 β

. 15 - 20

5 β

. 21 - 29

6 β

. 30 - 38

Figure 6: Frequency leakage effect.

3.3 Training of the Neural Network

The considered neural network is the type of Radial

Function Basis. Thistype of neuralnetwork is charac-

terized by the learning of the position of the samples

in the training set and by the interpolation capability

between them (Ripley, 2000).

In Figure 7 is represented the architecture of this

type of neural network.

Figure 7: Architecture of the RBF neural network.

From previous studies it has been concluded that

this type of neural network behaves better than other

types of neural networks, as for example Multi-Layer

Perceptrons or Probabilistic Neural Networks (Mar-

tinez, J.L.; Barrientos, A., 2008).

The activation function is:

radbas(x) = e

−x

; x = (~w−~p) ∗ S

(5)

In where ~w and S

are respectively the weights and

inﬂuence zone constant of each neuron, and ~p is the

position of the considered sample.

During the learning phase the neurons of the hid-

den layer learn the position of the samples of the

learning set, ~w; during the test phase when a new sam-

ple~p is presented, it is computed the distancebetween

the sample and the learned positions, the nearest neu-

rons to the samplewill proportionate higheractivation

values than the rest of the neurons.

For the learning process are considered vectors of

features from the EEG signal, acquired when the user

was performing one of the different cognitive activi-

ties considered for the classiﬁcation. The learning set

is composed by the 75% of all the sample set, and the

other 25% is considered for validation. After the de-

termination of the learning and validation sets, the in-

put vectors to the neural network are normalized, and

with LDA technique is reduced their dimensionality

projecting the original input vectorsin the direction of

the highest discrimination capability (Martinez, J.L.;

Barrientos, A., 2007).

In order to minimize the over-learning effect, the

RBF learning process allows a dynamic growth of the

number of neurons in the hidden layer. In the out-

put layer are considered as many linear neurons as

cognitive activities between discriminate. Finally in

the assignation block on Figures 4, it is weighted the

output vector of the neural network and it assigns the

input vector to the activity with highest output value

provided it is higher than a threshold λ, on the con-

trary if the value is lower than λ, the input vector is

labeled as unclassiﬁed.

On operation, once the neuronal network has been

trained, when a new vector is presented the cogni-

tive activity, with samples nearer to it, will provide

a higher activation level, and the corresponding out-

put will have a higher value than the others cognitive

activities.

3.4 Description of Hidden Markov

Models

A Hidden Markov Model is a double stochastic sta-

tistical model, it consists of a Markov process with

unknown and non-observable parameters, and a ob-

served model which parameters depend stochastically

from the hidden states. A stochastic processis called a

Markovian process if the future does not depend from

the past, onlyfrom the known present; consideringthe

stochastic variable q(t − 1) the transition probability

in the instant t is deﬁned as P(q

= σ

t−1

= σ

t−1

). A

Markov chain is formally deﬁned with the pair (Q,A),

where Q = {1,2, ..., N} are the possible estates of the

chain and A = [a

] is the transition matrix of the

model, with the constrains:

BRAIN COMPUTER INTERFACE - Application of an Adaptive Bi-stage Classifier based on RBF-HMM

Figure 8: Training of the RBF neural network.

0 ≤ a

≤ 1; 1 ≤ i, j ≤ N (6)

∑

j=1

= 1; 1 ≤ i ≤ N (7)

The transition and emission probabilities depends

from the actual estate and no from the former estates.

P(q

= j|q

t−1

= i,q

t−2

= k,...) = (8)

= P(q

= j|q

t−1

= i) = a

(t)

Formally a discrete HMM of ﬁrst grade is deﬁned

by the 5-tuple: λ = {Z,Q,A,B, π}, in where:

• Z = {V

,...,V

} is the alphabet or discrete set

of M symbols.

• Q = {1,2,...,N} is the set of N ﬁnite estates.

• A = [a

] is the transition matrix of the model.

• B = (b

))

NxM

is the matrix of emission sym-

bols, also known as observation matrix.

• π = (π

,π

,...,π

) is the prior probability vector

of the initial estate.

The parameters of a HMM are λ = {A,B,π}.

There are three types of canonic problems associated

to HMM (Rabiner, 1989)(Rabiner and Juang, 1986):

1. Given the parameters of the model, obtain the

probability of a particular output sequence. This

problem is solved through a forward-backwards

algorithm.

2. Given the parameters of the model, ﬁnd the most

probable sequence of hidden estates, that could

generate the given output sequence. This problem

is solved through the use of Viterbi algorithm.

3. Given an output sequence, ﬁnd the parameters of

the HMM. This problem is solved through the use

of Baum-Welch algorithm.

The HMM have been applied specially in speech

recognition an generally in the recognition of tempo-

ral sequences, hand written, gestures, and bioinfor-

matics (Rabiner and Juang, 1986).

3.5 Training of the Hidden Markov

Models

The HMM’s are trained with sequences of pre-

assignations coming from the EEG samples, as it is

shown in the Figure 9.

For each cognitive activity a particular HMM,

with the following characteristics, is trained:

• Number of hidden estates: 4.

• Number of different observable objects: 4

In the training phase, chains of nine pre-

assignations were used. In a previous experiment

with synthetic samples, it was concluded that for the

proposed architecture of Hidden Markov Models the

highest percentage of correct classiﬁcations were ob-

tained with chains of nine elements.

After the training or solution of the third canonic

problem, the probability matrices of state transitions

and observation matrices are determined. The Viterbi

algorithm is used in order to determine the probability

that a model generates the proposed sequence.

4 RESULTS

In order to test the behavior of the proposed algo-

rithm, the inﬂuence of the threshold assignation pa-

rameter (λ), and the inﬂuence zone of the neuron (S

the EEG samples of the session tests from the volun-

teers were used as follows:

4.1 Evaluation of the Learning

Capability

With a subset of 75% of the all EEG samples the al-

gorithm was trained with different λ and S

values:

BIODEVICES 2010 - International Conference on Biomedical Electronics and Devices

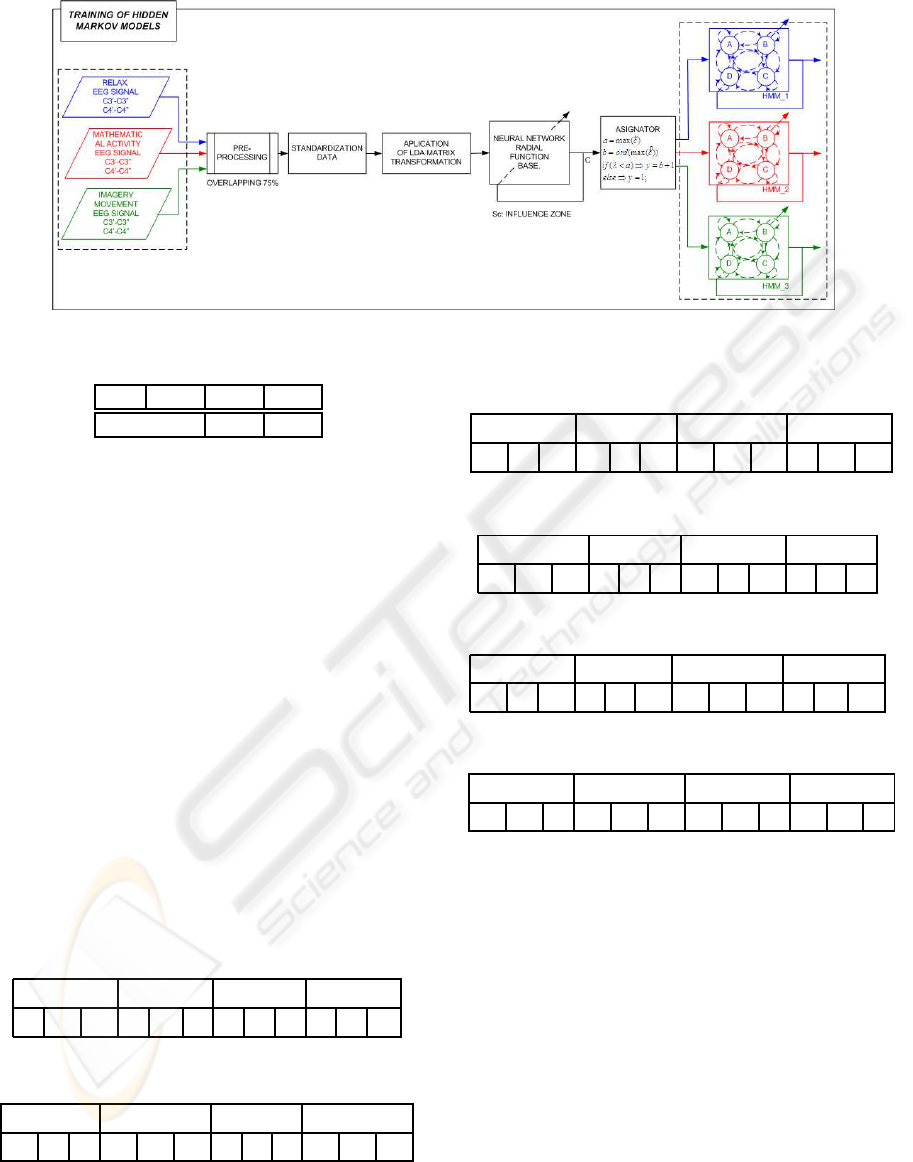
Figure 9: Training of the HMM.

λ = 0.55 0.65 0.8

= 0.5 0.95

These values have been ﬁxed after a seek in wide

with the samples of the ﬁrst volunteer.

After the learning, the same samples were pro-

cessed with the trained algorithm, and a comparison

between the results obtained with the algorithm and

the ones employed for the learning was done, in all

cases a 100% of correct classiﬁcation has been ob-

tained.

4.2 Evaluation of the Generalization

Capability

After the good results obtained from the learning

phase, a cross-validation methodology is used to es-

timate the generalization capability. From the whole

ten sessions, nine are used for learningand one is used

for validation, the process is repeated ten times chang-

ing each time the session used for validation.

In the following tables are shown the results ob-

tained for each volunteer, considering the λ and S

parameters.

Table 2: Volunteer: Al01.

= 0.5 S

= 0.95 S

= 0.5 S

= 0.95

λ = 0.65 λ = 0.55 λ = 0.55 λ = 0.80

94 103 103 94 81 87 93 92 87 86 97 81

+4 +14 +14 +4 -10 -3 +3 +2 -3 -4 +8 -10

Table 3: Volunteer: Ro01.

= 0.5 S

= 0.95 S

= 0.5 S

= 0.95

λ = 0.65 λ = 0.55 λ = 0.55 λ = 0.80

103 97 92 118 109 118 97 87 86 117 106 110

+14 +8 +2 +31 +21 +31 +8 -3 -4 +30 +18 +22

For each combination, the process is replicated

three times. In the upper row it is shown the num-

ber of correct classiﬁcations. In the lower row it is

Table 4: Volunteer: Ja01.

= 0.5 S

= 0.95 S

= 0.5 S

= 0.95

λ = 0.65 λ = 0.55 λ = 0.55 λ = 0.80

106 97 110 87 90 107 99 106 107 98 108 99

+18 +8 +22 -3 0 +19 +10 +18 +19 +9 +20 +10

Table 5: Volunteer: Da01.

= 0.5 S

= 0.95 S

= 0.5 S

= 0.95

λ = 0.65 λ = 0.55 λ = 0.55 λ = 0.80

109 102 104 83 92 92 106 91 110 86 87 92

+21 +13 +15 -8 +2 +2 +18 +1 +22 -4 -3 +2

Table 6: Volunteer: Ra01.

= 0.5 S

= 0.95 S

= 0.5 S

= 0.95

λ = 0.65 λ = 0.55 λ = 0.55 λ = 0.80

106 97 110 87 90 107 99 106 107 91 76 99

+18 +8 +22 -3 0 +19 +10 +18 +19 +1 -15 +10

Table 7: Volunteer: Ra02.

= 0.5 S

= 0.95 S

= 0.5 S

= 0.95

λ = 0.65 λ = 0.55 λ = 0.55 λ = 0.80

102 102 98 102 107 114 103 105 96 116 99 98

+13 +13 +9 +13 +19 +26 +14 +16 +6 +29 +10 +9

shown the percentage of improvement against a naive

classiﬁer.

5 DISCUSSION

From the results of the proposed classiﬁcation algo-

rithm, it is observed that:

• The learning capability is better that the one

achieved only with the RBF neural network (Mar-

tinez, J.L.; Barrientos, A., 2008).

• From the analysis of the results of the replicas

it has been detected that the variability in the

percentage of correct classiﬁcations is caused by

the HMM’s, both in the learning and validation

phases. The sequences of pre-assignations pro-

BRAIN COMPUTER INTERFACE - Application of an Adaptive Bi-stage Classifier based on RBF-HMM

vided by the neural network were stable, but the

generation probabilities of the HMM’s changed in

each replica. In the learning phase the HMM’s

probabilities allowed a perfect classiﬁcation, but

they were not maintained in the cross validation

phase; for this stage a lower percentage of correct

classiﬁcation was obtained, as it is summarized in

the tables 2 to 7. But until in this case, almost in

all replicas, the cross-validation test results were

better than the ones hoped from a naive classiﬁer.

• The values of correct classiﬁcations depend

highly from the user. There has not been identi-

ﬁed a pair of λ and S

values which proportionate

the highest percentage of correct classiﬁcation for

all users. The discrepancy in the results between

RA1 and RA2 is explained by the user’s learning

process, session RA1 is previous to RA2.

6 CONCLUSIONS

The information inside the pre-assignation sequences

improves the classiﬁcation capability, therefore the

Hidden Markov Model technique is useful for the ex-

traction and use of this information in an On-line BCI

device.

The scattering of the maximum values, of the cor-

rect classiﬁcations obtained from the cross-validation

tests, shows that the combination of λ and S

param-

eters are highly dependent on the user, for this reason

a BCI device based in this kind of algorithm should

have a setup stage, that allows to initialize correctly

these parameters.

On the other hand, the algorithm behaves better

than a naive algorithm, but it is not as good as it

should be taking into account the good results ob-

tained during the learning phase. The size of the

learning data set is critical in the results obtained dur-

ing the validation phase. With a bigger learning data

set the validation results will improve, because of the

minimization of the overlearning.

In future applications the algorithm presented in

this paper will be used as kernel for an on-line classi-

ﬁer embedded in a BCI device. The on-line use of this

device will allow to assess how the different kinds of

user’s feedbacks modify the classiﬁcation capability.

REFERENCES

Birbaumer, N; et al. (2000). The thought translation de-

vice (TTD) for completely paralyzed patients. IEEE

TRANS. ON REH. ENG., 8(2):190–193.

E. Donchin and K. M. Spencer and R. Wijesinghe (2000).

The mental prosthesis: assessing the speed of a p300-

based brain-computer interface. IEEE Transactions

on Rehabilitation Engineering, 8(2):174–179.

Kostov, A.; Polak, M. (2000). Parallel man-machine

training in development of EEG-based cursor control.

IEEE TRANS. ON REH. ENG., 8(2):203–205.

Martinez, J.L.; Barrientos, A. (2006). The windowing Ef-

fect in Cerebral Pattern Classiﬁcation. An Application

to BCI Technology. IASTED Biomedical Engineering

BioMED 2006, pages 1186–1191.

Martinez, J.L.; Barrientos, A. (2007). Linear Discriminant

Analysis on Brain Computer Interface. 2007 IEEE. In-

ternational Symposium on Intelligent Signal Process-

ing. Conference Proceedings Book., pages 859–864.

Martinez, J.L.; Barrientos, A. (2008). Brain computer inter-

face. comparison of neural networks classiﬁers. Pro-

ceedings of the BIODEVICES International Confer-

ence on Biomedical Electronics and Devices., 1(1):3–

10.

Neuper, C.; et al. (2001). Motor Imagery and Direct Brain-

Computer Communication. Proceedings of the IEEE,

89(7):1123–1134.

Penny, W. D.; et al. (2000). EEG-based communication: A

pattern recognition approach. IEEE TRANS. ON REH.

ENG., 8(2):214–215.

Pfurtscheller et al. (2000a). Brain oscillations control

hand orthosis in a tetraplegic. Neuroscience Letters,

1(292):211–214.

Pfurtscheller et al. (2000b). Current trends in Graz brain-

computer interface (BCI) research. IEEE TRANS. ON

REH. ENG., 8(2):216–219.

Pineda, J.A. et al. (2003). Learning to Control Brain

Rhythms: Making a Brain-Computer Interface Pos-

sible. IEEE TRANS. ON REH. ENG., 11(2):181–184.

Proakis, J. G. and Manolakis, D. G. (1997). Tratamiento

digital de se˜nales : [principios, algoritmos y aplica-

ciones]. Prentice-Hall, Madrid.

Rabiner, L. R. (1989). A tutorial on hidden markov models

and selected applications in speech recognition.

Rabiner, L. R. and Juang, B. H. (1986). An introduction to

hidden markov models.

Ripley, B. (2000). Pattern Recognition and Neural Net-

works. Cambridge University Press, London, 2nd edi-

tion.

Vidal, J. J. (1973). Toward direct brain-computer commu-

nication.

Wolpaw, J. R.; et al. (2002). Brain-Computer interface for

communication and control. Clinical Neurophysiol-

ogy, 113:767–791.

Wolpaw, J.R.; et al. (2000). Brain-Computer Interface Tech-

nology: A Review of the First International Meeting.

IEEE TRANS. ON REH. ENG., 8(2):164–171.

BIODEVICES 2010 - International Conference on Biomedical Electronics and Devices