PATIENT JOURNEY OPTIMIZATION USING A MULTI-AGENT

APPROACH

Chung-ho Choi, William K. Cheung, Jiming Liu

Department of Computer Science, Hong Kong Baptist University, Hong Kong

Ian T. Cheung

Quality and Safety Division, Hospital Authority, Hong Kong

Keywords:

Multi-agent systems, Patient journey optimization, Scheduling algorithms, Health information systems.

Abstract:

With the increasing expectation from patients and the regulations enacted by the government, exploring ways

to shorten patient journey has caught increasing attention. Patient journey optimization typically involves

the coordination of treatment scheduling at multiple medical units. This decentralized nature of the problem

makes conventional centralized operation research methods hard to be applied and motivates the use of the

multi-agent approach. In this paper, we focus on cancer patient treatment. We model patients and medical

units as autonomous agents which interact locally via a bidding process and a coordination process for patient

journey optimization. With reference to a dataset containing more than ﬁve thousand cancer patient journeys,

the effectiveness of the proposed algorithm under different settings of implementation has been evaluated via

experimental simulations.

1 INTRODUCTION

Shortening the length of patient journey with unnec-

essary waiting time avoided is always an expectation

of patients. Also, it is one of the key performance in-

dicators for evaluating the effectiveness of healthcare

providers. In order to raise the standard for health-

care services, careful application of scheduling al-

gorithms is crucial (Vermeulen et al., 2006). While

conventional operations research methods have been

found effective for scheduling-related problems (Vis-

sers et al., 2005; Patrick and Puterman, 2008), most

of them take the centralized approach and are not de-

signed to be applied to decentralized situations (Ver-

meulen et al., 2006; Decker et al., 2000).

The multi-agent approach is characterized by em-

phasizing on local interaction and self-organization

of different entities being modeled. These proper-

ties make it especially suitable for tackling complex

tasks with a lot of stakeholders involved and the envi-

ronment is dynamic (Czap and Becker, 2003). Multi-

agent methods have found applications in a variety of

problem domains, such as airport resource schedul-

ing (Mao et al., 2007), load allocation in transporta-

tion logistics (Robu et al., 2008), supply chain man-

agement (Wang et al., 2008), etc. Recently, it has

also been applied to patient scheduling in (Paulussen

et al., 2003; Vermeulen et al., 2006) with some ini-

tial success demonstrated. And yet, there are lim-

itations. Paulussen et al. (Paulussen et al., 2003)

assumed that a health state can be accurately quan-

tiﬁed as utility measure for guiding the scheduling

process. Vermeulen et al. (Vermeulen et al., 2006)

assumed that temporal constraints between treatment

operations need not be considered during the schedul-

ing process.

The objective of this study is to explore the extent

to which patient journey can be improved by better

coordinating and mobilizing resources distributed at

different medical units. In particular, we formulate

the scheduling problem according to the cancer treat-

ment practice in Hong Kong. We propose the use of

a multi-agent approach in which autonomous agents

interact with each other to arrive an effective over-

all schedule with reduced waiting times. To evaluate

the effectiveness of the proposed approach, we have

carried out simulations with the proposed approach

given different settings of the environment. To initial-

ize the simulation environment, we made use of a pa-

tient identity anonymized data set collected by Hospi-

181

Choi C., K. Cheung W., Liu J. and T. Cheung I. (2010).

PATIENT JOURNEY OPTIMIZATION USING A MULTI-AGENT APPROACH.

In Proceedings of the Third International Conference on Health Informatics, pages 181-186

DOI: 10.5220/0002693901810186

 SciTePress

tal Authority in Hong Kong which contains 5819 can-

cer patient journeys with the admission period span-

ning over 6 months.

The rest of the paper is organized as follows. The

patient scheduling problem formulation is described

in Section 2. Sections 3 and 4 present the details of the

proposed agent-based scheduling algorithm. Section

5 presents some preliminary experimental results and

Section 6 concludes the paper.

2 PROBLEM FORMULATION

In this section, we ﬁrst brieﬂy describe the establish-

ment of the cancer clusters in Hong Kong. Then, we

formulate the patient scheduling problem for cancer

treatment as an optimization problem.

2.1 Cancer Patient Treatment - A Hong

Kong Scenario

In Hong Kong, there are seven cancer clusters estab-

lished and we denote them as C = {C

, C

, ..., C

Currently, on-demand information exchange among

the clusters for patient scheduling is not yet exten-

sively used. That is why it is common for cancer pa-

tients to be scheduled to receivetreatments at only one

cancer cluster, even though some of the treatments

could be provided earlier by other clusters.

Generally speaking, once a patient is suspected to

have cancer, the doctor will specify the patient a treat-

ment plan which contains a sequence of treatment op-

erations. We denote the set of treatment operations as

Γ = {radiotherapy, surgery, chemotherapy}.

To carry out the treatment operations, medical re-

sources are needed. We denote the set of medical re-

sources (or units) as A = {radiotherapy unit, operation

unit, chemotherapy unit}. We assume that one treat-

ment operation can only be performed at one medical

unit of the corresponding type. A patient journey is

deﬁned as the duration from the date of admission to

the date of the last treatment operation completed.

2.2 Formulation

Let K := A × C be the cartesian product of A and C

giving the complete set of medical units, M := K → Γ

be an one-to-one mapping between K and Γ specify-

ing the treatment type of the medical units, and P be

the set of cancer patients being scheduled.

Also, given a patient i, let N

denote the number of

treatment operations needed, D

denote the admission

date, D

denote the date of the j

treatment operation

where 1 ≤ j ≤ N

, V

∈ K be the unit at which the

treatment operation is performed, Tr

∈ Γ be the

type of treatment for the j

operation,C

be the daily

capacity (i.e. number of patients that could be treated)

of medical unit k ∈ K, T

be the duration (in days)

of treatment type t ∈ Γ, and Z be the set of dates on

which patient scheduling is being considered.

With the assumption that all the patients are be-

ing treated equally in terms of urgency, the scheduling

problem can be formulated as:

min

|P|

∑

i=1

−1

∑

j=1

(|D

− D

j+1

|) (1)

with the following constraints to be satisﬁed:

j+1

> D

+ T

(2)

∀d ∈ Z



{i : D

= d ∧V

= k∧ Tr

= M(k)}



≤ C

(3)

> D

> 0 (4)

The objective function in (1) is to minimize the

time lags between treatment operations for cancer pa-

tients. Constraint (2) ensures the temporal constraints

between treatment operations are not violated, con-

straint (3) is used to ensure all medical units are op-

erating within their capacities. Constraint (4) ensures

that patients would only be scheduled to receive treat-

ment operations after their admissions.

3 SCHEDULING FRAMEWORK

Theoretically, patient waiting times could be mini-

mized by optimizing (1). However, it is impractical

to do so as it is hard to assume that a cancer clus-

ter is willing to share its real-time resource allocation

related data (e.g., C

) with other clusters due to both

technical and managerial reasons.

Hence, in this section, we propose the use of a

multi-agent approach for our domain. Particularly,

in our proposed framework, there are two types of

agents, namely patient agents and resource agents.

3.1 Patient Agent

A patient agent is used to represent one cancer patient

and is denoted as P

with i = 1, 2, ..., |P|. It stores the

patient’s treatment plan. As it is common that some

treatment operations have to be performed in prior to

another, the set of treatment operations to be received

by a patient has to satisfy certain temporal constraints.

Hence, each patient agent P

maintains an ordered set

= {Tr

, Tr

, ...Tr

} as its treatment plan.

HEALTHINF 2010 - International Conference on Health Informatics

182

3.2 Resource Agent

A resource agent is used to manage a speciﬁc medical

unit. Here, we denote R

as a resource agent rep-

resenting medical unit a ∈ A at cancer cluster b ∈ C .

Each resource agent has full access to the schedule of

the medical unit it represents, but not the others.

3.3 Scheduling Algorithm

We adopt a two-phase scheduling algorithm similar to

what being proposed in (Paulussen et al., 2003; Ver-

meulen et al., 2006). For each newly admitted patient,

a treatment plan is ﬁrst designed and then the corre-

sponding treatment operations are initially scheduled

(initial assignment phase). Then, a timeslot-swapping

process is enforced for shortening the patient jour-

ney (rescheduling phase). Here we assume that any

two patient agents are willing to exchange their times-

lots as far as none of their schedules is worsen (as

suggested in (Vermeulen et al., 2006)) and none of

the temporal constraints as speciﬁed in Eq.(2) is vio-

lated.

4 AGENT COORDINATION

In this section, more details about the scheduling al-

gorithm are given, including 1) how the patient agents

interact with the resource agents, and 2) how some

“unnecessary” swappings can be rejected so as to fur-

ther improve the scheduling optimality.

4.1 A Bidding Process for Agent

Matchmaking

Figure 1 shows our proposed framework. As what

have been introduced earlier, there are two types of

agents, namely patient agents and resource agents.

In order to show clearly the coordination between

agents, we further categorize patient agents into ini-

tiating patient agents and target patient agents. Ini-

tiating patient agents P

are those patient agents who

initiate a request for timeslot exchange while target

patient agents P

are those who are willing to partic-

ipate in the exchanging process.

In order to shorten its patient journey, an initiat-

ing patient agent P

would ﬁrst send out a request

for rescheduling to the corresponding resource agents

This assumption may imply that some policy-wise in-

centive has to be in place so that different medical units are

willing to share their resources in this manner, which how-

ever is not the main focus of our study.

Figure 1: The proposed agent coordination framework for

patient scheduling.

. The request includes the earliest possible start

date (EPS) and the latest possible start date (LPS) of

its associated treatment operation. In order not to vi-

olate the temporal constraints between treatment op-

erations, the EPS can be deﬁned as:

EPS

= D

j− 1

+ T

j−1

+ δ

. (5)

Note that δ

denotes how many days a patient should

be admitted (if needed) before a treatment operation

to be carried out. In our experiment, we set to be 1. In

practice, this value could be designated by healthcare

providers. With a similar argument, LPS is deﬁned as:

LPS

= D

− 1. (6)

Once a resource agent receivesa request with EPS

and LPS, it will ﬁrst check whether there are avail-

able timeslots released by deceased patients. If yes,

the released timeslot will be assigned to the initiat-

ing patient agent. If not, the resource agent will then

pass the request to those patient agents (target patient

agents, P

) which reserved resources of the same type

in the period from EPS to LPS. Those target patient

agents who have received the request will submit a

bid to the resource agent in response.

There are several factors needed to be considered

in computing the bid value.

• The target patient agent should not have its last

treatment operation to be exchanged; otherwise,

it would end up with a lengthened journey.

• As it is impractical to reschedule a patient’s treat-

ment operation without prior notiﬁcation, we as-

sume that the exchange of timeslots would not

be considered if the patient will have less than a

PATIENT JOURNEY OPTIMIZATION USING A MULTI-AGENT APPROACH

183

week’s time of notiﬁcation.

• The target patient agent has to ensure that the tem-

poral constraints between its treatment operations

would not be violated after the exchange.

Taking into account the above considerations, the

bid value submitted by P

is formulated as:

Bid

= (D

− EPS

) + Last + Noti+ Temp, (7)

where Last, Noti and Temp are three binary variables.

Last = 0 if the j

th operation is not the last one for P

or ∞ otherwise. Noti = 0 if a week’s time of notiﬁca-

tion for the target patient agent to be notiﬁed, or ∞

otherwise. Temp = 0 if there are no temporal con-

straints violated, or ∞ otherwise.

Among all the target patient agents, the one with

the lowest bid value will be accepted and the timeslot

swapping between P

and P

will be conﬁrmed. If

two bids are found to be numerically identical, the

resource agent will select one at random.

4.2 A Coordination Process for

Rejecting Unnecessary Swappings

A timeslot swapping conﬁrmed as described in the

previous section does not necessarily lead to a short-

ened patient journey. To illustrate that, suppose there

is a patient agent with 3 treatment operations to be

rescheduled. In case the last treatment operation

could not be rescheduled to be performed earlier, any

rescheduling of the ﬁrst 2 are useless as the dura-

tion of the whole journey remains unchanged (see

Figure 2(a)). As another example, even a shortened

patient journey can be achieved, rescheduling of the

ﬁrst 2 treatment operations could also be useless if the

rescheduling of the last one cannot be beneﬁted from

the rescheduling of the ﬁrst two (see Figure 2(b)).

In order to eliminate these useless swappings, a

resource agent after identifying the most optimal bid

among the target patient agents will not notify the

initiating patient agent immediately. Instead, it will

pass the bid to the resource agent which is responsi-

ble for the succeeding treatment operation of the ini-

tiating patient agent. Having received such a bid, the

resource agent could derive a new EPS, denoted as

(new)

EPS

. Clearly, unnecessary swappings occur

if that resource agent could not ﬁnd a bid such that

(new)

EPS

≤ D

′

≤ EPS

, where Tr

= Tr

′

In that case, the resource agent will notify its an-

tecedent to discard the bid such that the corresponding

timeslots would not be exchanged.

In general, the time of notiﬁcation can be adjusted ac-

cording to the real situation.

Figure 2: Unnecessary reschedulings.

5 EXPERIMENTAL VALIDATION

To evaluate the effectiveness of the proposed multi-

agent approach, we ﬁrst obtained a dataset containing

5819 cancer patients who were treated at the 7 cancer

clusters in Hong Kong within an admission period of

6 months. The average length of the patient journey

among all cancer clusters is 90.7 days. Based on the

dataset, we had carried two groups of simulation.

For the ﬁrst group of simulation, we made use

of the scheduled treatment plans in the dataset for

the initial assignment and studied to what extent the

multi-agent approach can improve the patient journey

as a whole.

For the second group of simulation, we aim to

make the simulation more ﬂexible by making use of

only the statistics of the scheduled treatment plans

and the capacities of the medical units as revealed in

the dataset. The initial assignment strategy and the

reschedulingstrategy can both be speciﬁed by the user

for evaluation. Also, we tried to increase the capacity

value as revealed in the dataset by percentage so as to

see to what extent the patient journeycan be improved

with more resources injected.

5.1 Simulation with Initial Assignment

and Unit Capacity Fixed (Exp. A)

Four different settings had been used to demonstrate

various aspects of the proposed algorithm:

Setting 1: Patient agents are willing to exchange

timeslots with others whenever there is a Pareto

improvement.

Setting 2: It is assumed that only 20% of the pa-

tients of each cancer cluster are allowed to un-

dergo timeslot swapping.

HEALTHINF 2010 - International Conference on Health Informatics

184

Setting 3: It is assumed that only swappings between

two nearby cancer clusters are allowed.

Setting 4: Timeslots released by deceased patients

are allocated to the patient agents who have the

longest patient journeys at a time point.

Given the four aforementioned settings, Figure 3a

shows the average length of the patient journeys asso-

ciated with the seven cancer clusters in Hong Kong.

Figure 3: a) Average length of patient journey; b) Maximum

length of patient journey among the seven cancer clusters in

Hong Kong under 4 different settings in Exp. A.

The experimental results obtained show that, on

average, the average length of journey can be re-

duced by 9.8 days for those 5819 cancer patients if

no restriction is imposed on the exchange of times-

lots whenever there is a Pareto improvement (Setting

1). Given only 20% of patients per cancer cluster are

allowed for timeslot exchange (Setting 2), we found

that the average length of journey could still be re-

duced by an average of 6.1 days. With the geograph-

ical restriction on allowing only swappings between

nearby cancer clusters (Setting 3), the average length

of journey can also be reduced by 9.3 days.

However, it should also be noted that according to

Figure 3b, the maximum length of journey remains

unchanged. The reason is obvious as no one is will-

ing to swap with those with the longest length of jour-

ney. Reductions on the maximum length of journey

can only be observed for Setting 4 where the released

timeslots due to deceased patients are allocated to

those with the longest journey.

5.2 Simulation Revealing the Effects of

Varying Initial Assignment and Unit

Capacity (Exp. B)

Contrary to the group of simulation previously pre-

sented, we tried to simulate also the initial assign-

ment process using again the treatment plans of the

5819 cancer patients. However, all the treatment op-

erations were not scheduled according to the data but

simulated based on the statistics of the inter-operation

duration obtained from the dataset. In particular, dur-

ing the initial assignment phase, patient agents would

be assigned an initial schedule one by one based on

their admission orders. For each treatment operation,

each patient agent would be assigned with the next

earliest available timeslot. However, it is obvious that

there should be a minimum time lag between two sub-

sequent treatment operations due to different medical

reasons. We ﬁrst used the average inter-operation du-

ration computed based on the dataset and then per-

formed the simulation. The average length of jour-

ney computed right after the initial assignment was

found to be 83.3 days. The improvements obtained

due to the different settings are not very much differ-

ent from those obtained in the previous section. Due

to the page limit, we would not show them here.

According to the dataset, the minimum days be-

tween any two treatment operations was found to be

one only. This implies that treatment operation some-

times could be started one day after another if the re-

source is available. We had also tried to set the mini-

mum days to one in our initial assignment phase and

compared with the results obtained before. According

to Figure 4, while we observed some improvements

in performance, the enhancement however is not very

signiﬁcant. Hence, setting some reasonable time lags

between treatment operations does not have too big

an impact on lengthening the patient journey.

For all the results presented so far, it is assumed

that the capacity of each medical unit is ﬁxed. To

study the cost-effectiveness of increasing the units’

capacities for patient journey optimization, we in-

creased the capacity by the same percentage for all

the medical units. According to Figure 5, it can be

observed that when all the resource capacities are in-

creased incrementally (10%, 20%, 30%), the reduc-

tion on average length of patient journey will then

drop accordingly. In fact, such drop could be at-

tributed to the fact that when the resource capaci-

ties are increased, patients would then be scheduled

with less idle times between treatment operations; and

hence with less chance to exchange timeslots with

others.

PATIENT JOURNEY OPTIMIZATION USING A MULTI-AGENT APPROACH

185

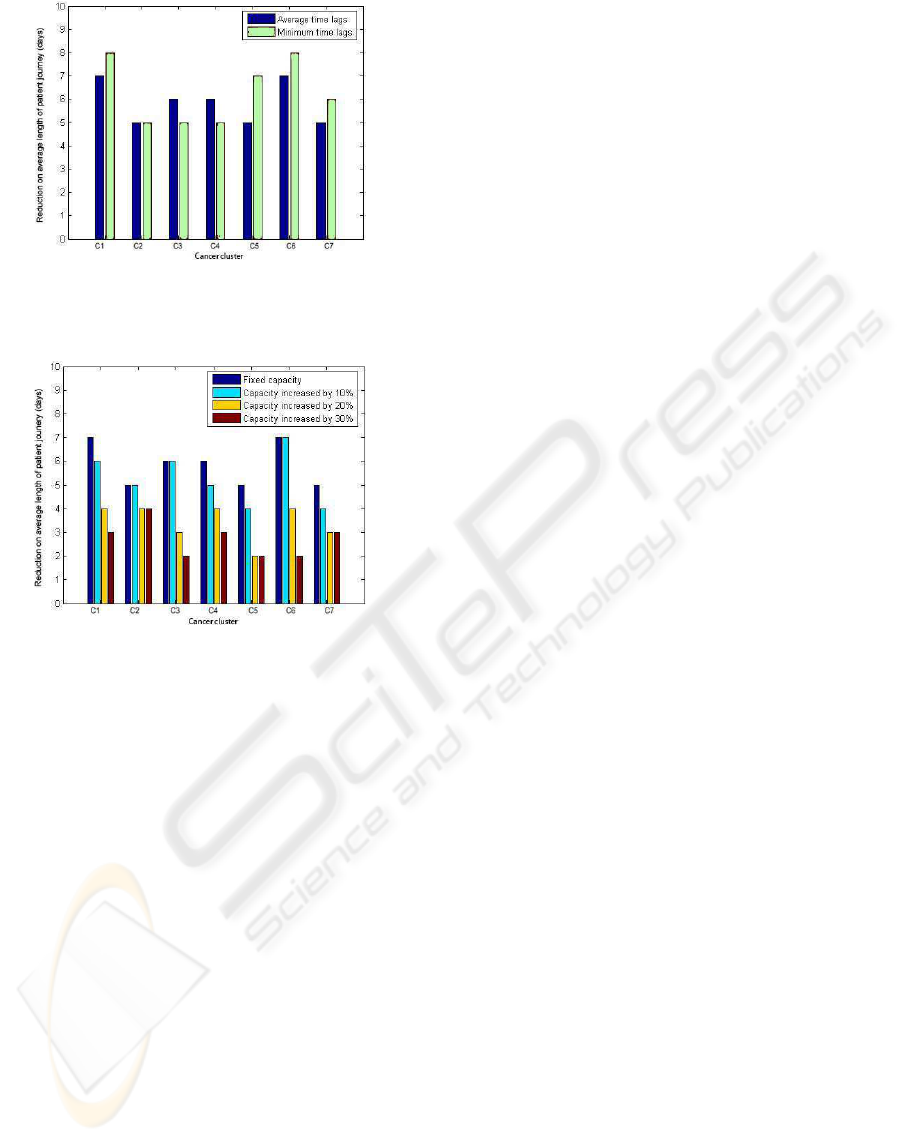
Figure 4: Reduction on average length of patient journey

(Setting 4) by varying the time lags between treatment op-

erations.

Figure 5: Reduction on average length of patient journey

(Setting 4) by varying capacities.

6 CONCLUSIONS

In this paper, a multi-agent approach was proposed

for patient journey optimization. Particularly, by ap-

plying the approach, the shortening of a patient jour-

ney will not lengthen the journeys of the others. Also,

all the temporal constraints among the treatment op-

erations for each patient would not be violated during

the scheduling process.

The effectiveness of the proposed approach has

been demonstrated by applying it to a dataset contain-

ing 5819 scheduled treatment plans of cancer patients

in Hong Kong. The effects of varying the initial as-

signment and the unit capacity on the overall reduc-

tion in length of patient journey are also studied.

Currently, since we are using a Pareto improve-

ment approach, it is assumed that no single patient

(agent) would get a lengthened schedule after swap-

ping timeslots with another. In the future, we are go-

ing to see whether there would be a greater improve-

ment in achieving a reduced average length of patient

journey when the above assumption for individuals is

relaxed.

ACKNOWLEDGEMENTS

This is to acknowledge Hospital Authority in Hong

Kong for providing the dataset to support this study.

REFERENCES

Czap, H. and Becker, M. (2003). Multi-agent systems

and microeconomic theory: A negotiation approach

to solve scheduling problems in high dynamic envi-

ronments. In HICSS ’03: Proceedings of the 36th An-

nual Hawaii International Conference on System Sci-

ences (HICSS’03) - Track 3, page 83.2, Washington,

DC, USA. IEEE Computer Society.

Decker, K., Li, J., and Demazeau, Y. (2000). Coordinating

mutually exclusive resources using gpgp. Autonomous

Agents and Multi-Agent Systems, 3:200–0.

Mao, X., Mors, A., Roos, N., and Witteveen, C. (2007).

Coordinating competitive agents in dynamic airport

resource scheduling. In MATES ’07: Proceedings

of the 5th German conference on Multiagent Sys-

tem Technologies, pages 133–144, Berlin, Heidelberg.

Springer-Verlag.

Patrick, J. and Puterman, M. (2008). Reducing wait times

through operations research: optimizing the use of

surge capacity. Healthc Q, 11(3):77–83.

Paulussen, T. O., Dept, I. S., Decker, K. S., Heinzl, A., and

Jennings, N. R. (2003). Distributed patient scheduling

in hospitals. In Coordination and Agent Technology

in Value Networks. GITO, pages 1224–1232. Morgan

Kaufmann.

Robu, V., Noot, H., La Poutr´e, H., and van Schijndel, W.-J.

(2008). An interactive platform for auction-based al-

location of loads in transportation logistics. In AAMAS

’08: Proceedings of the 7th international joint confer-

ence on Autonomous agents and multiagent systems,

pages 3–10, Richland, SC. International Foundation

for Autonomous Agents and Multiagent Systems.

Vermeulen, I., Bohte, S., Somefun, K., and La Poutre, H.

(2006). Improving patient activity schedules by multi-

agent pareto appointment exchanging. In CEC-EEE

’06: Proceedings of the The 8th IEEE International

Conference on E-Commerce Technology and The 3rd

IEEE International Conference on Enterprise Com-

puting, E-Commerce, and E-Services, page 9, Wash-

ington, DC, USA. IEEE Computer Society.

Vissers, J., Bekkers, J., and Adan, I. (2005). Patient mix op-

timization in tactical cardiothoracic surgery planning:

a case study. IMA Journal of Management Mathemat-

ics, 16.

Wang, M., Liu, J., Wang, H., Cheung, W. K., and Xie, X.

(2008). On-demand e-supply chain integration: A

multi-agent constraint-based approach. Expert Sys-

tems with Applications, 34(4):2683 – 2692.

HEALTHINF 2010 - International Conference on Health Informatics

186