FINGERPRINT IDENTIFICATION

A Support Vector Machine Approach

Terje Kristensen

Departement of Computer Engineering, Bergen University College

Nygårdsgaten 112, N-5020 Bergen, Norway

Keywords: AFIS, SVM, Classification rate.

Abstract: In this work a hybrid technique for classification of fingerprint identification has been developed to decrease

the matching time. For classification a Support Vector Machine is described and used. Automatic

Fingerprint Identification Systems are widely used today, and it is therefore necessary to find a

classification system that is less time-consuming. The given fingerprint database is decomposed into four

different subclasses and a SVM algorithm is used to train the system to do correct classification. The

classification rate has been estimated to about 87.0 % of unseen fingerprints. The average matching time is

decreased with a factor of about 3.5 compared to brute force search applied.

1 INTRODUCTION

Fingerprints have been used for identification for

hundreds of years. The first years, the matching of

fingerprints was done by human experts. 40 years

ago, researchers started to load digital fingerprint

data onto computers. The first Automatic Fingerprint

Identification System (AFIS) was developed in

1991, and since then, there has been an enormous

progress in the field. Due to the ever-growing

capabilities of computers and great achievements in

research, the recognition rate has improved

significantly. There is nevertheless a huge amount of

work to be done.

The current work in this field concentrates on

reducing the computation time for feature extraction

and matching. Embedded fingerprint systems

supporting instant identification or verification are

increasingly used, and the computation time for

these processes is thus an important research field.

One way to decrease this time is to divide the

fingerprint database into different subclasses based

on specific properties, such that only a part of the

fingerprints needs to be considered for matching.

The uniqueness of fingerprints has been widely

tested, and two identical fingerprints have still not

been found (Pankanti et al., 2002). However, current

finger print identification systems do not uses all the

discriminating information present in a fingerprint,

and the probability of finding two identical

fingerprints using the systems therefore increases. A

lot of work is being done today to decide which

information in fingerprints should be used to keep

the uniqueness. In addition to this work, the current

work in this field concentrates on reducing the

computation time for feature extraction and

matching.

Various methods have been used for

classification, and some of the most successful ones

use artificial neural networks as a classifier. In this

paper, however, a Support Vector Machine has been

used for classification. The SVM network is given a

feature vector as input, based on computation of the

Poincare index. This method was first proposed by

Jain, Prabhakar and Hong (Jain et al., 1999).

Among all the biometric techniques fingerprint

identification is today the most widely used

biometric identification form. It has been used in

numerous applications. Everyone is supposed to

have a unique, immutable fingerprint. It is also the

one that is scoring highest overall compared to other

forms as iris, signature, voice, etc. In 2002

fingerprint based biometric systems had a market of

52.1 % (Maltoni et al., 2005).

The problem is to develop algorithms which are

robust to noise in the fingerprints and are able to

deliver accuracy in real time.

Fingerprint matching algorithms vary greatly in

terms of false positive and false negative errors.

They may also vary with respect to features such as

451

Kristensen T. (2010).

FINGERPRINT IDENTIFICATION - A Support Vector Machine Approach.

In Proceedings of the 2nd International Conference on Agents and Artiﬁcial Intelligence - Artiﬁcial Intelligence, pages 451-458

DOI: 10.5220/0002694104510458

 SciTePress

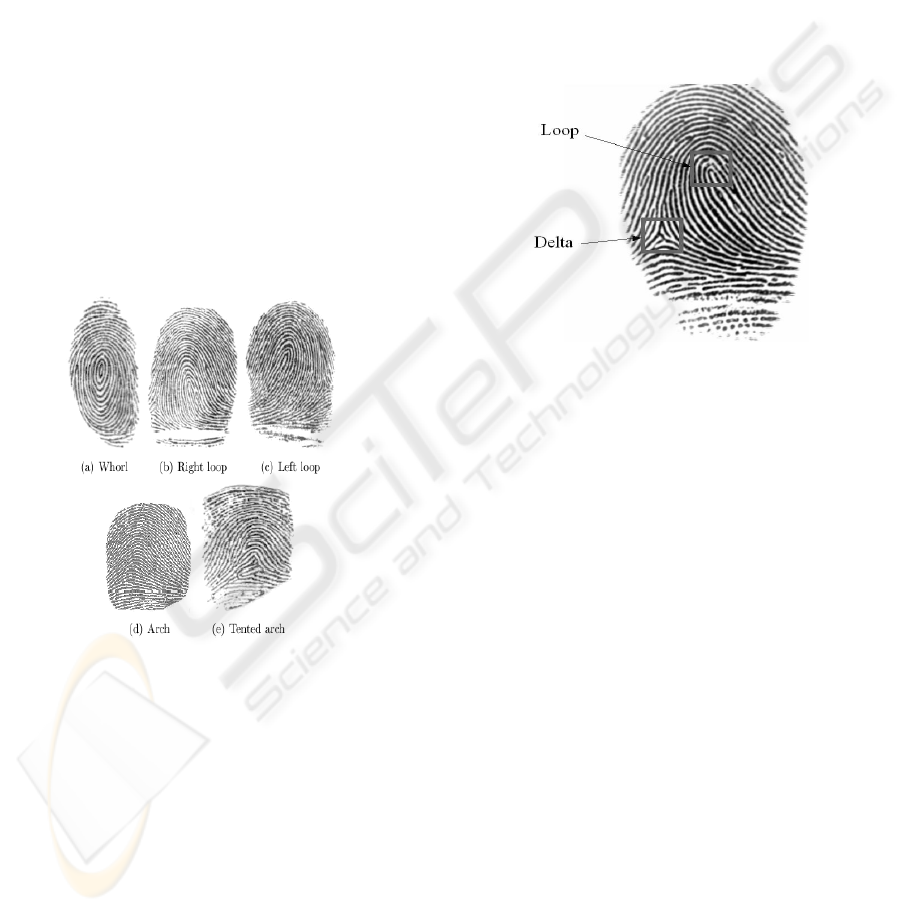
image rotation invariance and independence from a

reference point, given as the centre or the core of the

fingerprint pattern.

2 BACKGROUND

In an automatic fingerprint identification system

(AFIS), the fingerprint database can be huge, often

tens of thousands of fingerprints. If you were

supposed to check for similarity between the query

fingerprint and every other fingerprint in the

database, it would take an enormous amount of time.

With this in mind, fingerprint classification is an

important step that has to be implemented in every

fingerprint identification system. The classification

criteria most widely used are the modification or

extension of the standard Galton-Henrys

classification system (Henry, 1990). Here,

fingerprints are divided into 5 subclasses: whorl

(W), right loop (RL), left loop (LL), arch (A) and

tented arch (TA).

Figure 1: Five major fingerprint classes.

2.1 Singularities

Three singularities can be found in the fingerprint to

more easily distinguish between the classes. These

three singularities are the loop, the delta and the

whorl. A whorl fingerprint contains one or more

ridges that make a complete 360-degree path around

the centre of the fingerprint. Two loops (or one

whorl) and two deltas are present. The deltas are

placed under the whorl, one at the right and one at

the left side. A loop fingerprint has one or more

ridges that enter from one side, curves back and

exits at the same side as they entered. In a left and

right loop, the ridges enter from the left side and the

right side, respectively. A loop and a delta

singularity are present, with the delta under the loop,

at the left in a right loop fingerprint and at the right

in a left loop fingerprint. An arch fingerprint has

ridges that enter from one side, rises to a small bump

and exits at the opposite side.

When no singularities are present, this will make

the classification of the class rather difficult. A

tented arch fingerprint contains one or more ridges

that enter from one side, loops in a high curvature

and exit at the opposite site. When one loop and one

delta singularity are present, the delta is typically

placed right under the loop as shown in figure 2.

Figure 2: A loop and a delta singularity in a right loop

fingerprint.

It is possible to further subdivide each class into

more subclasses, but this is hardly of any practical

importance. In poor quality fingerprints it is really

difficult to even classify it to the five main classes,

and further classification would probably increase

the rejection rate. In addition, the complexity in the

end renders the classification incapable of improving

the identification time anymore.

2.2 Different Methods

Many fingerprint classification methods have been

proposed in literature. In general, these methods can

be categorised into five approaches (Maltoni, et al.,

2005):

• rule-based

• syntactic-based

• structure-based

• statistical-based

• neural-network based

In this work we have concentrated on the statistical-

based approach and want to see how the

performance of an AFIS comes out, based on SVM

as a classifier.

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

452

The current work in this field concentrates on

reducing the computation time for feature extraction

and matching. Embedded fingerprint systems

supporting instant identification or verification are

increasingly used, and the computation time for

these processes is thus an important research field.

One way to decrease this time is to divide the

fingerprint database into different subclasses based

on specific properties, such that only a part of the

fingerprints needs to be considered for matching.

3 EXTRACTING FEATURES

3.1 Extracting Classification Features

The SVM network needs an input vector to be able

to classify the fingerprints. This vector can be made

by extracting features of the fingerprint, and then

represent these features in a suitable way. We have

chosen to create this vector based on a technique

proposed by (Maltoni et al., 2005). Here, the authors

present a feature vector called FingerCode, which is

a vector consisting of 640 feature values.

First, a reference point in the fingerprint is to be

found. We set the core of the fingerprint as the

reference point. Then, the image is filtered in eight

different directions using different Gabor filters,

each enhancing ridges oriented in different angles.

Each of these eight images are divided into 80

sectors according to specific rules. The standard

deviation of each sector is finally calculated, and

these values represent the feature values. The total

number of feature values is 640 (8 x 80), and a

vector containing these values is used as input vector

to the SVM network.

3.2 Reference Point Detection

We have chosen to use the core point as the

reference point. This core point is defined as the

most northern loop singularity in a fingerprint. A

loop singularity can be detected by a method based

on the Poincare index proposed in (Jain et al., 1999).

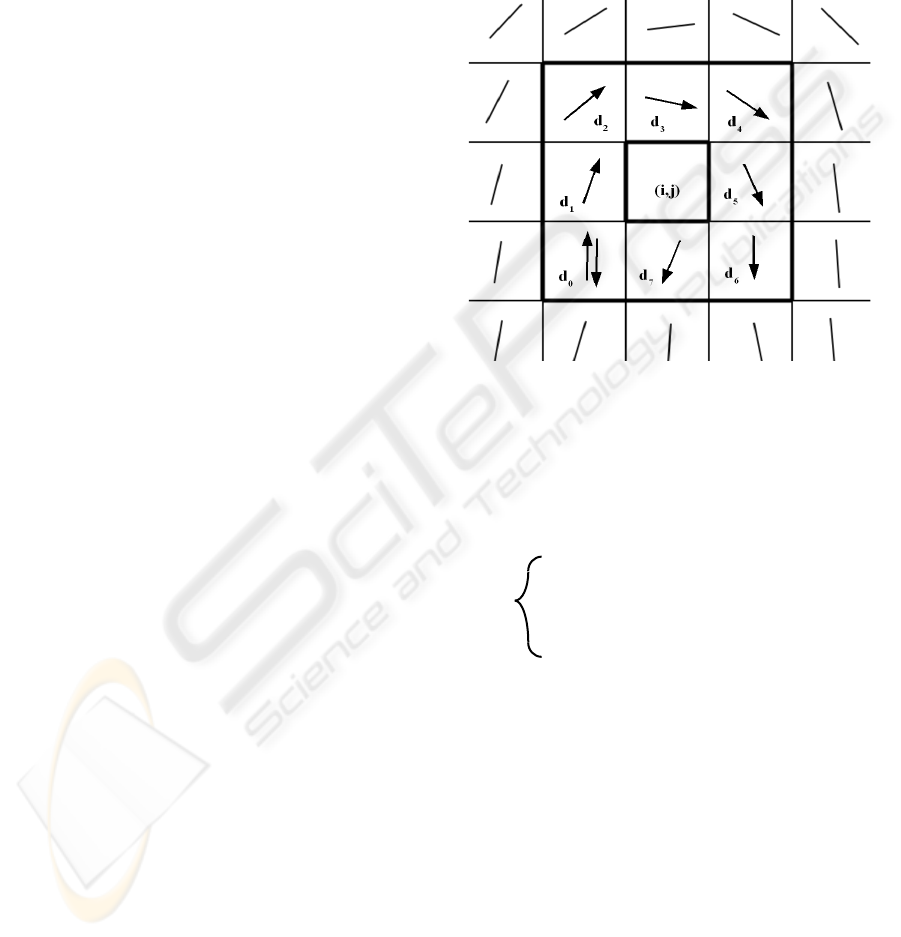
Let G be a vector field and C be a curve immersed

in G. Then, the Poincare index is defined as the total

rotation of the vectors of G along C. Here, G is the

vector field associated with an orientation image of

the fingerprint. The curve C is a closed path defined

as an ordered sequence of the neighbour elements d

of position (i,j) in the orientation image. Then, the

Poincare index at position (i,j) is defined as the sum

of the orientation differences between adjacent

elements of C:

G,C =

(1)mod8)

(,( )kk

angle d d +

∑

(1)

where d

k is the neighbouring elements as shown in

Figure 3. This figure shows a typical loop

singularity, and the sum of angles will here be 180

degrees. Because the left neighbour of d

7 is d0,

d((k+1) mod 8) is used instead of dk+1.

Figure 3: Computation of the Poincare index in the eight-

neighbourhood of pixel (i, j).

It is shown that the sum of Poincare indexes must be

either -360, -180, 0, 180 or 360. These indexes

thereby give a clear indication of which singular

region (SR) a pixel (i,j) belongs to, see (Kawagoe,

Tojo, 1984):

0 deg. if (i,j) does not belong to any SR

360 deg. if (i,j) belongs to a whorl type SR

180 deg. if (i,j) belongs to a loop type SR

-180 deg. if (i,j) belongs to a delta type SR

(2)

As mentioned, the core point is the northern most

loop. We assume that the fingerprints are captured

with the finger in an approximately normal position,

but tolerate a rotation of up to 45 degrees either

clockwise or counter clockwise. The core point is

used as reference point in the extraction of

classification features.

3.3 Gabor Filtering

After the reference point is detected, the image is

filtered using eight different Gabor filters. The

image needs to be divided into 80 sectors, as

illustrated in Figure 4. Here, the reference point is

marked with a cross. Note that the innermost band is

not divided into sectors, as it contains very few

G,C

FINGERPRINT IDENTIFICATION - A Support Vector Machine Approach

453

pixels, and the standard deviation will then become

very unreliable. Before filtering, each of the 80

sectors has to be normalized, setting the mean and

variance to desired values.

Figure 4: Computation of the Poincare index in the eight-

neighbourhood of pixel (i, j).

Each sector is normalized locally, so the mean and

variance have to be calculated for each sector. The

desired mean and variance value for each sector are

both set to 100, as recommended by the authors in

(Delima, Yen, 2003).

Let I(i, j) denote the gray level at pixel (i, j) in a

fingerprint image of size m x n and let (i

) denote

the reference point or core point. The region of

interest is defined by a collection of sectors Sp,

where the sector Sp is computed in terms of

parameters (r,θ) defined by (Burges, 1998):

Sp = {i,j)|b(T

+ 1)

≤

r ≤ b(T

+2)}

1 ≤i ≤ n, 1≤j≤m,

≤ θ < θ

(3)

where

Tp = p div k,

(4)

= (p mod k)(

2Π

/k)

(5)

r =

2 2

()( )ccii j j−+−

(6)

θ = tan

-1

((j-j

)/(i - i

))

(7)

b is the width of each band and k is the number of

sectors considered in each band. The Gabor filters

use eight fixed angle values; θ ε {0 degrees, 22.5

degrees, 45 degrees, . . . , 157.5 degrees}. The

frequency is fixed, to limit computation, and set as

the average ridge frequency in the region of interest.

The region of interest is here the union of all the

sectors defined above. The Gabor filtering results in

eight images that each enhance the ridges in a

specific direction and also remove noise, thereby

emphasising the relevant information.

3.4 The Feature Vector

The feature vector is, as earlier mentioned, a vector

consisting of 80 values for each of the eight Gabor

filtered images. In each of these images, a section of

the fingerprint containing ridges that are parallel to

the corresponding filter direction, exhibits a higher

variation. A section containing ridges that are not

parallel to the corresponding filter tends to be

smoothed by the filter, which results in a lower

variation. The spatial distribution of the variations in

the different sectors of the component images can

thereby be a good characterisation of the global

ridge structure. With this in mind, the feature vector

is defined as a vector containing the standard

deviation of all 80 sectors in the filtered image for

all angles θ [8].

Let F

pθ

(i,j) be the θ-direction filtered image for

section Sp. For p ε { 0,1,. . . ,79} and θ ε {0

degrees, 22.5 degrees, . . , 157.5 degrees}, the

feature value is the standard deviation Vp

, defined

as:

pθ

((,) )

ij P

θθ

−

∑

(8)

where K

p is the number of pixels in Sp and Ppθ is the

mean value of pixels in S

p in image Fpθ (i, j). Now,

we have a 640- dimensional feature vector that can

be used as input vector to the SVM network.

3.5 Scaling

To improve the classification rate, all feature vectors

are scaled before training. The main advantage of

scaling is to avoid attributes with big values which

dominate those with small values.

Another advantage is to avoid numerical

difficulties during the calculation. Because the

kernel values in a Support Vector Machines depend

on the inner products of the feature vectors, large

attribute values may cause numerical problems.

Scaling also makes the training run faster, and

decreases the chance of getting stuck in local

optima. The feature vectors are linearly scaled to the

range [-1, +1]. Each value j in a feature vector i is

scaled individually:

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

454

i,j

= -1 + 2*

(, ) min

max min

Vij i

−

(9)

where FV(i,j) and S

i,j are the feature value and scaled

feature value at position j for feature vector i,

respectively.

min j and max j are the minimum and

maximum feature value at position

j for all feature

vectors, respectively. The table must appear inside

the designated margins or it may span the two

columns.

4 SUPPORT VECTOR

MACHINES

Support Vector Machines is a computationally

efficient learning technique that is now being widely

used in pattern recognition and classification

problems (Burges, 1998). This approach has been

derived from some of the ideas of the statistical

learning theory regarding controlling the

generalization abilities of a learning machine

(Vapnik, 1998, Vapnik, 1999).

In this approach the machine learns an optimum

hyper plane that classifies the given pattern. By use

of kernel functions, the input feature space by

applications of a non-linear function can be

transformed into a higher dimensional space where

the optimum hyper plane can be learnt. This gives a

flexibility of using one of many learning models by

changing the kernel functions.

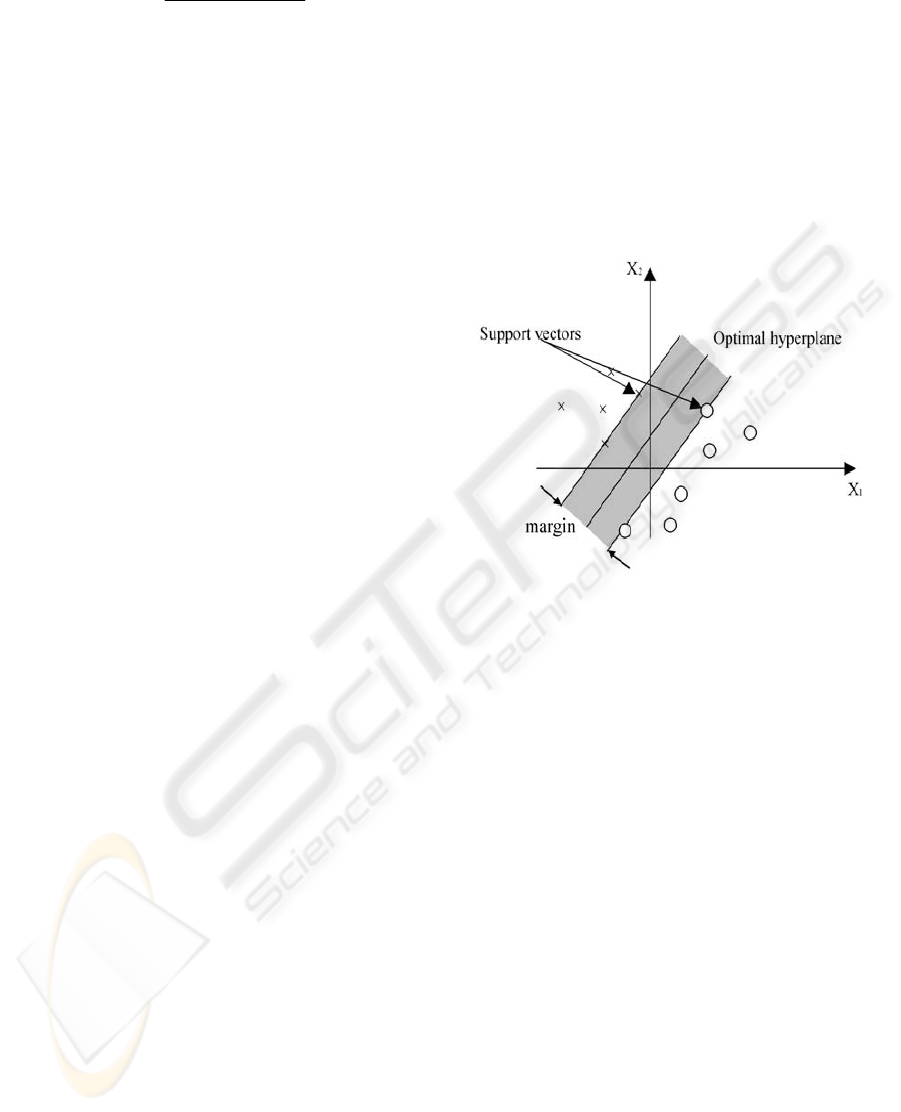
4.1 The SVM Classifier

The basic idea of an SVM classifier is illustrated in

Figure 5. This figure shows the simplest case in

which the data vectors (marked by 'X' s and 'O' s)

can be separated by a hyper plane. In such a case

there may exist many separating hyper planes.

Among them, the SVM classifier seeks the

separating hyper plane that produces the largest

separation margin.

In the more general case in which the data points

are not linearly separable in the input space, a non-

linear transformation is used to map the data vectors

into a high-dimensional space (called feature space)

prior to applying the linear maximum margin

classifier. To avoid the potential pitfall of over-

fitting in this higher dimensional space, an SVM

uses a kernel function in which the non-linear

mapping is implicitly embedded. A function

qualifies as a kernel function if it satisfies the

Mercer's condition (Vapnik, 1998).

With the use of a kernel function, the

discriminant function in an SVM classifier has the

following form

f(x) =

∑

K(x

x) + α

(10)

where K(-,-) is the kernel function, x

are the support

vectors determined from the training data, y

is the

class indicator e.g. +1 and -1 for a two class problem

associated with each x

, N

is the number of

supporting vectors

determined during training.

Figure 5: A support vector machine classification defined

by a linear hyper plane that maximizes the separating

margins between the classes.

Support vectors are elements of the training set

that lie either exactly on or inside the decision

boundaries of the classifier. In essence, they consist

of those training examples that are most difficult to

classify. The SVM classifier uses these borderline

examples to define its decision boundary between

the two classes.

4.2 SVM Kernel Functions

The kernel function plays a central role of implicitly

mapping the input vectors into a high dimensional

feature space, in which linear separability is

achieved. The most commonly used kernel functions

are the polynomial kernel given by :

K(x,y) = (

y + 1)

(11)

where p > 0 is a constant, and the Gaussian radial

basis function (RBF) kernel given by

x,y) = exp ( -||x-y||/2σ

)

(12)

where σ > 0 is a constant that defines the kernel

width. Both of these kernels satisfy the Mercer

condition mentioned earlier.

FINGERPRINT IDENTIFICATION - A Support Vector Machine Approach

455

4.3 SVM Training

The fingerprints are classified by a Support Vector

Machine (SVM). The feature vector created is used

as an input pattern to the classifier. The SVM

network needs to be trained well to be able to

classify unknown patterns correctly.

We have manually labelled the fingerprint

images according to the Henry classification to

create a training set. Each classifier is trained using

the feature vector extracted from these labelled

images. The SVM classifier has been tested by

presenting it to an unknown set of fingerprints to see

how SVM is able to classify unknown patterns

correctly. Fingerprint images with no core point or a

core point too lose to an edge or segmented area is

not used for training, due to false feature values. If

such an image occurs in the classification stage, the

images cannot be classified and must be matched

against every other fingerprint in the final matching

stage.

5 EXPERIMENTS AND RESULTS

A Support Vector Machine is trained according to

the numbers specified in Table 1. Arch images have

no singularities present, and a reference point of

these fingerprints are thereby not possible by our

methods. However, loops constitute about 65

percent of the total fingerprint patterns, whorls about

30 percent, and arches and tented arches together

account for the other 5 percent (Karu, Jain, 1996).

This makes the problem of not being able to classify

arches less important.

Table 1: The number of training and testing instances for

each fingerprint.

Training Testing

LL 127 63

RL 123 59

TA 10 6

W 83 41

Total 343 169

We have used the LIBSVM library for SVM-

classification (Chang, Lin, 2001). The SVM is

trained using a Radial Basis Function kernel, as

given in equation 13.

K(x

, x

) = e

||xi - xj||

, γ > 0

(13)

Before training, the parameters C and γ

above have

to be set to correct values.

C is the penalty

parameter of the error term and γ is a kernel

parameter. By cross-validation, the best C- and γ-

values are found to be 8.0 and 0.001953125,

respectively. We have used a one-vs-one approach to

a multi-class problem. This splits our classification

problem into six separate problems, that in the end

are combined into one final set of support vectors. In

total, this set, which is used for classification of the

unknown fingerprints, contains 232 support vectors.

The classification results using SVM as a classifier

are shown in Table 2.

Table 2: Classification results of each class using a SVM

network.

True

Classes

Produced

Classes

LL RL TA W

LL 59 1 0 3

RL 1 55 0 3

TA 2 2 2 0

W 6 4 0 31

Best 96.8 97.6 98.1

From table 3 we see that the SVM classifier is able

to classify the loops very well (93.7% and 93.2%),

but is not able to classify the whorls and tented

arches at the same rate.

A benchmark test was carried out on the whole

set of fingerprints available to measure the average

matching time of a fingerprint query by using a brute

force search through the whole finger database

compared to a regime with a classification stage.

The benchmark test showed that the matching time

was reduced with a factor of about 3.5 by

introducing a classification in the AFIS regime.

Table 3: Classification rate for each class using a SVM

network.

Correct Wrong Percent Correct

LL 59 4 93.7

RL 55 4 93.2

TA 2 4 33.3

W 31 10 75.6

Total 147 22 87.0

6 DISCUSSION

The performance rate of the SVM network has been

estimated to about 87.0%. The SVM classifier

failed in classifying most of the tented arch

fingerprints, but this is because we believe there are

too few training instances belonging to the tented

arch class. SVM also performed better in

classification of left loops and right loops than

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

456

classification of whorls. We believe that this is

caused by the limited region-of-interest used to

calculate the feature vector, causing many whorls to

be wrongly classified as loops.

There are two main classes of whorls, classic

whorl and double loop, and the double loop causes

the classification problem. This is because the

region-of interest centred in the core looks quite

similar in double loops and normal loops. Thereby,

they can easily be misclassified as loops. A solution

could be to increase the region-of-interest, but this

would also increase the rejection rate, as more

sectors would be outside the fingerprint area or even

outside the entire image.

The experiments have shown that a SVM

network is able to do a correct classification with a

rate of about 87.0% on a four-class classification

problem. To see how well such a classification rate

is, it is compared with results obtained from

literature. In [10], a classification algorithm based on

the number of cores and deltas, and their relative

positions, is presented. The authors achieved a

correct classification rate of 85.4% on a five-class

classification task.

In (Cappelli et al., 1999) one partitioned the

directional image into connected regions according

to the fingerprint topology, thus giving a synthetic

representation which can be exploited as a basis for

the classification. This method achieved a correct

classification rate of 92.1% on a five-class

classification task.

The authors in (Jain et al., 1999) used an

approach similar to the one used in this paper, with

the FingerCode as feature vector. The classification

was done by a Multi Layered Perceptron (MLP)

neural network. The network was able to achieve a

correct classification rate of 86.4% on a five-class

classification task and 92.1% on a four class

classification problem.

In this paper a SVM network has been used in

the classification stage. We observe that using a

SVM network as a classifier gives nearly similar

results as those found in the literature. From our

experience with SVM network we believe that a

larger database than was available would probably

increase the performance rate, since a SVM network

is capable to handle higher dimensional input spaces

often in a better way than a MLP network and also

generalize better. Such a classifier will then be more

able to distinguish between more subtle differences

of the fingerprint classes.

A benchmark test of a trained SVM network has

been carried out on the total set of fingerprints to

measure the average matching time of a query

fingerprint compared to the query fingerprint using a

subclass regime. The matching time of the last

regime was also reduced by the factor of 3.5

compared to the brute force search regime.

7 CONCLUSIONS

One way to decrease the identification time of an

AFIS is to divide a finger database into different

subclasses so that that a query fingerprint does not

have to be tested against every fingerprint in the

database. To solve such a problem we have

implemented a classification stage in the AFIS by

using a SVM classifier.

The SVM classifier is able to classify different

unseen fingerprints with a performance rate of

approximately 87.0%. However, by using a

classification stage one is also able to reduce the

average matching time compared to a total search

which may be important when the fingerprint

database is becoming huge.

However, the main objection by the method used

in this paper is that the number of training examples

are too small compared to the number of features in

the FingerCode vector. By training the SVM with an

extended training database we believe that the

performance rate will greatly improve. Other types

of neural networks may also be used to do the

classification instead of the SVM network. This

belongs to our future research.

REFERENCES

Burges, C.J., 1998. A Tutorial on Support vector

Machines for Pattern Recognition. The book

Knowledge Discovery and Data Mining 2.

Cappelli, R., Lumini, A., Maio, D., Maltoni, D., 1999.

Fingerprint Classification by Directional Image

Partitioning In IEEE Trans. Pattern Anal. Mach.

Intell., vol. 21, nr.5, pp.402-421. IEEE Computer

Society.

Chang, C.C., Lin,C.J., 2001. The book LIBSVM : a

library for Support Vector Machines. Software

available online at http://www.csie.ntu.edu.tw/

cjlin/libsvm.

DeLima, P.G., Yen, G.G., 2003. Multiple model fault

tolerant control using globalized dual heuristic

programming. In IEEE Proceedings International

Symposium on Intelligent Control, Houston, TX, pp.

523–528.

Henry, E.R., 1990. Classification and Uses of Finger

prints, The book Pattern Recognition, George

Routledge and sons: London.

FINGERPRINT IDENTIFICATION - A Support Vector Machine Approach

457

Jain, A.K., Prabhakar, S., Hong, L., 1999. A Multichannel

Approach to Fingerprint Classification. In IEEE

Transactions on Pattern Analysis and Machine

Intelligence, vol. 21, pp. 348–359.

Jain, A.K., Farrokhnia,F., 1999. Unsupervised texture

segmentation using Gabor filters, The book Pattern

Recognition, vol. 24, nr. 12, pp.1167-1186. Elsevier

Science Inc.

Jain, A.K., Prabhakar, S., Hong, L., Pankanti, S., 1999.

FingerCode: A Filterbank for Fingerprint

Representation and Matching. In Proc. IEEE

Conference on CVPR, Colorado vol.2, pp. 187-195

Kawagoe, M., Tojo A., 1984. Fingerprint pattern

classification. In the book Pattern Recognition, vol.

17(3), pp. 295-303.

Karu, K., Jain, A.K., 1996. Fingerprint Classification. The

book Pattern Recognition, vol.29, nr. 3, pp. 389-404.

Maltoni,D. Maio,D, Jain,A.J., Prabhakar,S., 2005. The

handbook of Fingerprint Recognition, Springer.

Pankanti,S., Prabhakar,S., Jain A., 2002 On the

Individuality of fingerprints. In IEEE Transactions on

Pattern Analysis and Machine Intelligence, 24 (8), pp.

1010-1025.

VapnikV.N., 1999. An overview of statistical learning

theory. In IEEE transactions on Neural Networks, 10

sept.

Vapnik,V.N., 1998. The book Statistical Learning Theory,

Wiley, New York.

ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence

458